1.1.5 堆Heap
1.1.5 堆Heap
import heapq
实现最小堆:
- heap = [] #创建了一个空堆
- heapq.heappush ( heap,item ) #往堆heap中插入一条新的值item
- heapq.heapify(listx) #以线性时间将一个列表转化成堆
- item = heapq.heappop ( heap ) # 从堆中弹出最小值
- item = heap [0] #查看堆中最小值,不弹出
- item = heapq.heapreplace(heap,item) #弹出并返回最小值,然后将heapreplace方法中item的值插入到堆中,堆的整体结构不会发生改变。这里需要考虑到的情况就是如果弹出的值大于item的时候我们可能就需要添加条件来满足function的要求:
- if item > heap[0]: item = heapreplace(heap, item)
- heapq.heappushpop() #顾名思义,将值插入到堆中同时弹出堆中的最小值。
- merge(heap1,heap2,heap3) #合并多个堆然后输出
- heapq.nlargest(n , heap, key=None) #从堆中找出做大的N个数,key的作用和sorted( )方法里面的key类似,用列表元素的某个属性和函数作为关键字。
- heapq.nsmallest(n, iterable, key=None) #找到堆中最小的N个数用法同上。
实现最大堆:将元素取反存入堆,取出时再取反:将push(e)改为push(-e)、pop(e)改为-pop(e)。
堆(heap)
又被为优先队列(priority queue)。尽管名为优先队列,但堆并不是队列。回忆一下,在队列中,我们可以进行的限定操作是dequeue和enqueue。
dequeue是按照进入队列的先后顺序来取出元素。而在堆中,我们不是按照元素进入队列的先后顺序取出元素的,而是按照元素的优先级取出元素。
性质
堆的实现通过构造二叉堆(binary heap),实为二叉树的一种;由于其应用的普遍性,当不加限定时,均指该数据结构的这种实现。这种数据结构具有以下性质。
- 任意节点小于(或大于)它的所有后裔,最小元(或最大元)在堆的根上(堆序性)。
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
实现
- 堆的主要操作是插入和删除最小元素(元素值本身为优先级键值,小元素享有高优先级)
- 在插入或者删除操作之后,我们必须保持该实现应有的性质: 1. 完全二叉树 2. 每个节点值都小于或等于它的子节点
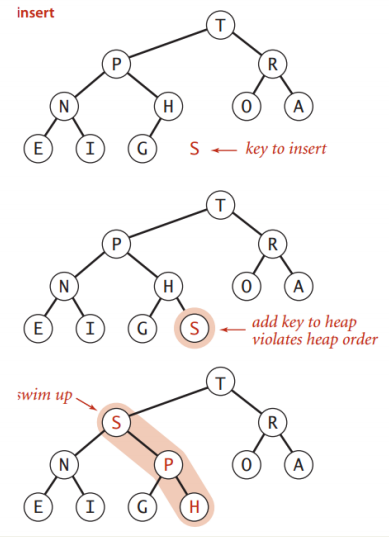
上浮(Promotion)
情境: 子节点的键值变为比父节点的键值大;如下面添加字节点
消除这种违反项:
- 交换子节点的键和父节点的键
- 重复这个过程直到堆的顺序恢复正常
堆的添加:
def _upheap(self, j):#往上交换
parent = self._parent(j)
if j > 0 and self._data[j] < self._data[parent]:
self._swap(j, parent)
self._upheap(parent)
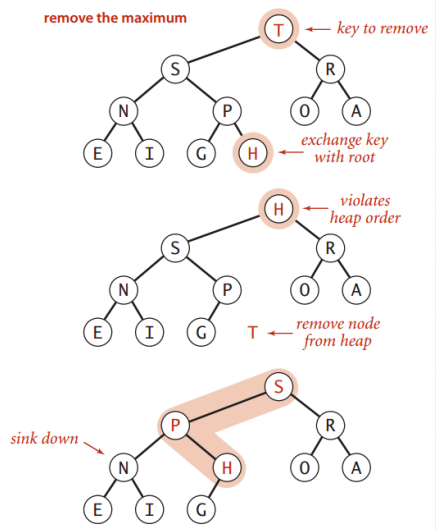
下沉(Demotion)
情境:父节点的键值变得比子节点(一个或者2个) 的键值还小 ,如下面删除了根节点后拿了个小子节点补充上来的情况
消除这种违反项:
- 把父节点的键值和比它大的子节点的键值做交换
- 重复这个操作直到堆的顺序恢复正常
删除最大值
def _downheap(self, j):#往下交换,递归比较三个值
if self._has_left(j):
left = self._left(j)
small_child = left
if self._has_right(j):
right = self._right(j)
if self._data[right] < self._data[left]:
small_child = right
if self._data[small_child] < self._data[j]:
self._swap(j, small_child)
self._downheap(small_child)
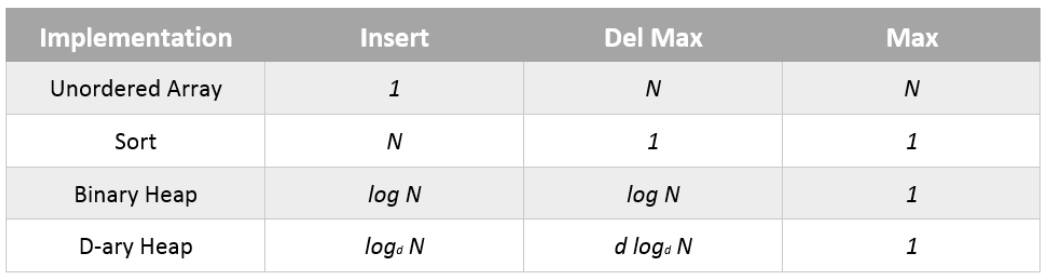
复杂度分析
构建堆的代码:
#该heap为min_heap,即根节点为最小值
class PriorityQueueBase:
#抽象基类为堆
class Item:
#轻量级组合来存储堆项目
__slots__ = '_key' , '_value'
def __init__ (self, k, v):
self._key = k
self._value = v
def __lt__ (self, other): #比较大小
return self._key < other._key
def is_empty(self):
return len(self) == 0
def __str__(self):
return str(self._key)
class HeapPriorityQueue(PriorityQueueBase):
def __init__ (self):
self._data = [ ]
def __len__ (self):
return len(self._data)
def is_empty(self):
return len(self) == 0
def add(self, key, value): #在后面加上然后加上
self._data.append(self.Item(key, value))
self._upheap(len(self._data) - 1)
def min(self):
if self.is_empty():
raise ValueError( "Priority queue is empty." )
item = self._data[0]
return (item._key, item._value)
def remove_min(self):
if self.is_empty():
raise ValueError( "Priority queue is empty." )
self._swap(0, len(self._data) - 1)
item = self._data.pop( )
self._downheap(0)
return (item._key, item._value)
def _parent(self, j):
return (j - 1) // 2
def _left(self, j):
return 2 * j + 1
def _right(self, j):
return 2 * j + 2
def _has_left(self, j):
return self._left(j) < len(self._data)
def _has_right(self, j):
return self._right(j) < len(self._data)
def _swap(self, i, j):
self._data[i], self._data[j] = self._data[j], self._data[i]
def _upheap(self, j):#往上交换
parent = self._parent(j)
if j > 0 and self._data[j] < self._data[parent]:
self._swap(j, parent)
self._upheap(parent)
def _downheap(self, j):#往下交换,递归比较三个值
if self._has_left(j):
left = self._left(j)
small_child = left
if self._has_right(j):
right = self._right(j)
if self._data[right] < self._data[left]:
small_child = right
if self._data[small_child] < self._data[j]:
self._swap(j, small_child)
self._downheap(small_child)
python内置方法创建堆有两种方式,heappush()和heapify():
'''
heaqp模块提供了堆队列算法的实现,也称为优先级队列算法。
要创建堆,请使用初始化为[]的列表,或者可以通过函数heapify()将填充列表转换为堆。
提供以下功能:
heapq.heappush(堆,项目)
将值项推入堆中,保持堆不变。
heapq.heapify(x)
在线性时间内将列表x转换为堆。
heapq.heappop(堆)
弹出并返回堆中的最小项,保持堆不变。如果堆是空的,则引发IndexError。
'''
import heapq #1 heappush生成堆+ heappop把堆从小到大pop出来
heap = []
data = [1,3,5,7,9,2,4,6,8,0]
for i in data:
heapq.heappush(heap,i)
print(heap) lis = []
while heap:
lis.append(heapq.heappop(heap))
print(lis) #2 heapify生成堆+ heappop把堆从小到大pop出来
data2 = [1,5,3,2,9,5]
heapq.heapify(data2)
print(data2) lis2 = []
while data2:
lis2.append(heapq.heappop(data2))
print(lis2) #输出结果
[0, 1, 2, 6, 3, 5, 4, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 5, 9, 5]
[1, 2, 3, 5, 5, 9]
堆接口
我们将使用堆来实现一个优先队列,堆接口应该包含返回其大小、添加项、删除项和查看项的方法。
堆接口中的方法
- heap.isEmpty() 如果堆为空,返回True,否则,返回False
- heap.len() 等同于len(heap),返回堆中项的数目
- heap.iter() 等同于iter(heap)或for item in heap;从最小到最大地访问各项
- heap.str() 等同于str(heap),返回一个字符串,表示堆的形状
- heap.contains(item) 等同于item in heap。如果item在堆中,返回True
- heap.add(otherHeap) 等同于heap + otherHeap,返回一个新的堆,其内容是heap和otherHeap的内容
- heap.eq(anyObject) 等同于heap == otherObject,如果堆等于anyObject的话,返回True。如果两个堆包含相同的项,那么它们相等
- heap.peek() 返回heap最顶部的项。先验条件:heap不为空
- heap.add(item) 将item插入到其在heap中适当的位置
- heap.pop() 返回heap最顶部的项。先验条件:heap不为空
两个最为重要的堆操作是add和pop。add方法接收一个可比较的元素作为参数,并且将该元素插入到堆中合适的位置。这个位置通常位于一个比它大的元素之上的一层,并且位于一个比它小的元素之下。重复的元素会放置在之前输入的那个元素之下。pop方法删除堆中最顶端的元素,并返回最顶端的元素,并且维护堆的属性。peek操作返回堆最顶端的元素,但是不会删除它。
add方法(插入)和pop方法(删除)在整个堆实现都会使用,它们定义于ArrayHeap类中。在基于数组的实现中,这两个方法都需要在数组中维护堆的结构(实际上,使用了一个Python列表,但是在如下的讨论中,我们将这个结构称为一个数组)。
堆的实现
插入操作add
目标是在堆中找到新元素的合适位置,并且将其插入。下面是插入的策略:
(1)首先在堆的底部插入该元素,在数组实现中,这是数组中当前最后一个元素之后的位置
(2)然后,进入一个循环,只要新元素的值小于其父节点的值,循环就让这个新元素沿着堆向上“走”,将新的元素和其父节点交换。当这个过程停止的时候(要么新的元素大于或等于其父节点,要么到达了顶部的节点),新的元素就位于其适当的位置。
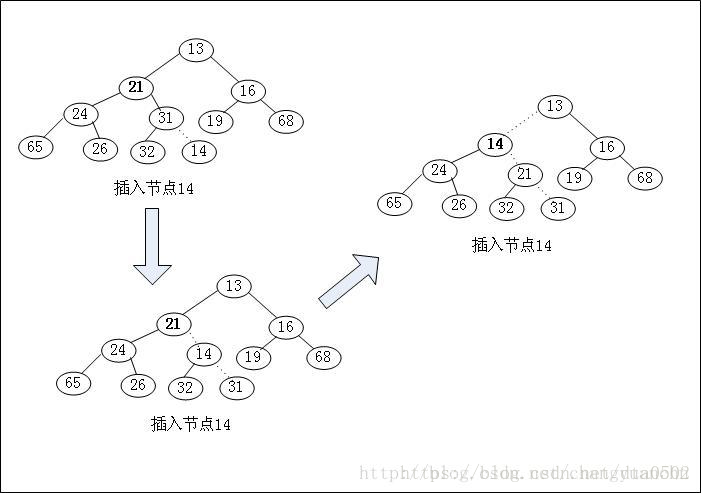
注意:数组一个元素的父节点的位置是通过将元素的位置减去1并且将结果除以2计算得到的。堆的最顶端在数组中的位置是0。
def add(self, item):
self._size += 1
self._heap.append(item)
curPos = len(self._heap) - 1
while curPos > 0:
parent = (curPos - 1) // 2
parentItem = self._heap[parent]
if parentItem <= item:
break
else:
self._heap[curPos] = self._heap[parent]
self._heap[parent] = item
curPos = parent
该方法的快速分析揭示了,你最多需要进行log2N次比较,就可以从底部移动至树的上面,因此,一次add操作是O(logN)。该方法偶尔会触发底层数组的大小翻倍,当发生翻倍的情况时,该操作就是O(n),但这是将所有的相加操作都累计到一起,而每次相加操作都是O(1)。
删除操作pop
删除的目标是在删除根节点之后,返回该节点中的元素,并且调整其他节点的位置以维护堆属性。下面是删除操作的策略:
(1)首先,保存堆中的顶部元素和底部元素的指针,并且将该元素从堆的底部移动到顶部
(2)从堆的顶部往下走,将最小的元素向上移动一层,直到到达堆的底部
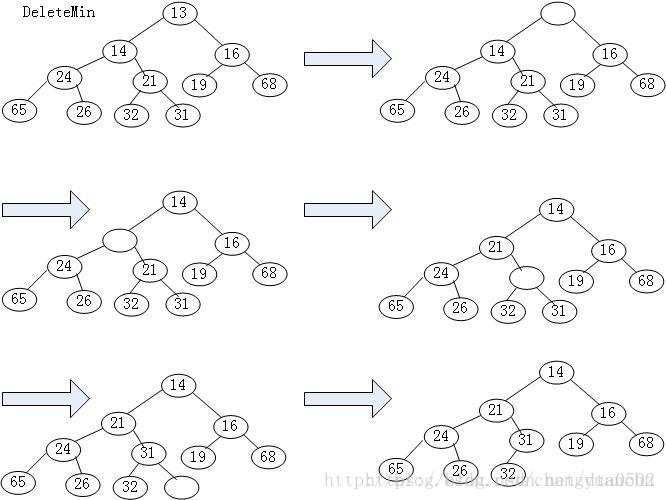
def pop(self):
if self.isEmpty():
raise Exception("Heap is empty")
self._size -= 1
topItem = self._heap[0]
bottomItem = self._heap.pop(len(self._heap) - 1)
if len(self._heap) == 0:
return bottomItem
self._heap[0] = bottomItem
lastIndex = len(self._heap) - 1
curPos = 0
while True:
leftChild = 2 * curPos + 1
rightChild = 2 * curPos + 2
if leftChild > lastIndex:
break
if rightChild > lastIndex:
maxChild = leftChild;
else:
leftItem = self._heap[leftChild]
rightItem = self._heap[rightChild]
if leftItem < rightItem:
maxChild = leftChild
else:
maxChild = rightChild
maxItem = self._heap[maxChild]
if bottomItem <= maxItem:
break
else:
self._heap[curPos] = self._heap[maxChild]
self._heap[maxChild] = bottomItem
curPos = maxChild
return topItem
二项堆[1]
在计算机科学中,二项堆(Binomial Heap)是一种堆结构。与二叉堆(Binary Heap)相比,其优势是可以快速合并两个堆,因此它属于可合并堆(Mergeable Heap)数据结构的一种。
可合并堆通常支持下面几种操作:
- Make-Heap():创建并返回一个不包含任何元素的新堆。
- Insert(H, x):将节点 x 插入到堆 H 中。
- Minimum(H):返回堆 H 中的最小关键字。
- Extract-Min(H):将堆 H 中包含最小关键字的节点删除。
- Union(H1, H2):创建并返回一个包含 H1和 H2 的新堆。
- Decrease-Key(H, x, k):将新关键字 k 赋给堆 H 中的节点 x。
- Delete(H, x):从堆 H 中删除 节点 x。
二项树
一个二项堆由一组二项树所构成,二项树是一种特殊的多分支有序树,如下图 (a)。
![img]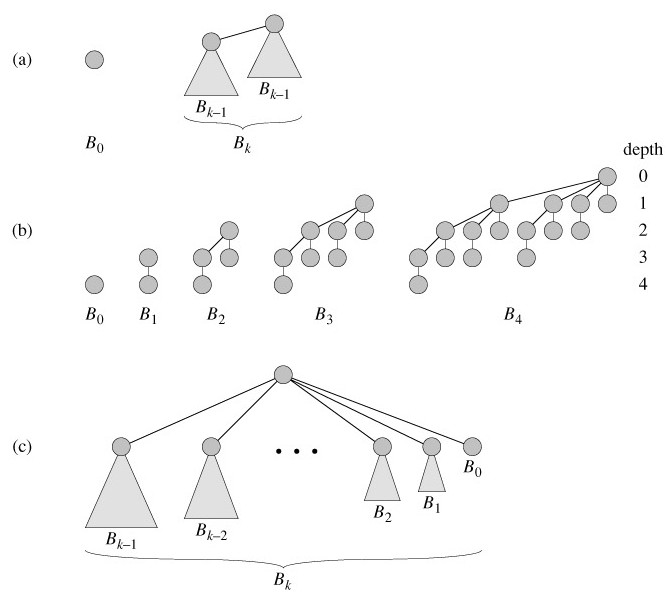
二项树 Bk 是一种递归定义的有序树。二项树 B0 只包含一个结点。二项树 Bk 由两个子树 Bk-1 连接而成:其中一棵树的根是另一棵树的根的最左孩子。
二项树的性质有:
- 共有 2k 个节点。
- 树的高度为 k。
- 在深度 d 处恰有
![img]() 个结点。
个结点。 - 根的度数为 k,它大于任何其他节点的度数;如果根的子女从左到右的编号设为 k-1, k-2, …, 0,子女 i 是子树 Bi 的根。
上图 (b) 表示二项树 B0 至 B4 中各节点的深度。图 (c) 以另外一种方式来看二项树 Bk。
在一棵包含 n 个节点的二项树中,任意节点的最大度数为 lgn。
二项堆
二项堆 H 由一组满足下面的二项堆性质的二项树组成。
- H 中的每个二项树遵循最小堆的性质:节点的关键字大于等于其父节点的关键字。
- 对于任意非负整数 k,在 H 中至多有一棵二项树的根具有度数 k。
第一个性质告诉我们,在一棵最小堆有序的二项树中,其根包含了树中最小的关键字。
第二个性质告诉我们,在包含 n 个节点的二项堆H中,包含至多 floor(lgn)+1 棵二项树。
![img]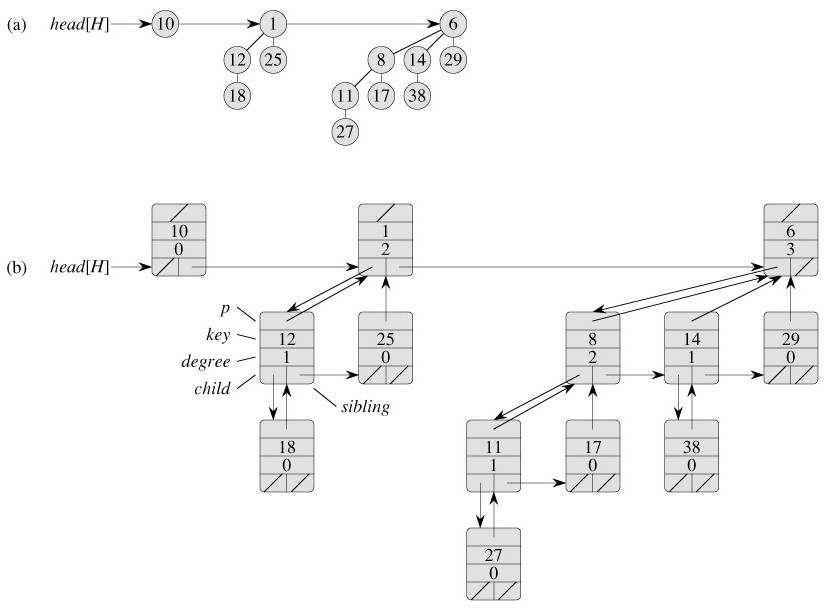
比如上图中一个包含 13 个节点的二项堆 H。13的二进制表示为(1101),故 H 包含了最小堆有序二项树B3,B2 和 B0, 他们分别有 8,4 和 1 个节点,即共有 13 个节点。
五个基本操作[2]
-
创建空堆
-
取最小值:由于二项树满足最小堆性质,所以遍历根表即可。
-
合并两个二项堆
step1:按照二项树的度递增的顺序合并两个根表。
step2:根表调整,以满足度的唯一性。用三个辅助指针(per、p、after)将度重复的树合并。
由于step1合并后的根表中,度相同的树最多有两颗,所以会出现以下几种情况:
case1:三个指针所指二项树根都存在,且度不同 => 指针后滑,进入case3或结束。
case2:per为空,p.degree = after.degree,且after.sibling存在 =>指针后滑,进入case4。
case3:case1或case2不成立,若pre为空,则一定有p.degree = after.degree => 根据degree
合并p和after所指二项树,after后滑,进入case2 或 case1
case4:三个指针所指二项树根都存在,且度相同 =>根据degree合并p和after所指二项树,after
后滑,进入case3。![二项堆插入]()
-
插入结点x
将x放入一个空堆H2中,将H和H2合并。
时间复杂度为O(lgn) -
抽取最小值结点
step1:遍历根表查最小值结点z。
step2:在根表中删除结点z,并把z的孩子"逆放"到一个空堆H2中。所谓逆放,即使H2满足二项堆根
表中树根的度递增的顺序。
step3:将H和H2合并。
时间复杂度O(lgn)
两个扩展操作
- 减值(减少结点z的key)
z减值后自底向上迭代比较,直到孩子结点的值大于父结点。类似冒泡。
时间复杂度;O(lgn) - 删除结点z
step1:对z进行减值操作,将z的值减为最小值。
step2:对z所在二项树的树根执行抽取操作。
时间复杂度:O(lgn)
二叉堆、二项堆、斐波那契堆(简称Fib堆)的比较:
相同:
- 都是可归并堆(Mergeable Heap);
- 它们都支持5个基本操作(创建、插入、查找最小值、抽取最小值、合并堆)和2个扩展操作
(结点减值、结点删除)。
不同:
- 二叉堆是一种结点有序的完全二叉树,可采用数组结构存储,通过数组下标索引结点,分最大
堆和最小堆。 二项堆和Fib堆都是最小堆。 - 二项堆由二项树组成,结构比二叉堆复杂,但其堆合并操作的时间复杂度较好。当堆合并操作
较多时,可使用二项堆。反之,使用二叉堆即可。
斜堆(Skew Heap)[3]
斜堆(Skew heap)也叫自适应堆(self-adjusting heap),它是左倾堆的一个变种。斜堆的节点没有"零距离"这个属性,Skew Heaps是对Leftist Heaps的改进。
左偏树的性质:
-
本节点的键值key小于其左右子节点键值key(与二叉堆相同);
-
本节点的左子节点的距离大于等于本节点的右子节点(这意味着每个节点中除了要存储键值外, 还需要一个额外的dist存储距离);
-
节点的距离是其右子节点的距离+1(这意味着, 一个节点的dist是从它出发到达最近终端节点的距离);
斜堆的性质:
-
本节点的键值key小于其左右子节点键值key;
-
斜堆节点不存储距离dist值, 取而代之的是在每次合并操作时都做swap处理(节省了存储空间);
左偏树(堆)merge的具体实现:
采用递归实现;
- 每层递归中, 当roota->val > rootb->val时, 交换roota和rootb;
- 向下递归;
- 如左子节点距离小于右子节点距离, 交换左右子节点;
- 更新本节点距离值;
- 返回本节点指针;
斜堆merge函数具体实现:
递归实现(也有非递归算法);
- 每层递归中, 当roota->val > rootb->val时, 交换roota和rootb;
- 向下递归;
- 交换左右子节点;
- 返回本节点指针;
非递归实现(更繁琐,并且需要外部排序):
- 把所有节点的右子树分离出来。
- 把分离出来的子树按根节点元素升序(广义上的升序)排列。
- 从后向前,把倒数第二个树左右子树交换,把最后一个树作为倒数第二个树的左子树。
(可以用栈实现,如果降序排列的话就可以用堆实现)
│ h1_heap.py 堆
│ h2_min_heap.py 最小堆
│ h3_max_heap.py 最大堆
│ h4_binomial_heap.py 二叉堆
│ h5_skew_heap.py 斜堆
│ __init__.py
│ 堆Heap.md 学习笔记


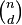 个结点。
个结点。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号