P2871 [USACO07DEC] Charm Bracelet S

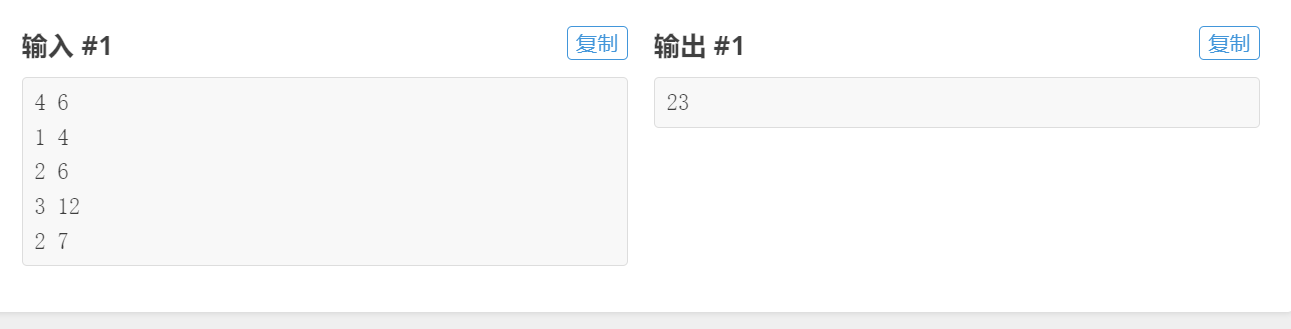
所以这是一个01背包的裸题，每个物品选与不选

dp[i][j] 在前面i个物品选择，在不超过j的前提先所能选到的最大价值

公式就出来了 dp[i][j] = max(dp[i-1][j],dp[i-1][j-t[i]]+w[i])

这是01背包的递推公式

注意的是，该公式还可以优化，因为第i个是从第i-1个递推过来的，并且只与第i-1个有关，所以可以用滚动数组，消去一维

动态规划表达式变为dp[i] 容量为i的情况下所能拿到的最大价值

dp[i] = max(dp[i],dp[i-t[i]]+w[i])

#include<bits/stdc++.h>
using namespace std;
const int N=5000;
int t[N],w[N];
int dp[N<<2];
int main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>t[i]>>w[i];
	}
	for(int i=1;i<=n;i++){
	   for(int j=m;j>=t[i];j--){
	   	  dp[j]=max(dp[j],dp[j-t[i]]+w[i]);
	   }
	}
	cout<<dp[m];
	return 0;
}