算法时间复杂度分析

1.算法复杂度的几种情况：

• 算法完成工作最少需要多少基本操作，即最优时间复杂度
• 算法完成工作最多需要多少基本操作，即最坏时间复杂度
• 算法完成工作平均需要多少基本操作，即平均时间复杂度

由于最优时间复杂度和平均时间复杂度都无法涵盖所有情况下算法的完成执行的可能，故在实际运用中，更关注最坏时间复杂度。

2.算法时间复杂度的几条基本计算规则

• 基本操作，即只有常数项，认为其时间复杂度为O(1)
• 顺序结构，时间复杂度按加法进行计算
• 循环结构，时间复杂度按乘法进行计算
• 分支结构，时间复杂度取最大值
• 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
• 在没有特殊说明时，算法的时间复杂度都是指最坏时间复杂度

3.常见时间复杂度

• 执行次数	阶	非正式术语
  10	O(1)	常数阶
  2n+1	O(n)	线性阶
  n2+n+1	O(n2)	平方阶
  10+log2n	O(logn)	对数阶
  n+nlog2n+10	O(nlogn)	线性对数阶
  n3+n2+n+1	O(n3)	立方阶
  2n	O(2n)	指数阶

  注意，经常将log₂n（以2为底的对数）简写成logn

 4.常见时间复杂度之间的关系

• 

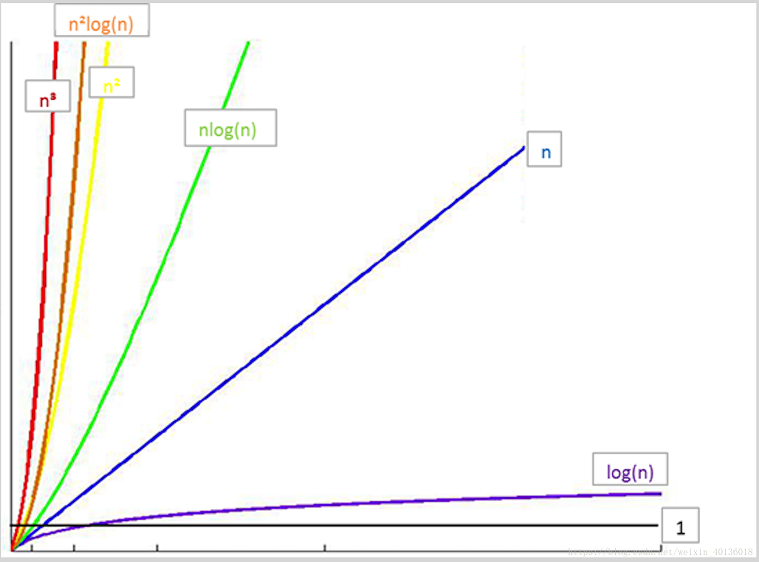
  所消耗的时间从小到大
  O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)