rrt Rapidly-exploring Random Tree using rtree
RRT is a random search algorithm, used to find a path from the start point to the target.
it can be describe like:(pseudo code)
while the termination didn't meet: new_node, nearest_node = get_new_and_nearest() if check(new_node, nearest_node): connect_to_nearest(new_node, nearest_node)
and here is a example code, where we can see how it built the tree clearly. Github link click here. This example code usde rtree -- a kind of data structure to store and search obestacles and the rrt which already built.
def rrt_search(self): """ Create and return a Rapidly-exploring Random Tree, keeps expanding until can connect to goal https://en.wikipedia.org/wiki/Rapidly-exploring_random_tree :return: list representation of path, dict representing edges of tree in form E[child] = parent """ self.add_vertex(0, self.x_init) self.add_edge(0, self.x_init, None) while True: for q in self.Q: # iterate over different edge lengths until solution found or time out for i in range(q[1]): # iterate over number of edges of given length to add x_new, x_nearest = self.new_and_near(0, q) if x_new is None: continue # connect shortest valid edge self.connect_to_point(0, x_nearest, x_new) solution = self.check_solution() if solution[0]: return solution[1]
this function describe a general procedure of the rrt algorithm, the key points are find a new node outside of the tree, if it could be connected to the rtree, the find a nearest node in the tree, then, connected this two nodes.
def new_and_near(self, tree, q): """ Return a new steered vertex and the vertex in tree that is nearest :param tree: int, tree being searched :param q: length of edge when steering :return: vertex, new steered vertex, vertex, nearest vertex in tree to new vertex """ x_rand = self.X.sample_free() x_nearest = self.get_nearest(tree, x_rand) x_new = self.bound_point(steer(x_nearest, x_rand, q[0])) # check if new point is in X_free and not already in V if not self.trees[0].V.count(x_new) == 0 or not self.X.obstacle_free(x_new): return None, None self.samples_taken += 1 return x_new, x_nearest
def nearby(self, tree, x, n): """ Return nearby vertices :param tree: int, tree being searched :param x: tuple, vertex around which searching :param n: int, max number of neighbors to return :return: list of nearby vertices """ return self.trees[tree].V.nearest(x, num_results=n, objects="raw") def get_nearest(self, tree, x): """ Return vertex nearest to x :param tree: int, tree being searched :param x: tuple, vertex around which searching :return: tuple, nearest vertex to x """ return next(self.nearby(tree, x, 1))
here, environment model denoted as X, and the vertex collection of the rtree denoted as V, these two variables both used rtree as data structure.
R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons.
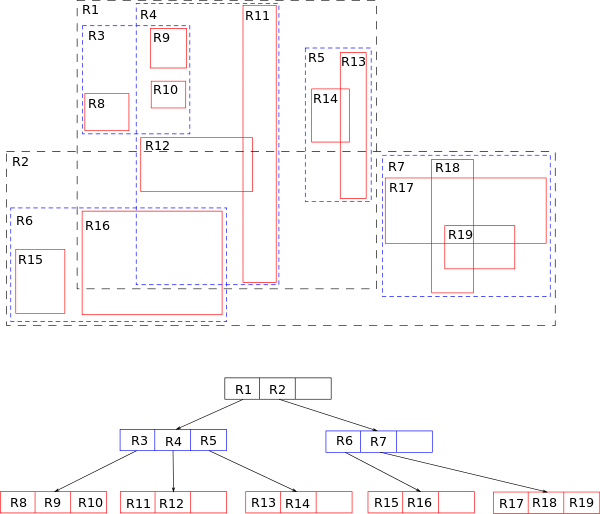
just like B-tree, R-tree is a balanced tree either.
rtree.index.nearest()
Returns the k-nearest objects to the given coordinates in increasing distance order.
This is currently not implemented for the TPR-Tree.
after we got the new_node and nearest node, we will check it first, if the new_node already in the tree.V? if the connection will confilct with the obsetacles in the environment status X?
if the condition is meet, the connection the two nodes and add the new_node in the vertex set tree.V
continue this loop until the target is found, then we tracebake from the target to the start-point through child node to the parent node.
def check_solution(self): # probabilistically check if solution found if self.prc and random.random() < self.prc: print("Checking if can connect to goal at", str(self.samples_taken), "samples") path = self.get_path() if path is not None: return True, path # check if can connect to goal after generating max_samples if self.samples_taken >= self.max_samples: return True, self.get_path() return False, None
def get_path(self): """ Return path through tree from start to goal :return: path if possible, None otherwise """ if self.can_connect_to_goal(0): print("Can connect to goal") self.connect_to_goal(0) return self.reconstruct_path(0, self.x_init, self.x_goal) print("Could not connect to goal") return None
def reconstruct_path(self, tree, x_init, x_goal): """ Reconstruct path from start to goal :param tree: int, tree in which to find path :param x_init: tuple, starting vertex :param x_goal: tuple, ending vertex :return: sequence of vertices from start to goal """ path = [x_goal] current = x_goal if x_init == x_goal: return path while not self.trees[tree].E[current] == x_init: path.append(self.trees[tree].E[current]) current = self.trees[tree].E[current] path.append(x_init) path.reverse() return path
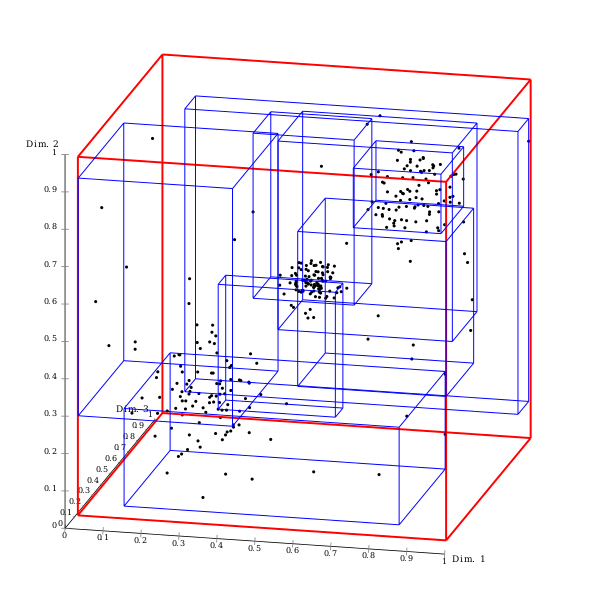
finally, let's think why should we use rtree? cause if we use rtree as datastructure, once we write the logical procedure of rrt, the code could be generalized to multi dimensions.

