DS博客作业05--树
1.本周学习总结
1.思维导图
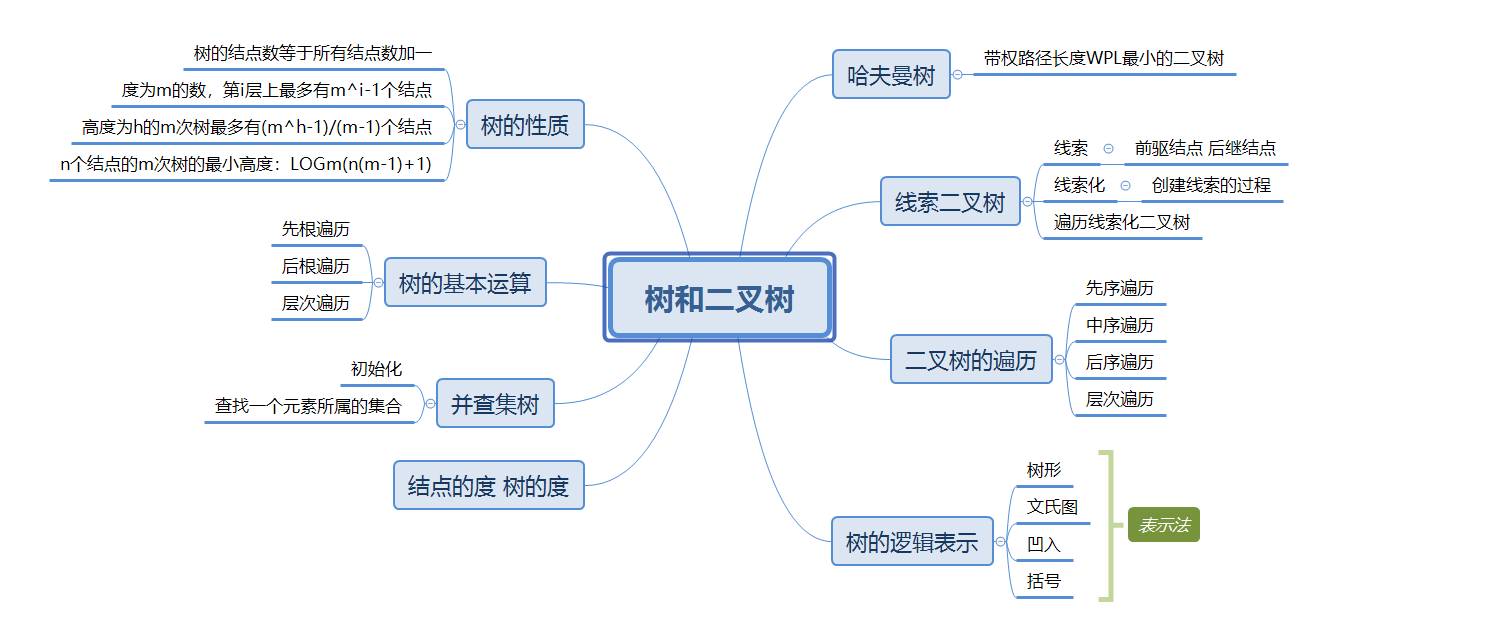
2.谈谈你对树结构的认识及学习体会
本章是对于二叉树的学习，刚开始预习的时候看到了遍历二叉树，理解很简单，但是将理解的内容运用到代码里还是有点难度的。在不断的百度和查书的过程中循序渐进。树在代码的长度上确实不长，但是它的运用不是很好理解，基本都是递归，想要过树这一关，一定要熟练掌握递归的运用。
2.PTA实验作业
2.1.题目1：题目名称:7-1 还原二叉树
2.1.1设计思路（伪代码）
定义两个数组a,b存放先序和中序的序列
int N;
cin >> N;
cin >> a;
cin >> b;
length即为先序序列的长度
if (length == 0)
return NULL;
BT *T = new BT;
T->data = a[0];
int i = 0;
for i = 0 to i = length
{ 找到先序i的在中序的位置
if (b[i] == a[0]) break;
}
T->lchild = FindTree(a+1, b, i);
T->rchild = FindTree(a + i + 1, b + i + 1, length - i - 1);
递归法判断是否到树的底部
return T;
int a = 0, b = 0;
if bt == NULL
return 0;
else
{
a = GetHeight(bt->lchild);
b = GetHeight(bt->rchild);
return (a > b) ? (a + 1) : (b + 1);
计算并返回二叉树最高的高度
}
end if 最后输出高度
2.1.2代码截图
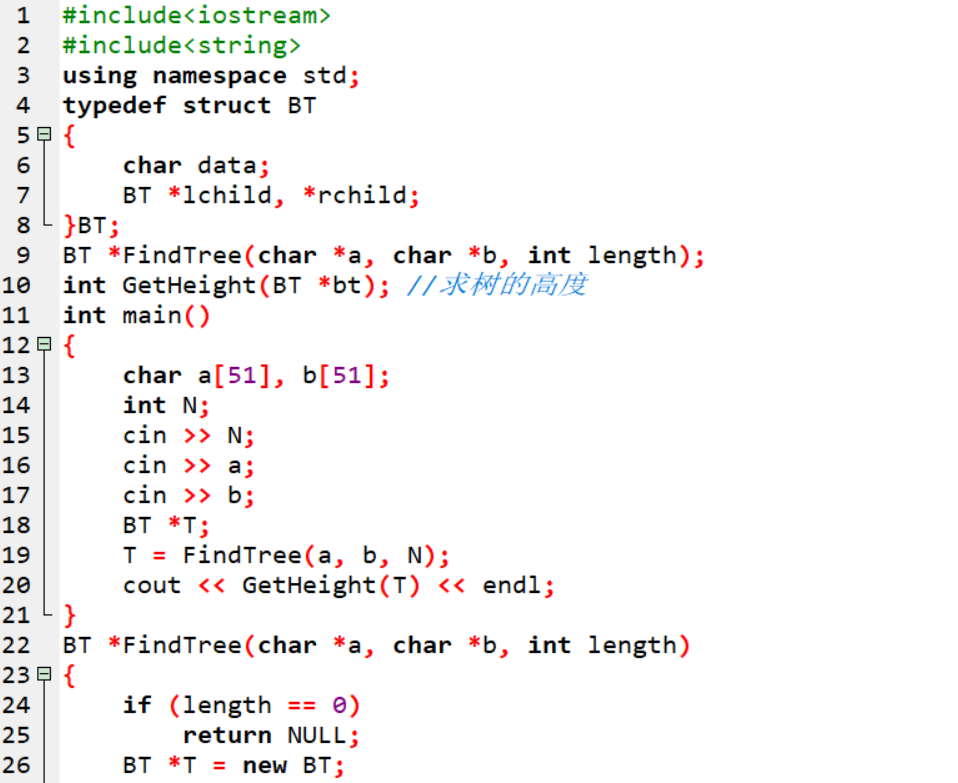
2.1.3本题PTA提交列表说明。
Q：建树后怎么求得最大高度？
A：使用递归不断判断是否到达底端。
2.2.题目2：7-4 jmu-ds-二叉树叶子结点带权路径长度和
2.2.1设计思路（伪代码）
首先定义结构体用于储存二叉树
length; 定义全局变量高度，求带权长度和时使用
BinTree CreateBTree(string str, int i, int h);
定义 find(BinTree T); 建树
定义函数 wpl(BinTree T); 求和、
BinTree CreateBTree(string str, int i, int h)
{
if i < 0 且 i >= length do
返回 NULL;
end if
if str[i] == '#'
返回 NULL;
end if
定义结构体变量 t，并赋予空间;
用来储存二叉树
返回 t;
}
void find(BinTree T)
{
if (T == NULL) return;
if (T->data != '#') cout << T->data;
find(T->left);
find(T->right);
}
int wpl(BinTree T)
{
if T == NULL
返回 0;
end if
if T->left == NULL 且 T->right == NULL
返回 ((T->data - '0')*T->high);
end if
返回 (wpl(T->left) + wpl(T->right));
}
2.2.2代码截图
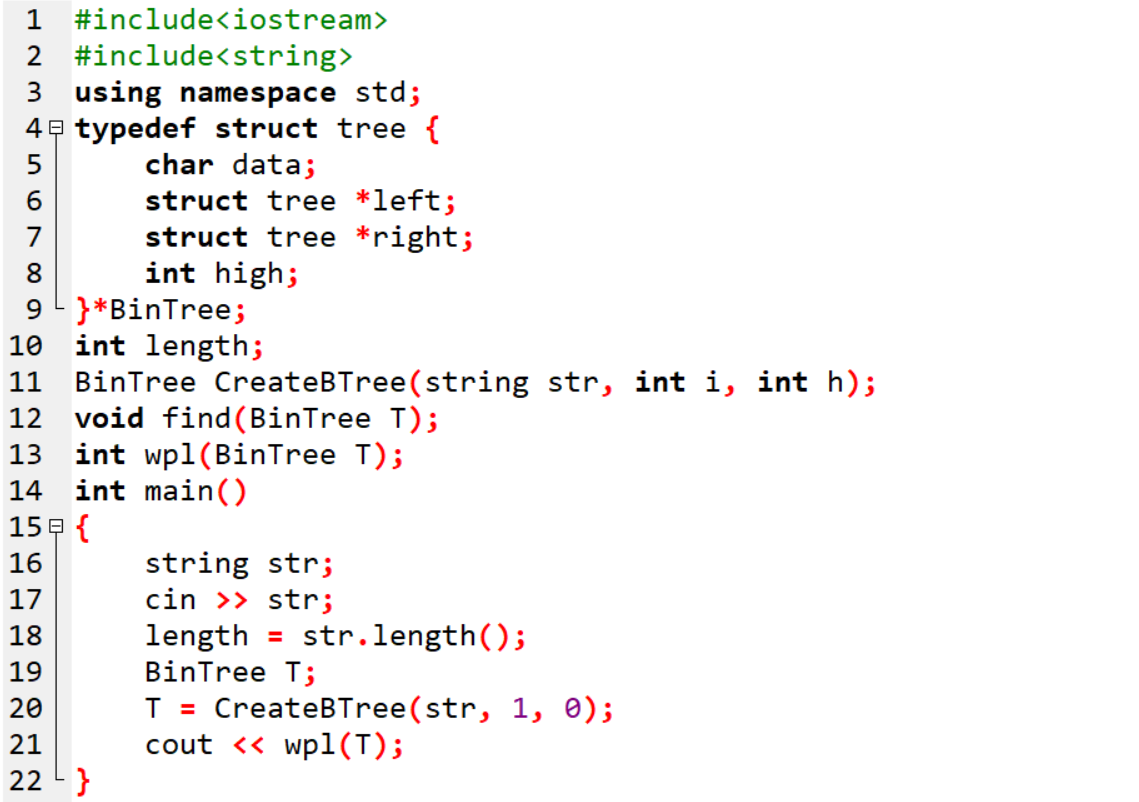
2.2.3本题PTA提交列表说明。
刚开始在树的建立上出现了错误，递归的时候错了！后来改了。递归还真的不简单，要不断地去看什么时候返回，返回的什么值。
2.3.题目3：题目名称：7-6 修理牧场
2.3.1设计思路（伪代码）
用 C++优先队列 来排列输入的一串数字
priority_queue<int, vector<int>, greater<int>> q;
cin >> n; 输入n用来确定输入的个数
for i = 0 to i = n
输入每段木块的长度 并记录到q中
s 初始化用来计算最小金额
for i = 1 to i = n-1
每次出队两个元素并相加，再将相加后值入队
s加上两元素相加后的值
end for
输出最小金额s
2.3.2代码截图
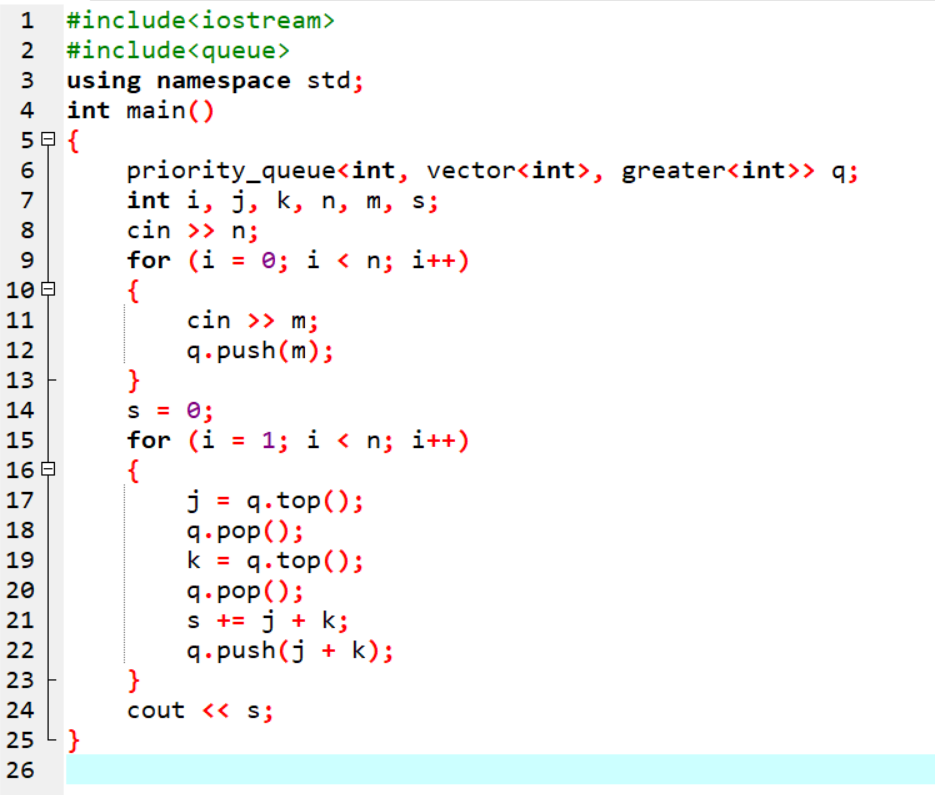
2.3.3本题PTA提交列表说明
Q：看到题目的时候就感觉是哈夫曼树，但找不到代码去搞定？
A：后来看同学的代码发现可以用队列来做
3.阅读代码
3.1 题目:平衡二叉树的判定
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
即二叉树任意一个节点其左子树深度与右子树深度相差不大于1：
递归方法求解（深度优先搜索）
3.2 解题思路
定义dfs函数用来找到高度，然后在用递归法判断左右子树的高度是否为相差不大于一，判断是否为平衡二叉树。
3.3 代码截图
3.4 学习体会
本题主要使用了递归算法配合二叉树的高度进行判断。
二叉树的遍历有多种，各有各的优点，而且还要懂得如何使用给出的遍历序列来得到二叉树也是很重要的。遍历之后就是要对遍历得到的数据进行处理，比如说高度计算、元素查找、哈夫曼树等等算法。
