贝叶斯分类器学习笔记

本文是结合周志华老师的《机器学习》和刘未鹏的《数学之美番外篇：平凡而又神奇的贝叶斯方法》http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/学习所得。如有不妥，敬请指正。

 

1. 参考资料

周志华老师的《机器学习》

数学之美番外篇：平凡而又神奇的贝叶斯方法，http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/

感谢二位提供的学习资料。

2. “逆向概率”问题

什么是“正向概率”，什么是“逆向概率”问题呢？

一所学校里面有 60% 的男生，40% 的女生。男生总是穿长裤，女生则一半穿长裤一半穿裙子。有了这些信息之后我们可以容易地计算“随机选取一个学生，他（她）穿长裤的概率和穿裙子的概率是多大”，这个就是前面说的“正向概率”的计算。然而，假设你走在校园中，迎面走来一个穿长裤的学生（很不幸的是你高度近似，你只看得见他（她）穿的是否长裤，而无法确定他（她）的性别），你能够推断出他（她）是女生的概率是多大吗？

 

计算正向概率：P(pants) = 60%*100% + 40%*50% = 80%，也就是这个人穿裤子的概率是80%。

计算逆向概率：P(girl | pants) = 穿长裤的女生/穿长裤的人 = P(girl, pants)/P(pants) = P(girl)*P(pants | girl) / P(pants) = 40% * 50% / 80% = 25%.

 

计算逆概率的两个公式就是贝叶斯公式：

1)  P(girl | pants) = P(girl, pants)/P(pants)

2)  P(girl | pants) = P(girl)*P(pants | girl) / P(pants)

 

3 . 贝叶斯公式的计算

在上面的例子中，pants其实就是类别c，取值是{长裤，裙子}。人是样本x，样本的特征是性别，只有这一维特征，取值是{男生，女生}。

进一步推广，如果我们的样本不是一维的，而是高维的，那怎么办？如果样本的特征不是离散而是连续的怎么办？

 

按照周志华老师的写法：

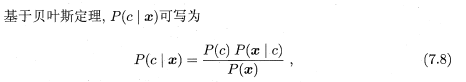
P(c|x)叫后验概率，也就是我们要计算的逆向概率，知道样本，计算这个样本属于某个类别的概率，概率最大的那个类别是最可能正确的类别。

P(c)是类“先验”概率。

P(x|c)是条件概率，也就是在类别c的条件下，出现样本x的可能性。如果是男生，穿裙子的概率是0，如果是女生，穿裙子的概率是50%。

 

P(c)表达了样本空间中各类样本所占的比例，根据大数定律，当训练集包含充足的独立同分布样本时，P(c)可通过各类样本出现的频率来估计，也就是个类别样本数/总样本数，就是每个类别的先验概率。以后不管计算哪个样本的后验概率，这个P(c)都用一样的值。

当然也有不同的情况，比如Latent Dirichlet Allocation(LDA)模型，就是假设每篇文档都有一个主题分布，但是具体到某一篇文档，这个分布是根据一个Dirichlet分布产生的。假设每篇文档都有3个主题，文档x1的主题分布是（1，0，0），文档x2的主题分布可以不同，比如是（0，1，0）.

 

对于类条件概率P(x|c)就不能用频率来估计概率了，因为数出来很有可能大部分都是0，特别是样本x是高维度的。

假设有d个属性，每个属性取值为{0，1}，那么x就有2的d次方种可能的取值方式。比如d=3，x的取值可以是：

（0，0，0）,（0，0，1）,（0，1，0）,（1，0，0）,（1，1，0）,（0，1，1）,（1，0，1）,（1，1，1）,一共8种取值方式。 

试想一下，对于文本向量，动不动就是几十万维度，这个组合多可怕。现在来了一篇新的文档x，这篇文档x的特征（词和词的顺序）极有可能在训练集中从来没有出现过，那频率就是0，这样所有的测试样本的条件概率几乎都等于0，这样的频率当然不能用来代替概率。

 

所以接下来就是来解决如何计算类条件概率，一种是极大似然估计方法，一种是朴素贝叶斯方法。

 

3.1极大似然估计方法

极大似然估计假设类条件概率符合某种分布，然后利用训练数据估计出分布的参数，供测试数据使用。

假设P(x|C)具有确定的形式并且被参数向量Θc唯一确定，则我们的任务就是利用训练集D估计参数Θc。

 

上面的两个公式中，均值向量的计算就是把所有属于类别c的训练的特征向量相加，处于c类样本总数，得到均值向量。对于方差也按照公式计算。

其实这里的思路是：

1）首先认为数据都是采样得到的，我们只能观测到一部分。是啊，我们的训练数据都是有限的，只能部分反应问题。

2）然后，还假设数据产生于某个分布，比如正态分布。这个假设有点勉强，为什么一定是某个分布产生的呢？万一真实问题很复杂，根本无法用一个分布描述呢？不过这样的假设还是可以接受。

3）要特别注意，分布选的好不好，能不能反映问题空间，将直接影响最终效果。比如我假设身高服从正态分布，然后利用训练数据估计出正态分布的两个参数，最后算出类条件概率，最后用类条件概率乘上类先验概率，就得到了后验概率，预测的效果也很好。但是如果身高不服从正态分布，出来的预测效果可能就很不好。

 

3.2 朴素贝叶斯方法

极大似然估计假设样本之间是独立的，也就是我的身高和你的身高完全没有关系，你的身高和第三个人的身高完全没有关系。

朴素贝叶斯方法更狠，假设属性之间相互独立。例如身高由{父母身高，吃的好坏，家庭收入}三个因素相关，这里只是示意，不一定就是这三个因素决定身高。“吃的好坏”和“家庭收入”很明显有较强的相关性，家庭收入高的，很有可能吃得也要好一点。但是朴素贝叶斯不管，认为这两个没有关系。就像上面举例说的文本中的词一样，明显词和词之间是有相关性的，但是朴素贝叶斯就是不考虑，认为属性之间相互独立。

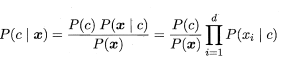
看到上面这个公式，一切都简单了，既然属性间相互独立，那么数据就没有那么稀疏了，我们就可以用频率代替类条件概率了。假设x是词汇向量，我们就可以一个词一个词的数，第一个词在每个类中出现的词数，初一这个词总共出现的词数，就等于P(xi | c). P(xi | c) = count(xi, c) / count(xi)。

 

最后计算一篇文档的后验概率就是将类条件概率相乘，再乘以类先验概率。当然对于每个类，P（x）都是一样的，因此不乘也罢，不影响最后比较大小。

虽然朴素贝叶斯的假设很不靠谱，但是在很多应用上效果还不错。关于这个问题还有理论解释，参见:http://www.cs.unb.ca/~hzhang/publications/FLAIRS04ZhangH.pdf. 

这个问题我没有深入研究，不过我认为这个还是要具体情况具体分析，也许在某些情况下朴素贝叶斯效果根本就不行。再说了，效果好与不好也不完全由分类器决定，特征也很重要。

 

不过遇到问题，朴素贝叶斯分类器绝对值得一试，知道这个结论就够了。

 

3.3. 半朴素贝叶斯分类器

为了对朴素贝叶斯的假设作改进，半朴素贝叶斯假设局部属性之间相互有关系，其他的属性之间相互独立。这就是语言模型嘛，这个词的类条件概率和前面的若干个词相关，但是并不是和其它所有的词都相关。

 

3.4. 贝叶斯网

这个又对半朴素贝叶斯分类器的假设进一步改进，属性之间的关联可以用一个网络结构来描述。比如文本里面，我可以让每个词x都与文章开头的几个词有关联，并不仅仅局限于只于x之前的几个词相关联。

这是西瓜书上的例子。

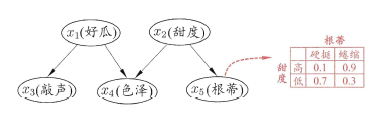
贝叶斯网可以将人的先验知识很自然的加入到模型中，这在实际应用时非常关键，我现在还没有用过，但是希望以后能够在这个方法上有所尝试。也许在社会网络关系的分析上，不一定要用pageRank，可以试试贝叶斯网。

 

最后周志华老师的书还谈了EM算法，以前学习LDA的时候看过，知道可以用Gibbs采样求解，比EM的效果好，速度快，所以就没有太关注。

 

整篇文章把极大似然估计，朴素贝叶斯，半朴素贝叶斯，贝叶斯网都当成是贝叶斯的求解，放到第三小节下面，不知道这样是否妥当。3.1-3.4都是为了能够算出类条件概率P（x | c），引入了一些假设使得模型可计算，这篇文章的脉络也是我现在对贝叶斯方法的一个整体认识，可能有点简单，希望以后能够更加深入。