0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结图内容
图
- 定义:图是顶点和边的集合,存储多个点之间的关系,简单来说就是多对多的关系。
- 分类:
- 有向图:点之间的边有方向。边用尖括号"<>"表示。(术语:“弧”,表示有方向的边)
- 无向图:点之间的边没有方向。边用圆括号"()"表示。
- 术语:
- 邻接点:不论是无向图还是有向图,边的两个顶点互为邻接点。
- 度:无向图中,某点所连接的边叫做这个点的度;有向图中,以某点为边的起点的边数叫做这个点的出度,以某点为边的终点的边数叫做这个点的入度,入度和出度的和是这个点的度。
- 度和边的关系:所有点的度之和/2=图的边数
- 完全图:每两个点之间都有边(无向图是一条边,有向图是两点之间互相指向对方的两条边)。设某图有n个顶点,若是完全无向图,它有n(n-1)/2条边;若是完全有向图,它有n(n-1)条边。
- 稠密图和稀疏图:稠密图就是接近于完全图的图;稀疏图就是边数远小于完全图边数的图。
- 路径:一个点到另一个点所经过的顶点序列。
- 路径长度:就是一条路径上所经过的边的数目。
- 简单路径:除起始点和结束点可以相同,整条路径经过的点都不能相同。
- 回路/环:就是起始点和结束点相同的路径。
- 权:如果图的边是有数值的,这个数值就叫权,而这种图叫做带权图,也可以称作网。
- 连通
- 无向图的连通,就是某两点之间有路径,就可以说它们之间是连通的。如果在某个图中,任意两点都连通,这个图就可以叫做连通图,如果不是,则叫做非连通图。连通分量是无向图中极大的连通子图,简单来说,就是把一个图,分块,每块的点都可以最大限度地构成连通图。
- 有向图中,如果任意两点都存在有向路径,则说明这个图是强连通图,如果不是,则这个图所有的强连通子图叫做它的强连通分量。找强连通分量,其实就是在找回路。
- 连通图,最多有n(n-1)/2条边,最少有n-1条边。
图存储结构
邻接矩阵
- 用二维数组来表示边。下标表示顶点,比如数组egde[i][j]表示的是i到j的边的情况,有边则数据不为0,无边则数据为0。注意,点到本身也是没有边的,即edge[i][i]=0.
- 定义:
#define MAXV 最大顶点个数
typedef struct {
int number;/*顶点编号*/
/*顶点其他信息*/
}VertexType;
typedef struct {
int edges[MAXV][MAXV];/*邻接矩阵*/
int n, e;/*顶点数、边数*/
VertexType vexs[MAXV];/*顶点信息*/
}MatGraph;
一般可简化成:
typedef struct
{ int edges[MAXV][MAXV]; /*邻接矩阵*/
int n,e; /*顶点数、弧数*/
} MGraph;
-
比如:
- 无向图:(有对称性)
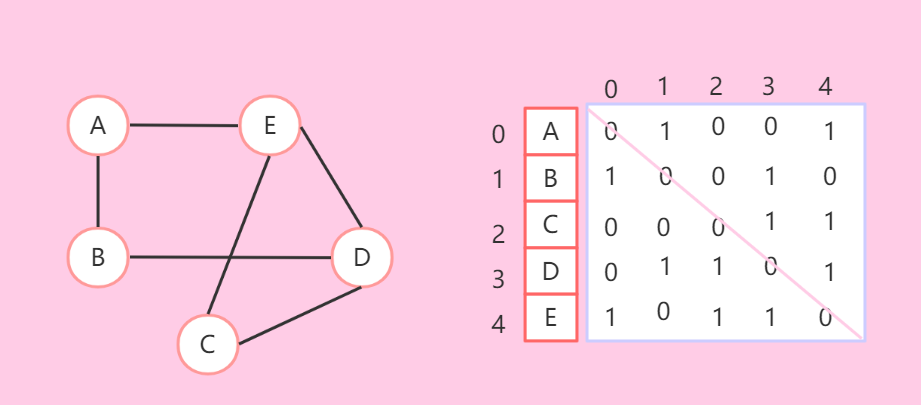
- 有向图:(不一定对称)
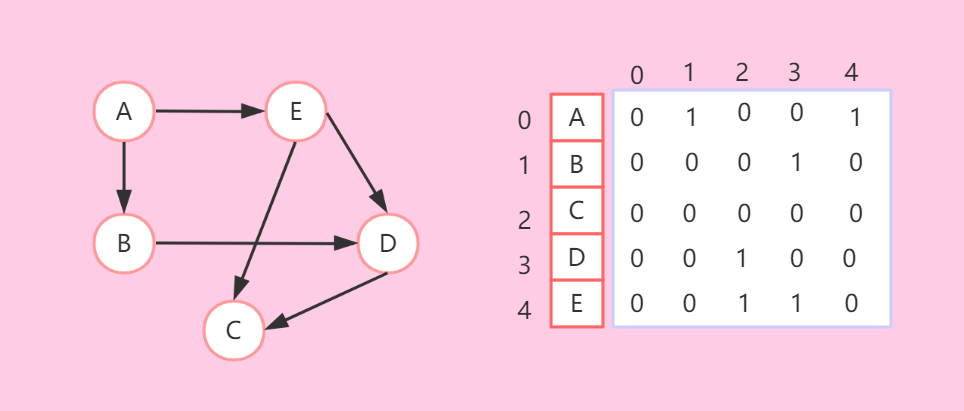
- 无向图:(有对称性)
-
特点:邻接矩阵是唯一的,它适用与稠密图的存储。空间复杂度为O(n²),其中n为顶点个数。
邻接表
- 结合数组和链表的方法来存储。每个顶点有一个单链表,连接这个顶点的所有邻接点,然后将这些顶点的单链表的头结点存到一个数组中。
- 定义:
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode* nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode* firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{
AdjList adjlist; //邻接表
int n, e; //图中顶点数n和边数e
} AdjGraph;
- 比如:
-
无向图:

-
有向图:
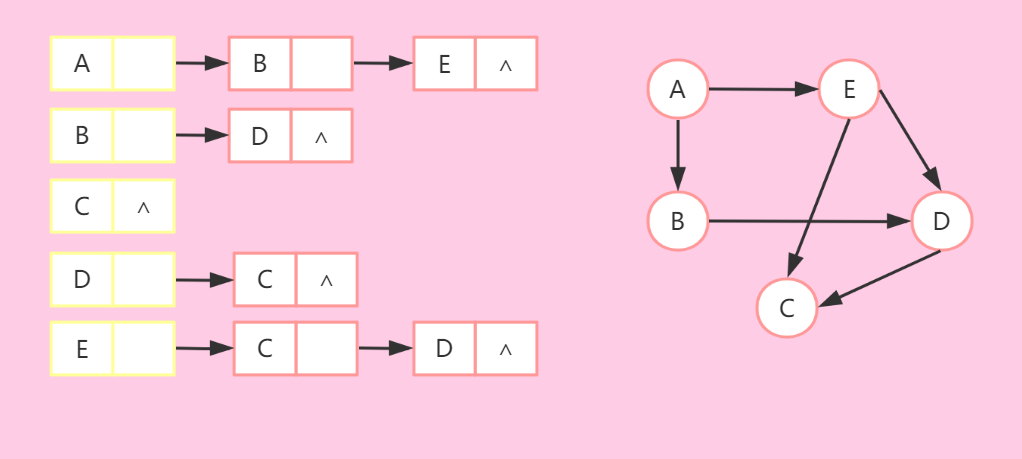
-
- 特点:邻接表不唯一,它比较适合稀疏图的存储,空间复杂度为O(n+e),其中n为顶点个数,e为边数。
图遍历及应用
DFS(深度优先遍历)
- 就是选定一个点,然后遍历它的一个邻接点,再继续遍历这个邻接点的邻接点,以此类推。在遍历的过程中,还需要保证每个点只遍历一次,直到所有点都遍历过为止。
- 比如:

- 具体代码的实现:

- 应用:
- 判断是否连通:进行一次深度遍历,同时记录路径visited[顶点],如果是连通图,它的深度遍历就可以经过图中所有的点,如果不是连通图,那么它就无法遍历所有的顶点,visited数组会存在数值为0的点。
- 具体代码:
bool check(AdjGraph* G)
{
int i;
bool flag = true;
for (i = 0; i < G->n; i++)/*初始化visited数组*/
{
visited[i] = 0;
}
DFS(G, 起始点);
for (i = 0; i < G->n; i++)
{
if (visited[i] == 0)/*出现为0的点说明不连通*/
{
flag = false;
break;
}
}
return flag;
}
- 找路径:从起始点开始遍历,到遇到终点的时候停止。方法:用一个数组来存路径,在原函数的基础上加上出口,即遇到终点时结束程序,输出存放路径的数组。代码实现如下:
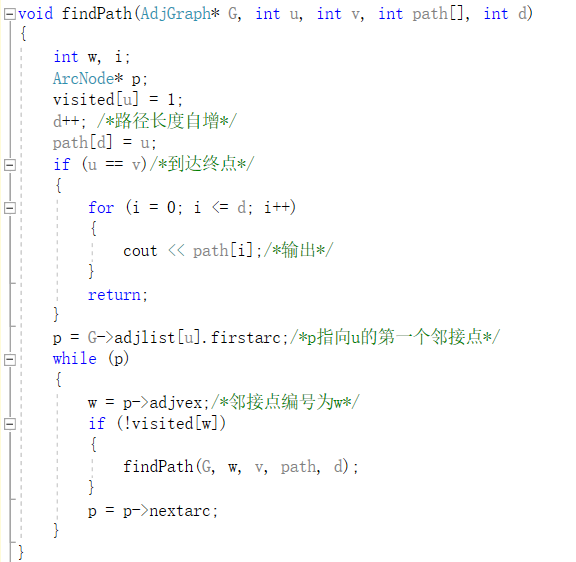
注:如果要找多条路径,则在函数末尾加上visted[u]=0.
BFS(广度优先遍历)
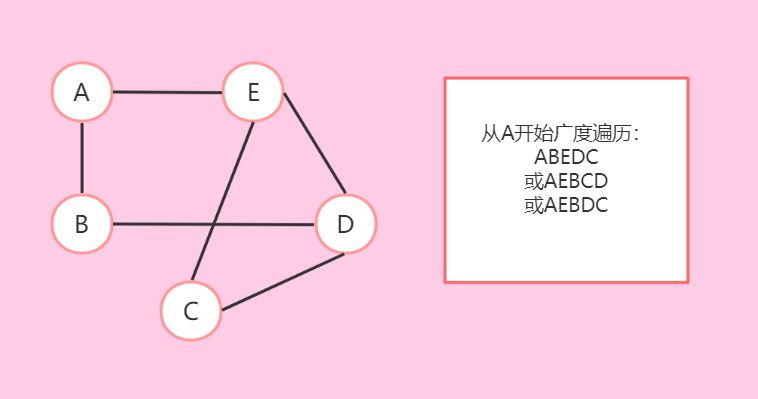
- 就是从某一点开始,访问它的所有邻接点,然后按它访问邻接点的顺序,接着访问它的邻接点的所有邻接点,每次遍历要考虑每个点只遍历一次。类似树结构的层次遍历。
- 比如:
- 具体的代码实现:

- 最短路径:(类似之前的树结构学的迷宫)
最小生成树相关算法及应用
- 生成树是图中的一个最小连通子图,它的边为n-1,且不为回路。
- 遍历产生的生成树:深度优先遍历得到的称为深度优先生成树,由广度优先遍历得到的生成树称作广度优先生成树。生成树不唯一(如下图所示)

- 权值之和最小的称为最小生成树。
普利姆算法(prim)
-
思路:
- 给定一个图,和一个起始点x。初始化U,使得U={x}。
- 在x到其他顶点的边里,选择最小的那条边,并得到x的邻接点y,将y放入U中。
- 判断y的加入是否产生了更短的路径,如果有更短的路径,修改候选边。
- 重复2、3两步直到所有的点都在U中为止。
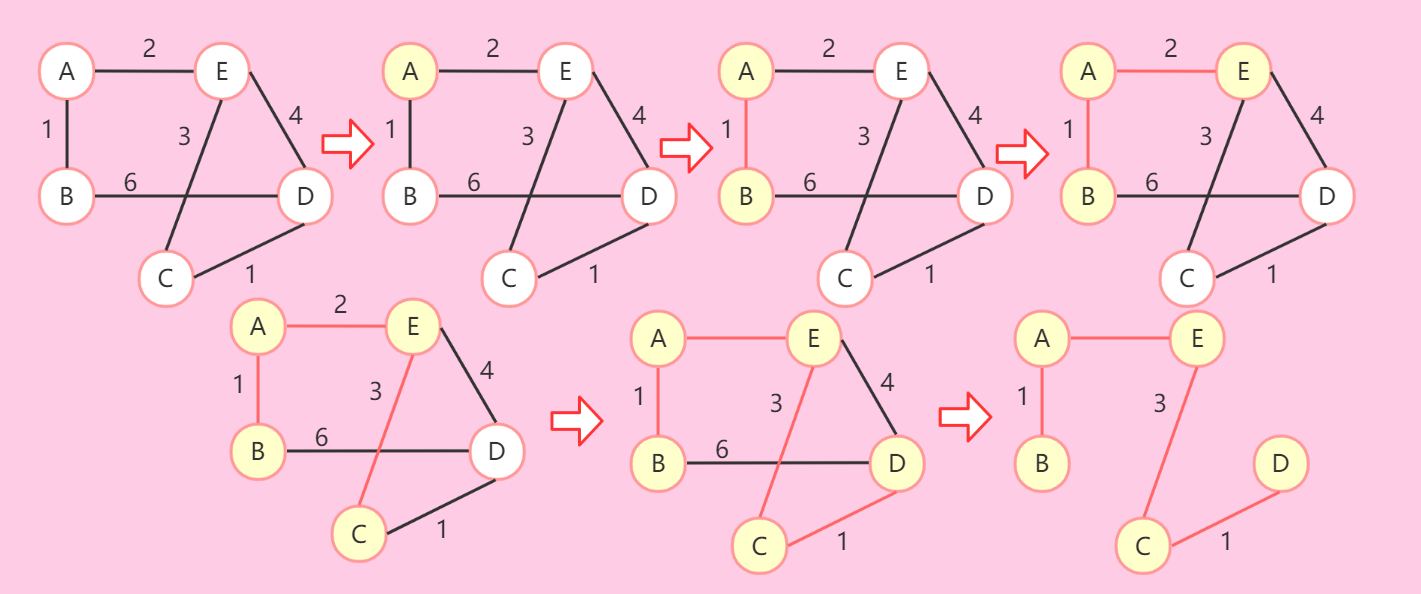
-
具体代码:

-
应用:pta 7-4 公路村村通
主要代码如下:

克鲁斯卡尔算法(Kruskal)
-
思路:
- 给定一个图,无需知晓起始点
- 在所有边里找最小边,并将其标记,如果这个边没有让这个图产生回路,则可以把它加入生成树。
- 重复第2步,直到生成树包含所有的点为止。
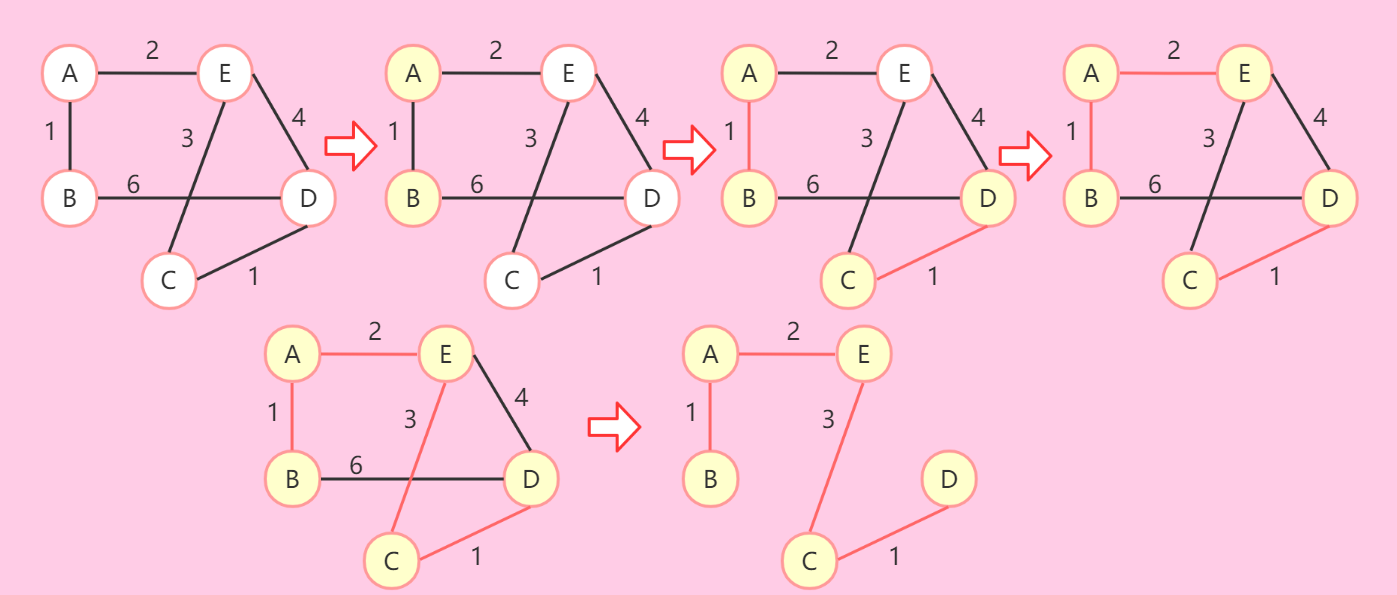
-
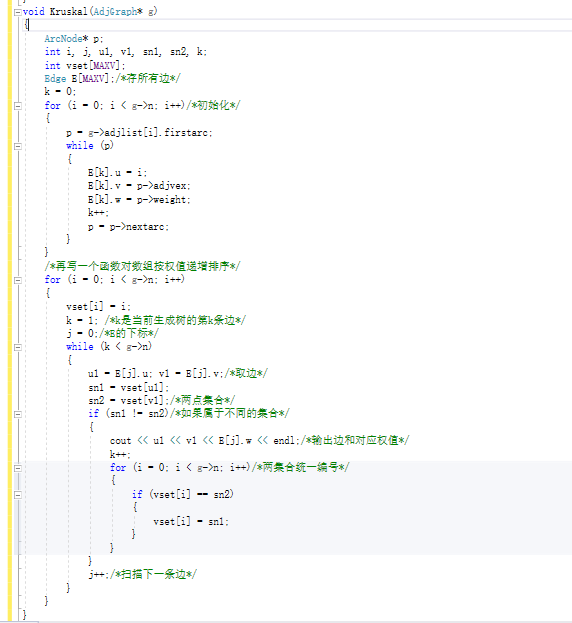
具体代码:
- 边的存储:
typedef struct
{
int u;/*边的起点*/
int v;/*边的终点*/
int w;/*边的权值*/
}Edge;
Edge E[MAXV];
最短路径
- 最短路径与最小生成树不同,它的路径上不一定有n个点。
Dijkstra算法(迪杰斯特拉)
-
思路:
- 确定起始点x,存入S中;
- 找x连着的边里最小的那条,得到邻接点y。
- 把邻接点加入S中,同时判断它的加入是否会出现更短的路径,如果有更短的路径,则修改路径。
- 重复2、3步直到S中包含所有顶点。
-
具体代码:
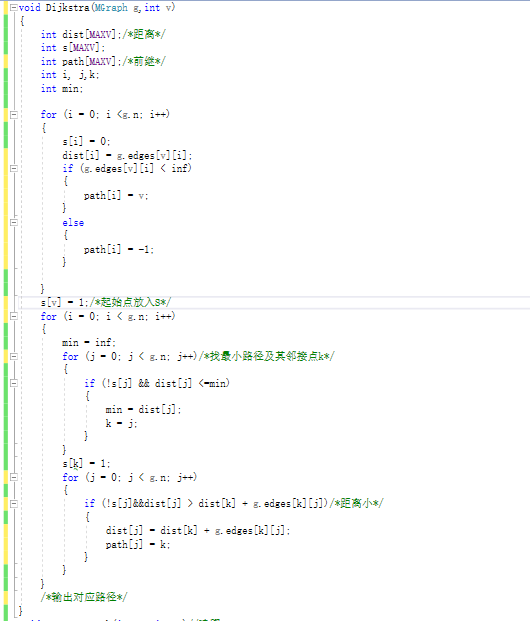
-
应用:pta 7-6 旅游规划
- 主要代码:

- 主要代码:
Floyd算法(弗洛伊德)
- 思路:(找任意两点的最小路径)
- 定义两个二维数组,A[i][j]表示顶点i到j的最短路径长度,path[i][j]表示对应路径的前继。
- 考虑顶点x,思路有点像Dijkstra,修改数组A和path,(与这个点相关的路径长度不变,比如下标中有x的)
- 重复考虑点直到所有点都遍历过。
- 最后,根据数组path从终点找前继,直到起点,对应点就是路径的逆序列。数组A[起点编号][终点编号]就是所求的路径长度。
- 时间复杂度:O(n³)
- 具体代码:

拓扑排序
- 拓扑排序,是在一个有向无环图中找拓扑序列,要保证每个点只出现一次,且如果有A到B的一条路径存在,A必须排在B前面。也就是被指向的必须排在后面。
- 思路:
- 在图中选取一个没有入度的点,输出它,然后删掉这给顶点以及它所有的有向边;
- 重复上述步骤,直到所有点都已经输出为止。

- 具体代码:
typedef struct/*头结点*/
{
int data;/*顶点编号*/
int count;/*顶点的入度*/
ArcNode* firstarc;/*指第一条边*/
}VNode;

- 注:如果要判断图是否有回路,可以在每次输出点的时候计数,如果最后输出点的个数与图中点的个数不同,则存在回路。原理是:拓扑排序输出的点的入度需要为0,如果存在回路,那么回路中的点的入度永远不可能为0,也就无法输出。
关键路径
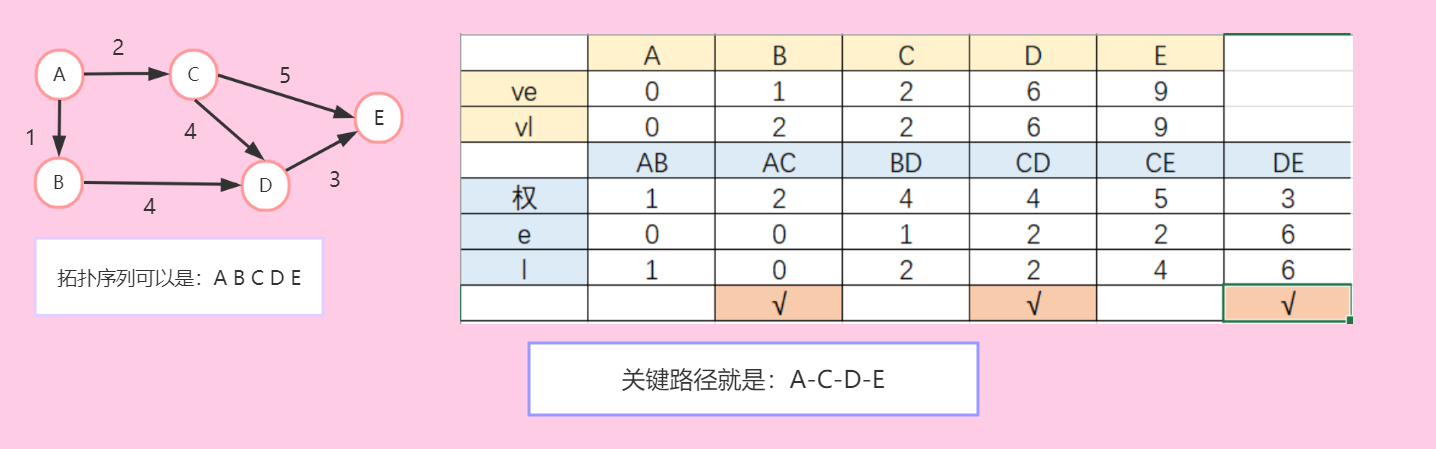
- 关键路径是指有向图中从源点到汇点的最长路径。其中,关键路径中的边叫做关键活动。
- 步骤:
- 对图进行拓扑排序。
- 在拓扑排序得到的序列的基础上,计算出边的最早开始时间和最晚开始时间,分别得到ve和vl数组。ve是当前点到起始点的最长路径,vl有点像是找当前点到终点的最长路径,然后用ve[终点]-最长路径;
- 计算所有边的e和l,其中,对边
,e=ve[i],l=vl[l]-边的权值 - 如果e=l,那么它就是关键活动,而所有的关键活动相连,就是它的关键路径。
1.2.谈谈你对图的认识及学习体会。
- 学习了图结构,我认为它的应用其实还是比较贴近生活的。我们平常的课程表需要的排课、用到的导航,都与它有关。主要是要理解那些算法的方法,我虽然感觉我有点理解了,但是在具体提到它们的时候,可能还是有一点混乱,容易忘记那个算法具体是怎么做的,就只记得大致的思路。图结构的话,如果结合图来看,对算法的思路会更加明确。有时候看不懂算法的思路,可以去参考下网络上其他人的博客,他们有画各种不同的图和对应步骤的变化图,能够帮助我们理解算法的核心思想,我个人觉得还是很有用的。在预习的时候,在自己看的不是很明白的时候,就可以参考其他人的博客,帮助理解,如果在老师上课前就弄明白了算法的大致思路,上课的时候效率也比较高。如果单看代码,可能就没有那么直观明了。多看几个例子,我们理解的才能比较清楚。在写了一些代码后,我觉着需要注意的一点是,要看清题目对顶点的编号,注意它是从0开始编号还是从1开始编号,然后根据具体的要求建图(决定要不要用到0这个下标),再根据创建的图来写那些操作代码。还有就是,在写代码的时候,有些功能的实现需要用到辅助数组,而如果这个数组的大小过大,(它是在函数中的局部变量)就会导致堆溢出,程序就会报错,无法运行,而解决的办法是,把它直接定义成全局变量。
2.阅读代码(0--5分)
2.1 题目及解题代码
-
题目

-
代码


2.1.1 该题的设计思路
- 分析:题目给了一个有向带权的图,需要解决两个问题:一是从给定的起始点到所有其他的点之间是否存在路径;二是需要求其他点到起始点的最短路径,并从这些最短路径中找到最大值。
- 思路:用到的是求最短路径的Dijkstra算法
- 从给定点k开始,选择与它最近的邻接点;
- 判断这个邻接点的加入是否使得更短路径出现,如果存在更短的路径,则更新路径信息。
- 重复上述过程,直到所有的点都遍历过为止。
- 判断点k到其他点是否都有路径,如果不是输出-1,如果是,取这些最短路径的最大值。
-时间复杂度:O(n²)空间复杂度:O(n²)
2.1.2 该题的伪代码
定义数组distance存放各点到起始点的最短路径长度,visited数组用来标记遍历过的点。
读取time数组构建图的邻接矩阵
for循环初始化distance
for 1 to n
for 1 to n+1
找到未遍历过的且距离起始点最近的邻接点minIndex;
end for
for 1 to n+1
判断与minIndex相连的边是否会使得各点到起始点的路径更短,如果是,更新distance数组
end for
end for
for循环遍历数组distance
if存在某个数据为-1,即某点与起始点之间无路径
输出-1
end if
else
取distance的最大值
end else
end for
2.1.3 运行结果

2.1.4分析该题目解题优势及难点。
- 优势:我们学过求最短路径的方法。
- 难点:主要是对算法的熟悉和应用,之前求最短路径的时候,基本不存在没有路径的问题,但其实解决有没有路径的问题,就隐藏在算法中,对distance数组的处理,就包括了无路径的问题。
2.2 题目及解题代码
-
题目

-
代码
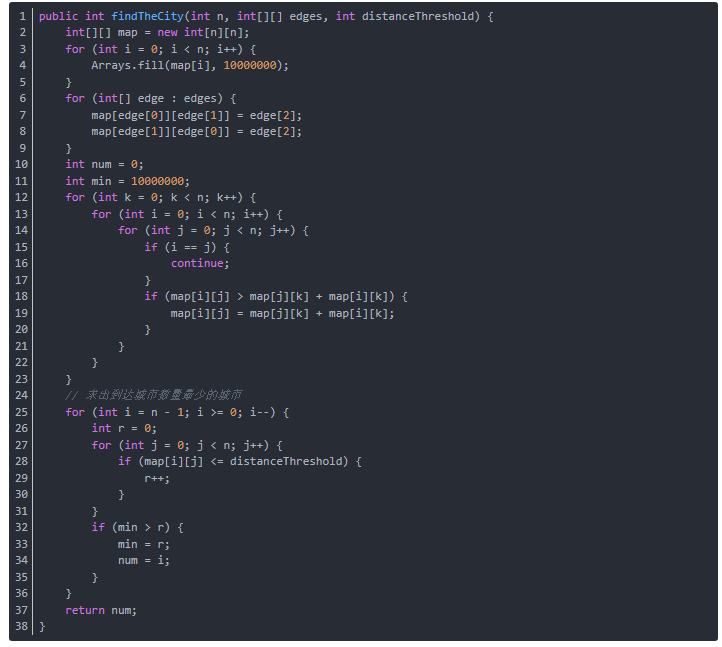
2.2.1 该题的设计思路
- 思路:
- 先用Floyd算法求出点与点之间的最短路径
- 根据所求的最短路径,计算在允许的最大范围内每个点能够去到的城市的个数
- 取城市个数最小的点(如果个数相同则取编号较大的那个点)
- 时间复杂度:O(n³)空间复杂度:O(n²)
2.2.2 该题的伪代码
定义二维数组map存点与点之间的最短路径长度
for循环初始化map数组
for 0 to n(k)
for 0 to n(i)
for 0 to n(j)
if i=j即不存在边
continue;
end if
else
判断k点的存在是否会有更短的路径出现(map[i][j] > map[j][k] + map[i][k]),如果存在,则修改map值
end else
end for
end for
end for
for n-1 to 0
for 0 to n
求在允许范围内的路径长度能到达的城市数量r
end for
比较min和r取最小值min并记录城市编号num
end for
return num;
2.2.3 运行结果

2.2.4分析该题目解题优势及难点。
- 优势:我们学过最短路径的算法,而且这道题题目就很明确表示出,我们需要求最短路径。
- 难点:选择什么方法来求最短路径,比如我们选的是Floyd算法,它的三层循环具体怎么操作。在规定长度内怎么算所能到达城市的数量。
2.3 题目及解题代码
-
题目:
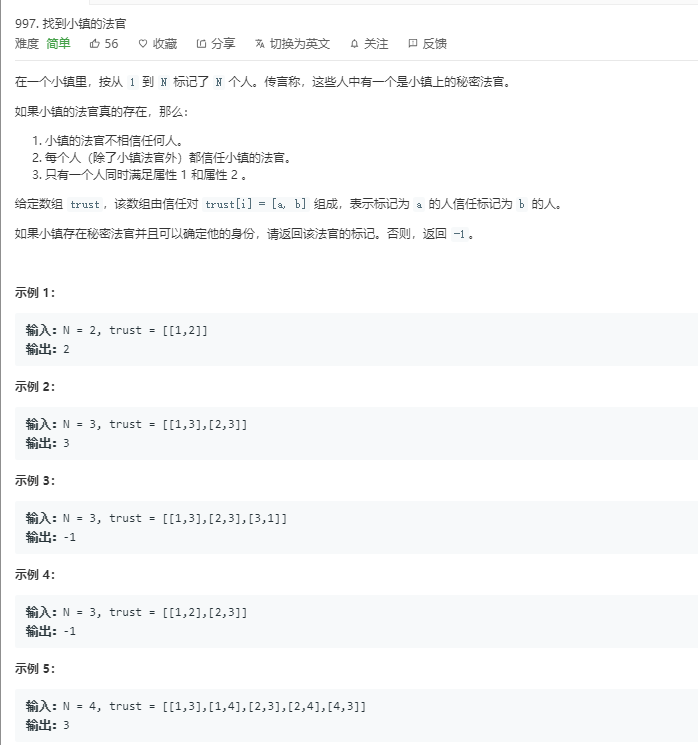
-
代码:


2.3.1 该题的设计思路
-
思路:题目中,法官是被其他人信任但不信任任何一个人的存在,在图中,就是出度为0入度为n-1的点。所以在邻接矩阵中,它所在的行对应的数据都为0(信任的人为0个),它所在的列,对应数据则都不是0.
-
时间复杂度:O(n²) 空间复杂度:O(n²)
2.3.2 该题的伪代码
for循环读取trust数组赋值给邻接矩阵对应的位置
for循环改邻接矩阵中自己对自己的信任为1
for 1 to n(j)
for 1 to n(i)
如果这一列中数都为1则是法官,否则break
end for
if 这一列满足是法官的条件即i>n
for 1 to n(k)
如果这一行数都为0且本身为1则是法官,否则break
end for
if 在行上也满足条件即k>n
保存这个点的编号为index
end if
end if
end for
return index
2.3.3 运行结果
2.3.4分析该题目解题优势及难点。
- 优势:这题如果用图来做,就是在考它的入度和出度的问题。还算是比较简单的。
- 难点:如何判断一个人是法官是本题的重点,把法官问题转换为入度出度问题,这个思路上的转变很关键。如果没想到这一层,就会有点难做。




