Tuning xgboost in R:Part 1

第一次调整Boosting算法的参数可能是一个非常艰难的任务。
有很多参数可供选择，调整不同的参数会有不同的结果产生。
最好的调参可能是取决于数据。
每当我得到一个新的数据集，我都会学到一些新的东西。
对分类和回归树（CART）有很好的理解有助于我们理解boosting

我最喜欢的Boosting包是xgboost，它将在下面的所有示例中使用。
在讨论数据之前，我们先谈谈一些我认为最重要的参数。
这些参数大多用于控制模型适合数据的程度。
我们希望能够捕捉数据的结构，但仅限于真实的结构。
换句话说，我们不希望模型适合噪音（过拟合）

 

eta: 学习（或收缩）参数。
它控制Boosting中将使用来自新树的多少信息。
该参数必须大于0并且被限制为1.
如果它接近零，我们将仅使用来自每个新树的一小部分信息。
如果我们将eta设置为1，我们将使用新树中的所有信息。
eta的大值导致更快的收敛和更多的过度拟合问题。
小数值可能需要许多树来聚合。colsample_bylevel:就像随机森林一样，

有时候只需要看一些变量就可以增长树中的每个新节点。
如果我们查看所有变量，算法需要更少的树来收敛。
但例如，查看2/3的变量可能会导致模型更具鲁棒性以适应过度拟合。
有一个类似的参数叫做colsample_bytree，它重新采样每个新树中的变量，
而不是每个新节点。

max_depth : 控制树木的最大深度。 更深的树有更多的终端节点并且适合更多的数据。 如果我们深入发展，融合也需要更少的树木。 但是，如果树要深一些，我们将使用来自第一棵树的大量信息，算法的最终树对丢失函数的重要性将会降低。 Boosting从使用许多树木的信息中受益。 因此，巨大的树木是不可取的。 较小的树木也会增长得更快，并且因为Boosting在伪剩余中生长新的树木，我们不需要为单个树木进行任何惊人的调整。

 

sub_sample : 这个参数决定我们是估计一个Boosting还是一个随机Boosting。 如果我们使用1，我们会获得常规的Boosting。 0和1之间的值是随机的情况。 随机Boosting只使用一小部分数据来增长每棵树。 例如，如果我们使用0.5，每棵树将采样50％的数据增长。 随机增强是非常有用的，如果我们有异常值，因为它限制了它们对最终模型的影响，因为它们被放在几个子样本上。 而且，对于较小的实例，可能会有显着的改进,但它们更易于过度拟合。

 

gamma:控制在树中增长新节点所需的损失函数的最小减少量。 此参数对损失函数的规模很敏感，它将与响应变量的规模相关联。 使用不同于0的gamma的主要结果是停止生成无用的树的算法，这些树几乎不会减少样本内误差，并且可能导致过度拟合。 这个参数以后再说。

 

min_child_weigth :控制终端节点中观察值（实例）的最小数量。 此参数的最小值为1，这使得树只有一个观测值的终端节点。 如果我们使用更大的值，我们将限制可能的完美拟合。 这个参数也将留给第二部分。

 

example:

 

数据服从一下等式：

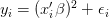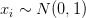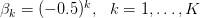   这里： ，。变量数量K将被设置为10，实例数量将被设置为1000。

 

实验将更改每个Boosting参数，使所有其他参数保持不变以尝试隔离其效果。 标准模型将具有以下参数：

eta:0.1

colsample_bylevel:2/3

sub_sample:0.5

我会将这些参数中的每一个更改为代码中的值。 我们将分析测试样本中的收敛性和均方根误差（RMSE）。 下面的代码将准备一切运行模型。

library(xgboost)
library(ggplot2)
library(reshape2)
library(Ecdat)
 
set.seed(1)
N = 1000
k = 10
x = matrix(rnorm(N*k),N,k)
b = (-1)^(1:k)
yaux=(x%*%b)^2
e = rnorm(N)
y=yaux+e
 
# = select train and test indexes = #
train=sample(1:N,800)
test=setdiff(1:N,train)
 
# = parameters = #
# = eta candidates = #
eta=c(0.05,0.1,0.2,0.5,1)
# = colsample_bylevel candidates = #
cs=c(1/3,2/3,1)
# = max_depth candidates = #
md=c(2,4,6,10)
# = sub_sample candidates = #
ss=c(0.25,0.5,0.75,1)
 
# = standard model is the second value  of each vector above = #
standard=c(2,2,3,2)
 
# = train and test data = #
xtrain = x[train,]
ytrain = y[train]
xtest = x[test,]
ytest = y[test]

　　

eta:我们将开始分析eta参数。 下面的代码估计每个候选eta的Boosting模型。 首先我们得到了收敛图，这表明eta的更大值收敛得更快。 然而，图下方的列车RMSE表明，更快的收敛并不能转化为良好的样本外表现。 较小的eta值如0.05和0.1是产生较小误差的值。 我的观点是，在这种情况下，0.1给我们一个良好的样本外性能和可接受的收敛速度。 请注意，eta = 0.5和1的结果与其他结果相比非常糟糕。

set.seed(1)
conv_eta = matrix(NA,500,length(eta))
pred_eta = matrix(NA,length(test), length(eta))
colnames(conv_eta) = colnames(pred_eta) = eta
for(i in 1:length(eta)){
  params=list(eta = eta[i], colsample_bylevel=cs[standard[2]],
              subsample = ss[standard[4]], max_depth = md[standard[3]],
              min_child_weigth = 1)
  xgb=xgboost(xtrain, label = ytrain, nrounds = 500, params = params)
  conv_eta[,i] = xgb$evaluation_log$train_rmse
  pred_eta[,i] = predict(xgb, xtest)
}

　　

conv_eta = data.frame(iter=1:500, conv_eta)
conv_eta = melt(conv_eta, id.vars = "iter")
ggplot(data = conv_eta) + geom_line(aes(x = iter, y = value, color = variable))

　　

(RMSE_eta = sqrt(colMeans((ytest-pred_eta)^2)))

##      0.05       0.1       0.2       0.5         1
##  9.964462 10.052367 10.223738 13.691344 20.929690

　　

colsample_bylevel:下一个参数控制每个新节点中测试的变量（特征）的比例。 回想一下，如果我们使用1，所有变量都经过测试。 小于1的值只测试相应的变量部分。 收敛性表明该模型对colsample_bylevel不太敏感。 具有较小值的曲线略高于具有较大值的曲线。 最准确的模型似乎是每棵树中使用25％样本的模型。 这个结果可能会随着不同类型的数据而改变。 例如，我们生成的数据使用相同的分布来创建所有响应变量，并且测试向变量赋予相似的权重，这使得采样不那么重要。

set.seed(1)
conv_cs = matrix(NA,500,length(cs))
pred_cs = matrix(NA,length(test), length(cs))
colnames(conv_cs) = colnames(pred_cs) = cs
for(i in 1:length(cs)){
  params = list(eta = eta[standard[1]], colsample_bylevel = cs[i],
              subsample = ss[standard[4]], max_depth = md[standard[3]],
              min_child_weigth = 1)
  xgb=xgboost(xtrain, label = ytrain,nrounds = 500, params = params)
  conv_cs[,i] = xgb$evaluation_log$train_rmse
  pred_cs[,i] = predict(xgb, xtest)
}

　　

conv_cs = data.frame(iter=1:500, conv_cs)
conv_cs = melt(conv_cs, id.vars = "iter")
ggplot(data = conv_cs) + geom_line(aes(x = iter, y = value, color = variable))

　　

 

 

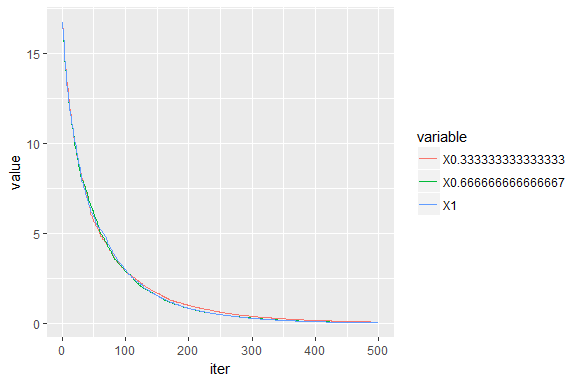
(RMSE_cs = sqrt(colMeans((ytest-pred_cs)^2)))

## 0.333333333333333 0.666666666666667                 1
##          10.29836          10.05237          10.20938

　　

max_depth:第三个参数是每棵树中允许的最大深度。 当然，如果我们种植更大的树木，模型会更快地收敛（见下图）。 但是，最好的示例外性能是max_depth = 4。 请记住，更大的树木更可能导致过度贴合。 根据我的经验，不需要使用大于4到6的值，但可能有例外。

set.seed(1)
conv_md=matrix(NA,500,length(md))
pred_md=matrix(NA,length(test),length(md))
colnames(conv_md)=colnames(pred_md)=md
for(i in 1:length(md)){
  params=list(eta=eta[standard[1]],colsample_bylevel=cs[standard[2]],
              subsample=ss[standard[4]],max_depth=md[i],
              min_child_weigth=1)
  xgb=xgboost(xtrain, label = ytrain,nrounds = 500,params=params)
  conv_md[,i] = xgb$evaluation_log$train_rmse
  pred_md[,i] = predict(xgb, xtest)
}

　　

conv_md=data.frame(iter=1:500,conv_md)
conv_md=melt(conv_md,id.vars = "iter")
ggplot(data=conv_md)+geom_line(aes(x=iter,y=value,color=variable))

　　

　　

(RMSE_md=sqrt(colMeans((ytest-pred_md)^2)))

##         2         4         6        10
## 12.502733  9.374257 10.134965 10.100691

　　

 sub_sample:下一个参数决定我们是否估计Boosting或Stochastic Boosting。 较小的值会导致样本中的误差更大，但它可能会产生更强大的样本外估计。 但是，如前所述，对于具有许多特征的样本，与观察次数和数据非常嘈杂时相比，您将获得更大的改进。 这里不是这种情况。 尽管如此，与确定性案例相比有一些改进，我相信这主要是由响应变量中的异常值引起的（boxplot变量y可以看到）。

set.seed(1)
conv_ss=matrix(NA,500,length(ss))
pred_ss=matrix(NA,length(test),length(ss))
colnames(conv_ss)=colnames(pred_ss)=ss
for(i in 1:length(ss)){
  params=list(eta=eta[standard[1]],colsample_bylevel=cs[standard[2]],
              subsample=ss[i],max_depth=md[standard[3]],
              min_child_weigth=1)
  xgb=xgboost(xtrain, label = ytrain,nrounds = 500,params=params)
  conv_ss[,i] = xgb$evaluation_log$train_rmse
  pred_ss[,i] = predict(xgb, xtest)
}

　　

conv_ss=data.frame(iter=1:500,conv_ss)
conv_ss=melt(conv_ss,id.vars = "iter")
ggplot(data=conv_ss)+geom_line(aes(x=iter,y=value,color=variable))

　　

 

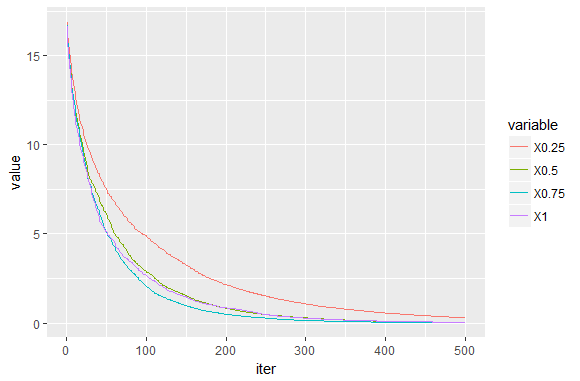
(RMSE_ss=sqrt(colMeans((ytest-pred_ss)^2)))

##      0.25       0.5      0.75         1
##  9.731273 10.052367 11.119535 11.233855

　　

这里的主要结论是，调整Boosting模型没有独特的规则。 最好的方法是测试几种配置。

请继续关注，如果你喜欢这篇文章，我们会尽快讨论Boosting。