查找

查找

查找：根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素或记录

查找表是由同一类型的数据元素构成的集合，集合中的数据元素是一种松散的关系


  • 静态查找表：仅作查询操作
  • 动态查找表：作插入和删除操作

关键字：

  • 主关键字：可唯一表示一个记录
  • 次关键字：可以识别若干记录

查找算法的评级指标：关键字的平均比较次数，也称平均查找长度ASL=期望


线性表的查找

顺序查找（线性查找）

  • 顺序表或线性表表示的静态查找表
  • 表内元素之间无序

typedef struct {
    int key;
}KeyType;

typedef struct {
    KeyType *R;         //表基质
    int length;         //表长
}SSTable;

int Search_Seq(SSTable ST,KeyType key){
    for (int i = ST.length; i >=1 ; i--) {
        if(ST.R[i].key==key.key) return i;
    }
    return 0;
}

每循环一次都要进行两次比较

改进：在0号位置加入要查找的key（监视哨），可以免去判断是否越界

当ST.length较大时，此改进进行一次查找的平均时间几乎减少一半

typedef struct {
    int key;
}KeyType;

typedef struct {
    KeyType *R;         //表基质
    int length;         //表长
}SSTable;

int Search_Seq(SSTable ST,int key){
    int i;
    ST.R[0].key=key;
    for (i = ST.length; ST.R[i].key!=key ; i--);
    return i;
}

比较次数与key位置有关：

  • 查找第i个元素，需要比较n+1-i次
  • 查找失败需要比较n+1次

时间复杂度O(n) ASL=（n+1)/2（等概率查找）

空间复杂度O(1) ：一个哨兵的辅助空间


当查找概率不等时：按查找概率高低存储

  • 查找概率越高，比较次数越少
  • 查找概率越低，比较次数越多

当查找概率无法确定时：按查找概率动态调整记录顺序


  • 优：算法简单，逻辑次序无要求，不同存储结构均适用

  • 缺：ASL太长，时间效率太低

    ​

折半查找（二分或对分查找）

有序表表示静态查找表

每次将待查记录所在区间缩小一半

每次用待查找的值与中间值（mid=(low+high)/2）进行比较

  • 小于：往左继续（high移到mid-1处）
  • 大于：往右继续（low移到mid+1处）

找到：mid==key；结束：high<low

int Search_Bin(SSTable ST,int key){
    int low=1,mid;
    int high=ST.length;
    while (low<=high){
        mid=(low+high)/2;
        if(key==ST.R[mid].key) return mid;
        else if(key>ST.R[mid].key) low=mid+1;
        else if(key<ST.R[mid].key) high=mid-1;
    }
    return 0;
}

判定树：

成功： 比较次数=路径上的结点数=结点的层数<=树的深度（log2 n +1）

不成功：比较次数=路径内部结点数<=log2 n +1

ASL=log2（n+1) -1

时间复杂度O(lgn)


  • 优：效率比顺序查找高

  • 缺：只适用于有序表，且限于顺序存储结构 （对链式存储结构无效）

    ​

分块查找（索引查找）

将表分成几块，块间有序，块内可无序

时间效率位于折半查找与顺序查找之间


  • 优：插入、删除比较容易，无需进行大量移动
  • 缺：要增加一个索引表的存储空间，并对其排序

适用于：既要快速查找，又要动态变化


顺序查找 折半查找 分块查找
ASL 最大 最小 中间
表结构 有序表、无序表 有序表 分块有序
存储结构 顺序表、线性链表 顺序表 顺序表、线性链表

树表的查找

改用动态查找表——特殊的树

表结构在查找过程中动态生成

给定值key，若表中存在则返回；不存在则插入关键字等于key的记录


二叉排序树

  • 若左子树非空，左子树上所有结点值均小于根结点的值

  • 若右子树非空，右子树上所有结点值均大于等于根结点的值

  • 左右子树又是一颗二叉排序树

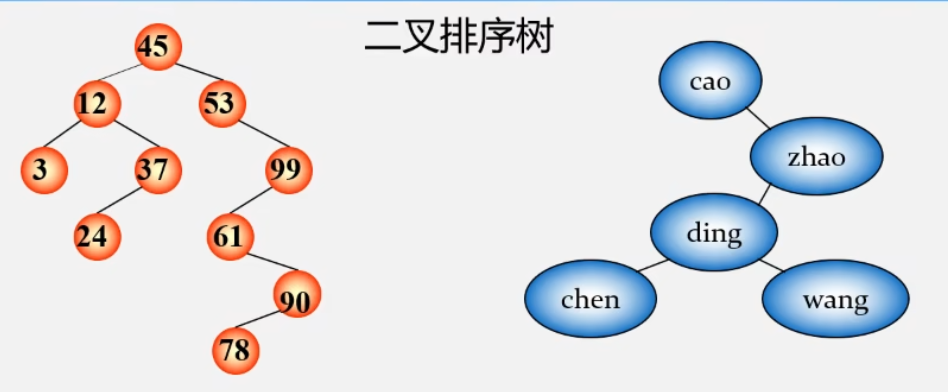
    image

中序遍历二叉排序树是一个按关键字排列递增有序的序列


查找步骤：

  • 查找的关键字等于根结点，成功
  • 查找的关键字等于根结点
    • 小于根结点，查其左子树
    • 大于根结点，查其右子树
  • 在左右子树上的操作类似
typedef struct {
    int key;
}KeyType;

typedef struct BSTnode{
    KeyType data;
    struct bSTnode *lchild,*rchild;
}BSTNode,*BSTree;

BSTree SearchBST(BSTree T,int key){
    if(!T||key==T->data.key) return T;
    else if(key<T->data.key) return SearchBST((BSTree) T->lchild, key);
    else if(key>T->data.key) return SearchBST((BSTree) T->rchild, key);
    return 0;
}

平均查找长度ASL与树的深度有关

  • 最好时：与折半查找的判定树相同，ASL=log2 (n+1) -1 ; 查找效率O(log2 n)
  • 最坏时：单支树形态，与顺序查找相同，ASL=(n+1)/2; 查找效率O(n)

二叉排序树的插入

步骤：

  1. 若二叉排序树为空，则插入结点作为根结点插入到空树中
  2. 否则，继续在其左、右子树上查找
    • 树中已有，不再插入
    • 树中没有，查找直至某个叶子结点的左子树或右子树为空为止，则插入结点应为该叶子结点的左孩子或右孩子

  • 一个无序序列可以通过二叉排序树变成一个有序序列，构造树的过程就是对无序序列进行排序的过程
  • 插入的均为叶子结点，无需移动其他结点
  • 关键字的输入顺序不同，建立的二叉排序树也不同

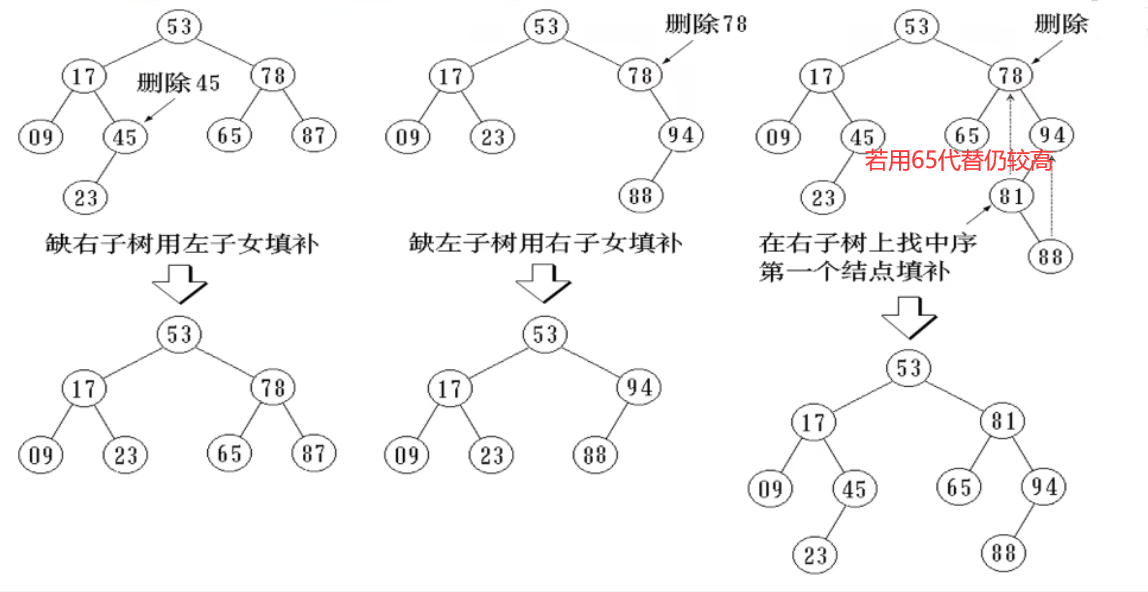
二叉排序树的删除： 高度不能增加

  • 删除叶子结点：直接删除（其双亲指针域值改为空）

  • 删除的结点只有左子树或右子树：用其左子树或右子树替换（其双亲结点的指针域指向删除结点的左子树或右子树）

  • 删除的结点既有左子树又有右子树：

    • 用左子树中最大结点代替，并删除左子树中最大结点
    • 用右子树中最小结点代替，并删除右子树中最小结点

  • image


平衡二叉树/AVL树

  • 是二叉排序树

  • 左子树与右子树的高度差的绝对值≤1

    平衡因子BF=左子树高度-右子树高度

  • 左子树和右子树也是平衡二叉排序树

对于一棵有n个结点的AVL树，其高度保持在O(log2 n)数量级，ASL也保持在O(log2 n)量级；查找性能最好的二叉排序树


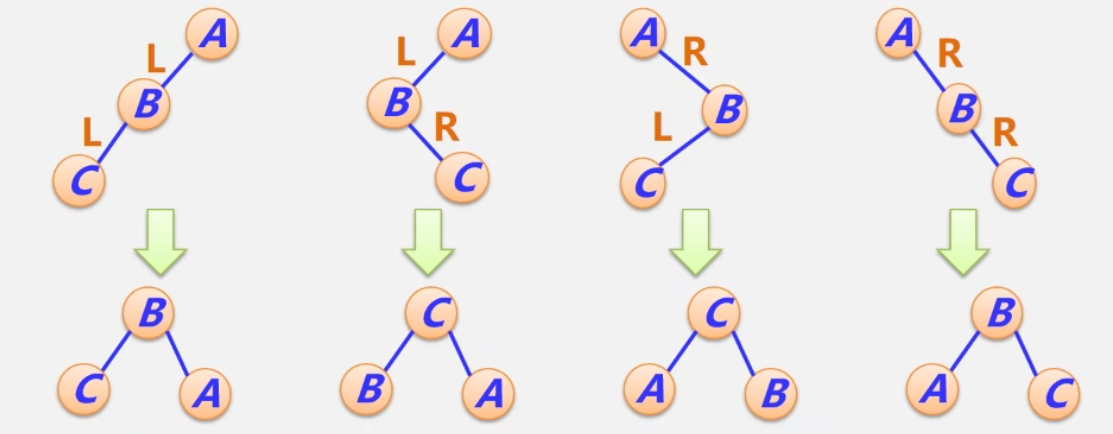
在平衡二叉排序树中插入新结点可能会导致失衡

当失衡结点不止一个时：找最小失衡子树的根结点

调整原则：降低高度；保持二叉排序树性质

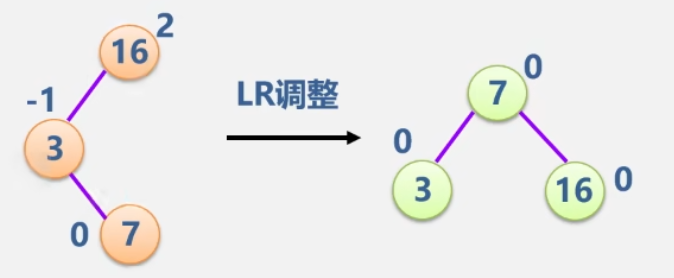
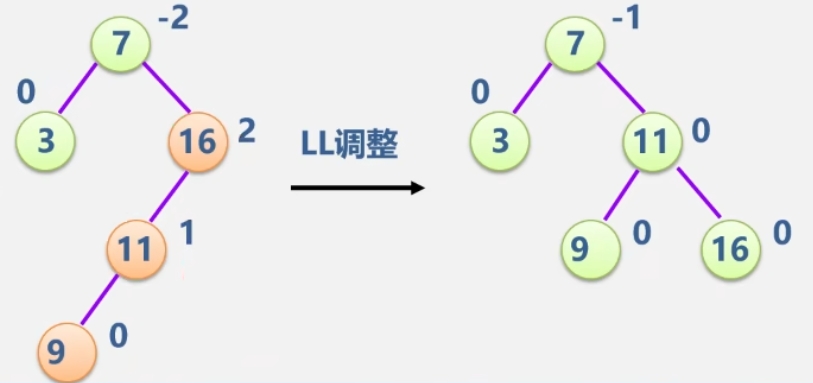
image

  • LL型

  • LR型

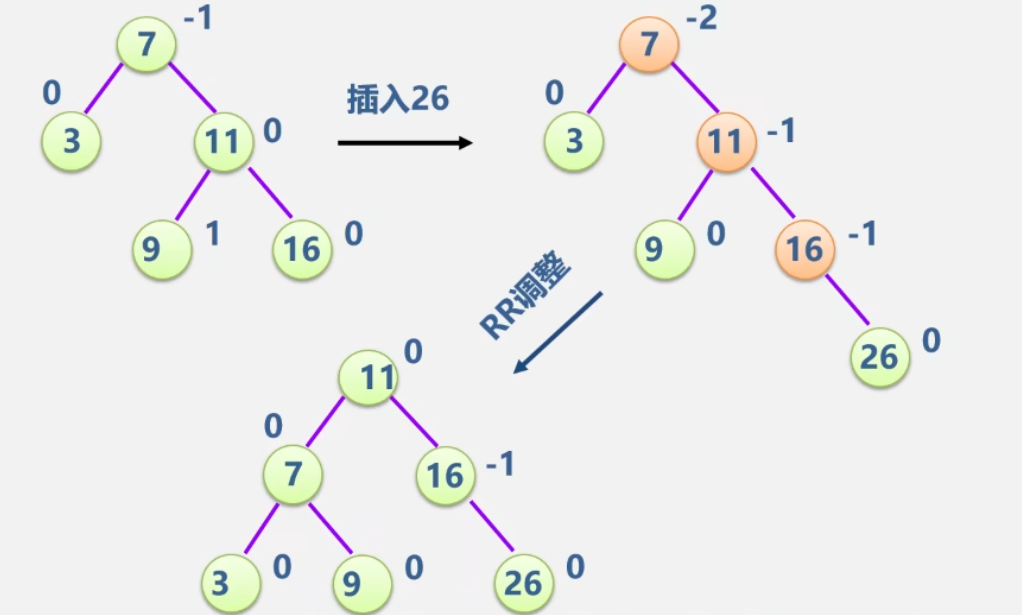
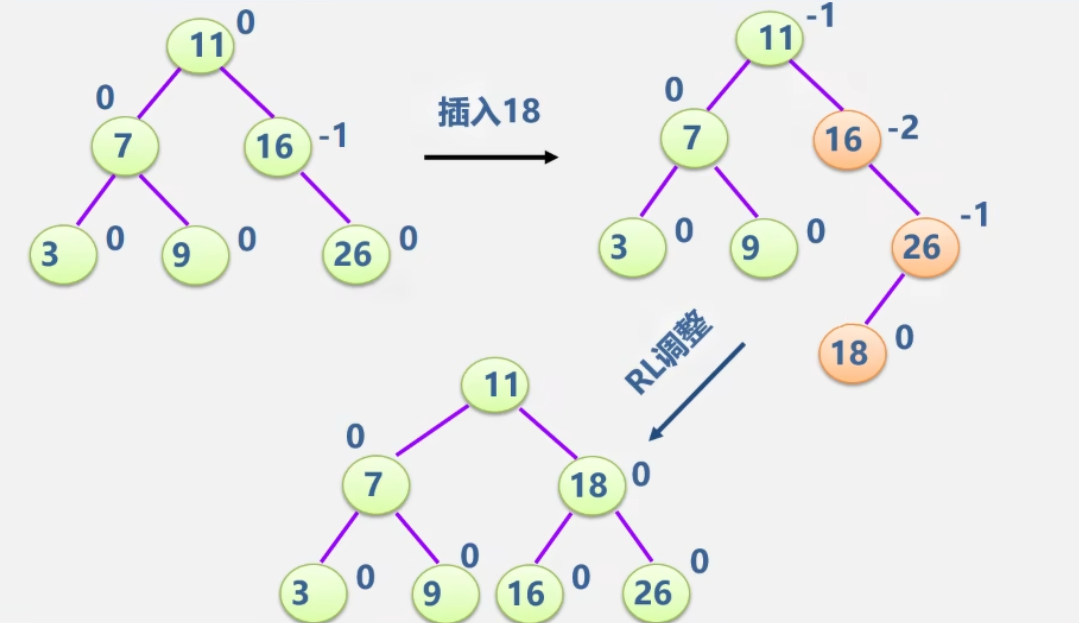
  • RL型

  • RR型
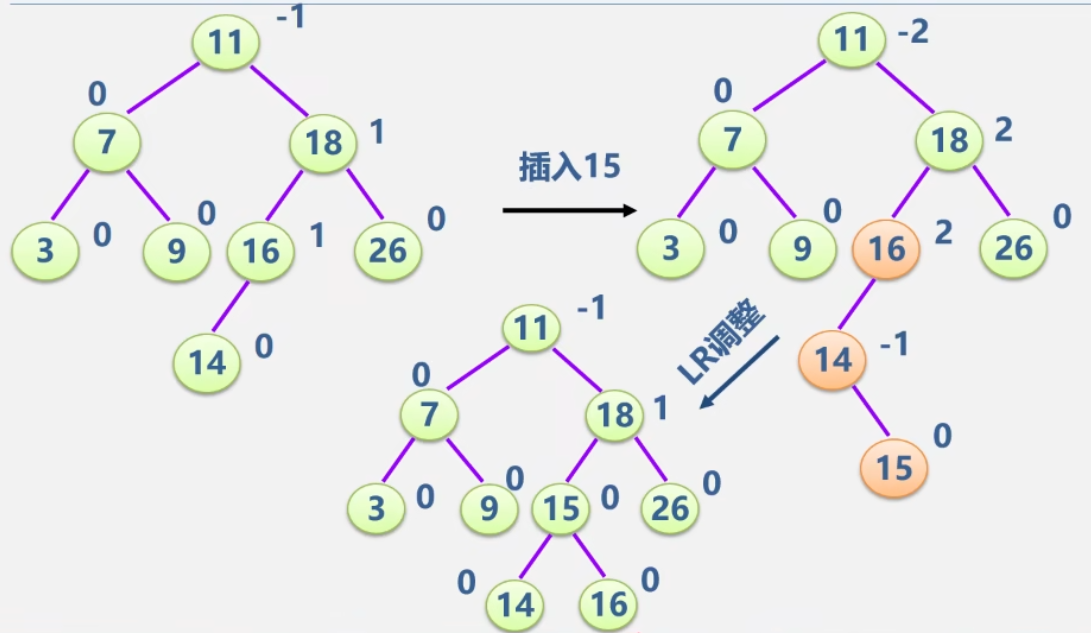
    例：

    输入关键字序列(16，3，7，11，9，26，18，14，15)给出AVL树

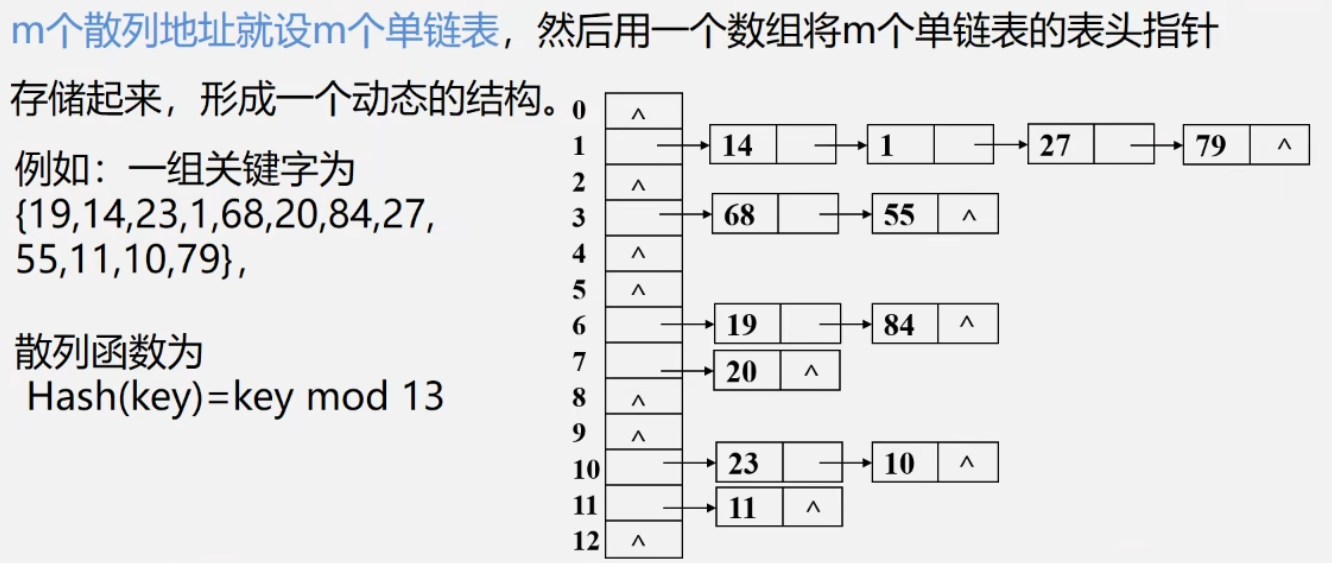
    image

    image

    image

    image

    image

    ​

哈希表的查找

记录的存储位置与关键字之间存在对应关系（hash散列函数）

LOC（i）=H（keyi）

  • 优：查找效率高
  • 缺：空间效率低 （空间换时间）

好的散列表需要好的散列函数+好的冲突方案

  • 所选函数尽可能简单，以便提高转换速度
  • 函数计算出的地址均匀分布，以减少空间浪费

考虑因素：

  • 执行速度（计算散列函数所需时间）
  • 关键字长度
  • 散列表大小
  • 关键字分布
  • 查找频率

散列表的ASL取决于：

  • 散列函数
  • 处理冲突方法
  • 散列表的装填因子α（α=表中填入的记录数/哈希表长）

散列表技术具有很好的平衡性能，优于一些传统技术


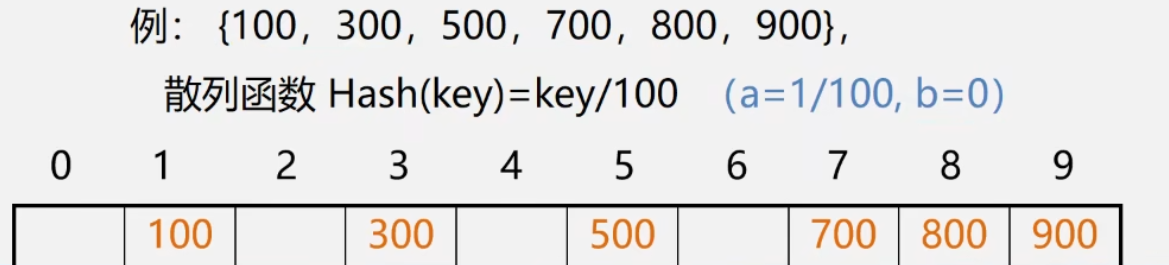
直接定址法

Hash（key）=a*key+b（a,b为常数）

  • 优：以关键码key的某个线性函数值为散列地址，不会产生冲突
  • 缺：要占用连续地址空间，空间效率低

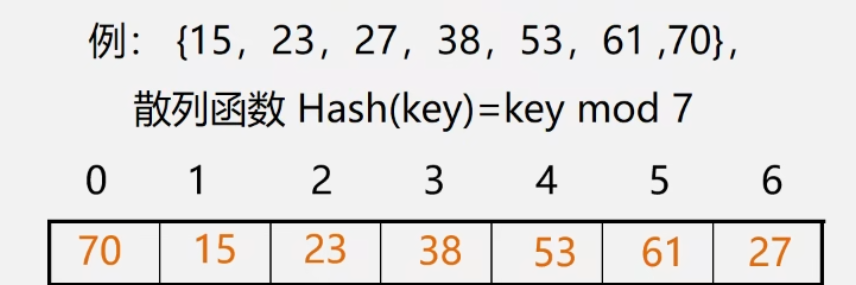
image


除留余数法

除留余数法作散列函数优于其他类型函数

Hash（key）=key mod p（p是个整数）

设表长为m，取p≤m且为质数

image


处理冲突的方法

冲突：不同的关键字映射到同一个散列地址

同义词：具有相同函数值的多个关键字

在散列查找方法中冲突不可能避免，只能尽可能减少


开放定址法（开地址法）

有冲突时就寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将数据元素存入

如：H=（Hash（key）+di）mod p

常用方法：

  • 线性探测法：di为1,2,3,4...等线性序列
  • 二次探测法：di为1^2,- 1^2, 2^2, - 2^2,...二次序列
  • 伪随机探测法：di为伪随机数序列

链地址法（拉链法）

相同散列地址的记录链成一单链表

非同义词不会冲突，无聚集现象；链表上的结点空间动态申请，更适合于表长不确定的情况

优于开放地址法

image

posted @ 2023-02-09 17:28  原语  阅读(149)  评论(0)  编辑  收藏  举报