栈

一种特殊线性表，仅限在一端（栈顶）进行插入和删除操作（通常是表尾）；同线性表相同仍是一对一关系

表尾an端又称为栈顶Top；表头a1端又称为栈底Base；只能在栈顶运算；有顺序栈和链栈

又称为后进先出线性表，简称为LIFO结构

线性表：

Insert（L,i,x)

1<=i<=n+1

Delete(L,i)

1<=i<=n

栈（后进先出，表尾）：

Insert（S,n+1,x）

Delete（S,n）

例：S=(a1栈底,a2,...,an栈顶)

插入元素到栈顶（表尾）成为入栈 push

从栈顶（表尾）删除元素成为出栈 pop

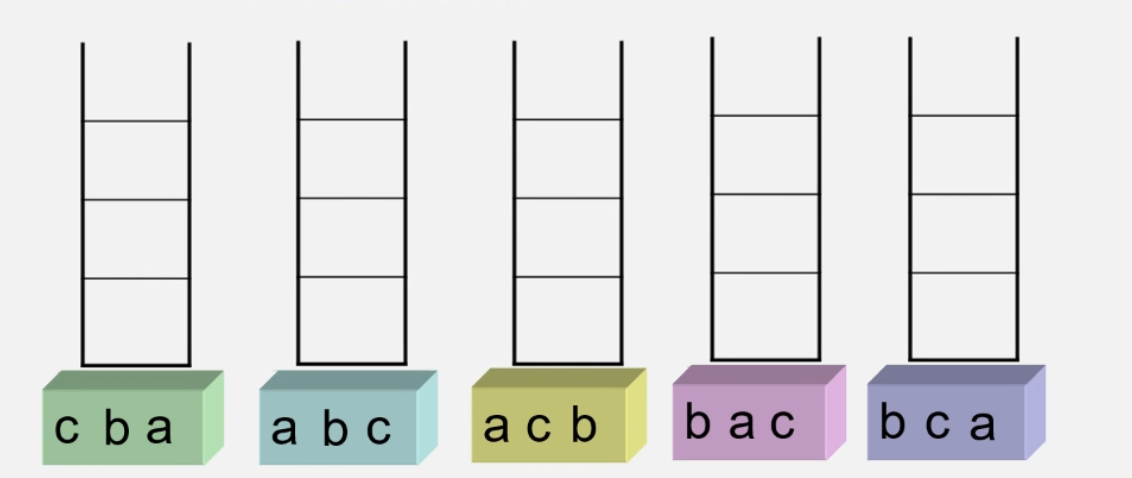
假设有三个元素a,b,c，入栈顺序是a,b,c，则它们的出栈顺序有几种可能？（c,a,b不可能因为全部入栈）

栈的抽象数据类型定义

ADT Stack{

数据对象：D=ai|ai属于Elemset，i=1,2,...,n,n>=0}

数据关系：R1=<ai-1,ai>|ai-1,ai属于D,i=2,3,...,n}

约定an为栈顶，a1为栈底

基本操作：

InitStack(&S)

操作结果：构造一个空栈S

DestroyStack(&S)

初始条件：栈S已存在

操作结果：栈S被销毁

ClearStack(&S)

初始条件：栈S已存在

操作结果：栈S被清空

StackEmpty(S)

初始条件：栈S已存在

操作结果：若为空返回TRUE；否则返回FALSE

StackLength(S)

初始条件：栈S已存在

操作结果：返回S的元素个数，即栈的长度

GetTop(S,&e)

初始条件：栈S已存在且非空

操作结果：用e返回S的栈顶元素

Push(&S,e)

初始条件：栈S已存在

操作结果：插入元素e为新的栈顶元素

Pop(&S,&e)

初始条件：栈S已存在且非空

操作结果：删除S的栈顶元素an，并用e返回其值

}ADT Stack

顺序栈

同一般线性表的顺序存储结构完全相同，利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素

栈底一般在低地址部分

数组作为顺序栈：简单、方便；但易产生溢出

设top指针指向栈顶元素在顺序栈中的位置；但为了操作方便，通常top指针指向栈顶元素之上的下标地址
设base指针指向栈底元素在顺序栈中的位置
设stacksize来表示栈可使用的最大容量

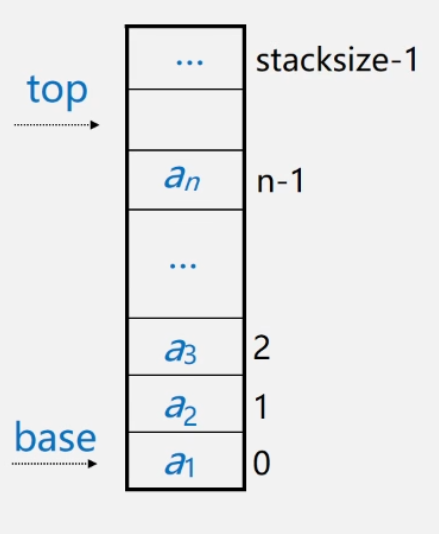
空栈：base==top
栈满top-base==stacksize

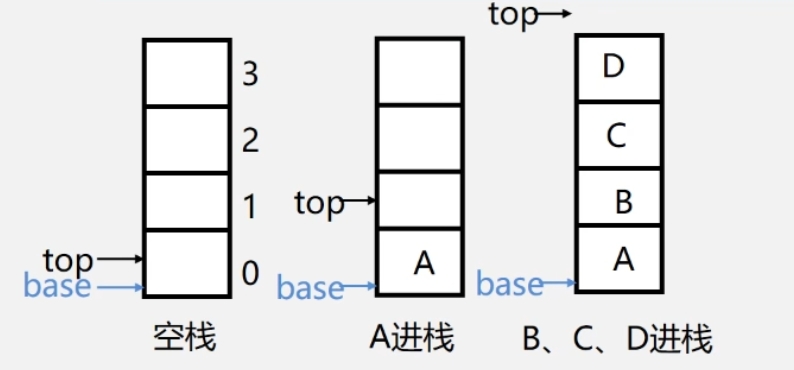
上溢：栈已满，又压入元素，一种错误，使问题无法进行
下溢：栈为空，还弹出元素，一般认为是一种结束条件

顺序栈的定义

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100

typedef struct {
    int *top;
    int *base;
    int stacksize;
}SqStack;

顺序栈的初始化

void InitStack(SqStack *S){
    S->base=(int *)malloc(sizeof(int)*MAXSIZE);
    if(!S->base) printf("Error");
    S->top=S->base;
    S->stacksize=MAXSIZE;
}

顺序栈是否为空

int StackEmpty(SqStack S){
    if(S.top==S.base) return 1;
    else return 0;
}

顺序栈的长度

int StackLength(SqStack S){
    return S.top-S.base;
}

清空顺序栈

void ClearStack(SqStack *S){
    if(S->base) S->top=S->base;
}

顺序栈的销毁

void DestroyStack(SqStack *S){
    if(S->base){
        free(S->base);
        S->stacksize=0;
        S->base=S->top=NULL;
    }
}

顺序栈的入栈

是否栈满
未满则入栈
栈顶指针+1

void Push(SqStack *S,int e){
    if(S->top-S->base==S->stacksize) printf("Error");
    *S->top++=e;        //S.top=e;S.top++;
}

顺序栈的出栈

是否栈空
栈顶指针-1
未空则出栈

void Pop(SqStack *S,int e){
    if(S->top==S->base) printf("Error");
    e=*--S->top;        //    S->top--;e= *(S->top);
}

链栈

链栈是运算受限的单链表，只能在链表头部进行操作

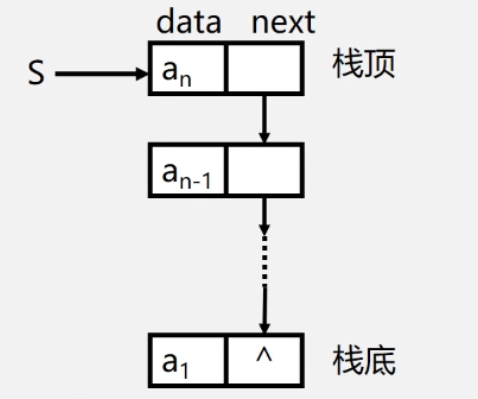
注意链栈中指针的方向

链表的头指针就是栈顶
不需要头结点
基本不存在栈满的情况
空栈就是栈指针指向空：LinkStack S;S=NULL;
插入和删除仅在栈顶执行

链栈的定义

typedef struct Stacknode{
    int data;
    struct Stacknode *next;
}StackNode,*LinkStack;

链栈的初始化

void InitStack(LinkStack S){
    S=NULL;
}

链栈是否为空

int StackEmpty(LinkStack S){
    if(S==NULL) return 1;
    else return 0;
}

链栈的入栈

void PushStack(LinkStack S,int e){
    LinkStack p=malloc(sizeof(StackNode)*MAXSIZE);
    p->data=e;
    p->next=S;
    S=p;
}

链栈的出栈

void Pop(LinkStack S,int e){
    LinkStack p=malloc(sizeof(StackNode)*MAXSIZE);
   e=S->data;
   p=S;
   S=S->next;
   free(p);
}

链栈的取栈顶元素

int GetTop(LinkStack S){
    if(S!=NULL) return S->data;
}

栈的应用

数制转换（取余）

例：把十进制数159转化为八进制数
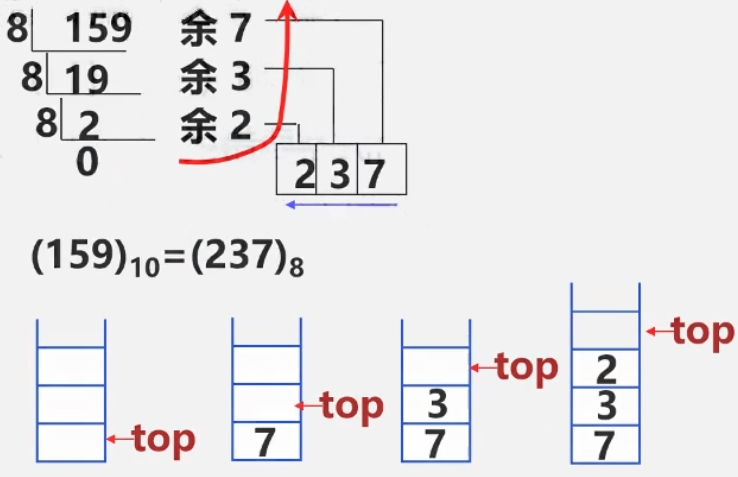
括号匹配：左括号进栈，右括号看栈顶是否与之匹配；若匹配则出栈，不匹配则验证失败

先入栈的后匹配，后入栈的先匹配

例：
- ( [] () ) 或 [ ( [ ] [ ] ) ] √
- [ ( ] ) ×
- ( [ ( ) ）或 ( ( ) ] ) ×
行编辑程序
迷宫求解
表达式求值：

表达式的组成：
- 操作数：常数、变量
- 运算符：算术、关系、逻辑运算符
- 界限符：左右括号、表达式结束符
- 算符栈OPTR：用于寄存运算符
- 操作数栈OPND：用于寄存运算数和运算结果
从左至右扫描表达式的每个字符直到遇到结束符：
- 扫描到运算数：压入OPND栈
- 扫描到运算符：
  - 若该运算符比OPTR栈顶的运算符优先级高，则压入OPTR栈，继续向后处理
  - 若该运算符比OPTR栈顶的运算符优先级低，从OPND栈中弹出两个运算数，从OPTR中弹出栈顶运算符进行运算，并将结果压入OPND栈
八皇后问题
函数调用:
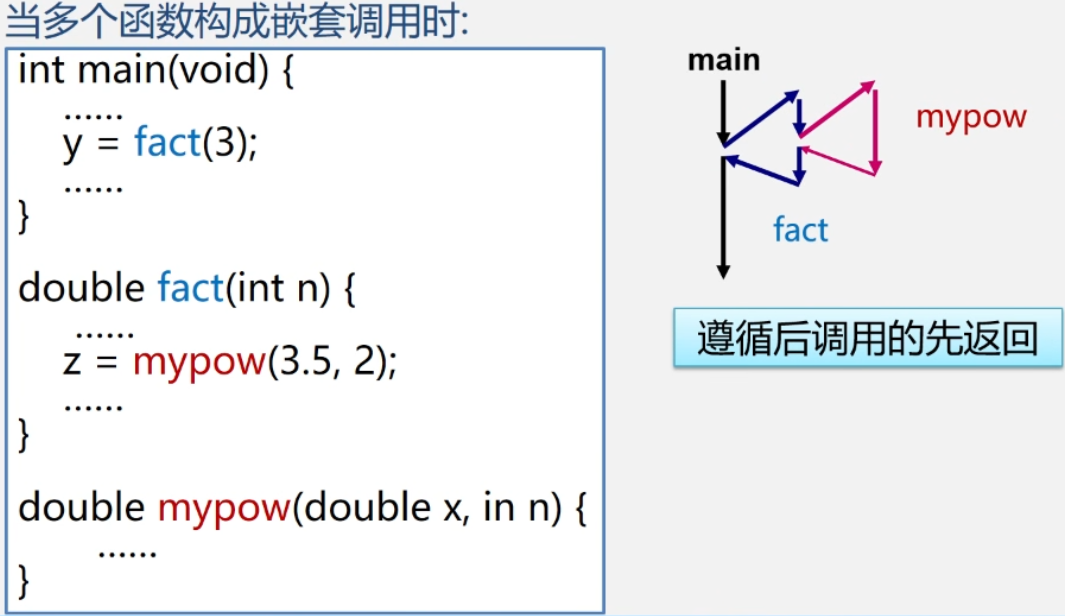
递归调用：

递归：若一个对象部分的包含自己，或用自己给自己定义

优：结构清晰，程序易读

缺：每次调用都要生成工作记录，保存状态信息入栈(递归工作栈);返回时要出栈恢复状态信息，时间开销大

递归->非递归：
- 尾递归、单向递归->循环结构
- 自用栈模拟系统的运行时栈
一般形式：
```
void p(参数表){
  if(递归结束条件) 可直接求解;   //基本项
  else p(较小的参数);   		  //归纳项 
}
```
- 递归定义的数学函数
  - 阶乘：
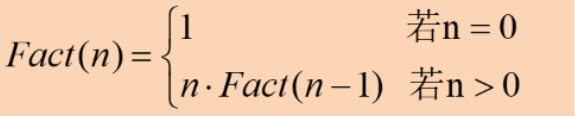
  - 斐波那契：
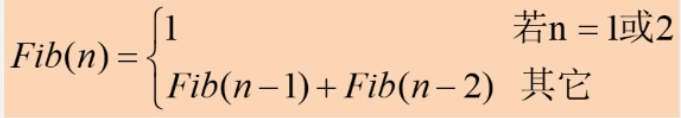
- 具有递归特性的数据结构：二叉树、广义表
- 可递归求解的问题：迷宫问题、汉诺塔问题