线性表的顺序存储
线性表的顺序存储
线性表的顺序表示又称为顺序存储结构或顺序映像
顺序存储:把逻辑上相邻的数据元素(类型相同)存储在物理上相邻(中间没有空出存储单元,占用一片连续的存储空间)的存储单元中的存储结构;逻辑位序与物理位序相差1
- 优:
- 任一元素可以随机存取
- 存储密度大
- 缺:
- 属于静态存储形式,元素个数不能自由扩充
- 插入、删除某一元素时需要移动大量元素
- 浪费存储空间
(a1 , a2 , a3 , ... , ai-1 , ai , ai+1 , ... ,an)
n为元素个数即表长,当n=0时为空表
线性表的第一个元素a1的存储位置成为线性表的起始地址或基地址
假设线性表的每个元素需要占用l个存储单元,则元素的存储位置满足:LOC(ai)=LOC(a1)+(i-1)l
例:26个英文字母组成的英文表
(A , B , C , ... , Z)
元素都是字母,元素间是线性关系(有一个前驱、一个后继,都是一对一的)
一元多项式的计算:
线性表R=(p0+q0,p1+q1,p2+q2,p3+q3,...,pm+qm,pm+1 + qm+1)
稀疏多项式的计算:线性表P=((p1,e1),(p2,e2),(p3,e3),..., (pm,em))
例:
A(x)=7+ 3x+9x^8 +5x^17 B(x)=8x+22x^7 -9x^8
| 下标i | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 系数a[i] | 7 | 3 | 9 | 5 |
| 指数 | 0 | 1 | 8 | 7 |
| 下标i | 0 | 1 | 2 |
|---|---|---|---|
| 系数b[i] | 8 | 22 | -9 |
| 指数 | 1 | 7 | 8 |
线性表A=((7,0),(3,1),(9,8),(5,7))
线性表B=((8,1),(22,7),(-9,8))
创建一个新的数组C,分别重头遍历A、B的每一项:若指数相同则和相加不为0就在C中添新项;指数不同将指数较小的项赋值到C中 ;一个多项式已遍历完毕,将另一个依次复制到C中即可
顺序表顺序存储结构定义
#define MAXSIZE 1000
typedef struct{
float p; //系数
int e; //指数
} Polynomial;
typedef struct {
Polynomial *elem; //存储空间的基地址
int length; //多项式中当前项的个数
}SqList;
用一维数组名表示顺序表,但线性表长可变,数组长度不可动态定义;因此可以用一变量表示顺序表的长度属性
数组静态分配:
#define List_Size 100 //线性表存储空间的初始分配量
typedef struct{
int elem[List_Size];
int lenth; //当前长度
} SqList;
数组动态分配:用malloc动态分配空间
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100 //线性表存储空间的初始分配量
typedef struct {
int *elem;
int length;
}SqList;
int main(void)
{
SqList L;
L.elem=(int *)malloc(sizeof(int)*MAXSIZE);
free(L.elem);
}
线性表顺序存储的初始化
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef struct{
int *elem;
int length;
} SqList;
int InitList_Sq(SqList *L){ //构造一个空的顺序表
L->elem=(int *)malloc(sizeof(int)*MAXSIZE); //为顺序表分配空间
if(!L->elem) printf("failed"); //存储分配失败
L->length=0; //表长为0
return 1;
}
int main(void)
{
SqList L;
InitList_Sq(&L);
printf("successful");
free(L.elem);
}
线性表顺序存储的销毁
void DestroyList(SqList *L){
if(L->elem){
free(L->elem); //释放存储空间
}
}
线性表顺序存储的清空
void ClearList(SqList *L){
L->length=0; //线性表长置0
}
获取线性表顺序存储的长度
int GetLength(SqList L){
return L.length;
}
判断线性表是否为空
int IsEmpty(SqList L){
if(L.length==0){
return 1;
}
else return 0;
}
线性表顺序存储的取值(随机存取)
int GetElem(SqList L,int i,int *e){
if(i<1||i>L.length) return 0; //判断i值是否合理
e=L.elem[i-1]; //第i-1单元存着第i个元素
return 1;
}
线性表顺序存储的按值查找
int LocateElem(SqList L,int e){
for (int i = 0; i <L.length ; i++) {
if(L.elem[i]==e){
return i+1;
}
}
return 0;
}
其基本语句执行次数与输入有关;平均时间复杂度O(n)
平均查找长度ASL:为确定记录在表中的位置,需要与给定值进行比较的关键字的个数的期望值
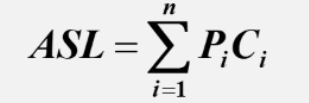
线性表顺序存储的插入
- 插入在最后
- 插入在中间
- 插入在最前
- 判断插入位置是否合法;存储空间是否已满
int ListInsert_Sq(SqList *L,int i,int e){
if(i<1||i>L->length+1){
return 0;
}
if(L->length==MAXSIZE){
return 0;
}
for (int j = L->length-1; j >=i-1 ; j--) {
L->elem[j+1]=L->elem[j];
}
L->elem[i-1]=e;
L->length++;
}
平均时间复杂度O(n)
线性表顺序存储的删除元素
int ListDelete_Sq(SqList *L,int i){
if(i<1||i>L->length) return 0;
for (int j = i; j <L->length ; j++) {
L->elem[j-1]=L->elem[j];
}
L->length--;
return 1;
}
平均时间复杂度O(n)
线性表顺序存储的合并
两个多项式的相加
- 创建一个空表Lc
- 依次从La或Lb中摘取元素值较小的结点插入到Lc表最后,直至一个表变为空
- 继续将剩余表中的结点插入到Lc表最后
#include <stdio.h>
#include <stdlib.h>
typedef struct{
int *elem;
int length;
}SqList;
void MergeList_Sq(SqList *La,SqList *Lb,SqList *Lc){
int *pa,*pb,*pc;
pa= (int *) &La->elem;
pb= (int *) &Lb->elem;
pc= (int *) &Lc->elem;
Lc->length=La->length+Lb->length;
Lc->elem=(int *)malloc(sizeof(int)); //为合并后的新表分配一个空间
SqList *La_last= (SqList *) (La->elem + La->length - 1);//指针La_last指向La表中最后一个元素
SqList *Lb_last= (SqList *) (Lb->elem + Lb->length - 1);//指针Lb_last指向Lb表中最后一个元素
while (pa<=(int *)La_last&&pb<=(int *)Lb_last){ //两个表非空
if(*pa <= *pb){
*pc++=*pa++;
}else{
*pc++=*pb++;
}
}
while (pa<=(int *)La_last) *pc++=*pa++;//Lb表已到表尾,将Lb表剩余元素加入Lc表
while (pb<=(int *)Lb_last) *pc++=*pb++;//La表已到表尾,将La表剩余元素加入Lc表
}
int main(void)
{
}
时间复杂度是O(La.length+Lb.length)


