编译原理
编译原理
编译阶段
词法 分析—>语法 分析（核心）—>语义 分析(数组下标越界/运算符与运算对象类型不匹配)和中间代码生成 —>代码优化 （运行时间短且占用存储空间小：局部优化/循环优化/全局优化）遵循语义规则 —>目标代码生成（依赖于具体的计算机的硬件系统结构和指令系统） 及表格处理 和出错处理
对说明语句进行翻译
翻译：编译/解释
编译方式与解释方式的根本区别在于是否生成目标代码
解释程序（属于编译程序）处理语言时,大多数采用的是先将源程序转化为中间代码，在解释执行
面向机器语言指的是：特定计算机系统所固定的语言
对编译程序（系统软件）而言，输入的数据是源程序 ，输出的结果是目标程序 ,是对高级语言的翻译
编译程序生成的目标代码程序必须经过链接装配是可执行的程序
经过编译所得到的目标程序是机器语言或汇编语言程序
编译程序的各个阶段都涉及表格管理
文法与符号串
文法
G[s] =(Vn,Vt,P,S) /非终结符、终结符、产生式、开始符号
语言：句子的集合：文法G产生的句子的全体叫做语言
一个文法所描述的语言是唯一的，描述一个语言的文法是不唯一的
产生正规式的文法是3型文法
文法符号有综合属性和继承属性
BNF是一种广泛采用的描述文法的工具
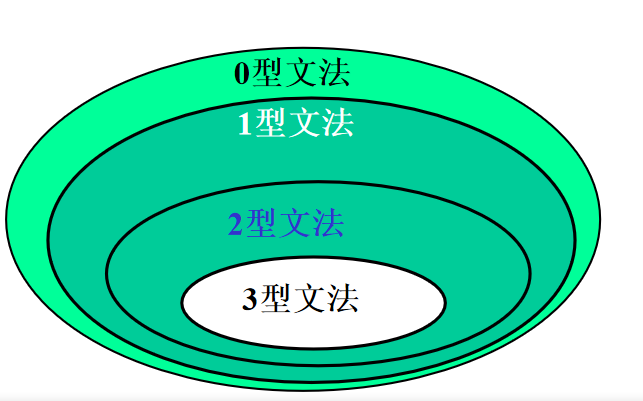
文法按产生式的形式分为四种类型：
- 0型文法，又称短语文法
- 1型文法，又称上下文有关文法
- 2型文法，又称上下文无关文法
- 3型文法，又称正规文法
右线性文法(正规文法/3型文法) ：产生式右部VN在VT的右边 例：A->aB A->a
符号串
字母表∑中的符号组成的任何有穷序列
ε是∑上的符号串
符号串中的符号排列是有顺序的
词法分析
词法分析应遵循构词规则
一个名字的属性包括类型和作用域
扫描器是词法分析，它接收输入的源程序 ，对源程序进行词法分析并识别出一个个单词符号供语法分析器使用
扫描器所完成的任务是从字符串形式的源程序中识别出一个个具有独立含义的最小语法单位即单词
识别的单词个数不包括数字
词法分析生成器（lex）的输出结果是单词的种别编码和自身值
源程序中的单词是具有独立意义的最小语法单位
正规式：将文法的终结符号用 * . |连接组成的表达式
一个正规语言只能对应一个最小有限状态自动机
自动机：
-
NFA：多个初态，若干终态，可以有标识为ε的边，可能有零条、一条甚至多条
-
DFA：一个初态，若干终态，每个状态都有且只有一条关于这个符号的出边，转换箭头上的标签必须是字母表中的
NFA->DFA:
-
确定化：求ε-CLOSURE（S）
-
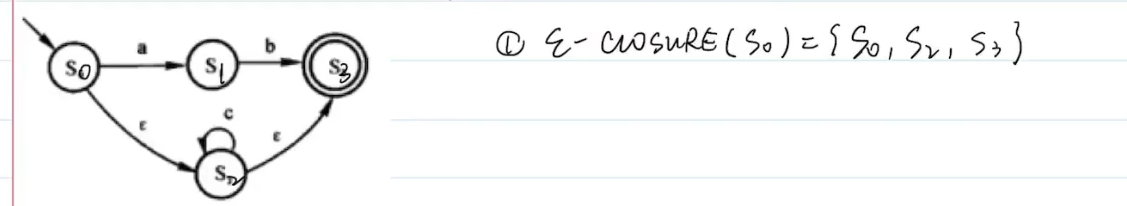
画表
-
最小化 π={{其他集}，{含终态集}}（合并成角标最小）
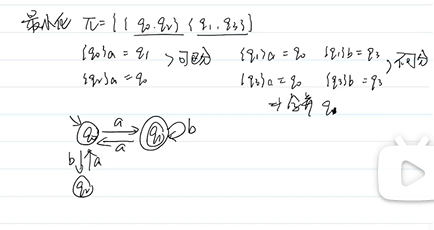
正规式构造DFA：
-
先构造NFA
-
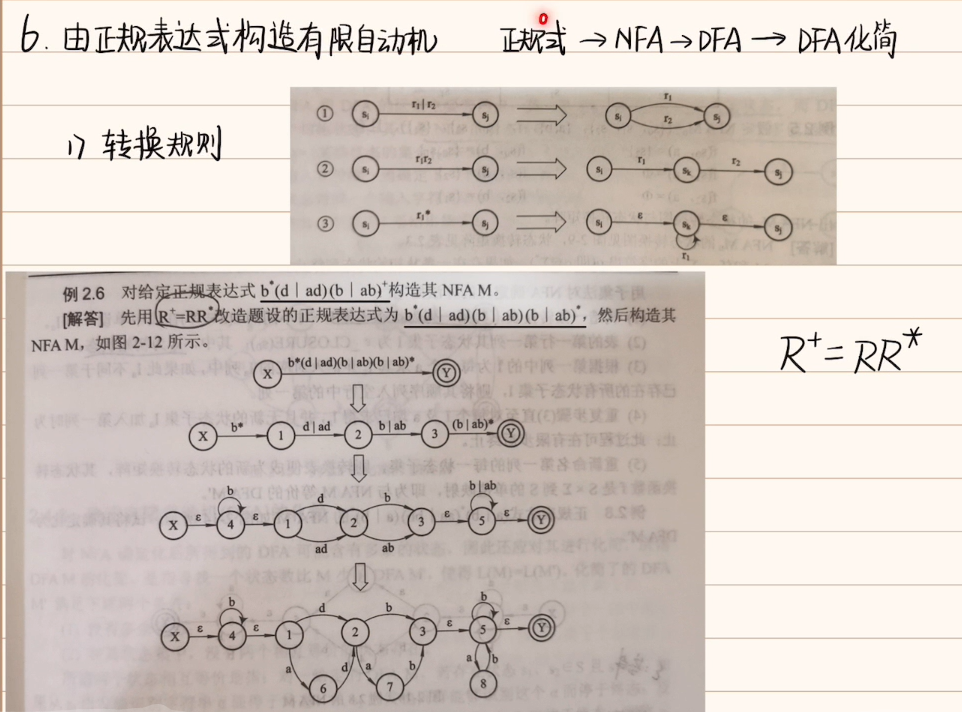
NFA构造DFA
语法分析
语法分析器输入的是单词符号输出的是语法单位
else没有匹配的if/使用的函数没有定义/在数中出现非数字字符
上： 分析树的根节点或文法开始符号
下： 被分析的源程序串
自顶向下（推导）从文法产生语言的角度
最左推导： 用产生式的右部替换产生式的左部分析器是自左向右扫描，采用最左推导
最右推导（规范推导）
自底向上（规约）从自动机识别语言的角度
最左规约（规范规约/规约）
最右规约 ：推导的逆过程
语法分析树
任何语法结构都可以用抽象语法树来表示
若无二义性则最左推导和最右推导对应的语法树必定相同
二义性文法：L(G)的某个句子对应不止一个最左/最右推导
短语：每棵子树的叶子 （从下往上看）
直接短语：每棵直接子树（高度为1的树）的叶子
句柄：某句型的最左直接短语（最先被规约的子串） （从下往上看/同一高度）
素短语：至少包含一个终结符且不包含更小素短语的短语
自顶向下（消除回溯）
LL(1)：第一个“L”表示从左向右扫描输入，第二个“L”表示产生最左推导，而“1”表示在每一步中只需要向前看一个输入符号来决定语法分析动作
一个右线性文法G一定是LL（1）文法
每一个文法都可以改成LL(1)文法
消除左递归
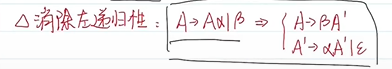
判断LL（1）文法
对于文法LL(1)文法G，当且仅当G的任意两个不同产生式 A -> α | β
- 不存在左递归（不存在终结符号a使得α和β都能推导出以a开头的串）
- α和β中最多只有一个可以推导出空串
- SELECT（A->α）∩ SELECT（A->β）=∅
LL（1）分析表
递归向下
预测分析
自底向上（寻找句柄）
简单优先： 所有符号（终结符和非终结符）之间的优先关系(相邻有序符号间谁先归约) 相邻性与有序性
优先关系：
- X=Y 文法G中存在产生式A→...XY...
- X<Y 文法G中存在产生式A→...XB...，且B-+>Y...
- X>Y 文法G中存在产生式A→...BD...，且B-+>...X,D-*>Y...
满足条件：
- 在文法符号集V中，任意两个符号之间(有序)最多只有一种优先关系成立
- 在文法中任意两个产生式没有相同的右部
- 不含空产生式
算符优先： 只规定算符（终结符）之间的优先关系，每次都是对句柄 进行规约以最左素短语作为每一步归约的对象，特别适用于表达式的分析（不是一种规范归约法）
如果不含空产生式的上下文无关文法 G 中没有形如 U…VW…的产生式，其中V,W∈VN则称G 为算符文法
在算符文法中任何句型都不包含两个相邻的非终结符
无二义的
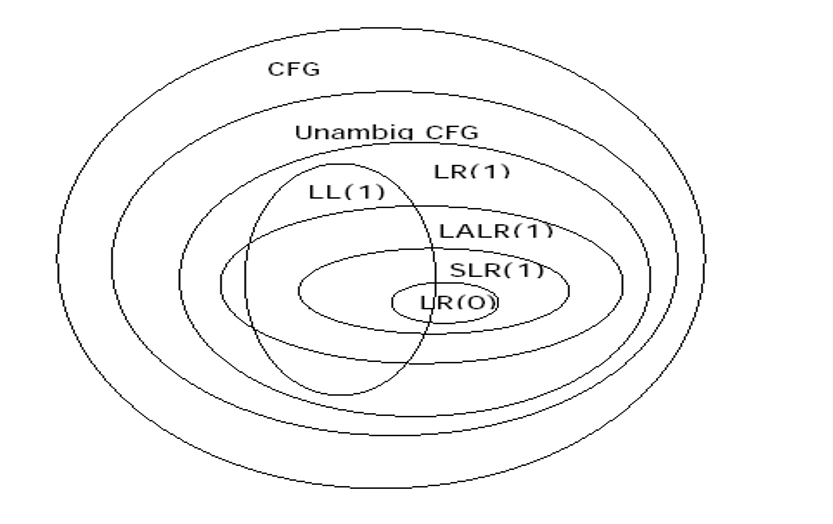
LR分析(无二义性)：（层次包含关系）LR(0)<SLR(1)<LALR(1)<LR(1)
无二义性：最左推导和最右推导对应的语法树必定相同
LR(0)项目： 右部带·的产生式
S’→S·（接受项目）
S→α·（规约项目）
A->α·xβ(移进项目：·后为VT)
A->α·Xβ(待约项目：·后为VN)
判断LR（0）文法：
无冲突项目（移进-规约冲突、规约-规约冲突）:
LR（0）分析表：
-
拓广文法
-
识别全部活前缀的DFA
-
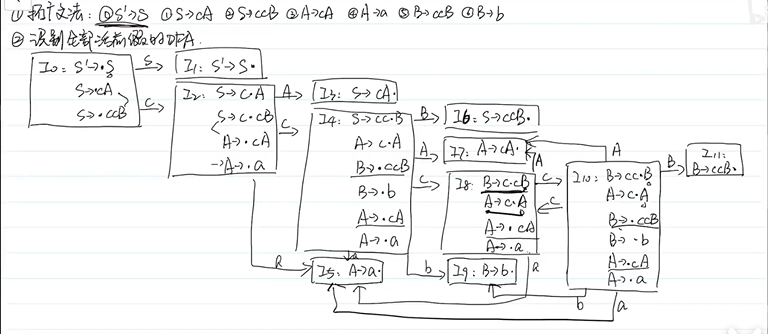
构造分析表
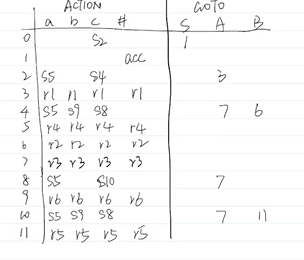
判断SLR（1）文法：
- DFA中有冲突项目（移进-规约冲突，规约-规约冲突）
- 移进项目∩该产生式左部FOLLOW集为∅
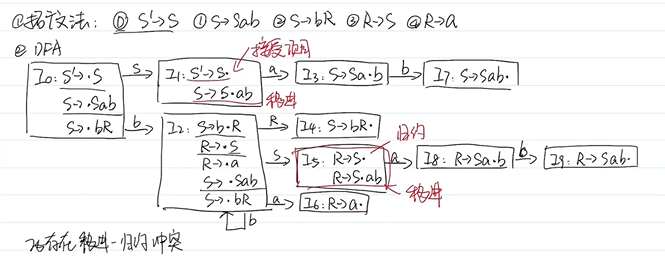
SLR（1）分析表对每个规约项目A->α,求FOLLOW(A)得到的输入符号出填rn,其余与LR（0）分析表一样
判断LR（1）文法：
构造带向前搜索符的DFA,无规约-规约冲突
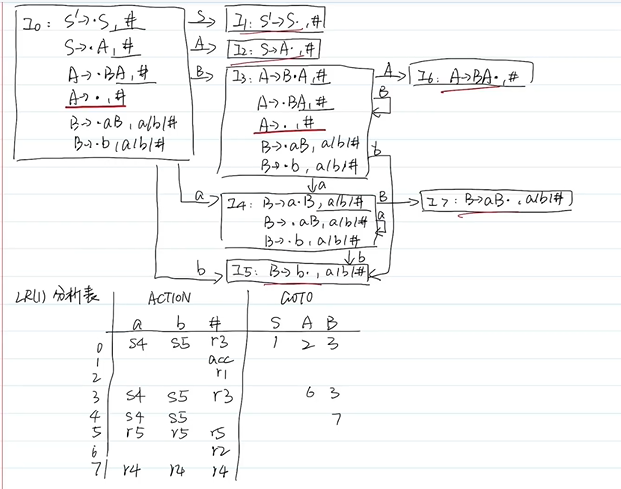
判断LALR（1）文法：
LR（1）文法合并同心集后无规约-规约冲突，核相同，向前搜索符不同 (取并集)
FIRST集
若X是VT则FIRST(X)={X}
若X是VN且X->Y1...YK∈P（K>=1）则FIRST(X)={Y1}
若X是VN且X->Y1...YK∈P（K>=1）若Y1->*ε 则FIRST(X)=FIRST(Y1)∪FIRST(Y2)
若X是VN且X->Y1...YK∈P（K>=1）若Y1...YK->*ε 则将ε加入FIRST(X)
例：计算X的FIRST(X)
- E->TE' FIRST(E)=FIRST(T)==
- E'->+TE'|ε FIRST(E')=
- T->FT' FIRST(T)=FIRST(F)=
- T'->*FT'|ε FIRST(T')=
- F->(E)|id FIRST(F)=
FOLLOW集
找产生式右部的非终结符，若后面为VT则写入FOLLOW集，若后面为空写左部的follow集，若后面为VN则写入VN的FIRST集中非空元素
例：计算A的FOLLOW(A)
- E->TE' FOLLOW(E)=
- E'->+TE'|ε FOLLOW(E')=FOLLOW(E)=
- T->FT' FOLLOW(T)=
- T'->*FT'|ε FOLLOW(T')=
- F->(E)|id FOLLOW(F)=
SELECT集
A->α
若α不能推出ε，则SELECT（A->α） = first（α）
若α能推出ε，则select（A->α）= follow(A)
逆波兰式（后缀）
- 运算对象顺序相同
- 运算符紧跟运算对象后
- 转移操作符：
- P BR：无条件跳转到P
- e' P BZ:e'为假时转移到P
- e1' e2' P BL:e1'<e2'时转移到P
算术运算符高于关系运算符高于逻辑运算符
中间代码生成
四元式（操作符、左操作数、右操作数、结果）
三元式之间的联系是通过指示器实现的 ，优点：采用间接码表，便于优化处理（三元式不易改变，易于改变的是间接码表）
四元式之间的联系是通过临时变量实现的，优点：便于优化处理及表的更动
树形表示和三元式不便于优化，四元式和间接三元式便于优化
用语义规则可以把a:=b+c翻译成四元式
布尔表达式到四元式：
-
（jnz,A1,-,P）：当A1为真时，跳到四元式P
-
（jrop,A1,A2,P）:当A1 rop A2成立时，跳到P
-
（j,-,-,P）:无条件跳转到P
中间代码生成
- 局部优化
- 循环优化
- 全局优化
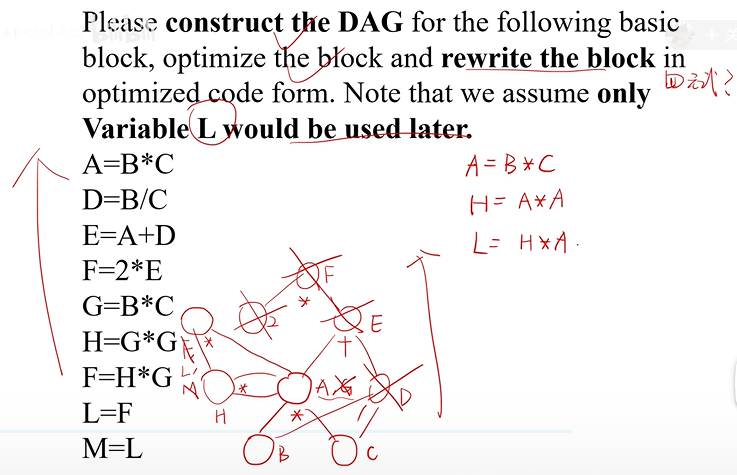
DAG(有向无环图)优化：
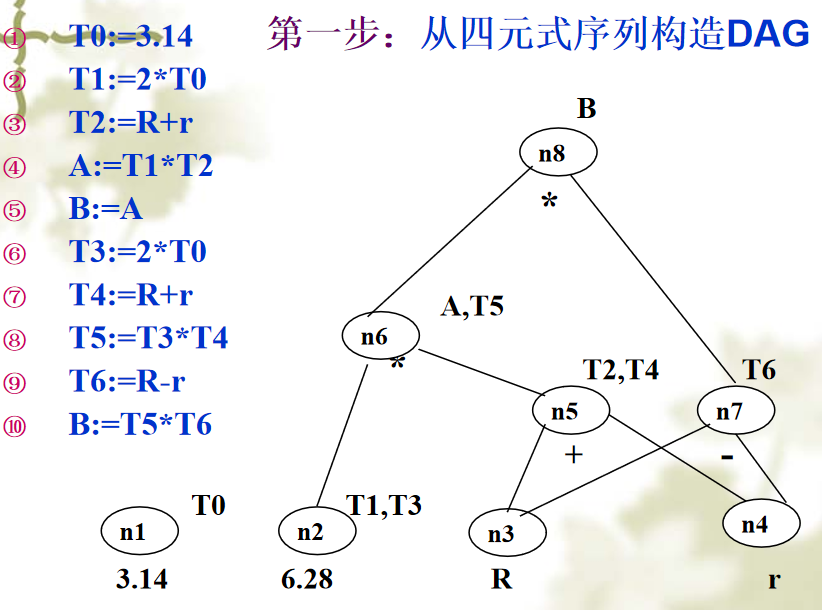
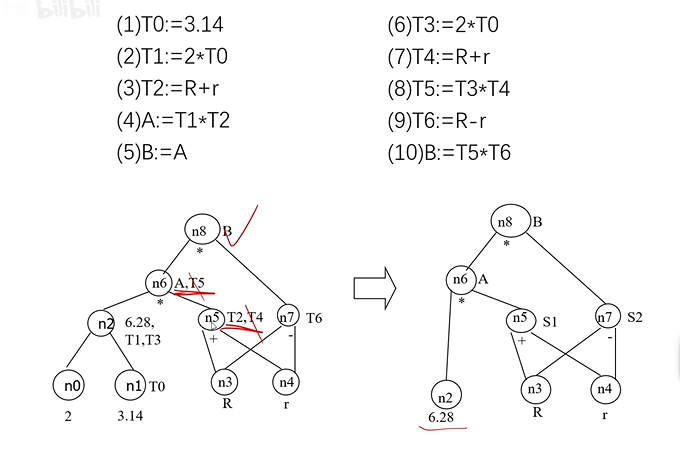
优化：
- 一个节点只能代表一个字母
- 迭代删除后续程序没有使用的变量的根节点（新出现两个根节点）
- 经过两个常量运算得到的常量直接算出，并删除两个子节点
