斐波那契【性质总结】

斐波那契的一些性质在竞赛中会出现，作为较简单的签到题，但是如果不知道的话，就很难做出来。刻意的记一下是很重要的。

递推式：F【i】 = F【i - 1】 + F【i - 2】

1.连续三项，首尾两项积等于中间一项平方和 + 1，即：F【i】 * F【i + 2】 = F【i + 1】* F【i + 1】 + 1。

2.前 n 项和，等于第 n + 2项 - 1，即：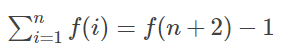

 

 3.前n个奇数项的和等于第2n项。

4.前n个偶数项的和等于第2*n+1项 - 1。（0不算第一个偶数项）

5.相邻两项的平方差等于这两项前后两项的积。即：F【i】 *  F【i】- F【i - 1】 * F【i - 1】 = F【i + 1】 * F【i - 2】。

6.