马拉车算法,mannacher查找最长回文子串

作用：

在线性时间内找到一个字符串的最大回文子串

原理：

奇偶变换：为处理字符串方便，现将给定的任意字符串进行处理，使所有可能的奇数/偶数长度的回文子串都转换成了奇数长度。

具体就是在每个字符的两边都插入一个特殊的符号。比如hhjj变成 #h#h#j#j#， aba变成 #a#b#a#；

为防止数组越界，可以在字符串的开始加入另一个特殊字符，比如“?#a#b#a#?” 。

定义一个辅助数组int p[]，p[i]表示以s_new[i]为中心的最长回文的半径，例如：

可以看出，p[i]-1正好是原字符串中最长回文串的长度。
Manacher 算法之所以快，就快在对 p 数组的求法上有个捷径。

 

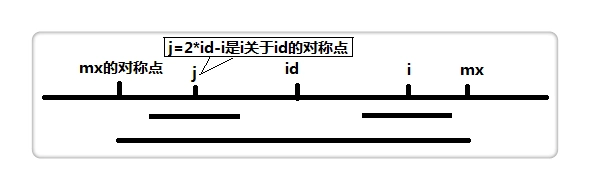
 2 * id - i 为 i 关于 id 的对称点，即上图的 j 点，而 p[j]表示以 j 为中心的最长回文半径，因此我们可以利用 p[j] 来加快查找。

if(i < mx)//mx为以id为中心的最远扩展回文串的右边界,i为扫描到的点 
{
	p[i] = min(p[2 * id - i], mx - i);
}

　　注解在代码里,例题链接：http://acm.hdu.edu.cn/showproblem.php?pid=3068

#include<stdio.h>
#include<string.h>
#include<algorithm>
#define mem(a, b) memset(a, b, sizeof(a))
using namespace std;

char str[110010];
char new_s[110010 * 2]; //mannacher数组因为奇偶变换加了符号进去,数组要开原字符串2倍大小 
int p[110010 * 2];

void get_news(int len)//构造新字符串 
{
	new_s[0] = '^';
	new_s[1] = '#';
	int j = 1;
	for(int i = 0; i < len; i ++)
	{
		new_s[++ j] = str[i];
		new_s[++ j] = '#';
	}
	j ++;
	new_s[j] = '\0';
}

int mannacher(int len)
{
	mem(p, 0);
	int mx = 0;
	int id = 0;
	int maxlen = -1;//答案,最长字符串长度初始化 
	for(int i = 1; i < len; i ++)
	{
		if(i < mx)//mx为以id为中心的最远扩展回文串的右边界,i为扫描到的点 
		{
			p[i] = min(p[2 * id - i], mx - i);//需搞清楚上面那张图含义, mx和2*id-i的含义
		}
		else   //i >= mx 不能利用对称性来直接求解p[i]了, 所以先p[i] = 1,然后暴力更新 
			p[i] = 1;
		while(new_s[i - p[i]] == new_s[i + p[i]])//不需边界判断，因为左有'^',右有'\0' 
			p[i] ++;
		if(mx < i + p[i])//每走一步i，都要和mx比较，我们希望mx尽可能的远，这样才能更有机会执行if (i < mx)这句代码，从而提高效率 
		{
			id = i;
			mx = i + p[i];
		}
		maxlen = max(maxlen, p[i] - 1);
	}
	return maxlen;
}

int main()
{
	while(scanf("%s", str)!=EOF)
	{
		int len = strlen(str);
		get_news(len);
		len = strlen(new_s);
		int ans = mannacher(len);
		printf("%d\n", ans);
	}
	return 0;
}