动态规划基础

动态规划基础

在写这篇博客之前，我被动态规划之类的问题折磨地"遍体鳞伤" 。直到我了解到了闫氏DP分析法。之后，我吃饭更香了，身体更棒了!!!

......

咳嗯额...开个玩笑，言归正传。

闫氏DP分析法是从集合地角度来分析求解DP问题的。它的具体思想是：找某个依据将某个状态用它的子状态来不重不漏的表示出来，即对这个状态的集合做一个划分，这里的划分犹如离散数学中集合划分--不重不漏！！！然后我们对所有子状态的求解(求最大、最小、累加)就是等效地对原状态求解。

这个集合呢，有一个属性，Max/Min/Count.这就要具体问题具体分析，比如题意，求某某某最大值、最小值、方案数......

言语难以诠释真理...下面我们拿几个例子为例：

题目1、描述：Hello Kitty想摘点花生送给她喜欢的米老鼠。

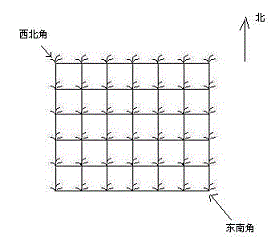
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围

1≤T≤100 1≤R,C≤100 0≤M≤1000

输入样例：

 2
 2 2
 1 1
 3 4
 2 3
 2 3 4
 1 6 5

输出样例：

 8
 16

 

分析图：

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int N = 110;
 int a[N][N];
 int f[N][N];
 int T;
 int r,c;
  
 int main(){
     cin>>T;
     while(T--){
         cin>>r>>c;
         for(int i=1;i<=r;i++){
             for(int j=1;j<=c;j++){
                 scanf("%d",&a[i][j]);
             }
         }//读入数据
         //状态转移:朴素dp，几维就有几层循环
         for(int i=1;i<=r;i++){
             for(int j=1;j<=c;j++){
                 f[i][j] = max(f[i-1][j] , f[i][j-1])+a[i][j];
             }
         } 
         cout<<f[r][c]<<endl;
     }   
     return 0;
 }

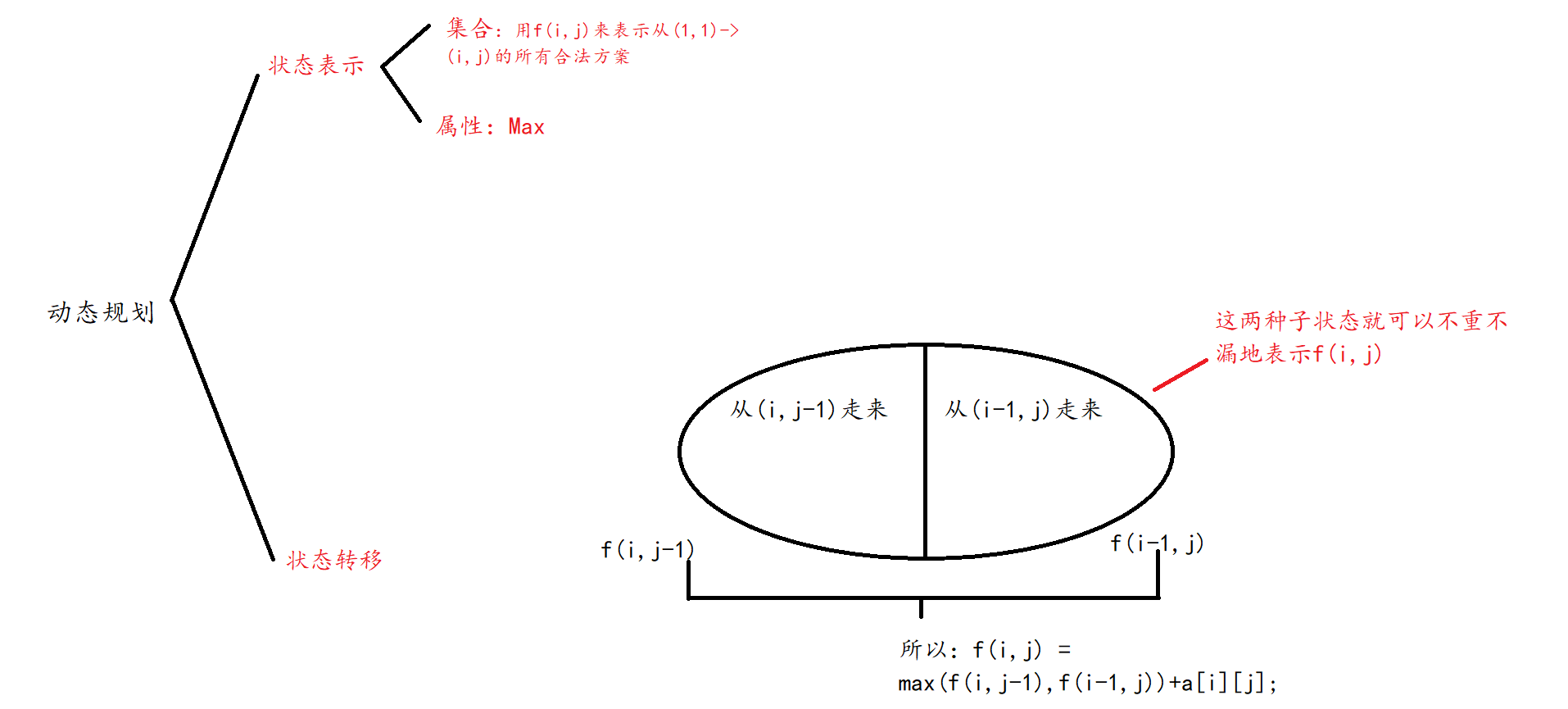
题目2、描述：给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式

第一行包含整数N。

第二行包含N个整数，表示完整序列。

输出格式

输出一个整数，表示最大长度。

数据范围

1≤N≤1000 −10^9≤数列中的数≤10^9

输入样例：

 7
 3 1 2 1 8 5 6

输出样例：

 4

分析图：

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 using namespace std;
 const int N = 1010;
 int a[N],f[N];
 int n;
 int main(){
     cin>>n;
     for(int i=1;i<=n;i++){
         f[i]=1;
         scanf("%d",&a[i]);
     }
     
     int mx = 1;
     for(int i=1;i<=n;i++){
         for(int j=1;j<i;j++){
             if(a[i]<=a[j])continue;
             f[i] = max(f[i],f[j]+1);
         }
         mx = max(mx,f[i]);
     }
     
     cout<<mx<<endl;
     return 0;
 }

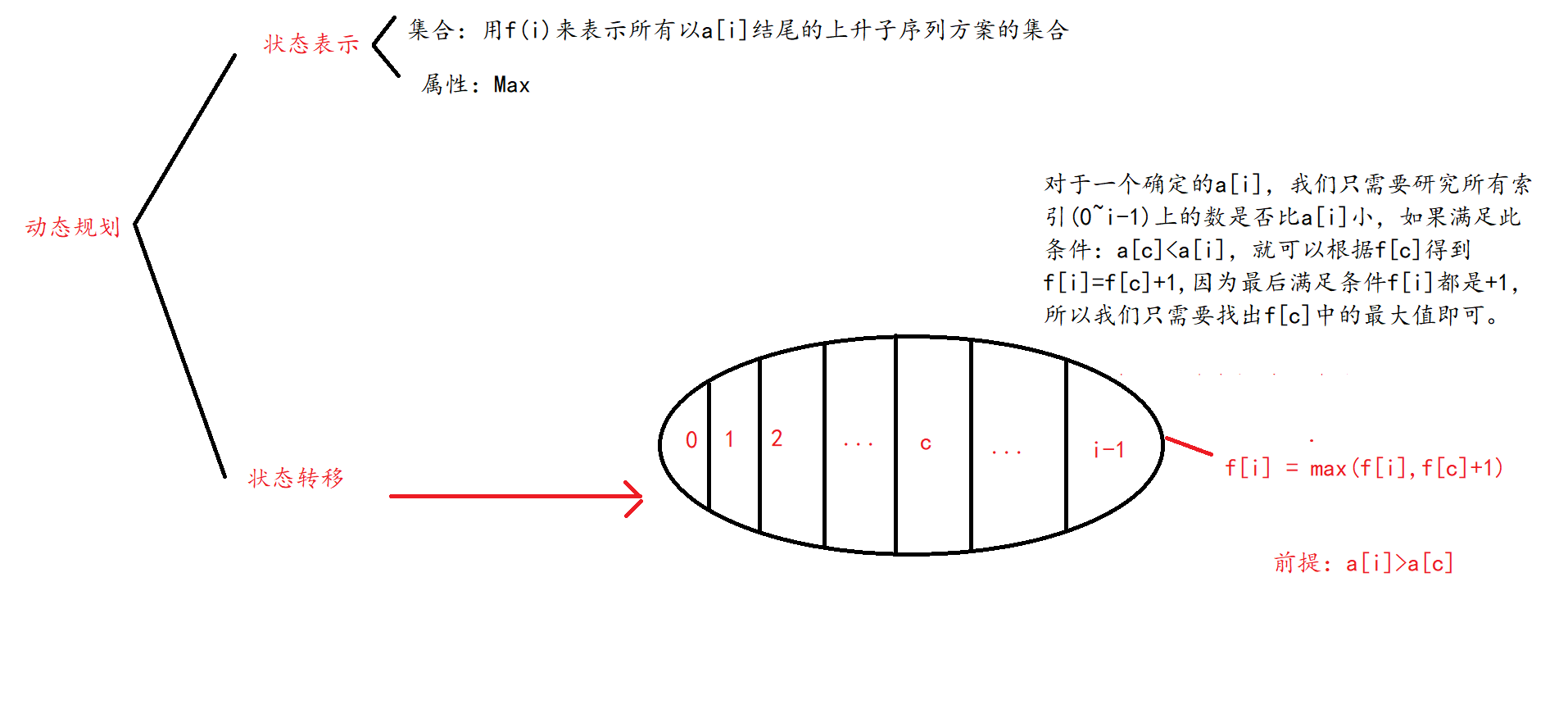
接下来这道题就是上面两道题的简单僵硬的拼接，会稍微复杂一些，但是原理一样

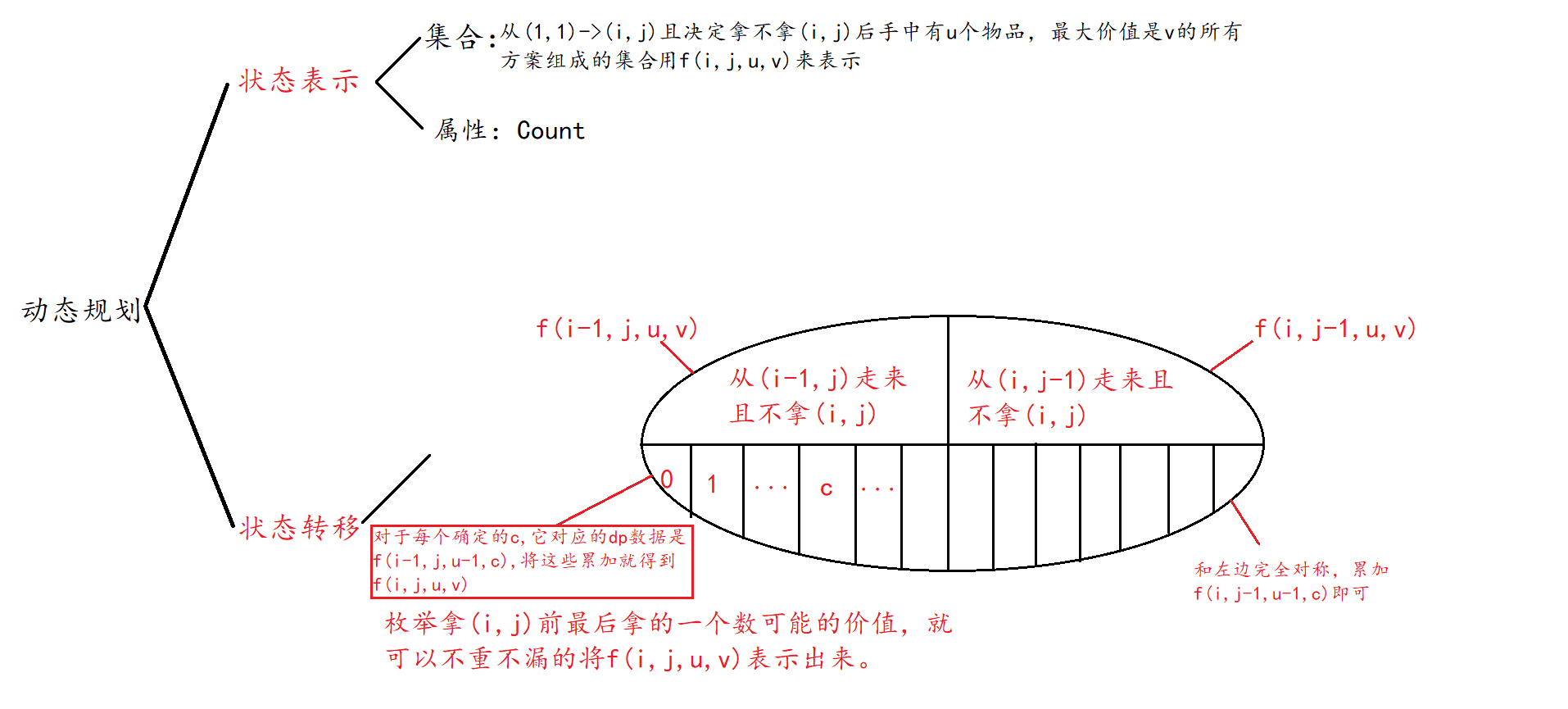
题目3、描述：X 国王有一个地宫宝库，是 n×m 个格子的矩阵，每个格子放一件宝贝，每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是 k 件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这 k 件宝贝。

输入格式

第一行 33 个整数，n,m,k，含义见题目描述。

接下来 n 行，每行有 m 个整数 Ci用来描述宝库矩阵每个格子的宝贝价值。

输出格式

输出一个整数，表示正好取 k 个宝贝的行动方案数。

该数字可能很大，输出它对 1000000007 取模的结果。

数据范围

1≤n,m≤50 1≤k≤12 0≤Ci≤12

输入样例1：

 2 2 2
 1 2
 2 1

输出样例1：

 2

输入样例2：

 2 3 2
 1 2 3
 2 1 5

输出样例2：

 14

分析图：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 const int N = 55;
 const int MOD = 1000000007;
 int a[N][N];//存原始输入数据
 int dp[N][N][13][14];
 int res;
 //前两维表示现在走到哪个坐标(i,j).
 //第三维表示从(1,1)->(i,j)并且决定了(i,j)位置上的宝贝选不选后手中的宝贝数，
 //最后一维表示从(1,1)->(i,j)并且决定(i,j)位置上的宝贝选不选后手中宝贝的最大值
 //所以，整个dp数组表示的就是：从(1,1)走到(i,j)，手中有n个物品，最大的那个是C的所有方案的集合。
 //属性：且存的值是所有方案的和。 
 int n,m,k;
 int main(){
     scanf("%d%d%d",&n,&m,&k); 
     for(int i=1;i<=n;i++){
         for(int j=1;j<=m;j++){
             scanf("%d",&a[i][j]);
             a[i][j]++;//因为宝贝价值可能为0，所以我们初始化dp是要用到-1这个数，会导致数组越界，所以我们人为将价值+1 
         }
     }
     
     //要先初始化一下dp
     dp[1][1][0][0] = 1;//表示从(1,1)->(1,1)且不拿
     dp[1][1][1][a[1][1]] = 1;// 表示从(1,1)->(1,1)且拿，
     //为什么等于1？因为你拿不拿我不关心，反正你是走到(1,1)这个点了，那就有一种方案。 
     
     //状态转移
     for(int i=1;i<=n;i++){
         for(int j=1;j<=m;j++){
             for(int u=0;u<=k;u++){
                 for(int v=0;v<=13;v++){
                     int& val = dp[i][j][u][v];//设置一个引用 方便修改
                     //不拿当前(i,j)宝贝 且从(i-1,j)走来 
                     val = (val + dp[i-1][j][u][v]) % MOD;//及时取模，防止爆int
                     //不拿当前(i,j)宝贝 且从(i,j-1)走来 
                     val = (val + dp[i][j-1][u][v]) % MOD;
                     //请注意下面两行注释： ！！！我们要忠实于我们对dp的定义！！！ 
                     
                     //拿当前(i,j)宝贝，但是我们要注意，拿完后我们手中的最大价值是v，所以当前(i,j)==v
                     //且拿完后我们手中的宝贝数会大于1. 
                     if(u>0&&a[i][j]==v){
                         for(int c=0;c<v;c++){
                         //则拿(i,j)前 拿的最后一个物品价值必然小于(i,j)的价值.
                         //则将所有这些方案加起来就可以不重不漏的表示dp[i][j][u][v].
                          
                             val = (val + dp[i][j-1][u-1][c]) % MOD;//从(i,j-1)走来且拿
                             val = (val + dp[i-1][j][u-1][c]) % MOD;//从(i-1,j)走来且拿    
                         }
                     }
                 }
             }
         }
     } 
     
     //所有状态运算完成后，我们想要的是从(1,1)->(n,m)且最后拿的宝贝件数是k的所有方案之和，而并不关心这些物品的价值是多少
     //所以：。。。将所有方案--[n][m][k][?]  累加起来即可
     for(int i=0;i<=13;i++)
         res = (res + dp[n][m][k][i]) % MOD;
      
     cout<<res<<endl;
     return 0;
 }