AtCoder Grand Contest 008题解
\(A\)
分类讨论就行了
然而我竟然有一种讨论不动的感觉
int x,y;
inline int min(R int x,R int y){return x<y?x:y;}
inline int min(R int a,R int b,R int c,R int d){
return min(min(a,b),min(c,d));
}
inline int calc(R int x,R int y){return y>=x?y-x:x-y+2;}
int main(){
scanf("%d%d",&x,&y);
printf("%d\n",min(calc(x,y),1+calc(-x,y),1+calc(x,-y),2+calc(-x,-y)));
return 0;
}
\(B\)
发现最优策略一定是选择一段长度为\(k\)的区间,这个区间之外的数可以任意选或不选,区间内的数必须全选或全不选,那么枚举区间即可
const int N=5e5+5;
int a[N],n,k;ll Pre[N],suf[N],sum[N],res;
int main(){
scanf("%d%d",&n,&k);
fp(i,1,n)scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];
fp(i,1,n)Pre[i]=Pre[i-1]+(a[i]>=0?a[i]:0);
fd(i,n,1)suf[i]=suf[i+1]+(a[i]>=0?a[i]:0);
for(R int l=1,r=k;r<=n;++l,++r)
cmax(res,Pre[l-1]+suf[r+1]+max(sum[r]-sum[l-1],0ll));
printf("%lld\n",res);
return 0;
}
\(C\)
首先\(T,S,Z\)型的完全不用考虑因为肯定不合法,\(O\)型的肯定是自己放自己的,\(I,J,L\)都是可以自己跟自己拼成一个合法的,以及有可能\(I,J,L\)共同拼成一个合法的,讨论一下就行了
ll I,O,T,J,L,S,Z,res;
int main(){
cin>>I>>O>>T>>J>>L>>S>>Z;
cmax(res,(I-(I&1))+O+(J-(J&1))+(L-(L&1)));
if(I&&J&&L)--I,--J,--L,cmax(res,(I-(I&1))+O+(J-(J&1))+(L-(L&1))+3),++I,++J,++L;
cout<<res<<endl;
return 0;
}
\(D\)
首先把所有数按\(x\)排序,那么按照这个顺序把\(x_ii\)前面的\(i-1\)个\(i\)给填满,以及记得剩下的\(n-i\)个数必须得填在\(x_i\)的后面
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=505;
int a[N*N],st[N*N],x[N],id[N],top,n;
inline bool cmp(const int &a,const int &b){return x[a]<x[b];}
inline void ins(R int x){fp(i,1,n-x)st[++top]=x;}
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d",&n);
fp(i,1,n)scanf("%d",&x[i]),a[x[i]]=i,id[i]=i;
sort(id+1,id+1+n,cmp);
R int i=1,j=1;
for(;i<=n;++i){
R int c=0;
while(c<id[i]-1){
while(j<x[id[i]]&&a[j])ins(a[j++]);
if(j==x[id[i]])return puts("No"),0;
a[j]=id[i],++c,++j;
}
}
while(233){
while(j<=n*n&&a[j])ins(a[j++]);
if(j>n*n)break;if(!top)return puts("No"),0;
a[j++]=st[top--];
}
puts("Yes");
fp(i,1,n*n)printf("%d ",a[i]);
return 0;
}
\(E\)
这题是真的神仙啊……完全想不到
以下可以看做是题解的翻译
首先我们从\(i\)向\(p_i\)连边,那么显然会形成若干个环
对于每个环我们单独考虑,在环里对于每个点向\(p_i\)或者\(p_{p_i}\)连边,那么总共有四种情况(借用题解里的图)
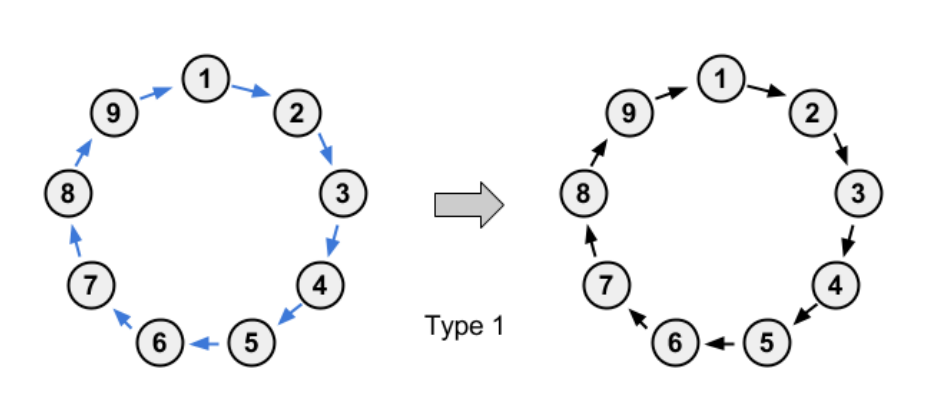



-
得到一个不变的图
-
得到一个同构的图,此时环的大小为奇数(且大于\(1\))
-
得到两个完全相同的环,此时环的大小为偶数
-
得到一个环,环上伸展出去若干触手,且每个点只伸展出一个触手,触手无分叉
那么对于输入,我们把\(i\)向\(a_i\)连边,首先此时得到的图要合法(即由环和长触手的环构成),然后考虑它能反过来构成多少原来的环
对于大小为\(k\)的环,假设有\(c_k\)个,那么每一个都可以通过方法一变回环,如果环的大小大于\(1\)且是奇数那么还可以通过方法二,也可以把两个环给拼在一起(注意拼在一起的方案数为\(k\))。设\(f_{i}\)表示\(i\)个环变回去的方案数,最终\(f_{c_k}\)就是答案了,这个可以\(O(c_k)\)的\(dp\)出来
然后来考虑触手,把触手接回环里有两种方案
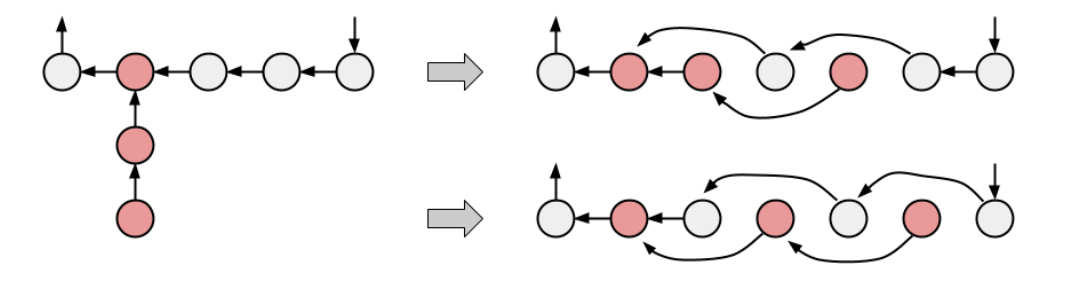
那么设\(l_1\)表示这个触手的长,\(l_2\)表示这个触手距离上一个触手的距离,则这个触手缩回去的方案,当\(l_1<l_2\)时为\(2\),\(l_1=l_2\)时为\(1\),\(l_1>l_2\)时为\(0\)
综上,时间复杂度为\(O(n)\)
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int P=1e9+7;
inline void upd(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int add(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))(y&1)?res=mul(res,x):0;
return res;
}
const int N=1e5+5;
int to[N],deg[N],cir[N],cnt[N],dp[N],col[N],len[N];
int n,res,tim;
inline int calc(R int x,R int y){return (x<y)+(x<=y);}
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d",&n),res=1;
fp(i,1,n)scanf("%d",&to[i]),++deg[to[i]];
fp(i,1,n)if(!col[i]){
R int u=i;
for(++tim;!col[u];u=to[u])col[u]=tim;
if(col[u]==tim)for(;!cir[u];u=to[u])cir[u]=1;
}
fp(i,1,n)if(deg[i]>cir[i]+1)return puts("0"),0;
fp(i,1,n)if(!deg[i])
for(R int u=i,l=0;!cir[u];len[to[u]]=++l,u=to[u]);
fp(i,1,n)if(cir[i]){
R int u=i,fir=0,firlen=0,k=0,las=0;
for(;cir[u];cir[u]=0,u=to[u])
if(++k,len[u]){
if(!fir){fir=las=k,firlen=len[u];continue;}
res=mul(res,calc(len[u],k-las)),las=k;
}
fir?res=mul(res,calc(firlen,fir+k-las)):++cnt[k];
}
fp(i,1,n)if(cnt[i]){
R int op=(i&1)+(i>1);
dp[0]=1;
fp(j,1,cnt[i]){
dp[j]=mul(dp[j-1],op);
if(j>1)upd(dp[j],1ll*i*(j-1)%P*dp[j-2]%P);
}
res=mul(res,dp[cnt[i]]);
}
printf("%d\n",res);
return 0;
}
\(F\)
更神仙的一道题
这题似乎有两种理解方法,这里只讲其中一种(另外一种枚举中点的我实在是看不懂啊……)
首先,我们设\(f(u,d)\)表示所有离\(u\)的距离不超过\(d\)的点构成的点集,如果直接去数有多少合法的\(d\),显然会使很多点集被重复计数
考虑如何才能不重不漏的数完。首先整棵树肯定是合法的,那么我们规定染色的时候不能染完整棵树,最后答案\(+1\)即可
先假设所有的点都是特殊点,那么\(f(i,d_1)\)和\(f(j,d_2)\)如果相等,设这条路径为\(i,p_1,p_2,...,p_v,j\),那么必定存在点\(p_k\)满足\(f(i,d_1)=f(p_1,d_1-1)=f(p_2,d_1-2)=...=f(p_{k-1},d_3+1)=f(p_k,d_3)=f(p_{k+1},d_3+1)=...=f(p_v,d_2-1)=f(j,d_2)\)
那么我们对于这个点集只要数\(f(p_k,d_3)即可\),最终可以把条件转化为\(f(i,d)\)合法当且仅当对于任意一个和\(i\)相邻的点\(v\),\(f(v,d-1)\neq f(i,d)\)
综上,条件为
\(1.f(i,d)\)不为全集
\(2.\)对于任意一个和\(i\)相邻的点\(v\),\(f(v,d-1)\neq f(i,d)\)
第一个条件,我们只要求出\(i\)到树上任意一点的最远距离\(dis_i\),那么\(d\leq dis_i-1\)
第二个条件,易知\(f(v,d-1)=f(i,d)\)等价于以\(i\)为根时,除了\(v\)这棵子树内,其它所有点均被染色,那么记下从\(i\)出发不经过\(v\)的最长路径\(len(i,v)\),则有\(d-1\leq len(i,v)+1-1\),即\(d\leq len(i,v)+1\)
然后现在有的点可能不是特殊点……事情变得辣手了起来……
先给出结论,一个\(d\)满足上界的\(f(i,d)\)合法,要么\(i\)是特殊点,要么以\(i\)为根时,这种染色方案能把某棵内部存在特殊点的子树内所有点全部染完
前一种情况很容易,因为如果\(i\)是特殊点显然\(d\)的下界为\(0\)
对于后一种情况,假设对应的特殊点为\(u\),显然\(f(i,d)\)应该是以\(i\)为中点的一个点集,而我们需要从\(u\)拓展过来,所以这个点集的中点必定是偏向\(u\)的,所以只有当这个点集染完了\(u\)所在的子树且向\(i\)的其它子树扩展了足够的距离之后,才能满足\(f(i,d)\)是一个合法的点集,即\(i\)能够作为这个点集的中点,此时\(d\)的下界为以\(i\)为根时,满足\(v\)的子树中存在特殊点,且\(v\)的子树内离\(v\)距离最大的点距离最小,的距离
于是我们可以通过两遍树形\(dp\)求出答案,时间复杂度为\(O(n)\),具体细节可以参考代码
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
typedef long long ll;
const int N=2e5+5,inf=0x3f3f3f3f;
struct eg{int v,nx;}e[N<<1];int head[N],tot;
inline void add(R int u,R int v){e[++tot]={v,head[u]},head[u]=tot;}
inline int max(R int x,R int y){return x>y?x:y;}
inline int min(R int x,R int y){return x<y?x:y;}
int d1[N],d2[N],d3[N],d4[N],sz[N],fa[N];
//d1子树内离u最远的距离
//d2来自父亲的离u最远的距离
//d3存在特殊点的子树的最小的距离
//d4父亲不经过u这棵子树时能到达的最远距离
ll res;char s[N];int n;
void dfs1(int u){
sz[u]=(s[u]=='1'),d3[u]=sz[u]?0:inf;
go(u)if(v!=fa[u]){
fa[v]=u,dfs1(v),sz[u]+=sz[v],cmax(d1[u],d1[v]+1);
if(sz[v])cmin(d3[u],d1[v]+1);
}
}
void dfs2(int u){
if(fa[u])d4[u]=d2[u]-1;
R int se=0,fi=0,to=0;
go(u)if(v!=fa[u]){
if(d1[v]+1>=fi)to=v,se=fi,fi=d1[v]+1;
else cmax(se,d1[v]+1);
}
go(u)if(v!=fa[u]){
d2[v]=max(v==to?se:fi,d2[u])+1;
dfs2(v);
}
}
int main(){
scanf("%d",&n);
for(R int i=1,u,v;i<n;++i)scanf("%d%d",&u,&v),add(u,v),add(v,u);
scanf("%s",s+1);
dfs1(1),dfs2(1);
fp(u,1,n){
R int mn=min(d3[u],sz[u]==sz[1]?1e9:d2[u]);
R int mx=max(d1[u],d2[u])-1;
go(u)cmin(mx,(v==fa[u]?d1[u]:d4[v])+1);
res+=max(mx-mn+1,0);
}
printf("%lld\n",res+1);
return 0;
}


