对极几何-本质矩阵-基本矩阵

对极几何-本质矩阵-基本矩阵

转自知乎文章：https://zhuanlan.zhihu.com/p/33458436

记得之前的相机矩阵，这是针对单个相机的，可我们知道单个相机图片并不能告诉我们物体的深度信息，这时至少需要两个相机，这样在两视图间内在的射影几何关系就是对极几何，而基本矩阵就算对极几何的代数表示。

对极几何

如果仅看一个相机，我们并不能知道深度信息，可如果有两个相机的话（就像人有两只眼睛）我们就能得到深度的信息，

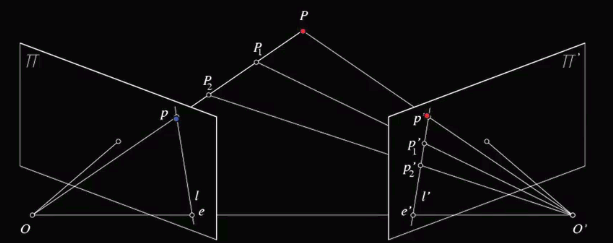
上图O和O'是两个相机中心，P点是物体所在，如果我们只看左边图像 $\pi$ 上的点p，我们不能知道物体到底是在哪，点P1、P2或其他地方，可有了右边图像 $\pi'$ 上的p'我们就能得到物体点P

在上图，我们把两相机中心的连线OO'成为基线，把他们与观测物体的平面OO'P成为对极平面，对极平面与两相机图像的交线l和l'称为对极线，而OO'与两图像的交点e,e'就是对极点。

随着观测点P的上下移动，对极平面也会围绕基线旋转

我们可以看到在左图对极平面旋转时对极点是不变的，而在相机图像上所有对极线都会交于对极点，这个对极点就是另一个相机中心在其图像上的像，当然正如右图所示，对极点可以在图像外。

本质矩阵（Essential matrix）

几何表示是便于理解的，可是计算机并不懂，我们要将其转为代数形式。

我们知道由相机1到相机2是刚体运动，那么观测点P在相机1坐标系的坐标就可以通过刚体转换变成相机2坐标系下，

$P'=RP+T\\$

其中R和T分别表示旋转和平移，如果我们将其左叉乘一个T，即 $T\times P'=T\times RP+T\times T=T\times RP\\$

其中 $T\times P'$ 表示对极平面的法线，若再左点乘一个P'得到

$P'(T\times P')=P'(T\times RP)\\$

由于P'与法线TxP'是垂直的，所以有

$0=P'(T\times RP)\\$

我们知道两向量的叉乘可以转换为一向量的反对称矩阵与另一向量的点乘，于是 $P'(T\times RP)=P'[T_\times]RP=0\\$

$[T_\times]$ 表示T的反对称矩阵，我们让 $E=[T_\times]R$ ,那么

$P'^TEP=0\\$

这个E就是本质矩阵.

基本矩阵

还记得我们将世界坐标系的观测点转换到2D图像点的方法吗，没错，就是用相机矩阵，而相机矩阵又分为内参和外参的，代数表示为 $P_{im}=K_{int}\Phi_{ext}P_w\\$

K和 $\Phi$ 分别表示内参矩阵和外参矩阵，P_im和P_w分别表示图像点和世界点，如果我们把经外参矩阵转换到相机坐标系的世界点称作P_c，那么上式可化为 $P_{im}=K_{int}P_c\\$

现在我们考虑左右两视图，又由于K是可逆的，有 $P_{c,left}=K^{-1}_{int,left}P_{im,left}\\P_{c,right}=K^{-1}_{int,right}P_{im,right}$

还记得上面的本质矩阵吗

$P_{c,left}^TEP_{c,right}=0\\$

将矩阵相乘

$(K^{-1}_{int,left}P_{im,left})^TE(K^{-1}_{int,right}P_{im,right})=0\\ P_{im,left}^T((K^{-1}_{int,left})^TEK^{-1}_{int,right})P_{im,right}=0$

我们另 $F=((K^{-1}_{int,left})^TEK^{-1}_{int,right})$ ,上式化简为 $P_{im,left}^TFP_{im,right}=0\\$

而F就是我们的基本矩阵

结尾

关于基本矩阵的性质和计算，希望大家能自己去了解，我就在此打住了

参考资料

《计算机视觉中的多视图几何》—Richard等
intro to computer vision——Udacity

相关网址：

Monocular slam 的理论基础(1)：https://blog.csdn.net/heyijia0327/article/details/50758944

Monocular slam 的理论基础(2)：https://blog.csdn.net/heyijia0327/article/details/50774104

posted on 2018-08-12 10:34 melodybinbin 阅读(7997) 评论(0) 编辑收藏举报

刷新页面返回顶部