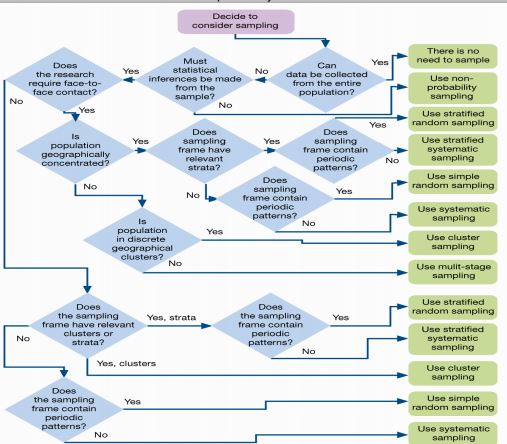
抽样调查
有限群推断
计算人口特征(人口普查)
估计人口特征(抽样调查)
普查与抽样调查
预算和时间
范围
精确性
可行性
================================
抽样调查的步骤
人口是多少?
感兴趣的参数是什么?
抽样框架是什么?
是否需要样本量?
要多少钱?
*实际绘制样品的元素的列表
=============================
基本抽样计划
简单随机采样(SRS)
分层抽样,分层抽样法,分层取样
系统抽样
分群[组]抽象法
多级采样
=============================
简单随机采样的基本概念
从人群中随机选择一个人口单元,直到达到一组样本量“n”
在每个选择过程中,其余的人口单位被选中的机会均等。
一组样本以相同的概率发生。
=============================
种群特性
种群总数: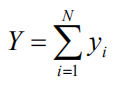
总平均,全平均: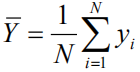
总体比例: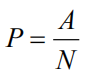
比,比率:
=====================================
SRS下的总体特征及估计
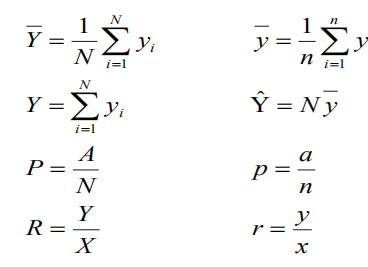
===========================================
取样质量
精确(性),准确(性)-系统差异
由于某些已知的或未知的影响而造成的测量的变化,这些影响“导致”分数(结果)比另一个方向更倾向于一个方向。
精确度,准确(性)-抽样误差
给定样本与潜在种群的不同程度。
在小样本的情况下,采样误差往往很大,并且随着样本量的增加而减小。
=======================================
SRS下估计器的性能(略)
=======================================
性质
估计器的基本性质
样本比例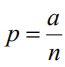 是一个无偏估计量
是一个无偏估计量
人口比例 的方差是
的方差是 ,其中
,其中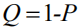
======================================
抽样误差与样本量
从无限人口中取n个样本估计比例p时的采样误差e
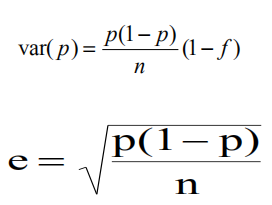
======================================
置信区间
在1000家企业的样品中,280家企业(28%)受到了掠夺机构的骚扰。
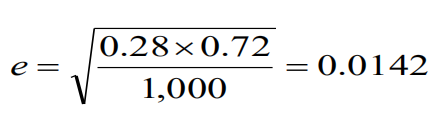
采样误差为1.42%。
==========================================
置信区间
在1,000家企业中,有280家(28%)受到掠夺性机构的骚扰。
采样误差为1.42%。

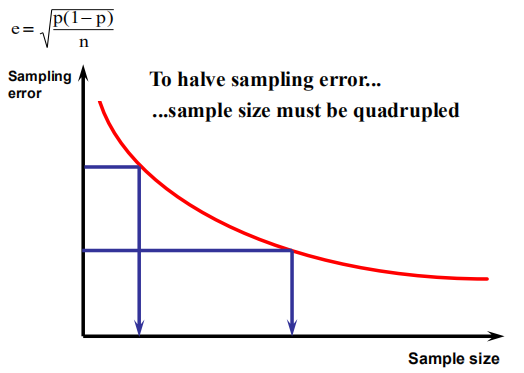
为了使采样误差减半……...sample大小必须翻两番
当从大小N的群体获取的大小为n的样本估计比例P时,采样误差E
 有限群校正
有限群校正
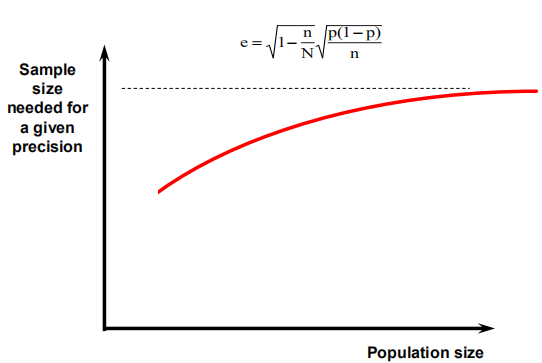
给定精度所需的样本量。
====================================================
分层抽样,分层抽样法,分层取样
根据分层样本设计,使用GillNet对短鼻鱼进行采样设计
====================================================
分层抽样的优点
1.确保每个阶层(亚群体)都有很好的权重。
2.如果抽样分配得当,可能会导致标准误差较小的估计。
3.小地层将不会丢失
分层抽样的缺点
1.比SRS更复杂
2.需要提前确定地层。因此,取样前所需的信息比SRS所需的信息要多。
======================================================
系统抽样
一种概率抽样,其中选择了人口中的Kth成员。
 =========================================================
=========================================================
系统抽样程序说明
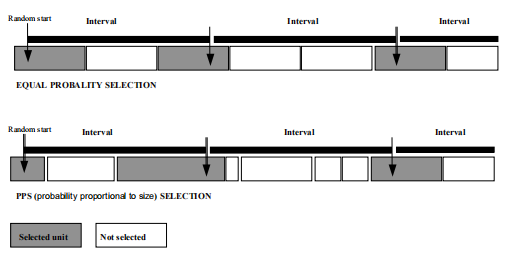
=====================================
有利条件:
简单。它允许研究者将系统或过程的程度添加到受试者的随机选择中。
保证将对人群进行均匀采样。存在允许对受试者进行聚类选择的简单随机采样的机会。这在系统抽样中被系统地消除了。
不利:
-选择过程可以与群体内的隐藏的周期性特征相互作用。如果采样技术与特征的周期性相一致,则采样技术将不再是随机的,样本的代表性也会受到损害。
======================================
分群抽样
采样单元包含多个人口元素。
对于简单的聚类抽样,每个聚类包含相同数量的元素;随机选择簇;所有选定元素都包含在样品中
================================
假设人口中有A个集群,则选择a个集群。
每个集群包含B个元素。
因此,样本大小为:n=aB。
种群大小为N=AB
=============================
样品平均值也是a簇的平均值
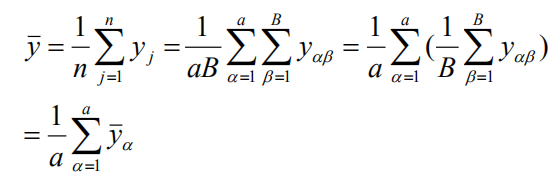
就估计量的方差而言,情况与SRS完全相同。
性质:样本方差的无偏估计是:
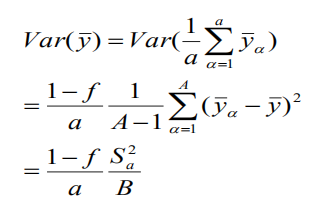
==============================================
关键:
这种简单的群集采样案例非常类似于元素的SRS。
估计量的精度仅取决于聚类方差之间的大小。因此,当选择集群时,我们要在方差之间进行“最小限度”,或者等价地,在方差内的“最大限度”。
不幸的是,在许多情况下,集群是自然形成的。例如,县、班等。
=================================================
多级采样
第1阶段
随机采样簇(或应用其他采样方法)
第2阶段
-从所选群体中随机抽取个人样本