排序
PCA主元件分析，主成分分析
FA因子分析
CA对应分析
===========================================
主元件分析，主成分分析
主成分分析(PCA)是一种用于数据的压缩和分类的技术。其目的是通过查找新的变量集(样本)来降低数据集(样本)的维数，这些变量集比原始变量集小，但保留了大多数样本的信息。
我们所说的信息是指由原始变量之间的相关性给出的样本中的变化。新的变量，称为主成分(PC)，是不相关的，并按每个信息保留的总信息的比例排序。
原始数据：
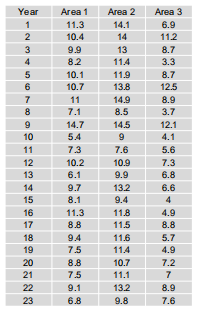
给定n维空间中的m点，对于大n，如何将m点投影到1维空间上？
选择一条适合于数据的线，这样点就会沿着这条线很好地分布。
正式地，最小化与线路的距离平方和
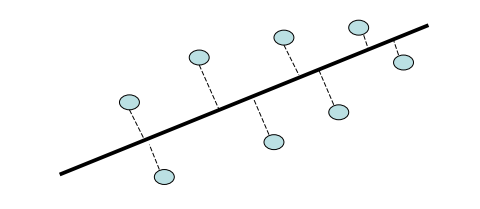
为什么是平方和？因为它允许快速最小化
对于一个数据点和一条通过点(0，0)的直线，最小化距离到这条线的平方和等于最大化这条线上投影的平方和。
=============================================
PCA：一般方法
从K个原始变量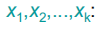
产生k个新变量
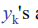是主成分
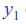尽可能多地解释数据集的原始差异
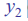尽可能多地解释剩余的差异
===============================================
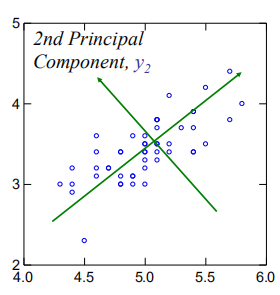
图释:
第一主成分，Y1
第二主成分Y2
====================================
特征值：
第一主成分就是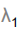
，就是第一特征值
第二主成分就是
，就是第二特征值
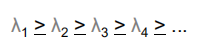
如果矩阵是标准化的，则平均λj=1。
是协方差矩阵的第一特征向量和第一主成分系数
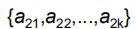是协方差矩阵的第二特征向量，是第二主成分的系数。
第k个协方差矩阵的特征向量和第k个主要成分的系数
======================================
PCA术语
第j主成分是所有变量的线性组合
系数，ajk，是特征向量的元素，并将原始变量（X）（标准化，如果使用相关矩阵）与分量（y）相关联。
分数是分量（x）上单位的值(使用系数产生)，即系数值与相对应的X变量相乘之后的值。第j个主要部件第i个单位的数值。
按分量计算的方差数按特征值、λ表示。
按分量计算的方差比例由λj/Σλ给出。
因为变量与分量的系数相关性，产生了主成分上K原始变量的加载。
=====================================
原始数据：
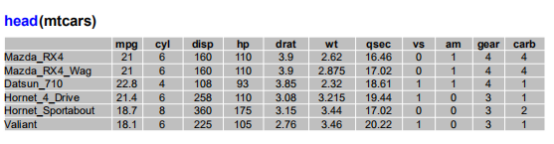
PCA处理后每个主成分的系数值
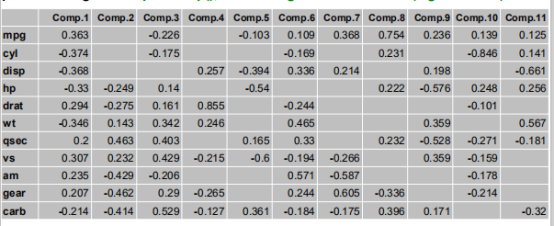
PCA处理后每个主成分的score值：
===========================================
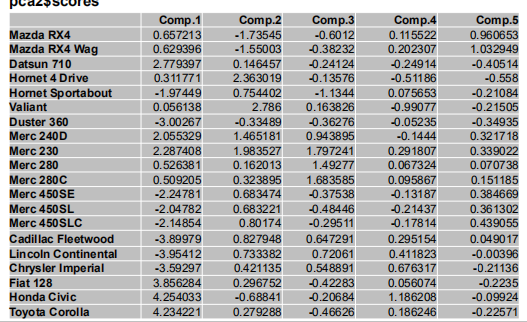
PCA：潜在问题
可以变量间缺乏独立性，因为没有问题
可以缺乏正态，因为正态是可取的，但不是必要的
在任何两个变量之间不单调，应对是使用对应分析，即
数据矩阵中的多个零点，应对是使用对应分析。
==============================================
注意：
主要成分取决于用于测量原始变量的单位以及它们所承担的值的范围。
我们通常在使用PCA之前对数据进行标准化。
=============================================
因子分析FA是一种数据降维工具。--（因子分析就是数据降维）
从一组相关变量中删除冗余或重复，把相关的变量放在一个因子中，实在不相关的因子有可能被删掉。用一组较小的“派生”变量表示相关变量，这个派生就是新的因子。形成彼此相对独立的因素，就是说新的因子彼此之间正交。
两种类型的“变量”：
1.潜在变量，即因素，就是降维后的因素。
2.观测变量，就是拿到的真实变量。
===========================================
因子分析的一些应用分析--（应用：筛选变量）
1.确定基本因素：
A.聚类变量为齐次集
B.创建新变量，就是创造出了因子
C.使我们能够洞察类别
2.变量筛选
A.标识分组，使我们能够选择一个变量来表示多个变量，就是一个因子来表示多个变量。
B.在回归中有用(回忆共线性)，在多元回归中我们删去有共线性的X变量。
3.总结：允许我们使用几个因素来描述许多变量。
4.物体的聚类：帮助我们根据他们的因素分数将对象（人员）放入类别中
===================
数据矩阵----（1.构建数据矩阵，该数据矩阵是相关矩阵，PCA之后变为因子矩阵）
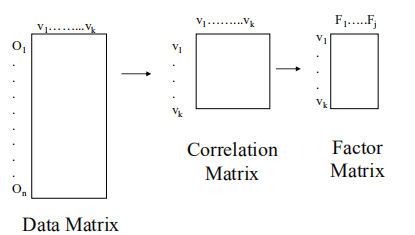
因子分析完全依赖于变量之间的相关性，建立相关矩阵之后
因子分析总结了相关结构。
===================================
选择因素数
直观看，是将X的分量线性相关组成因子后，不相关因子的的数量。
只有当因素数小于X的变量数时才有用(回忆“数据约简”)。即要求因子矩阵为瘦长型表格。
使用“主成分”来帮助决定
因素的数量等于变量的数量
每个因素都是输入变量的加权组合，即score总和：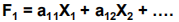
============================
特征值：
若要选择要使用的因素，请从主成分分析中考虑特征值。
两种解释：
系数等于变量数的特征值
特征值等于方差在数据中的描述因子。
须遵守的规则：
因子数>1
碎石图判断，断崖前一个比后一个表示的强太多。
解释方差比例，选择解释方差最多的前几个。
找好解释的因子
注：特征值之和等于项目数，即特征值数等于系数个数。
===================================
因子分析中的步骤
因素分析通常分四个步骤进行。
- 计算所有变量的相关矩阵，而PCA用的是特征矩阵
- 要素提取，仅在此处需要使用PCA
- 要素轮换
- 就基本因素的数量作出最后决定
==================================
相关矩阵
为所有变量生成相关矩阵
确定与其他变量无关的变量
如果变量之间的相关性较小，它们不太可能共享共同因素（变量必须相互关联，才能使因子模型合适)。
绝对值大于0.3的相关系数表示可接受的相关性，即相关系数大于0.3则把它们放在一堆。
从视觉上检查因素模型的适当性。
======================================
因素抽出
这一阶段的主要目标是确定各种因素。
在这里，可以对一组测量变量背后的因素进初始决策。
利用主成分分析得到初始因子的估计。
PCA是最常用的提取方法。其他因素提取方法包括：
最大似然方法，最大似然量法，极大似然法
主轴因素
α法
广义最小二乘法
图像分解
===========================================
因素抽出
在主成分分析中，形成观测变量的线性组合。
第一个主成分是样本中方差最大的组合(第一个提取因子)。
第二主成分占第二大方差，与第一(第二提取因子)无关。
连续分量解释总样本方差的逐渐变小的部分，并且所有的分量彼此不相关。
为了决定我们需要多少个因素来表示数据，我们使用了两个统计标准：
特征值，以及scree plot:
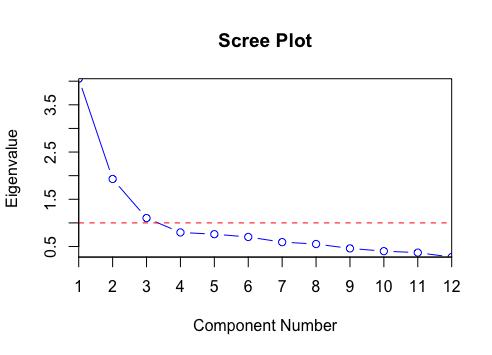
在确定因子数时，通常只考虑特征值大于1的因素。
方差小于1的因素并不比单个变量好，因为每个变量的方差预计为1。
对Scree图的检查提供了与每个因素相关联的总方差的可视化。
陡坡显示出很大的因素。
逐渐消失（SCREE）显示的其他因素通常低于1的特征值。
在选择因素的数量时，除了统计标准外，还应根据概念和理论依据作出初步决定。
在现阶段，关于因素数量的决定不是最终的。
======================================================
因素轴转为了让因子之间差距尽量大
在这个步骤中，因子被旋转。
非旋转因素通常不是很容易解释的(比如因素1与所有变量都相关，因素二与前四个变量相关)
对因素进行旋转，使它们更有意义，更易于解释(每个变量都与最小数量的因素相关联)。
不同的旋转方法可能导致识别出一些不同的因素。
四分位差：
简化行-变量负载在一个因素上高，在其他因素上低。
最大方差法：
简化列
更清楚地分离因素
每个因素都有变量，要么加载高，要么加载非常低。
均等法：
两者之间的妥协-很少使用
最流行的旋转方法是Varimax旋转。
Varimax使用正交旋转产生不相关因素/成分
Varimax试图最小化一个因子负载较高的变量的数量。这增强了因素的可解释性。
==================================================
最后决定
关于要选择的因素数量是最可解释的旋转溶液的因素数量。
若要标识因素，选择同一因素的大量负载的组变量。
加载图为可变集群提供了可视化。
根据变量的含义解释因素
这项决定应以下列各项为指导：
关于过去研究或理论中因素数量的先验概念信念
第二步计算出来的特征值
在步骤3中计算的旋转解的相对可解释性。
===============================================
前提：
各因子和线性相关。？？？
对于每一对变量，数据应该有一个二元正态分布。？？？
观察是独立的。
因子分析模型假定变量由共同因素和独特因素决定。所有独特因素都被假定为互不相关。
=================================================
因子分析(FA)与PCA比较
PCA分析方差，FA分析协方差。
PCA是用最少的因素提取出尽可能多的方差。
FA是为了解释尽可能多的关联与最小数量的因素。
PCA给出了一个独特的解决方案。如果保留所有主成分，则解释所有差异。就是结果可能是：
FA1：变量A，变量B，变量C，变量D和变量E
FA2：变量A，变量B，变量C和变量D
FA3：变量A，变量B，变量C和变量E
FA可以根据方法和公共估计给出多个解。
就是说有两机会改变最后的结果，第一次是抽取变量，第二次是轮转。
最好的理想结果是一种变量仅归因于一种因子。即结果是：
PCA1：变量A，变量D和变量C
PCA2：变量B和变量E
PCA与FA的区别在于FA还要旋转以及最开始时，PCA的矩阵是特征矩阵，而FA是相关矩阵。
===========================================
因子分析与聚类分析比较
都是数据约简技术..
因子分析是将原始变量集简化为较小的一组因素。
聚类分析是从观察或记录中形成组，从而将元素的原始数量减少到较少的组
因素分析可以看作是一种聚类技术，而不是集中在数据帧的列上，而不是行。
======================================
对应分析CA
也称倒数平均
站点分数的加权平均值对物种分值的影响，物种分值的加权平均对站点分数的影响。
同时排序矩阵的行和列
用于研究物种组合与立地特征的关系
站点通常跨越环境梯度，如果条件相互组合的话，有可能引起跨越环境梯度。
====================================================
对卡方矩阵进行CA
特征值
解释比例
比例累计函数
CA进行特征值分解，在较少的轴(主成分)中总结这种可变性。
对位置贡献最大的物种和地点的CA1评分最高。
分数以中心和比例为中心，可直接比较。
=================================
输出：
行和列和，总数X平方
可以在同一空间绘制的物种和样本分数。解释与NMDS中的样本分数和物种加权平均数相似。
-#axes=n-1表示数据矩阵的任何维数较低(样本或物种)。
特征值-每个轴的相对重要性，解释为总惯性的百分比解释。
==========================================
物种之间的距离是它们的卡方距离的二维近似。样本之间的距离也是卡方距离的二维近似。
物种与地点之间的距离不能被解释。
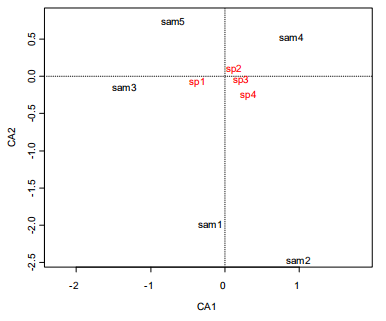
CA是如何工作的？
地点-物种矩阵
特征分析
类似于PCA，但在一些细节上有所不同
轴在物种和样本空间中旋转，目的是最大限度地保持它们的对应性。
互相平均
将物种得分计算为它们发生的地点的加权平均数。
用物种得分的加权平均法计算新的立地得分。
CA输出
产生主轴和分数
行(站点)和列(物种)的得分
第1轴具有最大的特征值（且占方差最大）.；最大化行和列之间的关联
后继轴考虑了残余变化，并具有较小的特征值。
在CA中很少使用超过2-3轴。
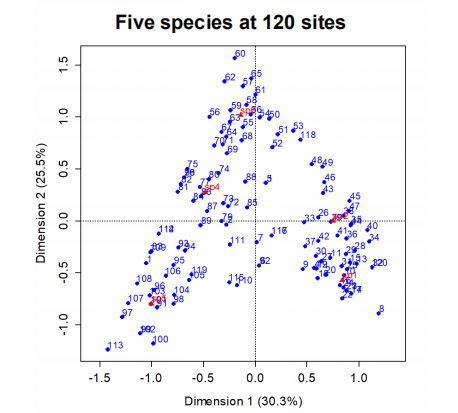
对应分析
第一轴总是信息最丰富的
所产生的轴数是由数据的维数决定的，而不是用户选项。
不是基于距离的，数据转换通常更重要。
直接对样品和物种进行排序
================================================
CA与PCA比较
这两种方法都是特征向量法。
PCA使用欧氏距离，CA使用Chisquare距离。
基本假设-PCA物种丰度分布为高斯分布(CA正态分布和单峰分布)。
CA正确排序第一轴上的点。
主成分分析中梯度末端的曲率和“缩进”导致对点的正确排序失败。马蹄铁效应
=================================================
CA优势
PCA的弱点：
假设物种之间和/或梯度是线性相关的。
样品在物种空间中进行排序。
“马蹄效应”中排序轴末端扭曲的结果
对应分析考虑了非线性单峰关系：
样本和物种的处理方式都是相似的，轴并不明确地表示物种空间。
代表环境梯度：一组由11种物种组成的综合数据集，它们对环境梯度具有无噪音的驼峰状反应。梯度在11个点(样本单位)取样，编号1-11。
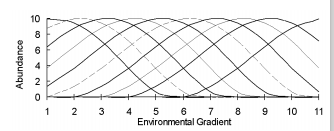
图19.1所示数据集的PCA和CA的比较。PCA曲线的梯度末端，而CA没有。向量表示环境梯度与轴向分数的相关性，即CA的环境梯度与轴向分数相关性更好。
===========================
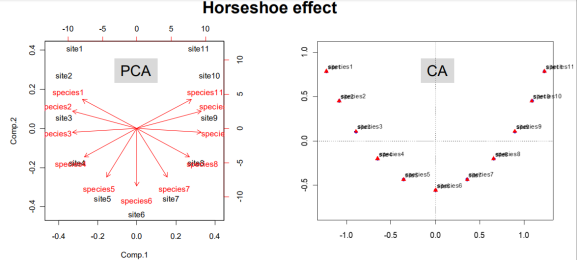
CA问题
第一CA轴是可靠的，但是第二轴和以后的轴是第一次产生“拱效应”的二次畸变。
向轴末端压缩的距离，中间延伸的距离
卡方距离赋予低丰度物种很高的权重，它夸大了含有几种稀有物种的样品的独特性。
======================================
降趋对应分析DCA
CA的“拱效应”是不想要的；CA中轴的末端也被压缩。
去趋势(去趋势对应分析，DCA)通过：
第一轴的5段平滑。分成几段(重量为1，2，3，2，1)，中心各为0。
将轴线重新标度为物种周转的“标准差”单位
只有前四个轴被调整，其余的被丢弃。
假设前提：
与CA相同
DCA并不是真正的分析。这是对CA的事后修改。
============================
主要坐标分析(PCoA)
与pca一样，pcoa是距离或不同矩阵的特征分析。
Eg：各种物种的分布呈片状分布，这使得相关函数、协方差函数和卡方函数不太适合定义关联。
r提供了一个计算距离的函数，dist()函数，它提供了相当窄的距离范围(欧几里得、曼哈顿、二进制、堪培拉和最大值)。
然而，vegdist {vegan}库提供vegdist()函数，LabDSV库提供dsvdis()函数作为替代，提供更多的索引，包括那些在植被生态学中常用的
在各种程序和库中使用的距离、不同或索引函数
非标准化：
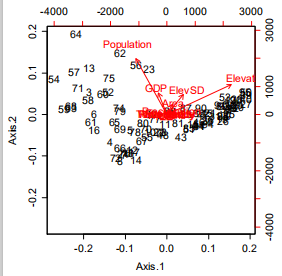
标准化后：
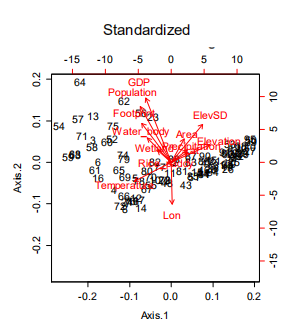
使用不同距离：
===========================================
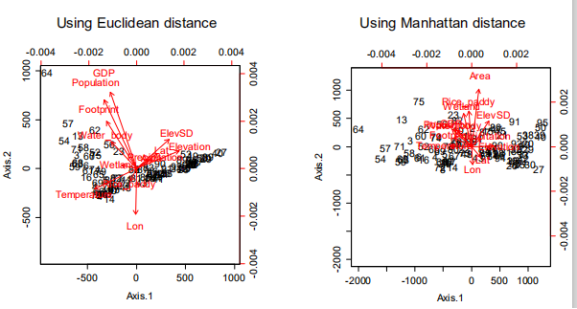
非度量多维标度(NMDS)
与度量MDS相比，非度量MDS基于样本对之间的排序相似性/差异性。
NMDS也可以使用任何关联度量，比如PCoA。
它更好地保持高维结构的几个轴。
它的缺点是它不是基于特征值解，而是基于数值优化方法，对于较大的数据集，计算往往会变得费时。就是将数值大小转化为数值排序。
=========================================
Bray-Curtis相似性(NMDS默认值)
它对单位的变化不变。
它不受两个群落中不存在的物种的增加/移除的影响。
它不受新群体的影响。
当相对丰度相同时，可以识别出总丰度的差异。
NMDS算法
1.选择关联度量，计算距离矩阵D
2.指定m，轴数
4.构造一个起始配置E。这可以用PCoA来完成。
5.将配置退到D上：
6.通过拟合Shepard图中的一条非参数(单调)回归曲线来度量m维构型与实际距离之间的关系。单调回归被限制为增长。如果使用参数回归线，则得到PCoA。
7.与拟合曲线的差异称为应力。
8.利用非线性优化程序，得到E的一个新估计，并进入第4步，直到收敛。
拟合优度和应力
应力测量（标准残差平方和）是原始距离和导出距离的函数，用于估计mds解决方案的拟合优度。
应力函数越小，导出的距离就越近。
=========================================
应力和维度的数量
应力值随维度的增加而减小
维度数可以通过屏幕应力图与维度数来计算，就像对于FA、PCA或聚类分析。
其中最佳数量对应于：
维度的首选数通常是2或3个，这样可以进行图形检查。
搜索通常从一个维度到五个维度。
度量和非度量迭代算法中最优数的识别
1.加一步评估应力函数
2.当添加进一步的维数并没有将应力值降低到可感知的程度时，该算法就停止了。
在两个维度上，通常认为低于0.05的应力值是令人满意的，
==============================================
冗余分析RA
检查一组变量（X）中有多少变化解释了另一组变量（Y）中的变化。
总结了“冗余”的响应变量(Y)与(即“解释”)一组解释变量(X)之间的线性关系。
基于与主要成分分析相似的原理并因此对数据做出类似的假设。
当X和Y变量之间的预期关系是线性的时是适当的
如果X和Y变量之间的期望关系是高斯的(例如气候和物种丰度)那么典型对应分析就更合适了。
==================================
找出Y的那些分量，它们是X的线性组合，并且（其中）代表尽可能多的Y方差。
假设：Y中的响应变量与X的解释变量有线性相关性。
冗余分析的思想是应用线性回归，将Y表示为X的线性函数，然后利用主成分分析将结果可视化。
在那些可以用X线性解释的Y组分中（多元线性回归）以那些表示大部分方差的成分为例。
=======================================
一组变量(x)如何解释另一组变量(y)
相关分析
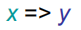单元回归分析
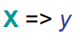
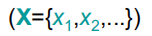多元回归分析
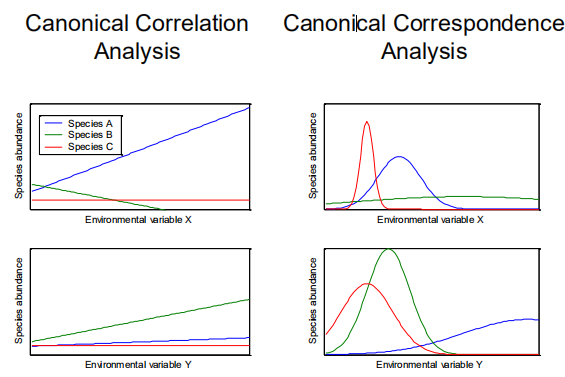
典范相关分析
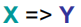冗余分析
====================================
数据集的总方差分为约束和无约束方差，是标准结果。此结果说明您的响应变量有多少变化与解释变量的变化是多余的。
如果约束方差比无约束方差高得多，分析表明，响应数据中的大部分变化可能是由您的解释变量来解释的。 但是，如果有很大比例的无约束变化(即你的反应矩阵中的变化与解释矩阵中的变化无关)，则应谨慎解释结果，因为仅显示了响应矩阵中的少量变化。
关于若干约束轴(RDA轴)和无约束轴(PCA轴)的信息常常出现在RDA的结果中。
点间距离(观测值)观测值的近似距离(或标称解释变量的质心)
响应变量线和解释变量线之间的角度表示关联的二维近似。
其他线间的角度是没有意义的。
点在响应变量直线上的直角投影近似于对应对象沿对应变量的位置。
正方形/三角形不能与定性解释变量线相比较。
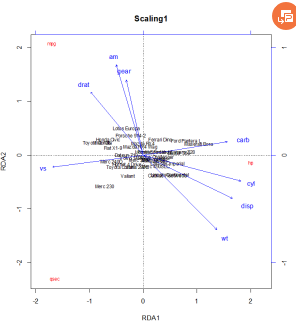
与CA一样，都是xy都做一遍PCA
NMDS是将数值大小转化为排序
典范对应分析CCA
CCA是一种多元约束排序技术，它提取数据集中解释变量组合中的主要梯度。
CCA是通过对应分析来实现的，其中使用加权多元回归将轴表示为解释变量的线性组合。
所以CCA是一个CA，其中轴是说明性变量的线性组合
CCA的要求是样本是随机的和独立的，并且自变量在样本位置内是一致的，并且没有误差。
CCA数据
给定：矩阵Y和X
y[j,i]是i位点的物种数i。
x[j,k]是站点j的自变量k。
目标：寻找物种丰富度和地点的关联
一个站点上的每个环境条件都是X的环境变量的线性组合。
假设：物种的生态位依赖于环境因素。
=========================================
计算步骤
1.从一个卡方物种矩阵[(实际预测)/sqrt(预测)]开始。
2.将环境变量期望的差异回归到拟合值,使用加权回归法，其中以按地块划分的总丰度作为权重。
3.利用特征分析计算拟合物种矩阵和投影的欧氏距离.然后通过它们与投影散点图的相关性来评估特定环境变量的重要性。
三角图
物种评分、地点评分和环境评分都是以一个名为Triplot(RDA中的三幅图)的图形来绘制的。这些三角图是CA的双图，附加的解释变量被绘制成行。
同样，物种的位置代表沿第一和第二轴的高斯响应模型(小生境)的最佳值。因此，物种分数表示为标签或点.
此外：物种可以垂直地(=正交地)投影在显示各自解释变量的物种最优的线上(在各自的标度中)。垂直于这些线的投影点会在这些站点上得到相应的环境变量的值。
线间的角度并不代表变量之间的相关性。 相反，如果一条线的尖端被投影在另一条线或一个轴上，则得到的值表示加权相关性。
======================================================
何时使用PCA、CA、RDA或CCA
- 如果沿梯度的关系是线性的，则应使用PCA分析物种数据
- RDA应用于分析物种和环境变量之间的线性关系。
- CA分析物种数据X和沿梯度y的单峰关系。
- CCA可用于分析物种X矩阵与环境变量Y矩阵之间的单峰关系。
- 如果β多样性较小，或者样本的范围仅覆盖梯度的一小部分，则应使用PCA或RDA。
- 长梯度具有高的β多样性，这表明应当使用CA或CCA。
纯排序|因果关系
===================================================
广义联合属性建模
