数据转换
变换是数值尺度的变化。
变换是对正常、均质、线性和异常值的故障的补救。
数据的标度影响变换的效用。
ü如果标度是任意的,则转换更有效,
如果尺度是有意义的,那么解释的难度就会增加。
===============================
对数变换
因子效应是乘法而不是加法
方差与平均值的平方成正比(即标准差与平均值成正比)
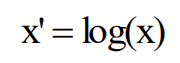
=================================
对数变换实例
假设的方差设计的双向分析,其中因素的影响是加性的(数据以克为单位)。
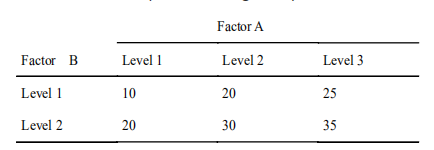
方差设计的假设双向分析,其中因子的影响是乘法的(数据以g表示)。

====================================================
平方根代换
方差与平均值成比例。
泊松分布数据按时间和(或)空间计数,均值等于方差。

=================================
倒数变换
数据组的标准差与组均值的平方成正比。

关于计数数据:
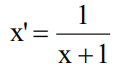
人口密度(单位面积人口)变为人均面积
标准偏差随着组均值的增加而减小,并且/或者如果分布向左倾斜。
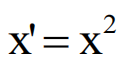
==============================================
反正弦变换
反正弦变换是在处理比例和百分比时帮助数据分析人员的转换。
如果将p的平方根与正弦变换(或反正弦或sin^-1)结合使用,则可使比例p几乎“正态”。
然后,以比例p的函数来计算极谱变换。
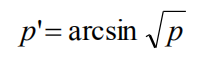
===================================
为什么我们需要正弦变换
二项分布的方差是var(P)=(P)*(1-p)/(n-1)。
p的方差取决于其特定值违反了统计测试计算所需的各学科间方差假设的同质性,例如,如果p被用作方差分析或回归中的因变量。
如果计算出的比例大部分在0.3~0.7之间,则这一变换在分析结果上的差别很小。
然而,使用它是明智的,特别是当大量的观察到的比例是相对较小的(即0<p<0.2)或大(即0.8<p<1.0)。
注:如果大量的比例等于0或1或在p的可能范围的极值处的值,arsin变换就不是特别好。(接近0和接近1)。如果测试次数(即n)很小,也不建议这样做。
=========================================
数据转换
=====================================
方差稳定变换

================================================
不适合转换的数据
在分布的两端有很长的尾巴
具有双峰分布
具有大量相同的观察结果
导致p值变化的变换
==========================================
Box-Cox transformation 略
==============================================



