---恢复内容开始---
生物统计学
古典概型:
理论上,在未得到试验结果之前可以根据实验条件,预先估计出来的所有可能结果称为样本空间,即为集合Ω。样本点w是Ω的一个元素。这是概率的古典定义,即依据事件本身特性,直接得到概率。这里得到的往往是先验概率。

随机事件是一个集合,是样本空间的一个子集。
必然事件是一个集合,包含所有样本点。
不可能事件是一个集合,不包含所有样本点。
Today:
与古典概率的定义不同,现在我们所知的是事物已经发生频率,而通过伯努利大数定律使得大样本的频率约等于概率,这里得到的往往是后验概率。在得知样本分布之后,采用概率论做推论,即prediction。

在已知概率的前提下,对概率进行数理计算得到想要事件发生的概率,就是概率论。
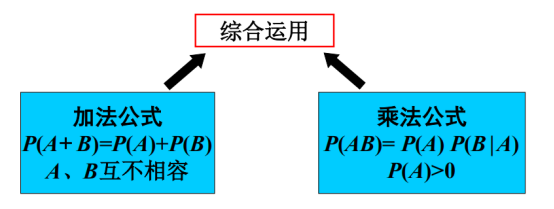
将加法公式和乘法公式综合使用得到全概率公式和贝叶斯公式:
全概率公式由原因(通常已知在A的概率下B发生的概率+A发生的概率)推结果

贝叶斯公式:原因A导致事件B的发生;由结果(某条件下某事件发生概率)推原因(某事件已经发生了,它是由某一原因导致的概率),往往知道结果。
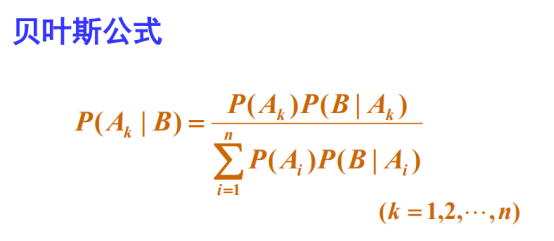
随机变量:
一共有两种类型:
离散型变量:
分布率:当变量是某单一值时有相应的发生概率;
分布函数:当变量是某几个单一值时有相应的发生概率
连续型变量:
概率密度曲线:当变量是某段值时有相应的发生概率
分布函数:当变量是某段值时有相应的发生概率
可以利用以上数学式子计算出参数。
常见的概率分布:
二项分布n,泊松分布很大的时候接近正态分布
泊松分布:稀有事件
正态分布:
显著性水平:0.05

辛钦大数定律:当样本数趋近于无穷时,样本均值与参数均值相等

---恢复内容结束---



