生物统计与实验设计-统计学基础-2&区间估计-1
正态分布参数:均值和方差
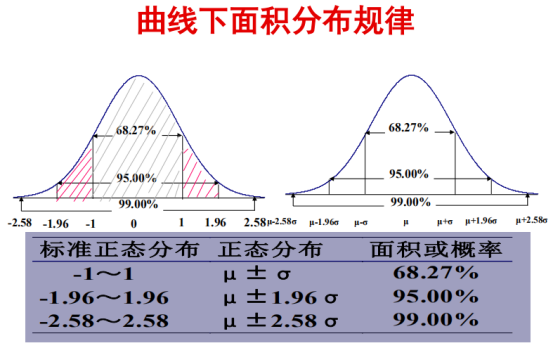
其中,选择1d是因为好算;通常,95%区分大概率事件和小概率事件,
当总体是正态分布时,可以利用常用抽样分布估计出样本参数:
抽样分布是样本估计量是样本的一个函数,在统计学中称作统计量(这就是说,统计量由样本值计算得到),因此抽样分布也是指统计量的分布。以下是当总体满足正态分布时,样本均值也满足正态分布(抽样分布是样本均值的分布,此处是正态分布)样本均值的均值与方差和总体参数之间的关系:
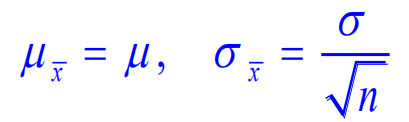
如上式,若得到一次实验的样本,样本容量就是n,计算所有样本会得到一次实验的样本均值,多次实验会得到多次实验的样本均值,假如有600次实验则会得到600个样本均值,再对这600个样本均值进行计算,计算出样本均值的均值和方差,这个样本均值的均值和方差与总体参数满足上式,根据上式关系即可估算出总体均值和总体方差。
当总体不是正态分布,可利用中心极限定理估计出总体参数:
中心极限定理:n足够大则认为样本呈正态分布,因此其样本均数也呈正态分布。
如今,为了精确计算样本均数,存在三种常见的抽样分布(抽样分布是指统计量的分布,以上例为例,就是样本均值的分布),这里的计算是为了得到右边的参数部分。
最为常用的是t分布,它的特点是对于样本含量没有要求:

化简之后是下式:

t分布的期望和方差如下:
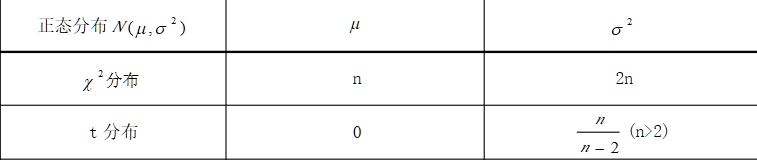
由以上期望和方差可知,t分布只与自由度有关系,与其他无关。
使用t分布作为抽样分布而不使用正态分布的理由是:对于大样本,当n足够大时,t分布和标准正态分布的曲线几乎重合;对于小样本,此时自由度为n-1,并不等同于正态分布(其实若样本容量比较小比如25,样本均值分布很大可能不是正态分布),而t分布在此时因为自由度的控制,使得曲线并非正态分布,比较符合客观事实,所以可以控制系统误差,比标准正态分布更准确。
若不使用t分布,则可以先使用特定数(比如30为界限,此处具体值依据具体问题)判断是大样本或是小样本,再选择分布:
当总体分布为正态分布,则样本指标的分布也 采用正态分布,即用Z分布来进行统计推断。
当总体分布为二项分布(n很大,P有很小), 即当np小于等于5 时,则样本指标的分布采用泊松分布来进行统计推断。反之,当np大于等于5时,可用正态分布近似代替二项分布,则样本指标的分布采用正态分布来进行统计推断。

当小样本时:

以上是通过多个样本得到多个多个统计量再计算均值的方式,后面推出了一个样本便估计参数的方法。

目标是估计出尖值,即估计量:

参数估计可以使用点估计和区间估计,点估计完成了参数估计的从无到有,区间估计完成了参数估计的精细化:
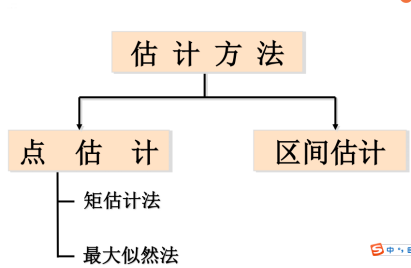
矩估计:提出了用原点矩的方法建立样本矩与总体矩的关系
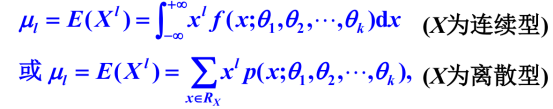
右边是总体矩左边是样本矩:eg,一阶样本矩等于参数均值。所以矩估计的思路是:将总体(含有未知参数的式子,该式子就是由之前学过的不同分布推导或者通用求积分得到)和样本(含有统计量的式子,一般就是数值一个个加或做完处理后一个个加,非常初级)联系起来的桥梁是矩估计
特点:无论总体是出于何种分布(总体矩的表达形式有所不同),最终估计出来的总体参数(仅均值和方差)的表达式完全一致。
最大似然估计是用一组样本估计出总体参数的另一种方法,它的过程是首先建立似然函数,该似然函数是在通过样本得知总体分布之后,结合样本数n,建立在n个样本同时满足某分布之上,得到它们的联合概率密度,取对数(此步骤是为了简化计算,若有其他可化简的方法皆可,它并不参与最大似然的思想)最后对似然函数求最大值(即若估计一个参数求一阶导,和估计两个参数求一阶导和二阶导)。
通过比较矩估计的和最大似然估计的参数,可以得知这一统计量和矩估计量估计出的量是不一定是一样的(但对于总体是正态分布时,估计出的参数是一样的)
经验:先最大似然,再矩估计
在通过以上方式估计参数之后,通过加入估计参数的评判标准,判断何种参数最为可靠:
无偏性:估计的参数满足抽样分布,主要看与集中趋势的比较:若估计的参数是位于所有估计的参数中的集中区域,则认为给估计的参数是无偏的,否则就是有偏的,有偏常常是系统性错误造成的。



