I.9 Linkage
INDEPENDENCE OF GENOTYPES AT TWO LOCI:若A,B是两个独立位点:PA是基因A的概率,PB是基因B的概率。因为基因A与基因B是相互独立的位点,所以基因型AABB的概率为PAABB=(PA)^2*(PB)^2
A RETROSPECTIVE DERIVATION.:
前提一:假设存在两个种群,这两个种群中:A的基因频率PA=1/2、B的基因频率PB=1/2。其中种群1:配子AB和ab各占1/2;种群2:配子Ab,AB,aB,ab各占1/4。因为基因频率不发生改变,所以配子AB的频率一直保持1/4,即PAB=1/4。
前提二:设重组率为r,在第t个世代下,亲代的AB配子频率是PAB。减数分裂过程中存在两种情况:
- 不发生重组:概率为1-r,此时配子中的AB都来自一个亲代(本质上认为C=AB,即配子上的C基因,该基因频率满足哈代公式(因为从亲代到任何一代子代都是随机交配的),所以基因频率不发生改变,所以PAB不发生改变)
- 发生重组:概率为r,配子中的AB分别来自该亲代的上一代,该亲代的上一代的配子频率,就是该亲代的基因频率,所以本质上是计算亲代中基因型为AB的频率PAB,则为PAPB(上一代配子频率相乘)
基于以上分析,得到第一代配子为AB的频率为:
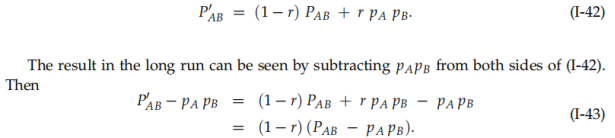
第一代子代配子是AB的频率,即PAB1,即AB发生连锁的频率
亲代配子是AB的频率,即PAB,即AB发生连锁的频率
PAPB是组成AB配子不发生连锁,仅发生重组的频率,所以可以通过此式分析不同世代之间(连锁与重组)的差异,并将这些差异定义为D(t)其中,t为第几世代,所以:
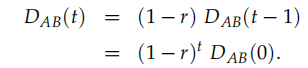
当计算无穷世代时,便令t->正无穷,因为指数函数,底数为小数,当自变量趋近于无穷时,整个函数值趋近于0,所以得到:
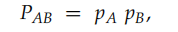
此时基因A与基因B都满足哈代平衡且独立遗传。
所以,最后的平衡称为连锁平衡linkage equilibrium,DAB(t)值称为连锁不平衡参数(linkage disequilibrium)
连锁平衡是在遗传过程中,不同基因座上的等位基因按照随机 原则进行组合时,不同基因座的等位基因组 合的频率等于组合等位基因各自频率的积, 不存在优势组合。这种基因座间没有相关性的状态称为连锁平衡,此时连锁不平衡参数值为0。
连锁不平衡: 在某一群体中,不同座位上某两个等位基因出现在同一条单元型上的频率与预期的随机频率之间存在明显差异的现象,称连锁不平衡
将DAB(t)打开可得到以下表达式:

(1-r)^t代表直到t个世代为止,发生连锁的概率,这些连锁的基因导致了一系列的连锁不平衡。
1-((1-r)^t)代表直到t个世代为止,发生重组的概率
PAB(0)是亲代便是AB连锁的概率
PAPB是AB重组的概率
连锁不平衡现象终会发展为连锁平衡。
进化角度:Recombination gradually scrambles the initial associations of alleles at different loci, until a state of complete randomness is obtained, in which each chromosome is a patchwork of segments derived from different ancestors.
所以,若存在AB基因的连锁平衡,则A基因和B基因是独立遗传,不会相互影响。
SIMPLIFYING POPULATION GENETICS: THE GENE POOL:
如果配子有20个基因座,则配子有2^20种基因型,则组成的二倍体有2^40种基因型,则可区分的基因型有3^20种(eg,原本是四种基因型AA,Aa,aa,Aa,但实际上只有三种基因型,AA,Aa,aa)在连锁平衡之前,配子pool不等于基因pool;在连锁平衡之后,可以通过研究配子基因型(配子pool就是基因pool)来研究二倍体基因型。
A MORE DIRECT DERIVATION:
亲代配子为AB的频率是PAB
则产生ABAB子代的频率是PABAB=PABPAB,该子代产生配子AB的概率是1
分析如下:
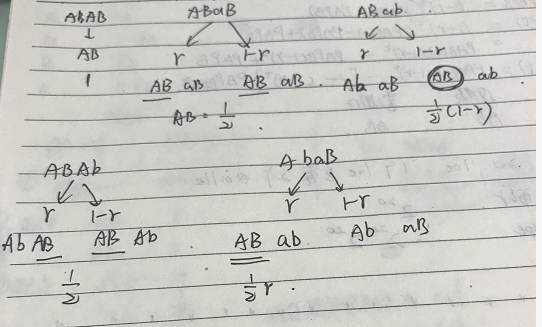
总结后得到:

将产生子代第一代配子为AB的频率总结得到:
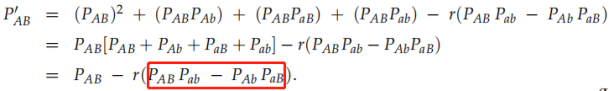
依据配子概率之和为1以及配子的概率关系,得到:
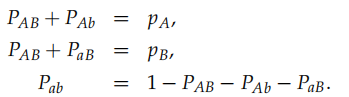
化简:
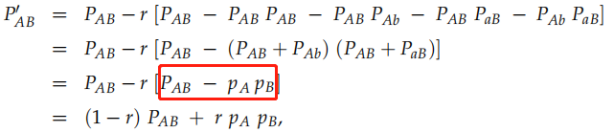
该式说明了第一代子代配子由连锁的亲代配子和重组的配子组成。
显然红框中的式子相等,所以:
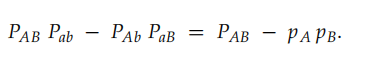
这说明了连锁和重组之间的差异在于双杂合子基因型频率的差异。
因为连锁不平衡参数D被定义为连锁概率-重组概率,所以,对于所有可能配子频率(单体型频率),有如下频率(对于单体型来说是基因型频率)
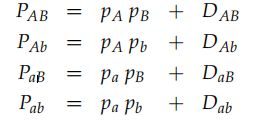
根据式子两两比较,可以得知,
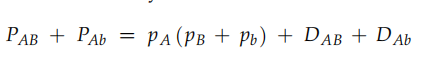
根据基因频率与基因型的关系,可以得知
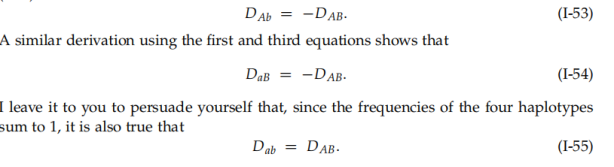
因此,所有不平衡参数可定义为一个变量D,所以:
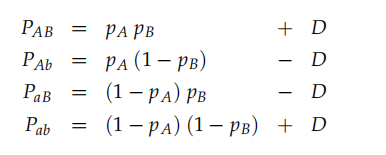
相似的,可以将该等位基因A,a推广到所有等位基因A1A2A3A4……,在不断繁衍过程中,连锁不平衡参数将会不断向0靠近,并且以(1-r)^t的速度靠近0。





