9.24

\(z_1,z_2,z_3,z_4为四个互不相等的复数，|z_i-z_0| = r>0(即共圆)\)
\(求证：\dfrac{z_1-z_3}{z_1-z_4}\dfrac{z_2-z_4}{z_2-z_3}\in R\)

\(情形1:\angle z_4z_1z_3 = \angle z_4z_2z_3即\alpha = \beta\)

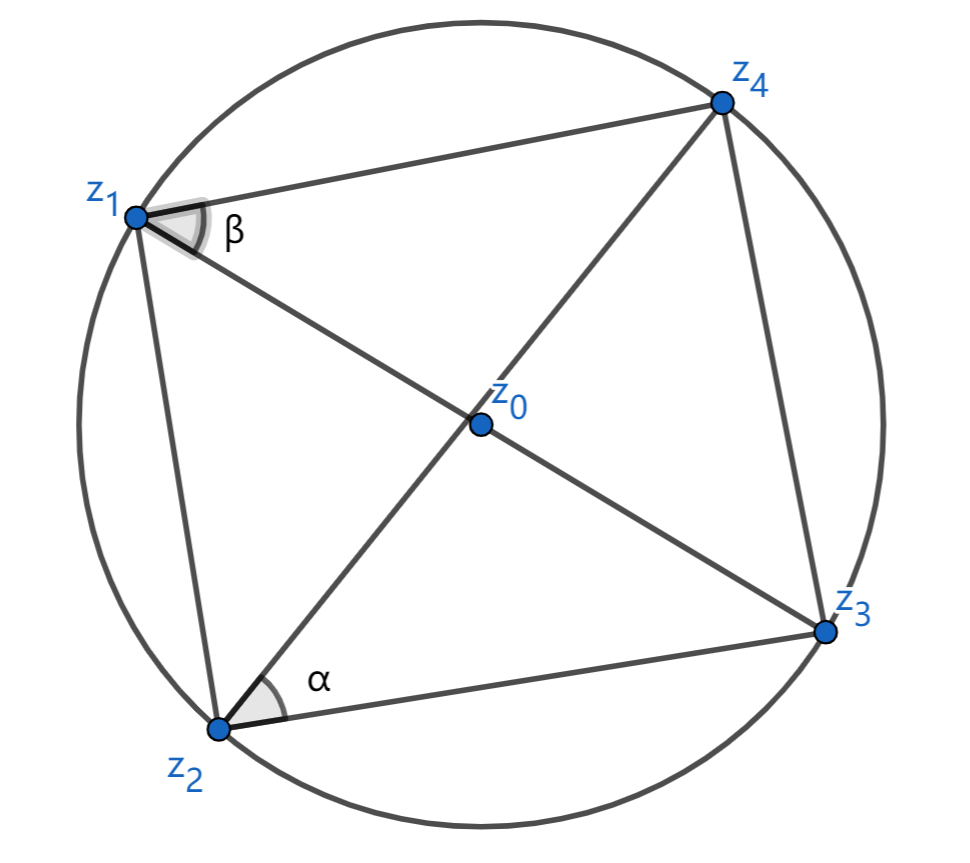
\(如图，有：\)

\[\dfrac{z_4-z_2}{|z_4-z_2|} = \dfrac{z_3-z_2}{|z_3-z_2|}e^{i\alpha} \]

\[\dfrac{z_4-z_1}{|z_4-z_1|} = \dfrac{z_3-z_1}{|z_3-z_1|}e^{i\beta} \]

\(以上二式消去指数部分即得：\)
\(\dfrac{z_1-z_3}{z_1-z_4}\dfrac{z_2-z_4}{z_2-z_3} = \dfrac{|z_1-z_3|}{|z_1-z_4|}\dfrac{|z_2-z_4|}{|z_2-z_3|}\in R^+\)

\(情形2:\alpha+\beta = \pi\)

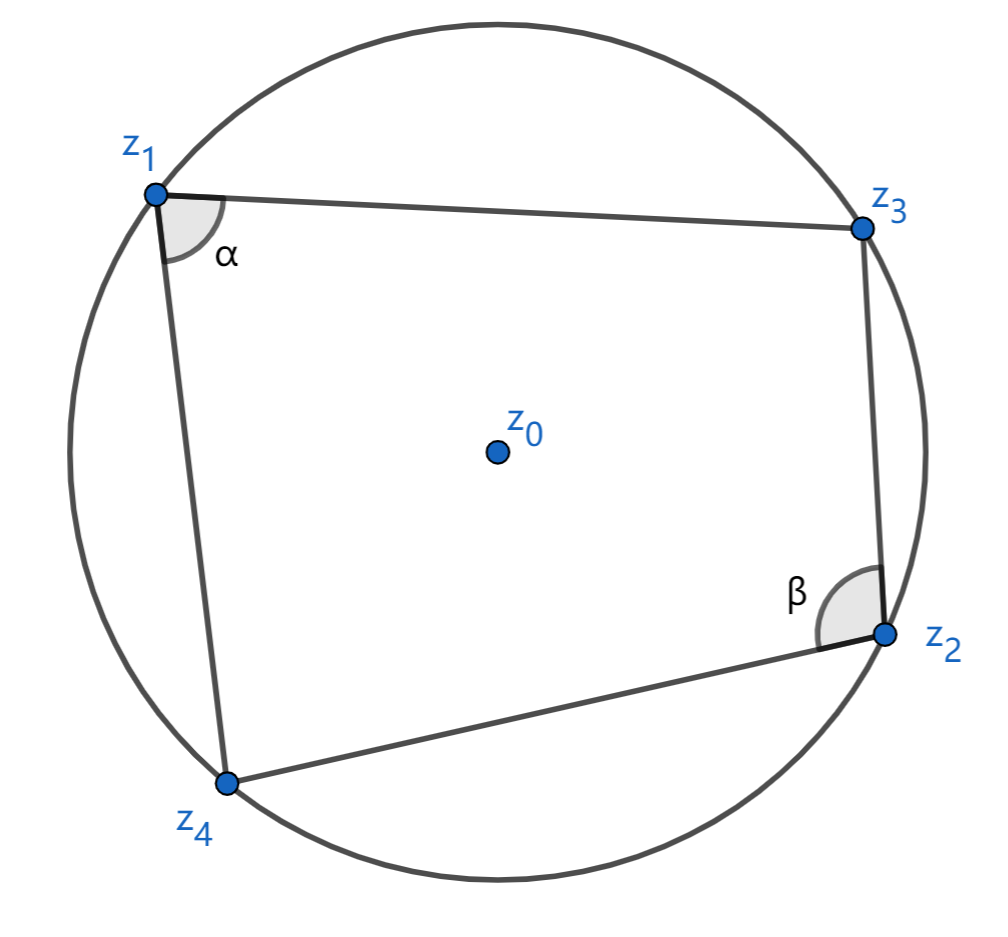
\[\dfrac{z_4-z_2}{|z_4-z_2|} = \dfrac{z_3-z_2}{|z_3-z_2|}e^{i\beta} \]

\[\dfrac{z_4-z_1}{|z_4-z_1|} = \dfrac{z_3-z_1}{|z_3-z_1|}e^{-i\alpha} \]

\(以上二式消去指数部分(e^{i\pi} = -1)即得：\)
\(\dfrac{z_1-z_3}{z_1-z_4}\dfrac{z_2-z_4}{z_2-z_3} = -\dfrac{|z_1-z_3|}{|z_1-z_4|}\dfrac{|z_2-z_4|}{|z_2-z_3|}\in R^-\)

\(综上：\dfrac{z_1-z_3}{z_1-z_4}\dfrac{z_2-z_4}{z_2-z_3}\in R\)