Anal 21-22 甲
2021-2022数学分析(甲)I期末考试
\(1.计算题\)
\((1)写出sinx带拉格朗日余项的麦克劳林展开式.\)
\(sinx = x-\dfrac{1}{6}x^3+\dfrac{1}{5!}x^5+...+(-1)^n\dfrac{cos\theta x}{(2n+1)!}x^{2n+1},0<\theta<1\)
\((2)\lim\limits_{x\to 0}\dfrac{(1+x)^{\frac{1}{x}}-e}{x}\)
?\(\lim\limits_{x\to 0}\dfrac{(1+x)^{\frac{1}{x}}-e}{x} = \lim\limits_{x\to 0}e·\dfrac{e^{\frac{ln(x+1)}{x}-1}-1}{x} = \lim\limits_{x\to 0}e\dfrac{ln(x+1)-x}{x^2} = -\dfrac{e}{2}\)
\(注:幂指函数化e底+等价无穷小+泰勒\)
\((3)\int (x^2+1)^2dx\)
\(\int (x^4+2x^2+1)dx = \dfrac{1}{5}x^5+\dfrac{2}{3}x^3+x+C\)
\((4)\int \dfrac{ln^2x}{x}dx\)
\(原式 = \int ln^2xd(lnx) = \dfrac{1}{3}ln^3x+C\)
\((5)\int arcsin\sqrt{\dfrac{x}{1+x}}dx\)
\(原式 = xarcsin\sqrt{\dfrac{x}{1+x}} - \int x\dfrac{1}{\sqrt{1-\dfrac{x}{1+x}}}\dfrac{1}{2\sqrt{\dfrac{x}{1+x}}}\dfrac{1}{(1+x)^2}dx = xarcsin\sqrt{\dfrac{x}{1+x}} - \int \dfrac{\sqrt {x}}{2(1+x)}dx = xarcsin\sqrt{\dfrac{x}{1+x}} - \sqrt{x}+arctan\sqrt{x}+C\)
\((6)\int \dfrac{1}{(x+1)(x^2+1)}dx\)
\(原式 = \dfrac{1}{2}\int (\dfrac{1}{x+1}+\dfrac{1-x}{1+x^2})dx = \dfrac{1}{2}ln|1+x|-\dfrac{1}{4}ln(1+x^2)+\dfrac{1}{2}arctanx+C\)
\(2.f在[0,1]上满足:\exists L>0,\forall x,y\in [0,1],有|f(x)-f(y)|\le L|x-y|,求证:f在[0,1]上一致连续.\)
\(\forall \epsilon>0,\exists \delta,\forall x',x''\in[0,1],只要|x'-x''|<\delta,就有|f(x')-f(x'')|\le L|x'-x''|\le L\delta.\)
\(故只需要取\delta = \dfrac{\epsilon}{L}\)
\(3.已知\forall x_1,x_2,x_3\in(0,1),x_1<x_2<x_3,有\dfrac{f(x_1)-f(x_2)}{x_1-x_2}\le \dfrac{f(x_2)-f(x_3)}{x_2-x_3}\)
\(证明:(1)\forall x_0\in (0,1),f'_-(x_0)和f'_+(x_0)存在\)
\(先证明:\dfrac{f(x_1)-f(x_2)}{x_1-x_2}\le \dfrac{f(x_2)-f(x_3)}{x_2-x_3}和\dfrac{f(x_1)-f(x_2)}{x_1-x_2}\le \dfrac{f(x_1)-f(x_3)}{x_1-x_3}等价,事实上,去分母整理即证.\)
\(对(0,1)内四点x_1<x_2<x_0<x_3,有:\dfrac{f(x_1)-f(x_0)}{x_1-x_0}\le \dfrac{f(x_2)-f(x_0)}{x_2-x_0}\le \dfrac{f(x_0)-f(x_3)}{x_0-x_3}\)
\(设g(x) = \dfrac{f(x)-f(x_0)}{x-x_0},则g(x)在(0,x_0)上递增,并且g(x)有上界\dfrac{f(x_0)-f(x_3)}{x_0-x_3}\)
\(由函数单侧极限存在的单调有界收敛准则:\lim\limits_{x\to x_0^-}g(x)存在即f'_-(x_0)存在,同理右导数存在.\)
\((2)f'_-(x_0)\le f'_+(x_0)\)
\(对x-h,x,x+h三点由题干中的不等式:\dfrac{f(x-h)-f(x)}{-h}\le\dfrac{f(x+h)-f(x)}{h}令h\to 0^+即得\)
\((3)f'_-(x),f'_+(x)在(0,1)上递增.\)
\(\forall 0<x_1<x<y<x_2<1有:\dfrac{f(x_1)-f(x)}{x_1-x}\le\dfrac{f(x)-f(y)}{x-y} \le\dfrac{f(x_2)-f(y)}{x_2-y}\)
\(令x\to x_1^+,y\to x_2^-,得:f'_+(x_1)\le f'_-(x_2)\)
\(结合(2)得f'_-(x_1)\le f'_+(x_1)\le f'_-(x_2)\le f'_+(x_2)\)
\(所以左右导数都单调增加.\)
\(提示:此题揭示下凸(或上凸)函数的等价定义和基本性质:单侧导数存在性,单侧导数的单调性.\)
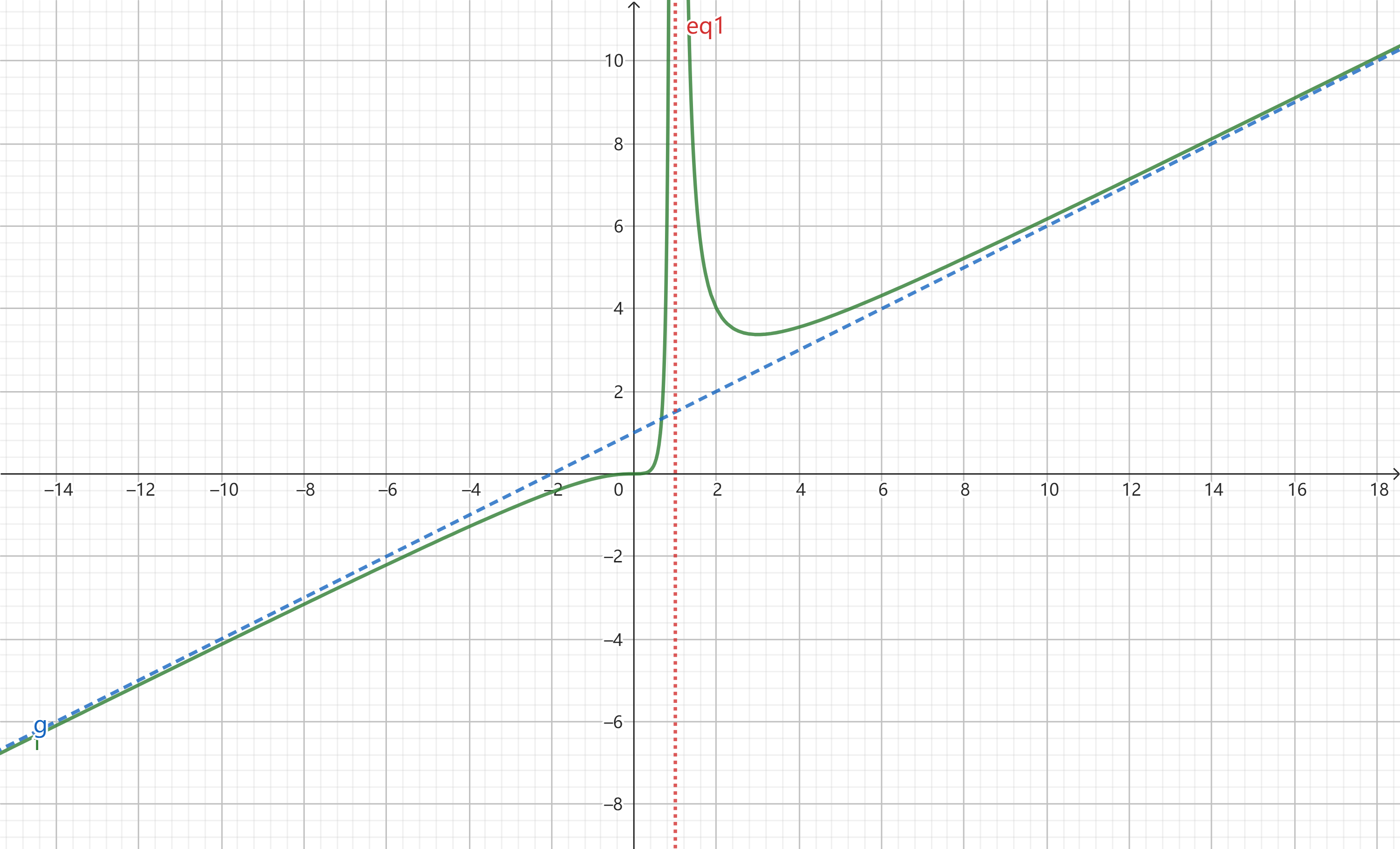
\(4.作图:y = \dfrac{x^3}{2(x-1)^2}\)
\(渐近线y = \dfrac{1}{2}x+1, x = 1,极值点x=3,拐点(0,0)\)
\(5.已知\forall h>0,\forall x\in R,有|f(x)|\le M_0,|f''(x)|\le M_2\)
\((1)写出f(x+h)和f(x-h)在x处的二阶泰勒展开式\)
\((2)证明:|f'(x)|\le\dfrac{M_0}{h}+\dfrac{hM_2}{2}\)
\((3)求\dfrac{M_0}{h}+\dfrac{hM_2}{2}的最小值\)
\((4)证明:|f'(x)|\le\sqrt{2M_0M_2}\)
助教习题课讲过,我在此处贴个答案