力扣刷题

你们总在悲痛或需要的时候祈祷,我愿你们也在完满的欢乐中及丰富的日子里祈祷。 ——《先知》纪伯伦

力扣刷题

简单难度

[1] 两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

nums = [2, 7, 11, 15]

target = 9

返回 [0, 1]

解法一：

枚举一个数x，再通过遍历剩下数组来寻找 target-x

第一个循环中，i 从 0 开始，到 n-2 结束
第二次循环中，i 从 i+1 开始，到 n-1 结束

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (nums[i] + nums[j] == target) {
                    return new int[]{i, j};
                }
            }
        }
        return new int[0];
    }
}

解法二：

使用 HashMap，将 nums[i]作为键，i作为值。

好处是：可以使用 map.containsKey方法判断 target-value 是否在已有的 map中存在

注意：在添加数据时，应先进行判断。好处是：可以避免出现自己+自己 = target的情况

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        for (int i = 0; i < nums.length; ++i) {
            int ano = target - nums[i];
            if (map.containsKey(ano)) {
                return new int[]{map.get(ano), i};
            }
            map.put(nums[i], i);
        }
        return new int[0];
    }
}

[7] 整数反转

给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

输入: 123

输出: 321

输入: -123

输出: -321

输入: 120

输出: 21

注意:

假设我们的环境只能存储得下 32 位的有符号整数，则其数值范围为 [−231, 231 − 1]。请根据这个假设，如果反转后整数溢出那么就返回 0。

解法一：

将数字中的每一位都单独取出来放到集合中，然后再对每一位数字进行拼接，拼成反转后的数字。

此时需要注意：拼接的时候判断数字是否会超出 int数的上限，因此需要在拼之前判断。

class Solution {
    public int reverse(int x) {
        if (x == Integer.MAX_VALUE || x == Integer.MIN_VALUE) return 0;
        boolean flag = x > 0 ? true : false;
        LinkedList<Integer> list = new LinkedList<>();
        x = Math.abs(x);
        while (x / 10 > 0) {
            list.add(x % 10);
            x = x / 10;
        }
        list.add(x);

        int answer = 0;
        // System.out.println(list);
        while (!list.isEmpty()) {
            int pop = list.pop();

            // System.out.println(pop);

            if (answer > (Integer.MAX_VALUE / 10)) {
                return 0;
            } else if (answer == (Integer.MAX_VALUE / 10) && pop > 7) {
                return 0;
            }

            answer = (answer * 10) + pop;

        }

//        return answer;
        return flag == true ? answer : -answer;
    }
}

解法二：

边获取每个位置的数，边拼接，只需要一次循环即可

class Solution {
    public int reverse(int x) {
        // 定义反转后的数的值
        int rev = 0;
        while (x != 0) {
            // 削下来一位数
            int pop = x % 10;
            // 改变原数
            x /= 10;
            // 判断拼接否是否会溢出
            if (rev > Integer.MAX_VALUE/10 || (rev == Integer.MAX_VALUE / 10 && pop > 7)) return 0;
            if (rev < Integer.MIN_VALUE/10 || (rev == Integer.MIN_VALUE / 10 && pop < -7)) return 0;
            // 数字拼接
            rev = rev * 10 + pop;
        }
        return rev;
    }
}

[20] 有效括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合；
左括号必须以正确的顺序闭合
空字符串可被认定为有效字符串

输入: "()"
输出: true

输入: "()[]{}"
输出: true

输入: "(]"
输出: false

解法一

使用 Java栈 Stack来统计括号信息，如果是左括号，就入栈，如果是右括号就弹栈，并进行判断

如果整个字符串遍历完，且遍历期间每次弹栈判断都是括号匹配的，就返回 true；

否则，如果栈未空，或存在某次不匹配，就返回 false

class Solution {
    public boolean isValid(String s) {
        char[] chars = s.toCharArray();
        // 如果是奇数个，那么肯定不匹配
        if (chars.length % 2 == 1) {
            return false;
        }
        Stack<Character> stack = new Stack<>();
        for (Character character : chars) {
            if (character == '{' || character == '[' || character == '(') {
                stack.push(character);
                continue;
            }
            if (!stack.isEmpty()) {
                if (character == '}' && stack.pop() != '{') {
                    return false;
                }

                if (character == ']' && stack.pop() != '[') {
                    return false;
                }

                if (character == ')' && stack.pop() != '(') {
                    return false;
                }
            } else {
                return false;
            }

        }
        if (!stack.isEmpty()) {
            return false;
        }
        return true;
    }
}

解法二

和解法一差不多，只是入栈的内容变成了右括号，另外整体的编码风格较好

class Solution {
    public boolean isValid(String s) {
        if(s.isEmpty()) {
            return true;
        }
        Stack<Character> stack = new Stack<>();
        for(Char c : s.toCharArray()) {
            if(c == '{') {
                stack.push('}');
            } else if(c == '[') {
                stack.push(']');
            } else if(c == '(') {
                stack.push(')');
            } else if(stack.isEmpty() || c != stack.pop()) {
                return false;
            }
        }
       
        return stack.isEmpty();
    }
}

解法三

使用 HashMap和 LinkedList求解

class Solution {
    public boolean isValid(String s) {
        int n = s.length();
        if(n % 2 == 1) {
            return false;
        }
        Map<Character, Character> paris = new HashMap<>();
        paris.put(')', '(');
        paris.put(']', '[');
        paris.put('}', '{');
        
        Deque<Character> stack = new LinkedList<>();
        for(int i = 0; i < n; i++) {
            char ch = s.charAt(i);
            if(paris.containsKey(ch)) {
                if(stack.isEmpty || stack.peek() != paris.get(ch)) {
                    return false;
                }
                stack.pop();
            } else {
                stack.push(ch);
            }
        }
        return stack.isEmpty();
    }
}

[21] 合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

输入：l1 = [], l2 = []
输出：[]

输入：l1 = [], l2 = [0]
输出：[0]

解法一：

参考严蔚敏《数据结构》书中的写法，注意这里的 l1 和 l2是没有头结点的

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {

        ListNode p = l1, q = l2;
        ListNode dummy = new ListNode(), cur = dummy;

        while(p != null && q != null) {
            if (p.val >= q.val) {
                cur.next = q;
                q = q.next;
            } else {
                cur.next = p;
                p = p.next;
            }
            cur = cur.next;
        }

        cur.next = p == null ? q : p;

        return dummy.next;
    }
}

解法二

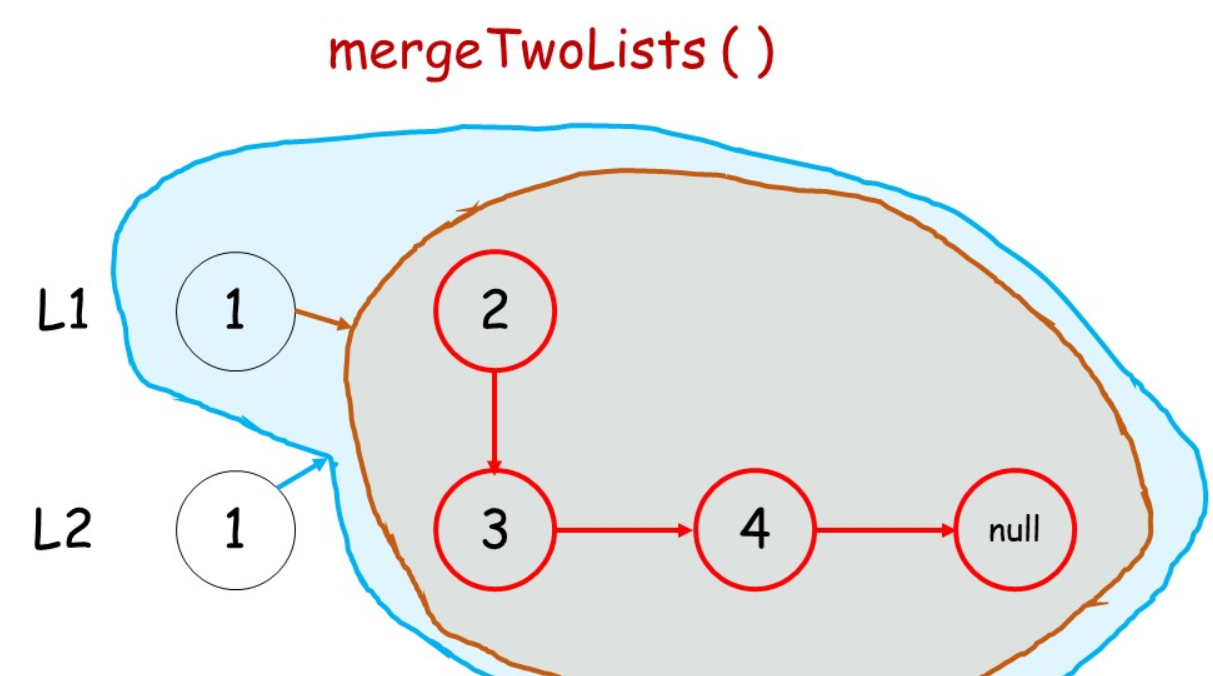
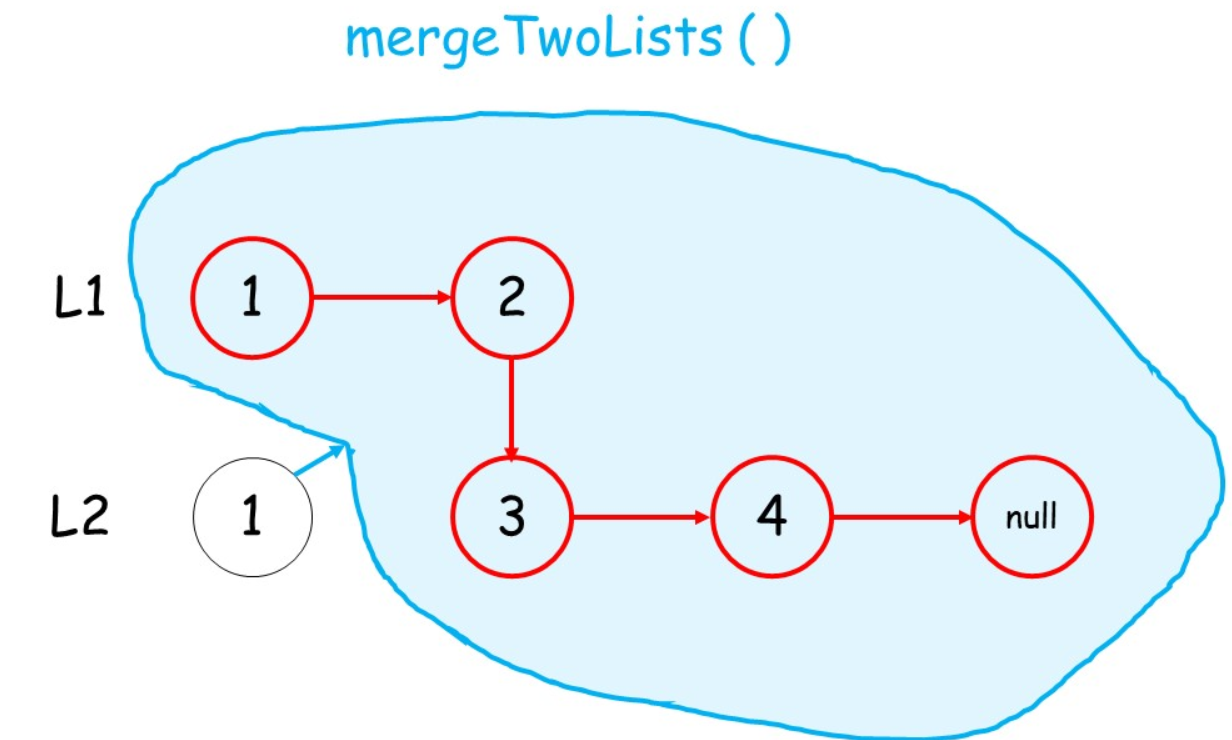
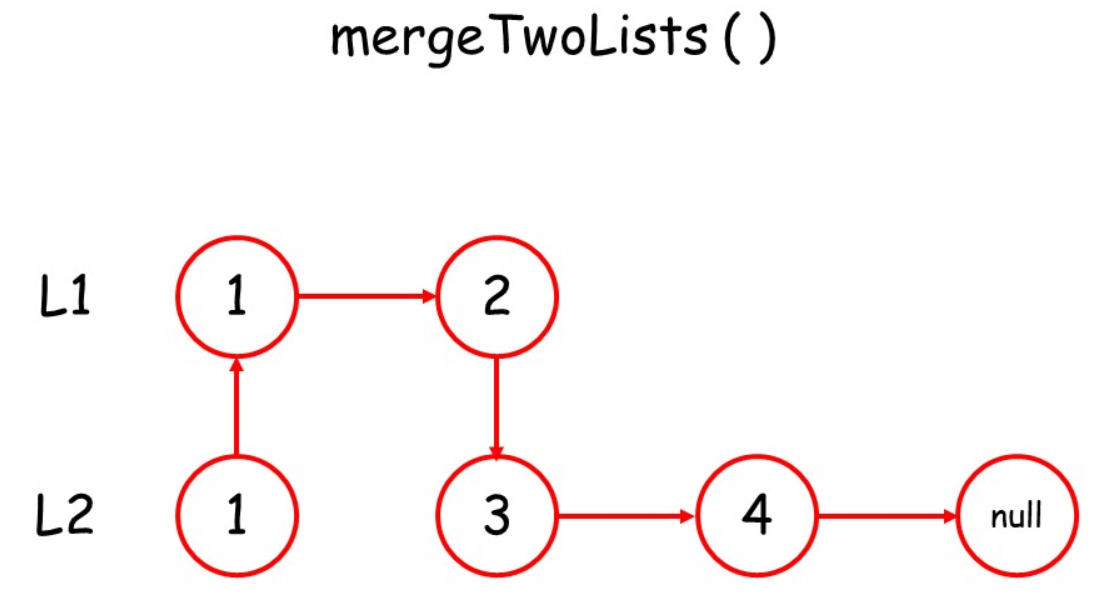
采用递归

终止条件：当两个链表都为空后，表示我们对两个链表的合并已完成

如何递归：判断两个链表的结点哪个更小，然后较小结点的 next指针指向其余结点的合并结果

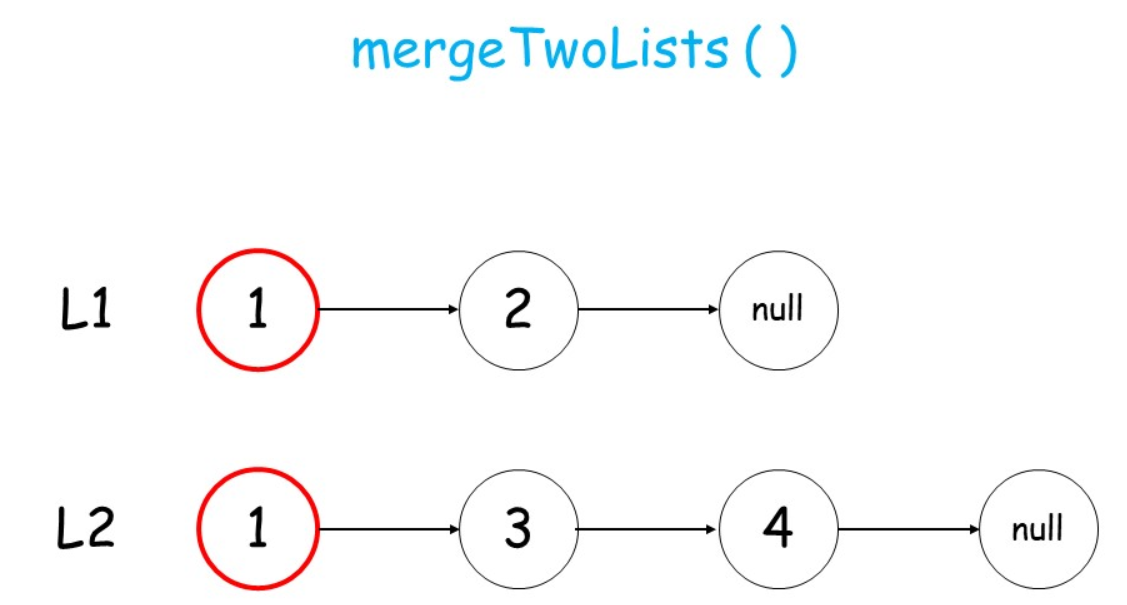
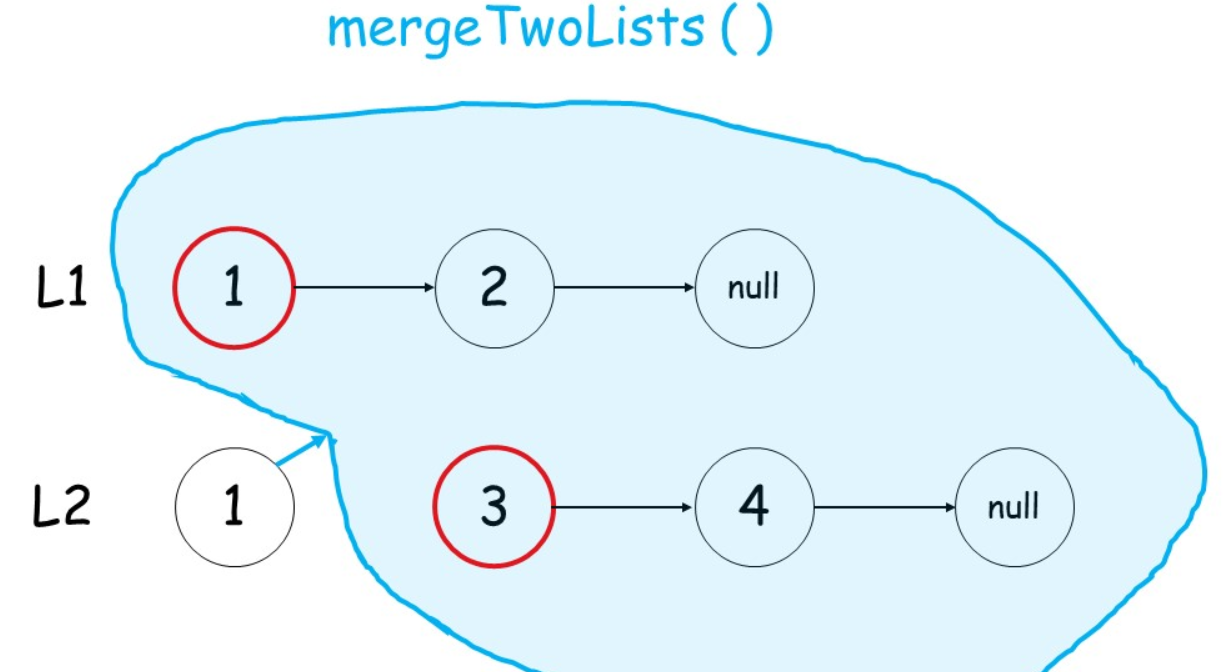
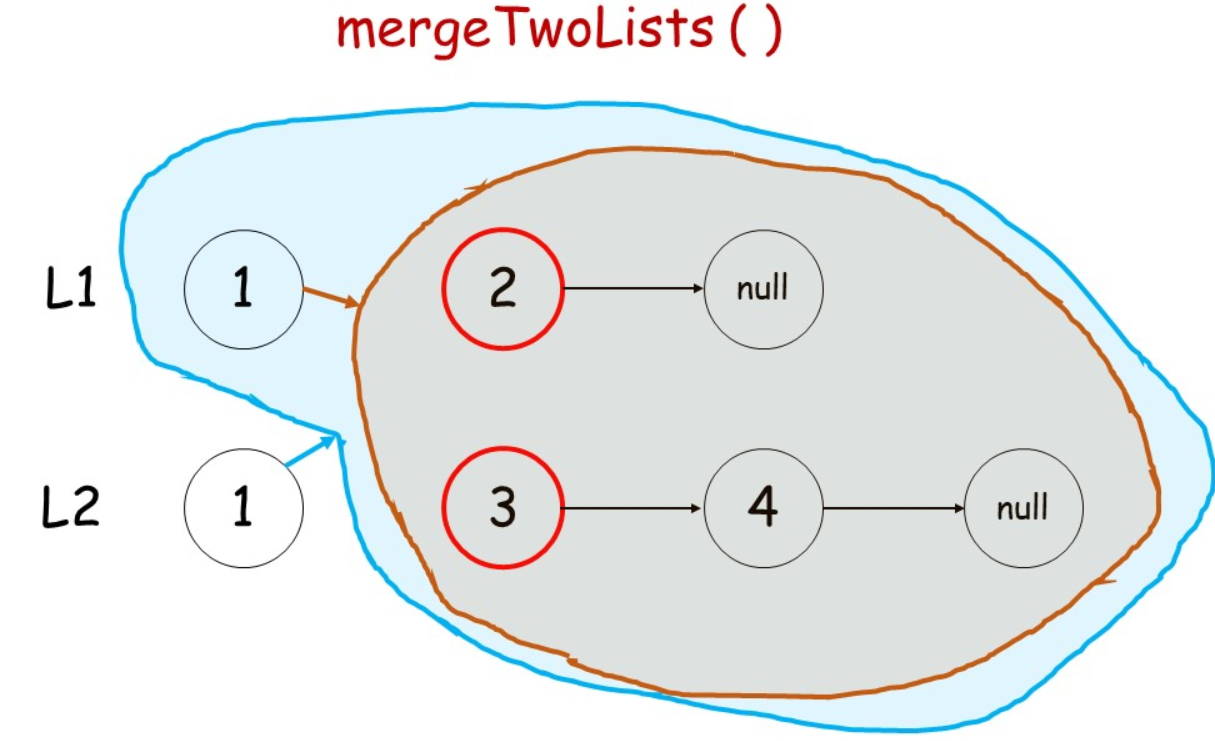
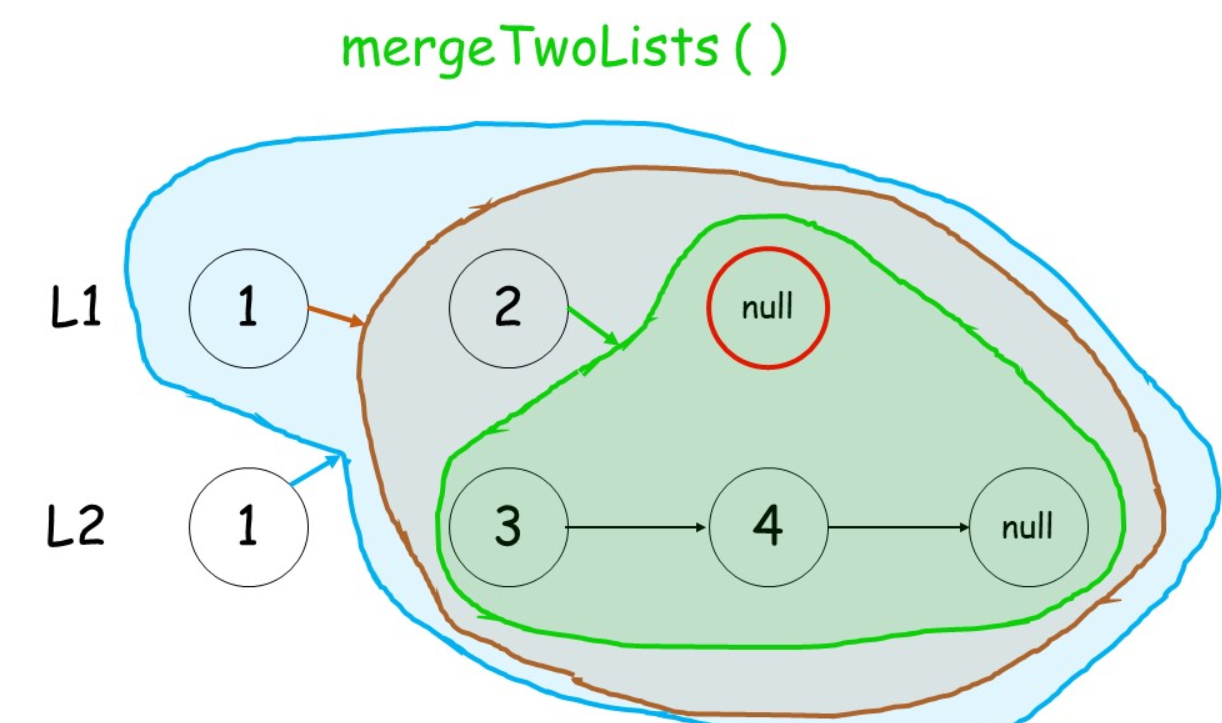
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        } else if (l2 == null) {
            return l1;
        }

        if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

[26] 删除有序数组中的重复项

给你一个有序数组 nums ，请你原地删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

0 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列

Related Topics

数组

双指针

解法一：

快慢指针

注意这里需要返回处理后数组的长度，因此可以使用 slow+1来返回

并且，数组元素的去重操作可以直接使用拷贝的方式进行元素覆盖，并且只要拷贝一个过来就行

class Solution {
    public int removeDuplicates(int[] nums) {

        if (nums.length <= 1) {
            return nums.length;
        }

        int slow = 0, fast = 0;

        while (fast < nums.length) {
            /*
            如果快慢指针的值不同，就把新的值赋给原来 slow后面一个，因为数组是有序的所以某个元素的重复值都是聚在一起的
            注意，这里只需要复制过来一个就行了，不需要把后半个数组全部拷贝过来
            因为 fast++是在循环的最后执行，因此前面的操作都不用担心 fast越界
            */
            if (nums[fast] != nums[slow]) {
                slow++; // 必须先 slow++，再进行赋值操作
                nums[slow] = nums[fast];
            }

            // 不管值是不是一样的，fast都会后移一位
            fast++;
        }

        // slow是数组的下标，如果用它来表示数组的长度的话，需要 +1
        return slow + 1;
    }
}

第三次刷题的时候手写：

class Solution {
    public int removeDuplicates(int[] nums) {
        int slow = 0, fast = slow+1;
        while(fast < nums.length) {
            if (nums[fast] == nums[slow]) {
                fast++;
                continue;
            }
            nums[++slow] = nums[fast];
            fast++;
        }
        return slow+1;
    }
}

[27] 移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

Related Topics

数组

双指针

解法一：

双指针

基本同上一题

class Solution {
    public int removeElement(int[] nums, int val) {

        /*
        每次都重新赋值一次值
            将 nums[fast]的值赋值给 nums[slow]
            除非遇到 nums[fast]的值等于 val的情况，这个时候就直接 fast++，不赋值了
            到最后时，0~slow就是被保留下来的数组元素了
         */

        int slow = 0, fast = 0;
        while (fast < nums.length) {
            if (nums[fast] != val) {
                nums[slow] = nums[fast];
                slow++;
            }
            fast++;
        }
        // 因为每次遍历的时候，都会有一次 slow++，所以最后实际上 slow就是数组的有效元素的长度了
        return slow;
    }
}

♥ [28] 实现 strStr()

实现 strStr() 函数。

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

说明：

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。

示例 1：
输入：haystack = "hello", needle = "ll"
输出：2
示例 2：
输入：haystack = "aaaaa", needle = "bba"
输出：-1
示例 3：
输入：haystack = "", needle = ""
输出：0
提示：

0 <= haystack.length, needle.length <= 5 * 104

haystack 和 needle 仅由小写英文字符组成

Related Topics

双指针

字符串

字符串匹配

解法一：

暴力枚举

遍历原字符串，从该字符开始，向后与待比较字符串进行匹配；

匹配成功，则返回开始匹配的字符位置；否则该字符后移一位

复杂度为 O(m*n)

class Solution {
    public int strStr(String haystack, String needle) {

        if (needle == null || needle.isEmpty()) {
            return 0;
        }

        int n = haystack.length(), m = needle.length();
        char[] s = haystack.toCharArray(), p = needle.toCharArray();

        for (int i = 0; i <= n - m; i++) {
            int a = i, b = 0;

            // 逐位比较
            while (b < m && s[a] == p[b]) {
                a++;
                b++;
            }

            // 检查一下是不是都匹配上了
            if (b == m) {
                return i;
            }
        }
        return -1;
    }
}

❤ 解法二：

KMP

背下来

next[]数组记录了模式串和主串不匹配时，模式串应该从哪里开始重新匹配

当我们找到不匹配的位置时，需要看它的前一个字符的 next[]数组记录的数值是多少

忘记的时候就看视频把

class Solution {
    public int strStr(String haystack, String needle) {
        if (needle == null || needle.isEmpty()) {
            return 0;
        }

        int n = haystack.length(), m = needle.length();

        // 原串和匹配串前面都加空格，使其下标从 1开始
        // 如果不加 " "，那么下面循环的时候需要设定 i=1, j=-1
        haystack = " " + haystack;
        needle = " " + needle;
        char[] s = haystack.toCharArray(), p = needle.toCharArray();

        // 构建 next数组，其长度为匹配串长度
        int[] next = new int[m + 1];
        // 遍历匹配串
        for (int i = 2, j = 0; i <= m; i++) {

            // 如果前后缀匹配不成功，进行回溯
            while (j > 0 && p[i] != p[j + 1]) {
                j = next[j];
            }

            // 匹配成功的话，先让 j++
            if (p[i] == p[j + 1]) {
                j++;
            }

            // 将 j赋值给 next[i]，来记录其前后缀的长度
            next[i] = j;
        }

        // 匹配过程
        for (int i = 1, j = 0; i <= n; i++) {

            // 如果匹配不成功，j = next[j]
            while (j > 0 && s[i] != p[j + 1]) {
                j = next[j];
            }

            // 如果，字符串和匹配串的当前字符，匹配成功
            if (s[i] == p[j + 1]) {
                j++; // i++在 for循环里
            }

            // 当 j指向模式串的末尾时，就表示已经完成了匹配
            if (j == m) {
                // 找出模式串中字符串出现的第一个位置
                return i - m;
            }
        }

        return -1;
    }
}

[34] 在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：

你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

示例 1：
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]
示例 2：
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]
示例 3：
输入：nums = [], target = 0
输出：[-1,-1]
提示：

0 <= nums.length <= 105

-109 <= nums[i] <= 109

nums 是一个非递减数组

-109 <= target <= 109

Related Topics

数组

二分查找

解法一：

先二分查找找到一个对应 target数的位置，然后向上向下逐个比较获取位置。

这个时候其实就会从 O(logN) 退化到 O(N)了

解法二：

直接通过二分找到上下两个边界，但是要二分两次

解析详见 day5:二分搜索原理

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] arr = new int[2];
        arr[0] = searchLeft(nums, target);
        arr[1] = searchRight(nums, target);
        return arr;
    }

    public int searchLeft(int[] nums, int target) {
        int left = 0, right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (nums[mid] == target) {
                right = mid - 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            }
        }
        if (left >= nums.length || nums[left] != target) {
            return -1;
        }
        return left;
    }

    public int searchRight(int[] nums, int target) {
        int left = 0, right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            System.out.println("right: " + mid);

            if (nums[mid] == target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            }
        }

        if (right < 0 || nums[right] != target) {
            return -1;
        }
        return right;
    }
}

前闭后开的版本

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] arr = new int[2];
        arr[0] = searchLeft(nums, target);
        arr[1] = searchRight(nums, target);
        return arr;
    }

    public int searchLeft(int[] nums, int target) {
        int left = 0, right = nums.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid;
            }
        }
		// 无论是找左边界还是有边界，都应当注意跳出循环时的具体条件是什么
        // 像这里就是 left == right(二者都是一个一个加减的，所以一定是在相等的时候退出循环)
        // 假设数组为 [2, 2]，target = 3，你找左边界，那么这个左边界找出来就是 2(不存在)，因此需要做出如下判断
        if (left >= nums.length || nums[left] != target) {
            return -1;
        }

        return left;
    }

    public int searchRight(int[] nums, int target) {
        int left = 0, right = nums.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            }

        }

        // 同上，针对 [2, 2] target=1，找右边界，找出来的就是 -1(right - 1 = -1, right = 0)
        if (right <= 0 || nums[right - 1] != target) {
            return -1;
        }

        return right - 1;
    }
}

[66] 加一

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1：
输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。
示例 2：
输入：digits = [4,3,2,1]
输出：[4,3,2,2]
解释：输入数组表示数字 4321。
示例 3：
输入：digits = [0]
输出：[1]
提示：

1 <= digits.length <= 100

0 <= digits[i] <= 9

Related Topics

数组

数学

解法一：

先对 digits[]中的最后一个元素加一
从尾部遍历到头部，判断 digit[i] >= 10，如果是的话，digit[i] -= 10，同时 digit[i-1] += 1
最后判断头部digit[0]，如果digit[0] >= 10的话，就需要再向前进位，但此时数组不够大了，所以需要新建数组

class Solution {
    public int[] plusOne(int[] digits) {
        int len = digits.length;
        // 先处理尾巴
        digits[len - 1] += 1;

        // 倒着遍历数组
        for (int i = digits.length - 1; i > 0; i--) {
            if (digits[i] >= 10) {
                digits[i] -= 10;
                digits[i - 1] += 1;
            }
        }

        // 判断 digits[0]的情况
        if (digits[0] >= 10) {
            int[] res = new int[digits.length + 1];
            digits[0] -= 10;
            res[0] = 1;
            System.arraycopy(digits, 0, res, 1, digits.length);
            return res;
        }

        return digits;
    }
}

优化需要进位的情况

class Solution {
    public int[] plusOne(int[] digits) {
        final int len = digits.length;
        digits[len - 1] += 1;

        for (int i = len - 1; i > 0; i--) {
            if (digits[i] >= 10) {
                digits[i] -= 10;
                digits[i - 1] += 1;
            }
        }

        if (digits[0] >= 10) {
            digits[0] -= 10;
            // 当需要增加一位的时候，原数组一定是类似 9999这种，所以加一以后才会产生进位，且进位后结果一定是 10000这种
            // 那么只要新建一个数组，让第一个元素变成 1就行了，其他反正默认就是 0
            digits = new int[len + 1];
            digits[0] = 1;
        }

        return digits;
    }
}

[70] 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

Related Topics

记忆化搜索

数学

动态规划

解法一：

构造数组 int[] dp = new int[n+1]，dp[i]即爬到第 i级台阶可能的数量

根据题干，可得 状态转移方程

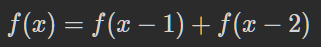
class Solution {
    public int climbStairs(int n) {
        if (n < 2) {
            return n;
        }

        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i < dp.length; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        return dp[n];
    }
}

优化

不维护整个数组，只维护两个值

class Solution {
    public int climbStairs(int n) {
        if (n < 2) {
            return n;
        }

        int p = 1, q = 1;
        for (int i = 2; i < n + 1; i++) {
            int sum = 0;
            sum = p + q;
            p = q;
            q = sum;
        }

        return q;
    }
}

[83] 删除排序链表中的重复元素

存在一个按升序排列的链表，给你这个链表的头节点 head ，请你删除所有重复的元素，使每个元素只出现一次。

返回同样按升序排列的结果链表。

也就是说，如果某个元素重复了，就只保留一个，删掉多余的。

示例 1：

输入：head = [1,1,2]
输出：[1,2]

示例 2：

输入：head = [1,1,2,3,3]
输出：[1,2,3]

提示：

链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序排列

解法一：

双指针遍历链表

快指针每次向后迭代一次；慢指针当出现两个指针的 val值相同时不动，但是每次移动时都会修改其 next指针域指向快指针

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null) {
            return head;
        }

        // cur代表当前节点，next代表下一个结点
        ListNode cur = head, next = cur.next;
        while (next != null) {
            // 如果下一个结点的值同当前节点的值相同，就再向下遍历
            if (cur.val == next.val) {
                next = next.next;
                continue;
            }

            // 使当前节点的 next域指向第一个不重复的节点
            cur.next = next;
            cur = next;
            next = next.next;
        }
        // 存在一种情况：链表最后的几个节点值重复，此时可以直接把 cur.next设置为 null，别的啥都不用管了
        cur.next = null;

        return head;
    }
}

解法二：

借用栈来替代双指针中的慢指针

[88] 合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：
输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。
示例 2：
输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3：
输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示：

nums1.length == m + n

nums2.length == n

0 <= m, n <= 200

1 <= m + n <= 200

-109 <= nums1[i], nums2[j] <= 109

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

Related Topics

数组

双指针

排序

解法一：

先把所有 nums2中的元素都添加到 nums1中，之后再对 nums1进行排序

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        if (n == 0) {
            return;
        }

        System.arraycopy(nums2, 0, nums1, m, n);
        Arrays.sort(nums1);
    }
}

解法二：

不使用 JavaAPI，创建一个临时数组 tmp，遍历 nums1 和 nums2中的两个元素，扔到 tmp中

最后再把 tmp中的元素扔回 nums1中

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {

        int[] tmp = new int[m + n];
        int i = 0, j = 0, index = 0;

        while (i < m && j < n) {
            if (nums1[i] <= nums2[j]) {
                tmp[index++] = nums1[i++];
            } else {
                tmp[index++] = nums2[j++];
            }
        }

        for (; i < m; i++) {
            tmp[index++] = nums1[i];
        }

        for (; j < n; j++) {
            tmp[index++] = nums2[j];
        }

        for (int k = 0; k < m + n; k++) {
            nums1[k] = tmp[k];
        }
    }
}

优化

不创建临时数组，而是直接在 nums1中进行，但是因为 nums1中前半段存储了数据，所以需要倒着存，即把大的数先存到 nusm1的末尾

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        // i, j表示下标
        int i = m - 1, j = n - 1;
        int len = nums1.length - 1;

        // 注意外层循环的条件是用 j 判定的，而不是 len
        while (j >= 0) {
            if (i >= 0 && nums1[i] >= nums2[j]) {
                nums1[len--] = nums1[i--];
            } else {
                nums1[len--] = nums2[j--];
            }
        }
    }
}

[94] 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的中序遍历。

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

输入：root = [1,null,2,3]
输出：[1,3,2]

输入：root = []
输出：[]

输入：root = [1]
输出：[1]

输入：root = [1,2]
输出：[2,1]

输入：root = [1,null,2]
输出：[1,2]

解法一：

中序遍历，针对每个节点进行递归的处理

class Solution {
    // 创建一个全局的 list
    List<Integer> list = new ArrayList<>();
    
    public List<Integer> inorderTraversal(TreeNode root) {
        // 递归退出条件
        if (root == null) {
            return list;
        }
        
        // 中序遍历
        inorderTraversal(root.left);
        list.add(root.val);
        inorderTraversal(root.right);
        // 每次都返回全局的 list
        return list;
    }
}



/**
*  同样是递归，这样写可能会更好一些
*/
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();

        inorder(root, list);
        return list;
    }

    // 额外设置一个函数，实现递归
    private void inorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        inorder(root.left, list);
        list.add(root.val);
        inorder(root.right, list);
    }
}

❤ 解法二：

借用栈实现迭代遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        // 构建用于临时存储 TreeNode的栈
        Deque<TreeNode> deque = new LinkedList<>();

        /*
        	开始向左遍历树，先将途经的所有 TreeNode都添加到栈中
        	直到遇见 null以后再从 栈中获取元素，依据栈后进先出的特性，可以获取到最后一次迭代的元素，它就是第一个加入到结果 list中的元素
        	然后向右移动一格，再继续上述步骤
        */
        while (root != null || !deque.isEmpty()) {
            while (root != null) {
                deque.push(root);
                root = root.left;
            }
            root = deque.pop();
            list.add(root.val);
            root = root.right;
        }
        return list;
    }
}

❤ 解法三：

Morris中序遍历

这是另一种非递归遍历二叉树的方法，可以将空间复杂度降低为 O(1)

类似建立一个中序排序树的样子…

具体步骤：

如果节点 P无左孩子，那么就先访问 P，然后访问 P的右孩子（即 P = P.right）
如果节点 P有左孩子，那么就找到其左子树上最右的节点（即左子树中序遍历的最后一个结点，亦即节点 P在中序遍历时的前驱节点），将其命名为 preDecessor
- 如果 preDecessor的右孩子为空，则将其右孩子指向 P，然后访问 P的左孩子（即 P = P.left），并且打断 P到其左孩子的链接
重复以上步骤，直至访问完整棵树

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        TreeNode preDecessor = null;

       while (root != null) {
            //如果左节点不为空，就将当前节点连带右子树全部挂到左节点的最右子树下面
            if (root.left != null) {
                // 定位到左孩子的最右节点
                preDecessor = root.left;
                while (preDecessor.right != null) {
                    preDecessor = preDecessor.right;
                }
                
                // 将其 right指向 root
                preDecessor.right = root;
                
                //将 root指向 root的 left，并且打断 root和 root.left的链接
                TreeNode tmp = root;
                root = root.left;
                tmp.left = null;
            } else {
                 //左子树为空，则打印这个节点，并向右边遍历
                list.add(root.val);
                root = root.right;
            }
        }
        return list;
    }
}

[98] 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：
输入：root = [2,1,3]
输出：true
示例 2：
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。
提示：

树中节点数目范围在[1, 104] 内

-231 <= Node.val <= 231 - 1

Related Topics

树

深度优先搜索

二叉搜索树

二叉树

解法一：

递归

详见 day12: 二叉搜索树基础

class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, null, null);
    }

    private boolean isValidBST(TreeNode root, Integer min, Integer max) {

        if (root == null) {
            return true;
        }

        if (min != null && root.val <= min) {
            return false;
        }

        if (max != null && root.val >= max) {
            return false;
        }

        return isValidBST(root.left, min, root.val) && isValidBST(root.right, root.val, max);
    }
}

解法二：

中序遍历

因为 BST的中序遍历结果是一个递增的数组，所以可以通过对其的中序遍历的结果来判断其值

class Solution {
    // 定义上一个遍历到的值
    long prev = Long.MIN_VALUE;

    public boolean isValidBST(TreeNode root) {
        return traverse(root);
    }

    private boolean traverse(TreeNode root) {
        // base condition
        if (root == null) {
            return true;
        }

        // 中序遍历
        if (!traverse(root.left)) {
            return false;
        }

		// 判断上一个节点的值和当前节点的值的关系
        if (prev >= root.val) {
            return false;
        }
        // 更新上一个节点的值
        prev = root.val;
        return traverse(root.right);
    }
}

[100] 相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

输入：p = [1,2,3], q = [1,2,3]
输出：true

输入：p = [1,2], q = [1,null,2]
输出：false

输入：p = [1,2,1], q = [1,1,2]
输出：false

解法一：

递归遍历每个节点

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        // 如果两个节点都是 null的话，就正常
        if (p == null && q == null) {
            return true;
            // 在两个节点都不是 null的条件下，判断它们的值
        } else if (p != null && q != null) {
            // 判断值，并且递归调用
            return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
        }
        // 其他条件下，一定是结构不符合
        return false;
    }
}

[101] 对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ \ /
3 4 4 3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/
2 2
\
3 3

进阶：
你可以运用递归和迭代两种方法解决这个问题吗？

解法一：

通过递归判断

先将左子树的所有左右节点反转，然后判断

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }

        // 将左子树的左右节点反转反转
        if (root.left == null) {
            if (root.right != null)
                return false;
            else return true;
        } else {
            switchNode(root.left);
        }

        // 判断左右子树是否相同
        return judgeNode(root.left, root.right);
    }

    // 实际反转函数
    private void switchNode(TreeNode root) {
        if (root == null)
            return;

        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        switchNode (root.left);
        switchNode (root.right);
    }

    // 实际判断函数
    private boolean judgeNode(TreeNode r1, TreeNode r2) {
        if (r1 == null && r2 == null) {
            return true;
        } else if (r1 == null || r2 == null) {
            return false;
        }
        return r1.val == r2.val && judgeNode(r1.left, r2.left) && judgeNode(r1.right, r2.right);
    }
}

解法二：

直接就通过递归判断

r1.left == r2.right && r1.right == r2.left

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }

        return judgeNode(root.left, root.right);
    }

    private boolean judgeNode(TreeNode r1, TreeNode r2) {
        if (r1 == null && r2 == null) {
            return true;
        } else if (r1 == null || r2 == null) {
            return false;
        } else {
            return r1.val == r2.val && judgeNode(r1.left, r2.right) && judgeNode(r1.right, r2.left);
        }
    }
}

解法三：

迭代

[104] 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，
 3
/ \\
9  20
 /  \\
15   7
返回它的最大深度 3 。

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

解法一：

后根递归

class Solution {
    public int maxDepth(TreeNode root) {
        // 退出递归的条件
        if (root == null) {
            return 0;
        }

        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

❤ 解法二：

回溯

class Solution {
    int res = 0;
    int depth = 0;

    public int maxDepth(TreeNode root) {
        // base condition
        // 只当遍历到叶子节点，才更新 res
        if (root == null) {
            res = Math.max(res, depth);
            return res;
        }

        depth++;
        maxDepth(root.left);
        maxDepth(root.right);
        depth--;

        return res;
    }
}

[108] 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
示例 2：
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示：

1 <= nums.length <= 104

-104 <= nums[i] <= 104

nums 按 严格递增 顺序排列

Related Topics

树

二叉搜索树

数组

分治

二叉树

解法一：

递归

因为数组本身就是有序的，所以可以通过二分查找，直接创建二叉搜索树

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        if (nums.length == 0) {
            return null;
        }

        return sortedArrayToBST(nums, 0, nums.length - 1);
    }

    private TreeNode sortedArrayToBST(int[] nums, int start, int end) {
        if (start > end) {
            return null;
        }

        // 中间数就是根节点
        int mid = (start + end) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        // 左右节点
        root.left = sortedArrayToBST(nums, start, mid - 1);
        root.right = sortedArrayToBST(nums, mid + 1, end);

        return root;
    }
}

[111] 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：2
示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
提示：

树中节点数的范围在 [0, 105] 内

-1000 <= Node.val <= 1000

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

解法一：

递归，也可以看作是 DFS

递归遍历节点，每次返回左右子树中小的那个值

此时会递归整棵树的所有节点，最后再返回值

class Solution {
    public int minDepth(TreeNode root) {
        // 如果 root是 null，就返回 0
        if (root == null) {
            return 0;
            // 如果 root是叶子节点，就返回 1
        } else if (root.left == null && root.right == null) {
            return 1;
			// 如果 root是单支的，就像另一侧递归，并且加上当前节点 ( +1)
        } else if (root.left == null) {
            return minDepth(root.right) + 1;
        } else if (root.right == null) {
            return minDepth(root.left) + 1;
        }

        // 如果 root两侧都有节点，那么就递归左右侧，返回小的那个，并且加上当前节点 ( + 1)
        return Math.min(minDepth(root.left) + 1, minDepth(root.right) + 1);
    }
}

解法二：

BFS

广度遍历，从 root节点开始扩散，一旦找到叶子节点就返回

详见 day13: BFS 搜索算法

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        // 定义一个队列用作临时节点的存储，存的是某一层的节点
        Queue<TreeNode> queue = new LinkedList<>();
        // 先把 root进队
        queue.offer(root);
        // 记录二叉树的高度
        int depth = 1;

        while (!queue.isEmpty()) {
            // size即是当前层中节点的数量
            int size = queue.size();

            // 遍历当前层，并且加入下一层的节点
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                // 如果这个节点是叶子节点，那么直接返回
                if (cur.left == null && cur.right == null) {
                    return depth;
                }
                // 否则将它的左右非空孩子节点入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            
            // 当前层遍历结束，depth++
            depth++;
        }

        return depth;
    }
}

[114] 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]
示例 2：
输入：root = []
输出：[]
示例 3：
输入：root = [0]
输出：[0]
提示：

树中结点数在范围 [0, 2000] 内

-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

Related Topics

栈

树

深度优先搜索

链表

二叉树

解法一：

后序遍历

具体解法看 day11: 二叉树训练

class Solution {
    public void flatten(TreeNode root) {

        // 递归退出条件
        if (root == null) {
            return;
        }

        // 后序遍历
        flatten(root.left);
        flatten(root.right);

        // 获取当前节点的左右子节点
        TreeNode leftNode = root.left;
        TreeNode rightNode = root.right;

        // 设置左子节点成为右子节点
        root.right = leftNode;
        // 设置左子节点为空
        root.left = null;

        // 定位到当前节点的最右侧
        while (root.right != null) {
            root = root.right;
        }
        // 接上原来的右子节点
        root.right = rightNode;
    }
}

[118] 杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:

1 <= numRows <= 30

Related Topics

数组

动态规划

解法一：

构造内外集合

如果是第一个内集合，直接存入 1，然后将内集合存入外集合
如果不是，那么获取上一个内集合，遍历上一个内集合，计算值，添加到当前内集合，然后将当前内集合存入外集合

返回外集合

class Solution {
    public List<List<Integer>> generate(int numRows) {

        List<List<Integer>> out = new ArrayList<>();

        for (int i = 1; i <= numRows; i++) {
            List<Integer> in = new ArrayList<Integer>();

            // base condition
            if (i == 1) {
                in.add(1);
            } else {
                // i >= 2
                List<Integer> prev = out.get(i - 2);
                for (int j = 0; j < i; j++) {
                    if (j == 0 || j == i - 1) {
                        in.add(1);
                    } else {
                        in.add(prev.get(j - 1) + prev.get(j));
                    }
                }
            }
            out.add(in);
        }

        return out;
    }
}

[121] 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
  注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 105
0 <= prices[i] <= 104

Related Topics

数组

动态规划

解法一：

维护 最小元素 s 和 最大差值 l

遍历 int[] price数组，每到一个位置，就将当前元素和 s进行比较，保留或更新最小元素；同时计算差值

注意：不要只记录数组中的最大值，而要记录 最大差值。

class Solution {
    public int maxProfit(int[] prices) {        
        // 这里的max指能赚的最多的钱，min指到 i为止最低的股价
        int max = 0, min = price[0];
        for (int i = 1; i < price.length; i++) {
            min = Math.min(min, price[i]);
            max = Math.max(max, prive[i] - min);
        }
        return max;
    }
}

如果想思考得清晰些的话，也可以再引入 int[] dp数组

dp[i]表示截至 price[i]，遇到的最小的元素

但是因为我们不需要在 int[] dp构造之后再操作数组了，所以其实是没有必要的

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        // 记录到 i为止的收益
        int[] dp = new int[len];
        // 当前遇到的最小值
        int min = prices[0];
        // 当前遇到的最大值
        int max = 0;
        dp[0] = 0;

        for (int i = 1; i < len; i++) {
            min = Math.min(min, prices[i]);
            dp[i] = prices[i] - min;
            max = Math.max(dp[i], max);
        }

        return max;
    }
}

[125] 验证回文串

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明：本题中，我们将空字符串定义为有效的回文串。

示例 1:
输入: "A man, a plan, a canal: Panama"
输出: true
解释："amanaplanacanalpanama" 是回文串
示例 2:
输入: "race a car"
输出: false
解释："raceacar" 不是回文串
提示：

1 <= s.length <= 2 * 105

字符串 s 由 ASCII 字符组成

Related Topics

双指针

字符串

解法一：

字符串转为小写字符数组，进行首位元素比较，出现不同就返回 false

class Solution {
    public boolean isPalindrome(String s) {
		// 空字符串返回 true
        if (s == null || s.isEmpty()) {
            return true;
        }

        // 获取小写字符数组
        s = s.toLowerCase();
        char[] arr = s.toCharArray();
        int i = 0, j = s.length() - 1;

        // 双指针遍历数组
        while (i < j) {
            char ci = arr[i];
            char cj = arr[j];
            // 判断是否是正常的字母或数字
            if (!Character.isLetterOrDigit(ci)) {
                i++;
                continue;
            }

            if (!Character.isLetterOrDigit(cj)) {
                j--;
                continue;
            }

            if (ci != cj) {
                return false;
            }

            i++;
            j--;
        }

        return true;
    }
}

解法二：

正则匹配

先替换其他的字符，再将原字符串反转后比较

class Solution {
    public boolean isPalindrome(String s) {
        String s1 = s.replaceAll("[^A-Za-z0-9]", "").toLowerCase();
        String s2 = new StringBuffer(s1).reverse().toString();
        return s1.equals(s2);
    }
}

♥ [136] 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
Related Topics

位运算

数组

解法一：

排序

class Solution {
    public int singleNumber(int[] nums) {
        Arrays.sort(nums);
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] == nums[i - 1]) {
                i++;
                continue;
            }

            return nums[i - 1];
        }

        return nums[nums.length - 1];
    }
}

♥ 解法二：

位运算

任何数异或自己等于 0 a ^ a = 0

任何数异或 0 等于自己 a ^ 0 = a

class Solution {
    public int singleNumber(int[] nums) {
        int res = 0;
        for (int num : nums) {
            res ^= num;
        }
        return res;
    }
}

[141] 环形链表

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
提示：

链表中节点的数目范围是 [0, 104]

-105 <= Node.val <= 105

pos 为 -1 或者链表中的一个 有效索引 。

Related Topics

哈希表

链表

双指针

解法一：

每次遍历一个结点，就放到 HashSet中，然后加入前判断节点是否有重复。

public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) {
            return false;
        }
        
        Set<ListNode> set = new HashSet<>();
        while(head != null) {
            if (!set.add(head)) {
                return true;
            }
            head = head.next;
        }
        return false;
    }
}

解法二：

快慢指针，当慢指针超越快指针时，就说明有环；否则无环

public class Solution {
    public boolean hasCycle(ListNode head) {
        // 声明快慢指针
        ListNode fast = head, slow = head;
        
        // 快慢指针开始跑，只要成环，就一定会相遇
        while(fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                return true;
            }
        }

        // 没有相遇
        return false;
    }
}

[144] 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：
输入：root = [1,null,2,3]
输出：[1,2,3]
示例 2：
输入：root = []
输出：[]
示例 3：
输入：root = [1]
输出：[1]
示例 4：
输入：root = [1,2]
输出：[1,2]
示例 5：
输入：root = [1,null,2]
输出：[1,2]
提示：

树中节点数目在范围 [0, 100] 内

-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

Related Topics

栈

树

深度优先搜索

二叉树

解法一：

递归

创建全局变量集合，存储数据；

使用额外的自定义函数，递归遍历树，将值添加到集合中

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        traverse(root);
        return res;
    }

    private void traverse(TreeNode root) {
        // base condition
        if (root==null) {
            return;
        }
        
        // 先序
        res.add(root.val);
        traverse(root.left);
        traverse(root.right);
    }
}

不使用全局变量集合，每次递归创建一个集合，使用 addAll()将左右子树的遍历结果添加到当前根节点中

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        // 对每个节点的遍历都创建一次集合
        List<Integer> res = new ArrayList<>();
        // base condition
        if (root == null) {
            return res;
        }

        // 添加当前节点的值
        res.add(root.val);
        // 添加左右子树遍历后的值
        res.addAll(preorderTraversal(root.left));
        res.addAll(preorderTraversal(root.right));

        return res;
    }
}

解法二：

迭代

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        // 使用栈来先序遍历二叉树
        Stack<TreeNode> stack = new Stack<>();
        TreeNode p = root;

        while(!stack.isEmpty() || p != null) {
            // 直接处理 p
            while(p != null) {
                res.add(p.val);
                stack.push(p);
                p = p.left;
            }
            p = stack.pop();
            p = p.right;
        }

        return res;
    }
}

中序迭代的代码

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        // 使用栈来先序遍历二叉树
        Stack<TreeNode> stack = new Stack<>();
        TreeNode p = root;

        while(!stack.isEmpty() || p != null) {
            // 直接处理 p
            while(p != null) {
                stack.push(p);
                p = p.left;
            }
            p = stack.pop();
            // 把操作拿到下面来
            res.add(p.val);
            p = p.right;
        }

        return res;
    }
}

[145] 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：
输入：root = [1,null,2,3]
输出：[3,2,1]
示例 2：
输入：root = []
输出：[]
示例 3：
输入：root = [1]
输出：[1]
提示：

树中节点的数目在范围 [0, 100] 内

-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

Related Topics

栈

树

深度优先搜索

二叉树

解法一：

递归

class Solution {
    List<Integer> res = new ArrayList<>();

    public List<Integer> postorderTraversal(TreeNode root) {
        traverse(root);
        return res;
    }

    private void traverse(TreeNode root) {
        if (root == null) {
            return;
        }

        traverse(root.left);
        traverse(root.right);
        res.add(root.val);
    }
}

[155] 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

示例:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

pop、top 和 getMin 操作总是在 非空栈 上调用。

Related Topics

栈

设计

解法一：

额外定义一个整形变量存储最小值，当有元素入栈时，更新最小值；当有元素出栈时，如果出栈的就是最小值，也要进行更新

class MinStack {

    Stack<Integer> stack;
    int min = Integer.MAX_VALUE;

    public MinStack() {
        stack = new Stack<>();
    }

    public void push(int val) {
        stack.push(val);
        min = Math.min(min, val);
    }

    public void pop() {
        Integer pop = stack.pop();
        if (min == pop) {
            min = Integer.MAX_VALUE;
            for (Integer integer : stack) {
                min = Math.min(min, integer);
            }
        }
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return min;
    }
}

解法二：

自定义一个结点类，类中包含了 curVal和 minVal

如果压栈时栈为空，curVal=minVal=val;

如果压栈时栈不空，curVal=val, minVal=getMin()

getMin()的实现为 return head.minVal;

重点在于，如果 min很早就入栈了，那么它不容易出栈，因此多次出栈操作后，min依旧是 min

但是如果 min最后才入栈，那么之前的节点中 minVal存储的都不是 min，而是它入栈时的那个 min，当该节点出栈时，最小的 min一定已经出栈，那么此时的 min一定就是节点中记录的 minVal，因此不需要在 pop()函数处进行特殊的处理

[160] 相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

listA 中节点数目为 m
listB 中节点数目为 n
0 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA + 1] == listB[skipB + 1]

进阶：你能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案？

Related Topics

哈希表

链表

双指针

解法一：

通过 HashSet添加 ListNode后返回的 boolean值判断是否为 false，表示是否有重复

	public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        
        if (headA == null || headB == null) {
            return null;
        }

        HashSet<ListNode> set = new HashSet<ListNode>();
        while (headA != null) {
            set.add(headA);
            headA = headA.next;
        }

        while (headB != null) {
            if (!set.add(headB)) {
                return headB;
            }
            headB = headB.next;
        }
        return null;

    }
}

解法二：

双指针

设置指针 pA和 pB，当一个指针走到 null时，将其设置为另一个链表的首元结点，继续走，直到 pA遇到了 pB

如果两个链表存在相交的位置，就一定会遇到，每个指针只要走完两个链表各自独立的节点和一段公共的点就行了

如果两个链表没有相交的位置，也会在 null的时候同时遇到：lengthA * lengthB == lengthB * lengthA

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        // 分别指向两个链表的首元节点
        ListNode p = headA, q = headB;
        // 这里不需要考虑两个链表没有交点的情况，因为即使没有交点，一轮遍历下来，最终二者都会变为 null，p==q，会跳出循环，然后返回 p = null;
        while(p != q) {
            p = p == null ? headB : p.next;
            q = q == null ? headA : q.next;
        }

        return p;
    }
}

[169] 多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：
输入：nums = [3,2,3]
输出：3
示例 2：
输入：nums = [2,2,1,1,1,2,2]
输出：2
提示：

n == nums.length

1 <= n <= 5 * 104

-109 <= nums[i] <= 109

进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

Related Topics

数组

哈希表

分治

计数

排序

解法一：

统计数组中的最小值出现频率，每次统计之后修改最小值为 Integer.MAX_VALUE

class Solution {
    public int majorityElement(int[] nums) {
        int cnt = 0;
        int min = 0;
        while(cnt <= nums.length / 2) {
            // min = Arrays.stream(nums).min().getAsInt();
            min = findMin(nums); 
            cnt = countMin(nums, min);
        }
        return min;
    }

    private int findMin(int[] nums) {
        int min = Integer.MAX_VALUE;
        for(int x : nums) {
            min = Math.min(min, x);
        }
        return min;
    }

    private int countMin(int[] nums, int t) {
        int cnt = 0;
        for(int i = 0; i < nums.length; i++) {
            if (nums[i] == t) {
                cnt++;
                nums[i] = Integer.MAX_VALUE;
            }
        }

        return cnt;
    }
}

解法二：

投票法

因为要求的那个多数元素出现的次数最多，也就是说到最后，cnt 一定 > 0；

而 cnt是与 candidate同步的，那么 candidate最后一定会是那个多数元素

class Solution {
    public int majorityElement(int[] nums) {
        
        int cnt = 0;
        int candidate = 0;
        for(int x : nums) {
            // cnt为 0 时更换 candidate
            if (cnt == 0) {
                candidate = x;
            }
			// 投票
            if (candidate == x) {
                cnt++;
            } else {
                cnt--;
            }
        }

        return candidate;
    }
}

[190] 颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在 示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。

示例 1：

输入：n = 00000010100101000001111010011100
输出：964176192 (00111001011110000010100101000000)
解释：输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
  因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

示例 2：

输入：n = 11111111111111111111111111111101
输出：3221225471 (10111111111111111111111111111111)
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
  因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

提示：

输入是一个长度为 32 的二进制字符串

进阶: 如果多次调用这个函数，你将如何优化你的算法？

Related Topics

位运算

分治

解法一：

位运算

定义返回的值为 res

每次 res左移一位
然后 res加上 n中最右侧的值
随后 n右移一位，移除被加的那一位

如此反复 32次，直到移除原来 res中的所有 0

注意：针对二进制的计算，不能用字符串来操作，尽可能的用位运算解决

public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        int res = 0;
        // 反复 32次
        for (int i = 0; i < 32; i++) {
            // res右移
            res <<= 1;
            // 获取 n的最后一位的值，加到 res上
            res += n & 1;
            // n左移
            n >>= 1;
        }

        return res;
    }
}

[191] 位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 '1' 的个数（也被称为汉明重量）。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

示例 1：

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例 2：

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例 3：

输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

提示：

输入必须是长度为 32 的 二进制串 。

进阶：

如果多次调用这个函数，你将如何优化你的算法？

Related Topics

位运算

解法一：

位运算

每次右移一位，让最后一位同 1做 &操作，如果是 true，则表示该位是 1

注意：不能直接把输入转化为字符串然后遍历

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        for (int i = 0; i < 32; i++) {
            if ((n >>> i & 1) == 1) {
                count++;
            }
        }

        return count;
    }
}

[203] 移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回新的头节点。

示例 1：
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：
输入：head = [], val = 1
输出：[]

示例 3：
输入：head = [7,7,7,7], val = 7
输出：[]

解法一：

迭代

就遍历整个链表，如果值相等就移除。

注意添加头结点，保证首元结点可以和其他节点一样简单的移除，不需要其他的判断。

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        if (head == null) {
            return head;
        }

        // 添加首元结点
        ListNode dummy = new ListNode();
        dummy.next = head;

        // 因为是单链表，所以需要两个指针
        ListNode prev = dummy, cur = head;
        while (cur != null) {
            // 如果值相等，就移除，之后 prev不动，cur重新设置为 prev.next
            if (cur.val == val) {
                prev.next = cur.next;
                cur.next = null;
                cur = prev.next;
            } else {
                // 值不相等，那么就一起后移一位
                prev = prev.next;
                cur = cur.next;
            }
        }
        // 返回首元结点
        return dummy.next;
    }
}

解法二：

递归

设置递归结束条件：head == null
如果 head.val == val，那么就移除 head，返回 head.next

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        if (head == null) {
            return head;
        }

        head.next = removeElements(head.next, val);
        /*
            假设现在链表中只剩下了 head节点
                head.next == null
                head.val == val
            此时 head本身需要被移除，那么就返回 head.next

            ---

            假设现在链表中剩下 2个节点，head和 tail
                head.next == tail
                tail.next == null
                tail.val != val
                head.val == val
            此时 head需要被移除，就把 head之后的一个结点返回
         */
        return head.val == val ? head.next : head;
    }
}

更好理解一点：

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        if (head == null) {
            return null;
        }

        if (head.val == val) {
            return removeElements(head.next, val);
        }

        head.next = removeElements(head.next, val);
        return head;
    }
}

♥ [204] 计数质数

统计所有小于非负整数 n 的质数的数量。

示例 1：
输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2：
输入：n = 0
输出：0
示例 3：
输入：n = 1
输出：0
提示：

0 <= n <= 5 * 106

Related Topics

数组

数学

枚举

数论

❤ 解法一：

埃氏筛

枚举 < 埃氏筛 < 欧式筛（线性筛） < 奇数筛

class Solution {
    public int countPrimes(int n) {
        boolean[] arr = new boolean[n];
        int cnt = 0;

        for (int i = 2; i < n; i++) {
            // 如果是 true就表示不是素数
            if (arr[i]) {
                continue;
            }

            cnt++;
            // 因为当前数字是素数，则它的所有倍数都不是素数
            for (int j = i; j < n; j += i) {
                arr[j] = true;
            }
        }

        return cnt;
    }
}

[206] 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
示例 2：
输入：head = [1,2]
输出：[2,1]
示例 3：
输入：head = []
输出：[]
提示：

链表中节点的数目范围是 [0, 5000]

-5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

Related Topics

递归

链表

解法一：

递归

因为要求链表反转，即屁股指向头，所以要先找到屁股

即先进行递归，在进行操作

每次递归结束后，返回操作之后的链表的头结点（即原来的链表的尾节点）

class Solution {
    public ListNode reverseList(ListNode head) {

        if (head == null) {
            return head;
        }
        
        return traverse(head);
    }

    private ListNode traverse(ListNode head) {
        if (head.next == null) {
            return head;
        }

        ListNode tail =  traverse(head.next);
		// 可以直接幻想，通过 traverse方法之后得到的链表的样子 -> 后半部分已经完成了逆序，前半部分还是正序，当前 head就是那个临界的位置
        head.next.next = head;
        head.next = null;

        return tail;

    }
}

解法二：

迭代
迭代链表中的每一个元素

class Solution {
    public ListNode reverseList(ListNode head) {
        
        if (head == null || head.next == null) {
            return head;
        }

        ListNode slow = head, fast = head.next;
        // 注意将首元节点的 next指针置为 null，否则会在头部成环
        head.next = null;
        ListNode tmp = null;

        // 遍历链表
        while (fast != null) {
            tmp = fast.next;
            fast.next = slow;
            slow = fast;
            fast = tmp;
        }

        return slow; 
    }
}

[217] 存在重复元素

给定一个整数数组，判断是否存在重复元素。

如果存在一值在数组中出现至少两次，函数返回 true 。如果数组中每个元素都不相同，则返回 false 。

示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
Related Topics

数组

哈希表

排序

解法一：

HashSet

class Solution {
    public boolean containsDuplicate(int[] nums) {
        HashSet<Integer> set = new HashSet<>();
        for (int num : nums) {
            if (!set.add(num)) {
                return true;
            }
        }

        return false;
    }
}

解法二：

排序

class Solution {
    public boolean containsDuplicate(int[] nums) {
        if (nums.length <= 1) {
            return false;
        }
        // 排序
        Arrays.sort(nums);
        // 找相邻重复元素
        for (int i = 0; i < nums.length - 1; i++) {
            if (nums[i] == nums[i + 1])
                return true;
        }
        return false;
    }
}

解法三：

流

class Solution {
    public boolean containsDuplicate(int[] nums) {
        return Arrays.stream(nums).distinct().count() != nums.length;
    }
}

[219] 存在重复元素Ⅱ

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：
输入：nums = [1,2,3,1], k = 3
输出：true
示例 2：
输入：nums = [1,0,1,1], k = 1
输出：true
示例 3：
输入：nums = [1,2,3,1,2,3], k = 2
输出：false
提示：

1 <= nums.length <= 105

-109 <= nums[i] <= 109

0 <= k <= 105

Related Topics

数组

哈希表

滑动窗口

解法一：

滑动窗口

class Solution {
    public boolean containsNearbyDuplicate(int[] nums, int k) {
        HashSet<Integer> window = new HashSet<>();

        int left = 0, right = 0;
        // 刚开始就只管往窗口里塞，塞到比 k大了在从窗口里减
        while(right < nums.length) {
            int in = nums[right++];
            if (!window.add(in)) {
                return true;
            }

            if (right > k) {
                int out = nums[left++];
                window.remove(out);
            }

        }

        return false;
    }
}

[225]用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：
输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
提示：

1 <= x <= 9

最多调用100 次 push、pop、top 和 empty

每次调用 pop 和 top 都保证栈不为空

进阶：你能否实现每种操作的均摊时间复杂度为 O(1) 的栈？换句话说，执行 n 个操作的总时间复杂度 O(n) ，尽管其中某个操作可能需要比其他操作更长的时间。你可以使用两个以上的队列。

Related Topics

栈

设计

队列

解法一：

使用队列模拟栈，出栈的时候，把队列前面的元素先移出来，除了栈顶元素都扔到队尾

另外，为了方便 top()方法的使用，需要额外增加一位记录队尾的元素

class MyStack {

    private Queue<Integer> queue;
    int top_elem;

    public MyStack() {
        queue = new LinkedList<>();
    }

    public void push(int x) {
        queue.offer(x);
        top_elem = x;
    }

    public int pop() {
        int size = queue.size();
        while (size > 2) {
            queue.offer(queue.poll());
            size--;
        }
        top_elem = queue.peek();
        queue.offer(queue.poll());
        return queue.poll();
    }

    public int top() {
        return top_elem;
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

[226] 翻转二叉树

翻转一棵二叉树。

示例：

输入：
  4
/   \\
2     7
/ \\   / \\
1   3 6   9
输出：
  4
/   \\
7     2
/ \\   / \\
9   6 3   1
备注:
这个问题是受到 Max Howell 的原问题启发的：

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

解法一：

递归遍历二叉树，使用先序遍历

class Solution {
    public TreeNode invertTree(TreeNode root) {

        if (root == null) {
            return null;
        }

        // 先处理
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        // 再递归
        invertTree(root.left);
        invertTree(root.right);

        return root;

    }
}

也可以进行后序操作：

class Solution {
    public TreeNode invertTree(TreeNode root) {

        if (root == null) {
            return null;
        }


        invertTree(root.left);
        invertTree(root.right);

        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;

        return root;

    }
}

更雅观一些

class Solution {
    public TreeNode invertTree(TreeNode root) {
        return reverse(root);
    }

    private TreeNode reverse(TreeNode root) {
        if (root == null) {
            return null;
        }

        TreeNode lNode = reverse(root.left);
        TreeNode rNode = reverse(root.right);

        root.left = rNode;
        root.right = lNode;

        return root;
    }
}

[232] 用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

进阶：

你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

示例：
输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false
提示：

1 <= x <= 9

最多调用 100 次 push、pop、peek 和 empty

假设所有操作都是有效的（例如，一个空的队列不会调用 pop 或者 peek 操作）

Related Topics

栈

设计

队列

解法一：

声明两个栈，每次元素入队列时先入栈1，出队列时从栈2出栈，如果栈2为空，就先把元素从栈1移动到栈2

class MyQueue {

    private Stack<Integer> s1;
    private Stack<Integer> s2;

    public MyQueue() {
        s1 = new Stack();
        s2 = new Stack();
    }

    public void push(int x) {
        s2.push(x);
    }

    public int pop() {
        if (s1.isEmpty()) {
            transfer(s1, s2);
        }
        return s1.pop();
    }

    public int peek() {
        if (s1.isEmpty()) {
            transfer(s1, s2);
        }
        return s1.peek();
    }

    public boolean empty() {
        return s1.isEmpty() && s2.isEmpty();
    }

    private void transfer(Stack<Integer> s1, Stack<Integer> s2) {
        while (!s2.isEmpty()) {
            s1.push(s2.pop());
        }
    }
}

[234] 回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例 1：
输入：head = [1,2,2,1]
输出：true
示例 2：
输入：head = [1,2]
输出：false
提示：

链表中节点数目在范围[1, 105] 内

0 <= Node.val <= 9

进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

Related Topics

栈

递归

链表

双指针

解法一：

快慢指针定位到链表的中点，反转后半段链表，然后分别从头尾向中间遍历

class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null) {
            return false;
        }

        ListNode fast = head, slow = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        // 获取链表中点
        ListNode mid = slow;
		// 反转后半段链表
        ListNode tail = reverse(mid);
        
        // 头尾向中间遍历
        while (tail != head && head != mid) {
            if (tail.val != head.val) {
                return false;
            }
            tail = tail.next;
            head = head.next;
        }

        return true;
    }


    private ListNode reverse(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        ListNode last = reverse(head.next);
        head.next.next = head;
        head.next = null;

        return last;
    }
}

[235] 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:

所有节点的值都是唯一的。

p、q 为不同节点且均存在于给定的二叉搜索树中。

Related Topics

树

深度优先搜索

二叉搜索树

二叉树

解法一：

充分利用二叉搜索树左小右大的特点，只要 p<root<q，就说明公共祖先就是 root

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       if (p.val > q.val) {
           return find(root, q, p);
       }

       return find(root, p, q);
    }

    private TreeNode find(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }

        if (root.val > q.val) {
            return find(root.left, p, q);
        } else if (root.val < p.val) {
            return find(root.right, p, q);
        }

        return root;
    }
}

[242] 有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。

示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
提示:

1 <= s.length, t.length <= 5 * 104

s 和 t 仅包含小写字母

进阶: 如果输入字符串包含 unicode 字符怎么办？你能否调整你的解法来应对这种情况？

Related Topics

哈希表

字符串

排序

解法一：

先遍历一个字符串，使用哈希表记录其中字符出现的次数；

再遍历另一个字符串，逐个字符减去一次次数；

最后判断值是否都是 0

class Solution {
    public boolean isAnagram(String s, String t) {

        HashMap<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);
        }

        for (int i = 0; i < t.length(); i++) {
            map.put(t.charAt(i), map.getOrDefault(t.charAt(i), 0) - 1);
        }

        for (Integer value : map.values()) {
            if (value != 0) {
                return false;
            }
        }

        return true;
    }
}

优化：

使用数组来代替哈希表 int[] letters = new int[26]，具体的定位为 letters[char-'a']

解法二：

先排序，再比较

class Solution {
    public boolean isAnagram(String s, String t) {
        char[] arrS = s.toCharArray();
        char[] arrT = t.toCharArray();

        Arrays.sort(arrS);
        Arrays.sort(arrT);

        return Arrays.equals(arrS, arrT);
    }
}

[268]丢失的数字

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。

示例 4：

输入：nums = [0]
输出：1
解释：n = 1，因为有 1 个数字，所以所有的数字都在范围 [0,1] 内。1 是丢失的数字，因为它没有出现在 nums 中。

提示：

n == nums.length
1 <= n <= 104
0 <= nums[i] <= n
nums 中的所有数字都 独一无二

进阶：你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?

Related Topics

位运算

数组

哈希表

数学

排序

解法一：

排序

先对数组排序，然后逐位比较元素，如果 nums[i] != i则返回 i，否则返回 nums.length

class Solution {
    public int missingNumber(int[] nums) {
        Arrays.sort(nums);
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != i) {
                return i;
            }
        }

        return nums.length;
    }
}

解法二：

位运算

对数组内的所有数和它的下标+1 一起做位运算，如果数存在，那么因为经过两次位运算，值仍为 0；如果数不存在，只经过一次位运算，剩下来的就是那个数

class Solution {
    public int missingNumber(int[] nums) {
        int ret = 0;
        for (int i = 0; i < nums.length; i++) {
            ret = ret ^ (i + 1) ^ nums[i];
        }

        return ret;
    }
}

相同的操作，可以采用数字的加减实现

把数组内的所有数相加，同时减去下标+1，剩下的就是缺的数

class Solution {
    public int missingNumber(int[] nums) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum = sum + i + 1 - nums[i];
        }
        return sum;
    }
}

[278] 第一个错误的版本

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例 1：

输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false 
调用 isBadVersion(5) -> true 
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。

示例 2：

输入：n = 1, bad = 1
输出：1

提示：

1 <= bad <= n <= 231 - 1

Related Topics

二分查找

交互

解法一：

二分查找

运用二分查找寻找边界，等于是找左边界

通过 isBadVersion(mid)判断是否找到，如果找到了，设置right=mid
如果没找到，说明出错的版本一定在右半边，设置 left = mid + 1

最后返回 left

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {

        int left = 0, right = n;

        while (left < right) {
            int mid = left + (right - left) / 2;

            if (isBadVersion(mid)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }

        return left;
    }
}

[283] 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:

必须在原数组上操作，不能拷贝额外的数组。

尽量减少操作次数。

Related Topics

数组

双指针

解法一：

双指针+拷贝

把非零元素通过拷贝堆到数组的左边，右边全部置零

class Solution {
    public void moveZeroes(int[] nums) {

        /*
        思路：
        1. 快慢指针遍历，如果不是 0，就把 fast内容赋值给 slow
        2. fast跑完之后，把 slow之后的内容全部置为 0
         */

        int fast = 0, slow = 0;

        while (fast < nums.length) {
            if (nums[fast] != 0) {
                nums[slow] = nums[fast];
                slow++;
            }
            fast++;
        }
        for (int i = slow; i < nums.length; i++) {
            nums[i] = 0;
        }

    }
}

第三次手写

class Solution {
    public void moveZeroes(int[] nums) {
        int idx = 0;
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] != 0) {
                nums[idx++] = nums[i];
            }
        }

        for(;idx<nums.length;idx++) {
            nums[idx] = 0;
        }
    }
}

[303] 区域和检索 - 数组不可变

给定一个整数数组 nums，求出数组从索引 i 到 j（i ≤ j）范围内元素的总和，包含 i、j 两点。

实现 NumArray 类：

NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 从索引 i 到 j（i ≤ j）范围内元素的总和，包含 i、j 两点（也就是 sum(nums[i], nums[i + 1], ... , nums[j])）

示例：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

提示：

0 <= nums.length <= 104
-105 <= nums[i] <= 105
0 <= i <= j < nums.length
最多调用 104 次 sumRange 方法

Related Topics

设计

数组

前缀和

解法一：

直接遍历从 left到 right的数据，然后相加求和并返回

但是此时时间复杂度为 O(N)

class NumArray {

    private int[] nums;

    public NumArray(int[] nums) {
        this.nums = nums;
    }
    
    public int sumRange(int left, int right) {
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }
}

解法二：

使用前缀和，在构造数组时，数组的每个元素存储的是当前 位置的值 + 前一个节点的值的和

因此，在进行范围计算的时候，只需要两个元素相减就行，此时的时间复杂度为 O(1)

class NumArray {

    private int[] preNums;

    public NumArray(int[] nums) {

        this.preNums = new int[nums.length + 1];

        for (int i = 1; i < preNums.length; i++) {
            preNums[i] = preNums[i - 1] + nums[i - 1];
        }
    }

    public int sumRange(int left, int right) {
        return preNums[right + 1] - preNums[left];
    }
}

[326] 3 的幂

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。

整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x

示例 1：
输入：n = 27
输出：true
示例 2：
输入：n = 0
输出：false
示例 3：
输入：n = 9
输出：true
示例 4：
输入：n = 45
输出：false
提示：

-231 <= n <= 231 - 1

进阶：你能不使用循环或者递归来完成本题吗？

Related Topics

递归

数学

解法一：

迭代

class Solution {
    public boolean isPowerOfThree(int n) {
        if (n > 1) {
            while (n % 3 == 0) {
                n /= 3;
            }
        }

        return n == 1;
    }
}

递归

class Solution {
    public boolean isPowerOfThree(int n) {
        if (n > 1 && n % 3 == 0) {
            return isPowerOfThree(n / 3);
        }

        return n == 1;
    }
}

进阶

使用 Java的 Math类方法，直接取 log3(n)

但是因为只有 log()和 log10()，所以使用换底公式

另外，因为 Integer范围内，最大的 3的幂为 1162261467，所以，可以直接让 1162261467 / n，如果结果为整数，就可以。

[338] 比特位计数

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：
输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10
示例 2：
输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
提示：

0 <= n <= 105

进阶：

很容易就能实现时间复杂度为 O(n log n) 的解决方案，你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗？

你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

Related Topics

位运算

动态规划

解法一：

硬做

class Solution {
    public int[] countBits(int n) {
        int[] res = new int[n + 1];
        for(int i = 0; i <= n; i++) {
            res[i] = cntVal(i);
        }
        return res;
    }

    private int cntVal(int x) {
        int cnt = 0;
        while(x != 0) {
            cnt += (x & 1);
            x = x >> 1;
        }
        return cnt;
    }
}

解法二：

利用 x & (x - 1)去除数字二进制后最右边的 1 的特性

也就是说 x中 1 的个数等于 x & (x - 1)中 1 的个数 + 1

class Solution {
    public int[] countBits(int n) {
        int[] res = new int[n + 1];
        for(int i = 1; i <= n; i++) {
            res[i] = res[i & (i - 1)] + 1;
        }
        return res;
    }
}

[344] 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

示例 1：
输入：s = ["h","e","l","l","o"]
输出：["o","l","l","e","h"]
示例 2：
输入：s = ["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]
提示：

1 <= s.length <= 105

s[i] 都是 ASCII 码表中的可打印字符

Related Topics

递归

双指针

字符串

解法一：

双指针一头一尾遍历数组，两端交换，直到指针相遇

class Solution {
    public void reverseString(char[] s) {
        if (s == null || s.length <= 1) {
            return;
        }

        int i = 0, j = s.length - 1;
        while (i < j) {
            char tmp = s[i];
            s[i] = s[j];
            s[j] = tmp;

            i++;
            j--;
        }
    }
}

[349] 两个数组的交集

给定两个数组，编写一个函数来计算它们的交集。

示例 1：
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]
示例 2：
输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
说明：

输出结果中的每个元素一定是唯一的。

我们可以不考虑输出结果的顺序。

Related Topics

数组

哈希表

双指针

二分查找

排序

解法一：

暴力解法，HashSet

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        HashSet<Integer> res = new HashSet<>();

        HashSet<Integer> tmp = new HashSet<>();
        for (int i : nums1) {
            tmp.add(i);
        }

        for (int i : nums2) {
            if (tmp.contains(i)) {
                res.add(i);
            }
        }

        int[] arr = new int[res.size()];
        int k = 0;
        for (int i : res) {
            arr[k++] = i;
        }

        return arr;
    }
}

解法二：

先对两个数组排序，然后同时遍历两个数组

如果值相等，就判断该值是否已被记录
如果值不等，就把值小的那个数组的索引 + 1

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
      
        Arrays.sort(nums1);
        Arrays.sort(nums2);

        int[] arr = new int[nums1.length + nums2.length];
        /*
        ia: arr中的索引
        i1：nums1 中的索引
        i2：nums2 中的索引
        */
        int ia = 0, i1 = 0, i2 = 0;
        // 同时遍历两个数组
        while (i1 < nums1.length && i2 < nums2.length) {
            int n1 = nums1[i1], n2 = nums2[i2];
            // 对值进行判断和记录
            if (n1 == n2) {
                if (ia == 0 || arr[ia - 1] != n1) {
                    arr[ia++] = n1;
                }
                i1++;
                i2++;
            } else if (n1 > n2) {
                i2++;
            } else if (n2 > n1) {
                i1++;
            }
        }

        // 返回一个大小正常的数组
        return Arrays.copyOfRange(arr, 0, ia);
    }
}

[350] 两个数组的交集Ⅱ

给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。

示例 1：
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]
示例 2:
输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]
提示：

1 <= nums1.length, nums2.length <= 1000

0 <= nums1[i], nums2[i] <= 1000

*进阶*：

如果给定的数组已经排好序呢？你将如何优化你的算法？

如果 nums1 的大小比 nums2 小，哪种方法更优？

如果 nums2 的元素存储在磁盘上，内存是有限的，并且你不能一次加载所有的元素到内存中，你该怎么办？

Related Topics

数组

哈希表

双指针

二分查找

排序

解法一：

排序后双指针

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        Arrays.sort(nums1);
        Arrays.sort(nums2);

        int[] arr = new int[nums1.length + nums2.length];
        int ia = 0, i1 = 0, i2 = 0;
        while (i1 < nums1.length && i2 < nums2.length) {
            int n1 = nums1[i1], n2 = nums2[i2];
            if (n1 == n2) {
                arr[ia++] = n1;
                i1++;
                i2++;
            } else if (n1 > n2) {
                i2++;
            } else {
                i1++;
            }
        }

        return Arrays.copyOfRange(arr, 0, ia);
    }
}

解法二：

哈希表

先对 nums1 和 nums2的长度进行判断，优先将短数组中的元素存入 map中

遍历长数组中的元素，判断其是否在 map中存在

若存在，则添加到结果数组中，并且将 map中保存的值减一，当值小于等于0时，移除该值

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {

        if (nums1.length > nums2.length) {
            return intersect(nums2, nums1);
        }

        // 先把一个集合存入 map中
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i : nums1) {
            map.put(i, map.getOrDefault(i, 0) + 1);
        }

        int[] arr = new int[nums1.length];
        int k = 0;
        for (int i : nums2) {
            Integer cnt = map.getOrDefault(i, 0);
            // 如果该数在交集中
            if (cnt > 0) {
                arr[k++] = i;
                cnt--;
                if (cnt > 0) {
                    map.put(i, cnt);
                } else {
                    map.remove(i);
                }
            }
        }

        return Arrays.copyOfRange(arr, 0, k);
    }
}

[367] 有效的完全平方数

给定一个 正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

进阶：不要 使用任何内置的库函数，如 sqrt 。

示例 1：
输入：num = 16
输出：true
示例 2：
输入：num = 14
输出：false
提示：

1 <= num <= 2^31 - 1

Related Topics

数学

二分查找

解法一：

二分查找

一般来说，除了 1之外，其他整数的开方后的大小都小于它的一半。

所以二分查找的时候，右边界就是整数的一半，然后二分查找，每次使用 mid的平方同 num进行比较

循环直到左边界大于右边界

class Solution {
    public boolean isPerfectSquare(int num) {
        if (num == 1) {
            return true;
        }

        int left = 0, right = num / 2;

        // 循环进行二分查找
        while (left <= right) {

            int mid = (left + right) / 2;
            // 如果符合就直接返回 true
            if (Math.pow(mid, 2) == num) {
                return true;
            } else if (Math.pow(mid, 2) > num) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }

        }

        // 全部查找完了还没找到，就返回 false
        return false;
    }
}

解法二：

数学

从数学上来看，所有的完全平方数基本都符合如下的表达式：

num= n*n =1+3+5+...+(2∗n−1)

基于此，可得如下解法

class Solution {
    public boolean isPerfectSquare(int num) {
        int x = 1;
        while (num > 0) {
            num -= x;
            x += 2;
        }
        return num == 0;
    }
}

[387] 字符串中的第一个唯一字符

给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。

示例：
s = "leetcode"
返回 0

s = "loveleetcode"
返回 2
提示：你可以假定该字符串只包含小写字母。

Related Topics

队列

哈希表

字符串

计数

解法一：

使用 LinkedHashMap<Character, Integer>，记录了字符出现的次数，同时通过 Linked有序的特点，保证先取到第一个不重复的字符

class Solution {
    public int firstUniqChar(String s) {
        if (s.length() <= 1) {
            return 0;
        }

        LinkedHashMap<Character, Integer> map = new LinkedHashMap<>();
        for (int i = 0; i < s.length(); i++) {
            map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);
        }

        for (Map.Entry<Character, Integer> characterIntegerEntry : map.entrySet()) {
            if (characterIntegerEntry.getValue().equals(1)) {
                return s.lastIndexOf(characterIntegerEntry.getKey());
            }
        }

        return -1;

    }
}

优化：

仍旧使用 HashMap，只是最后是遍历字符串，按照字符再去 map中取值

class Solution {
    public int firstUniqChar(String s) {
        if (s.length() <= 1) {
            return 0;
        }

        HashMap<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);
        }

        for (int i = 0; i < s.length(); i++) {
            if (map.get(s.charAt(i)).equals(1)) {
                return i;
            }
        }

        return -1;
    }
}

[406] 根据身高重建队列

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面正好有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

示例 2：

输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

提示：

1 <= people.length <= 2000
0 <= hi <= 106
0 <= ki < people.length
题目数据确保队列可以被重建

Related Topics

贪心

树状数组

线段树

数组

排序

解法一：

对 people进行排序，先按身高排，身高相同，按 k 排

然后直接插入

class Solution {
    public int[][] reconstructQueue(int[][] people) {
        // people[0][0] 身高多少
        // people[0][1] 前面比我高的人有多少
        Arrays.sort(people, (o1, o2) -> {
            if (o1[0] == o2[0]) {
                return o1[1] - o2[1];
            }
            return o2[0] - o1[0];
        });

        List<int[]> res = new ArrayList<>();
        for(int[] x : people) {
            res.add(x[1], x);
        }
        return res.toArray(new int[0][0]);
    }
}

[412] Fizz Buzz

给你一个整数 n ，找出从 1 到 n 各个整数的 Fizz Buzz 表示，并用字符串数组 answer（下标从 1 开始）返回结果，其中：

answer[i] == "FizzBuzz" 如果 i 同时是 3 和 5 的倍数。
answer[i] == "Fizz" 如果 i 是 3 的倍数。
answer[i] == "Buzz" 如果 i 是 5 的倍数。
answer[i] == i （以字符串形式）如果上述条件全不满足。

示例 1：

输入：n = 3
输出：["1","2","Fizz"]

示例 2：

输入：n = 5
输出：["1","2","Fizz","4","Buzz"]

示例 3：

输入：n = 15
输出：["1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"]

提示：

1 <= n <= 104

Related Topics

数学

字符串

模拟

解法一：

就按照题意

class Solution {
    public List<String> fizzBuzz(int n) {
        ArrayList<String> list = new ArrayList<>(n);
        for (int i = 1; i <= n; i++) {
            if (i % 3 == 0 && i % 5 == 0) {
                list.add("FizzBuzz");
            } else if (i % 3 == 0) {
                list.add("Fizz");
            } else if (i % 5 == 0) {
                list.add("Buzz");
            } else {
                list.add(String.valueOf(i));
            }
        }

        return list;
    }
}

[437] 路径总和Ⅲ

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
示例 2：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3
提示:

二叉树的节点个数的范围是 [0,1000]

-109 <= Node.val <= 109

-1000 <= targetSum <= 1000

Related Topics

树

深度优先搜索

二叉树

解法一：

深度优先递归，双重递归

class Solution {
    int res = 0;
    public int pathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return 0;
        }

        traverse(root, targetSum);

        pathSum(root.left, targetSum);
        pathSum(root.right, targetSum);
        
        return res;
    }

    private void traverse(TreeNode root, long targetSum) {
        if (root == null) {
            return;
        }

        if (targetSum - root.val == 0) {
            res++;
        }

        traverse(root.left, targetSum - root.val);
        traverse(root.right, targetSum - root.val);
    }
}

[448] 找到所有数组中消失的数字

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

示例 1：
输入：nums = [4,3,2,7,8,2,3,1]
输出：[5,6]
示例 2：
输入：nums = [1,1]
输出：[2]
提示：

n == nums.length

1 <= n <= 105

1 <= nums[i] <= n

进阶：你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。

Related Topics

数组

哈希表

解法一：

鸽笼思想，一共 1~N个格子，放了 1~N的数，那么只要存在的数字对应的下标变为负数即可；

但是需要保证变成负数之后，你不能彻底覆盖它的值

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        // [4, 3, 2, 7, 8, 2, 3, 1]
        // [4, 3, 2, -7, 8, 2, 3, 1]
        // [4, 3, -2, -7, 8, 2, 3, 1]
        // [4, -3, -2, -7, 8, 2, 3, 1]
        // [4, -3, -2, -7, 8, 2, -3, 1]
        // [4, -3, -2, -7, 8, 2, -3, -1]
        // [4, -3, -2, -7, 8, 2, -3, -1]
        // [4, -3, -2, -7, 8, 2, -3, -1]
        // [-4, -3, -2, -7, 8, 2, -3, -1]

        for(int x :  nums) {
            // 把理论上 x 应该在的位置变成该位置上的值的负数
            nums[Math.abs(x) - 1] = -Math.abs(nums[Math.abs(x) - 1]);
        }


        List<Integer> res = new ArrayList<>();
        for(int i = 0; i < nums.length; i++) {
            if (nums[i] > 0) {
                res.add(i + 1);
            }
        }
        return res;
    }
}

[461] 汉明距离

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

示例 1：

输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
    ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

输入：x = 3, y = 1
输出：1

提示：

0 <= x, y <= 231 - 1

Related Topics

位运算

解法一：

异或

先将 x和 y进行异或操作，得到的结果即为二者二进制表示中 0,1交错的值

然后获取该值中 1的数量即可

class Solution {
    public int hammingDistance(int x, int y) {
        int i = x ^ y;
        String s = Integer.toBinaryString(i);
        int cnt = 0;
        for (int j = 0; j < s.length(); j++) {
            if (s.charAt(j) == '1') {
                cnt++;
            }
        }
        return cnt;
    }
}

优化：直接使用 Java中的 API来统计 1的个数

class Solution {
    public int hammingDistance(int x, int y) {
        int i = x ^ y;
        return Integer.bitCount(i);
    }
}

优化：使用位运算来代替异或结果的字符串遍历

注意：i &= i-1能保证减少数字的二进制表示中的一个 1，这个 1，不是数学意义上的 -1，因为在不同位置上可能是 -2，-4，-8。。。，但是使用位运算，一定能减去一个 数字 1

class Solution {
    public int hammingDistance(int x, int y) {
        int i = x ^ y;
        int cnt = 0;
        while (i > 0) {
            cnt++;
            i &= i-1;
        }
        return cnt;
    }
}

[496] 下一个更大元素

给你两个 没有重复元素 的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。

请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。

示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
 对于 num1 中的数字 4 ，你无法在第二个数组中找到下一个更大的数字，因此输出 -1 。
 对于 num1 中的数字 1 ，第二个数组中数字1右边的下一个较大数字是 3 。
 对于 num1 中的数字 2 ，第二个数组中没有下一个更大的数字，因此输出 -1 。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
 对于 num1 中的数字 2 ，第二个数组中的下一个较大数字是 3 。
 对于 num1 中的数字 4 ，第二个数组中没有下一个更大的数字，因此输出 -1 。
提示：

1 <= nums1.length <= nums2.length <= 1000

0 <= nums1[i], nums2[i] <= 104

nums1和nums2中所有整数 互不相同

nums1 中的所有整数同样出现在 nums2 中

进阶：你可以设计一个时间复杂度为 O(nums1.length + nums2.length) 的解决方案吗？

Related Topics

栈

数组

哈希表

单调栈

解法一：

单调栈
详解见 day10: 单调队列和单调栈

class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        Stack<Integer> stack = new Stack<>();
        HashMap<Integer, Integer> map = new HashMap<>();

        // 计算 nums2中所有元素的【下一个更大值】，分别把 value:next_bigger_value存入 map中
        for (int i = nums2.length - 1; i >= 0; i--) {
            // 把栈中比当前小的值都弹出，也就是说保证此时栈要么是空的，要么 stack.peek() 更大
            while (!stack.isEmpty() && stack.peek() <= nums2[i]) {
                stack.pop();
            }
            map.put(nums2[i], stack.isEmpty() ? -1 : stack.peek());
            // 记得把自己压入单调栈
            stack.push(nums2[i]);
        }

        for (int i = 0; i < nums1.length; i++) {
            nums1[i] = map.get(nums1[i]);
        }

        return nums1;
    }
}

[509] 斐波那契数

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给你 n ，请计算 F(n) 。

示例 1：
输入：2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2：
输入：3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3：
输入：4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3
提示：

0 <= n <= 30

Related Topics

递归

记忆化搜索

数学

动态规划

解法一：

递归

class Solution {
    public int fib(int n) {
        if (n == 0) {
            return 0;
        }

        if (n == 1) {
            return 1;
        }

        return fib(n - 1) + fib(n - 2);
    }
}

解法二：

备忘录

因为前面的递归会导致绝大部分数字都会递归两遍

f(n) = f(n-1) + f(n-2) = f(n-2) + f(n-3) + f(n-3) + f(n-4) = ...

可以看到，f(n-3)会递归两遍，因此相对比较低效，添加一个缓存值的数组，可以解决

class Solution {
    public int fib(int n) {
        int[] dp = new int[n + 1];
        return helper(dp, n);
    }

    private int helper(int[] dp, int n) {
        if (n == 0 || n == 1) {
            return n;
        }

        if (dp[n] != 0) {
            return dp[n];
        }

        dp[n] = helper(dp, n - 1) + helper(dp, n - 2);
        return dp[n];
    }
}

解法三：

既然已经创建数组，就没必要再递归了

class Solution {
    public int fib(int n) {
        if (n == 0) {
            return 0;
        }

        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i < dp.length; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        return dp[n];
    }
}

优化

状态压缩，我们不需要记录每一个步骤的值，因此可以把 n压缩到 2

class Solution {
    public int fib(int n) {
        if (n == 0 || n == 1) {
            return n;
        }

        int cur = 1, prev = 0;
        for (int i = 2; i <= n; i++) {
            int sum = prev + cur;
            prev = cur;
            cur = sum;
        }

        return cur;
    }
}

[543] 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树
       1
      / \\
     2   3
    / \\     
   4   5    
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

Related Topics

树

深度优先搜索

二叉树

解法一：

后序遍历

其实就是计算最大深度，采用尾递归，将左右子树各自的最大深度求和，同 max做比较

class Solution {
    int max = 0;

    public int diameterOfBinaryTree(TreeNode root) {
        traverse(root);
        // max就是某个节点最大的左右子树深度和
        return max;
    }

    private int traverse(TreeNode root) {
        if (root == null) {
            return 0;
        }

        // 要明确函数的返回值究竟是什么？
        // 是深度，当前节点的深度，所以返回时要对左右子树的深度取更大的值
        int left = traverse(root.left);
        int right = traverse(root.right);

        // 同时在获取左右子树的深度后，更新 max值
        max = Math.max(max, left + right);
        return 1 + Math.max(left, right);
    }

}

[617] 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]
示例 2：
输入：root1 = [1], root2 = [1,2]
输出：[2,2]
提示：

两棵树中的节点数目在范围 [0, 2000] 内

-104 <= Node.val <= 104

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

解法一：

深度优先

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        return traverse(root1, root2);
    }

    private TreeNode traverse(TreeNode root1, TreeNode root2) {
        if (root1 == null) {
            return root2;
        } else if (root2 == null) {
            return root1;
        }

        // 先序遍历
        root1.val += root2.val;
        root1.left = traverse(root1.left, root2.left);
        root1.right = traverse(root1.right, root2.right);
        return root1;
    }
}

[653] 两数之和Ⅳ - 输入 BST

给定一个二叉搜索树 root 和一个目标结果 k，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。

示例 1：
输入: root = [5,3,6,2,4,null,7], k = 9
输出: true
示例 2：
输入: root = [5,3,6,2,4,null,7], k = 28
输出: false
提示:

二叉树的节点个数的范围是 [1, 104].

-104 <= Node.val <= 104

root 为二叉搜索树

-105 <= k <= 105

Related Topics

树

深度优先搜索

广度优先搜索

二叉搜索树

哈希表

双指针

二叉树

解法一：

不好的解法，没有用到 BST的更好的特性

class Solution {

    List<Integer> res = new ArrayList<>();

    public boolean findTarget(TreeNode root, int k) {
        traverse(root);
        int left = 0, right = res.size() - 1;
        while (left < right) {
            int target = res.get(left) + res.get(right);
            if (target == k) {
                return true;
            } else if (target < k) {
                left++;
            } else if (target > k) {
                right--;
            }
        }
        return false;
    }

    private void traverse(TreeNode root) {
        if (root == null) {
            return;
        }

        traverse(root.left);
        res.add(root.val);
        traverse(root.right);
    }
}

[700] 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。

例如，
给定二叉搜索树:

     4
    / \\
   2   7
  / \\
 1   3

和值: 2
你应该返回如下子树:
   2     
  / \\   
 1   3
在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

Related Topics

树

二叉搜索树

二叉树

解法一：

递归搜索二叉树，如果匹配则返回当前节点，如果root.val < val，就去其左子树找，否则去右子树找

详见 day12: 二叉搜索树基础

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        // base case
        if (root == null) {
            return null;
        }
        
        if (root.val == val) {
            return root;
        } else if (root.val > val) {
            return searchBST(root.left, val);
        } else {
            return searchBST(root.right, val);
        }
    }
}

[859] 亲密字符串

给你两个字符串 s 和 goal ，只要我们可以通过交换 s 中的两个字母得到与 goal 相等的结果，就返回 true ；否则返回 false 。

交换字母的定义是：取两个下标 i 和 j （下标从 0 开始）且满足 i != j ，接着交换 s[i] 和 s[j] 处的字符。

例如，在 "abcd" 中交换下标 0 和下标 2 的元素可以生成 "cbad" 。

示例 1：

输入：s = "ab", goal = "ba"
输出：true
解释：你可以交换 s[0] = 'a' 和 s[1] = 'b' 生成 "ba"，此时 s 和 goal 相等。

示例 2：

输入：s = "ab", goal = "ab"
输出：false
解释：你只能交换 s[0] = 'a' 和 s[1] = 'b' 生成 "ba"，此时 s 和 goal 不相等。

示例 3：

输入：s = "aa", goal = "aa"
输出：true
解释：你可以交换 s[0] = 'a' 和 s[1] = 'a' 生成 "aa"，此时 s 和 goal 相等。

示例 4：

输入：s = "aaaaaaabc", goal = "aaaaaaacb"
输出：true

提示：

1 <= s.length, goal.length <= 2 * 104
s 和 goal 由小写英文字母组成

Related Topics

哈希表

字符串

解法一：

遍历两个字符串，寻找并记录，字符串中不同的字符的位置，只要记录两个就行了，同时将每个字符串扔到 HashSet中

然后进行判断：

不存在不同，且 HashSet的 size < 字符串长度，则说明有重复的字符，一定可以；否则就会出现 s=“ab”, goal=“ab”的情况，这个时候返回false，即只需要判断 set.size != s.length()
存在不同，则把两个字符交换位置，然后对新组成的字符串进行比较

class Solution {
    public boolean buddyStrings(String s, String goal) {

        char[] sArr = s.toCharArray();
        char[] gArr = goal.toCharArray();
        int i = 0, j = 0, count = 0;
        HashSet<Character> set = new HashSet<>();
        // 遍历找不同的字符，并记录位置
        for (int k = 0; k < s.length(); k++) {
            if (sArr[k] != gArr[k]) {
                if (count == 0) {
                    i = k;
                    count++;
                } else if (count == 1) {
                    j = k;
                    count++;
                } else {
                    break;
                }
            }
        }

        // 如果没有不同，就往 HashSet里面塞
       if (count == 0) {
            for (char c : sArr) {
                // 一旦发现塞重复了，就返回true
                if (!set.add(c)) {
                    return true;
                }
            }
            return false;
        }

		// 如果存在不同
        char tmp = sArr[i];
        sArr[i] = sArr[j];
        sArr[j] = tmp;
        return new String(sArr).equals(goal);

    }
}

稍微优化一点，把塞进 HashSet的步骤往前移动

class Solution {

    public boolean buddyStrings(String s, String goal) {

        char[] sArr = s.toCharArray();
        char[] gArr = goal.toCharArray();

        HashSet<Character> set = new HashSet<>();
        if (s.equals(goal)) {
            for (char c : sArr) {
                if (!set.add(c)) {
                    return true;
                }
            }
            return false;
        }

        int i = 0, j = 0, count = 0;
        for (int k = 0; k < s.length(); k++) {
            if (sArr[k] != gArr[k]) {
                if (count == 0) {
                    i = k;
                    count++;
                } else if (count == 1) {
                    j = k;
                    count++;
                } else {
                    break;
                }
            }
        }

        char tmp = sArr[i];
        sArr[i] = sArr[j];
        sArr[j] = tmp;
        return new String(sArr).equals(goal);

    }
}

看看力扣官方的题解

class Solution {
    public boolean buddyStrings(String s, String goal) {
        // 先判断长度
        if (s.length() != goal.length()) {
            return false;
        }

        // 这里用了一个数组来表示是否存在重复，s.charAt(i) - 'a'刚好可以定位到长度为 26的数组内部
        if (s.equals(goal)) {
            int[] cnt = new int[26];
            for (char c : s.toCharArray()) {
                cnt[c - 'a']++;
                if (cnt[c - 'a'] >= 2) {
                    return true;
                }
            }

            return false;
        }

        // 其他情况遍历
       int first = -1, last = -1;
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == goal.charAt(i)) {
                continue;
            }

            if (first == -1) {
                first = i;
            } else if (last == -1) {
                last = i;
            } else {
                // 如果出现了 3处及以上的不同，那么就直接返回 false
                return false;
            }
        }

        return last != -1
                && s.charAt(last) == goal.charAt(first)
                && s.charAt(first) == goal.charAt(last);
    }

[704] 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示：

你可以假设 nums 中的所有元素是不重复的。

n 将在 [1, 10000]之间。

nums 的每个元素都将在 [-9999, 9999]之间。

Related Topics

数组

二分查找

解法一：

二分查找

class Solution {
    public int search(int[] nums, int target) {

        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            }
        }
        return -1;
    }
}

[876] 链表的中间结点

给定一个头结点为 head 的非空单链表，返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.

示例 2：

输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])
由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。

提示：

给定链表的结点数介于 1 和 100 之间。

Related Topics

链表

双指针

解法一：

快慢指针，快指针每次都两格，慢指针每次走一格，当快指针走到链表末尾的时候，慢指针恰好在链表中间（如果链表个数是偶数个，就会在中间靠后的那一个地方）

class Solution {
    public ListNode middleNode(ListNode head) {

        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
}

[1047] 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

提示：

1 <= S.length <= 20000
S 仅由小写英文字母组成。

Related Topics

栈

字符串

解法一：

将字符串看作字符数组，就变成了字符数组去重

class Solution {
    public String removeDuplicates(String s) {
        char[] arr = s.toCharArray();
        int idx = -1;
        for (int i = 0; i < s.length(); i++) {
            if (idx == -1 || arr[idx] != arr[i]) {
                arr[++idx] = arr[i];
            } else {
                idx--;
            }
        }

        return new String(arr, 0, idx + 1);
    }
}

[1480] 一维数组的动态和

给你一个数组 nums 。数组「动态和」的计算公式为：runningSum[i] = sum(nums[0]…nums[i]) 。

请返回 nums 的动态和。

示例 1：

输入：nums = [1,2,3,4]
输出：[1,3,6,10]
解释：动态和计算过程为 [1, 1+2, 1+2+3, 1+2+3+4] 。

示例 2：

输入：nums = [1,1,1,1,1]
输出：[1,2,3,4,5]
解释：动态和计算过程为 [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1] 。

示例 3：

输入：nums = [3,1,2,10,1]
输出：[3,4,6,16,17]

提示：

1 <= nums.length <= 1000
-10^6 <= nums[i] <= 10^6

Related Topics

数组

前缀和

解法一：

前缀和

class Solution {
    public int[] runningSum(int[] nums) {
        int[] res = new int[nums.length];
        res[0] = nums[0];
        for(int i = 1; i < nums.length; i++) {
            res[i] = res[i-1] + nums[i];
        }

        return res;
    }
}

♥ [1893] 检查是否区域内所有整数都被覆盖

给你一个二维整数数组 ranges 和两个整数 left 和 right 。每个 ranges[i] = [starti, endi] 表示一个从 starti 到 endi 的 闭区间 。

如果闭区间 [left, right] 内每个整数都被 ranges 中 至少一个 区间覆盖，那么请你返回 true ，否则返回 false 。

已知区间 ranges[i] = [starti, endi] ，如果整数 x 满足 starti <= x <= endi ，那么我们称整数x 被覆盖了。

示例 1：

输入：ranges = [[1,2],[3,4],[5,6]], left = 2, right = 5
输出：true
解释：2 到 5 的每个整数都被覆盖了：
- 2 被第一个区间覆盖。
- 3 和 4 被第二个区间覆盖。
- 5 被第三个区间覆盖。

示例 2：

输入：ranges = [[1,10],[10,20]], left = 21, right = 21
输出：false
解释：21 没有被任何一个区间覆盖。

提示：

1 <= ranges.length <= 50
1 <= starti <= endi <= 50
1 <= left <= right <= 50

Related Topics

数组

哈希表

前缀和

解法一

位示图

使用 boolean[] 数组构建一个类似位示图的指示数组，凡事在 range范围内的都是 true，范围外的都是 false

在 left ~ right范围内遍历 boolean数组，一旦遇到了 false，就返回 false；否则全部遍历结束再返回 true

class Solution {
    public boolean isCovered(int[][] ranges, int left, int right) {
        // range中的最大值
        int big = -1;
        // range中的最小值
        int small = -1;
        // 遍历ranges，获取最值
        for (int[] range : ranges) {
            big = range[1] > big ? range[1] : big;
        }
        // 如果 [left, right]不是包涵在 [small, big]范围内，那肯定是有没覆盖到的数据，返回 false
        if (left < small || right > big) {
            return false;
        }
        int len = big - small;

        // 初始化一个位示图，boolean默认就是 false
        boolean[] arr = new boolean[len + 1];

        // 根据每个 range的范围，在位示图中赋值为 true
        // 注意，因为是闭区间，所以位示图的下限要 +1
        for (int[] range : ranges) {
            Arrays.fill(arr, range[0] - small, range[1] - small + 1, true);
        }

        // 遍历位示图，如果在有 false，就返回 false
        for (int i = left - small; i <= right - small; i++) {
            if (arr[i] == false) {
                return false;
            }
        }
        return true;
    }
}

解法二

基于排序

将区间的起始点从小到大排序，然后每次比较，若 l < left < r，那么可知在 [left, r]范围内已经覆盖；

然后另 left = r + 1，如果最后 left可以超过 right则区间全部覆盖，返回 true

class Solution {
    public boolean isCoverd(int[][] ranges, int left, int right) {
        // 先排序
        Arrays.sort(ranges, (a, b) -> {
            return a[0] - b[0];
        });

        // 修改 left值
        for (int[] range : ranges) {
            int cLeft = range[0];
            int cRight = range[1];
            
            if (cLeft <= left && left <= cRight) {
                left = cRight + 1;
            }
        }

        return left > right;
    }
}

解法三：

差分数组

class Solution {
    public boolean isCovered(int[][] ranges, int left, int right) {
        int[] arr = new int[52];
        // arr数组中的结果可能是：0 0 0 1 0 0 0 -1 0 0 1 0 0 0 -1 ...
        // 此时在 left和 right范围内存在部分值不被 range包裹
        for (int[] range : ranges) {
            arr[range[0]]++;
            arr[range[1] + 1]--;
        }

        int res = 0;
        for (int i = 0; i < arr.length; i++) {
            res += arr[i];
            if (i >= left && i <= right && res <= 0) {
                return false;
            }
        }

        return true;
    }
}

[剑指 Offer 03] 数组中重复的数字

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：
输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3 
限制：
2 <= n <= 100000
Related Topics

数组

哈希表

排序

解法一：

HashSet

class Solution {
    public int findRepeatNumber(int[] nums) {
        HashSet<Integer> set = new HashSet<>();
        for(int x : nums) {
            if(!set.add(x)) {
                return x;
            }
        }

        return -1;
    }
}

解法二：

原地交换

class Solution {
    public int findRepeatNumber(int[] nums) {
        for(int i = 0; i<nums.length; i++) {
            // 如果刚好就在这里，那么不管
            if(nums[i] == i) {
                continue;
            }

            int cur = nums[i];
            int posVal = nums[cur];
            // 如果目标位置上的和当前的值一样，就认为是有问题的
            if(cur == nums[cur]) {
                return cur;
            }

            nums[i] = nums[cur];
            nums[cur] = cur;
        }

        return nums[nums.length-1];
    }
}

[剑指 Offer 53-I] 在排序数组中查找数字

统计一个数字在排序数组中出现的次数。

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

0 <= 数组长度 <= 50000

解法一

使用 ArrayList的 indexOf()和 lastIndexOf()方法

class Solution {
    public int search(int[] nums, int target) {
        ArrayList<Integer> list = new ArrayList<>();
        for (int i : nums) {
            list.add(i);
        }

        int i = list.indexOf(target);
        if (i == -1)
            return 0;
        int j = list.lastIndexOf(target);
        return j - i + 1;
    }
}

或者自己手写 indexOf()的实现，遍历数组也可以

class Solution {
    public int search(int[] nums, int target) {
        int len = nums.length;
        int i = -1, j = -1;
        for (i = 0; i < len && target != nums[i]; i++) {
        }
        if (i >= len) {
            return 0;
        }
        for (j = len - 1; j >= 0 && target != nums[j]; j--){
            
        }
        return j - i + 1;
    }
}

解法二

先确定一边，然后逐个往前或者往后数

class Solution {
    public int search(int[] nums, int target) {
        int len = nums.length;
        int l = 0, r = len - 1;
        int mid = -1;
        while(l < r) {
            mid = (l + r + 1) >> 1;
            if(nums[mid] <= target) {
                l = mid;
            }
            else r = mid - 1;
        }
        int ans = 0;
        while(r >= 0 && nums[r] == target && r-- >= 0) {
            ans++;
        }
        return ans;
    }
}

解法三

二分查找数组中的元素，相比于原来从头开始找效率高一些

class Solution {
    public int search(int[] nums, int target) {
        int len = nums.length;
        int i = binarySearch(nums, 0, len - 1, target, true);
        if (i < 0) {
            return 0;
        }
        int j = binarySearch(nums, 0, len - 1, target, false);
        return j - i + 1;
    }

    public static int binarySearch(int[] nums, int start, int end, int target, boolean first) {
        int mid = -1;
        while (start <= end) {
            mid = (start + end) / 2;
            if (nums[mid] == target) {
                if (first == true && mid - 1 >= 0 && nums[mid - 1] == target) {
                    end = mid - 1;
                    continue;
                } else if (first == false && mid + 1 < nums.length && nums[mid + 1] == target) {
                    start = mid + 1;
                    continue;
                }
                return mid;
            } else if (nums[mid] < target) {
                start = mid + 1;
            } else if (nums[mid] > target) {
                end = mid - 1;
            }
        }
        return -1;
    }
}

中等难度

[2] 两数相加

给出两个非空的链表用来表示两个非负的整数。其中，它们各自的位数是按照逆序的方式存储的，并且它们的每个节点只能存储一位数字。

我们将这两个数相加起来，则会返回一个新的链表来表示它们的和

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)

输出：7 -> 0 -> 8

解法一：

使用 BigInteger的运算，先从链表中获取数据，然后进行计算，最后再生成一个新链表。

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        StringBuilder n1 = new StringBuilder();
        StringBuilder n2 = new StringBuilder();
        ListNode p = l1, q = l2;

        while (p != null) {
            n1.append(p.val + "");
            p = p.next;

        }
        n1 = n1.reverse();

        while (q != null) {
            n2.append(q.val + "");
            q = q.next;

        }
        n2 = n2.reverse();

        BigInteger m1 = new BigInteger(n1.toString());
        BigInteger m2 = new BigInteger(n2.toString());

        BigInteger val = m1.add(m2);

        char[] vals = val.toString().toCharArray();
        int len = vals.length;
        ListNode l3 = new ListNode(Integer.parseInt(String.valueOf(vals[len - 1])));
        for (int k = 0; k < len - 1; k++) {
            ListNode m = new ListNode(Integer.parseInt(String.valueOf(vals[k])));
            m.next = l3.next;
            l3.next = m;
        }

        return l3;

    }
}

解法二：

针对每个位次进行求和，并与当前位置的进位值相加。

如果两个链表长度不同，短的那部分就用 0 来替换

在遍历结束后，判断最后有没有进位，如果有，就再加一个结点

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        int lastVal = 0;
        // dummy节点
        ListNode head = new ListNode(0), p = head;

        while (l1 != null || l2 != null) {
            int v1 = l1 == null ? 0 : l1.val;
            int v2 = l2 == null ? 0 : l2.val;
            int sum = v1 + lastVal + v2;

            // 进位值
            lastVal = sum / 10;
            // 实际该位上的值
            sum = sum % 10;

            p.next = new ListNode(sum);
            p = p.next;
            if (l1 != null) {
                l1 = l1.next;
            }
            if (l2 != null) {
                l2 = l2.next;
            }
        }

        if (lastVal > 0) {
            p.next = new ListNode(lastVal);
        }

        return head.next;
    }
}

[3] 无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
  请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

示例 4:

输入: s = ""
输出: 0

提示：

0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成

Related Topics

哈希表

字符串

滑动窗口

解法一：

采用HashMap存储每个子串中的字符，键为字符，值为出现的位置

这个 map里的数据只会增加，不会减少，因此 left的定位不能简单的 map.get()+1，因为你 contansKey为 true，并不一定意味着它在窗口内。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s == null || s.length() == 0) {
            return 0;
        }

        // map中记录 字符 和 下标
        HashMap<Character, Integer> map = new HashMap<>();
        int left = 0, right = 0, max = 0;

        while (right < s.length()) {
            char rChar = s.charAt(right);
            if (map.containsKey(rChar)) {
                // abba，当 right到 abba时，窗口中此时只有 b left=2，但 map.get(a) = 0
                left = Math.max(left, map.get(rChar) + 1);
            }

            map.put(rChar, right);
            max = Math.max(max, right - left + 1);
            right++;
        }

        return max;
    }
}

使用算法训练营中给的模板进行解答，这个和下面的 hashset一样，都是 O(N²)

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 声明窗口
        HashMap<Character, Integer> window = new HashMap<>();

        // 左右边界
        int left = 0, right = 0;
        // 结果值
        int res = 0;

        // 开始滑动
        while (right < s.length()) {
            // 获取右边界值
            char rightChar = s.charAt(right);
            // 右边界右移
            right++;
            // 将右边界放入窗口中
            window.put(rightChar, window.getOrDefault(rightChar, 0) + 1);

            // 如果该字符重复了
            while (window.get(rightChar) > 1) {
                // 获取左边界字符
                char leftChar = s.charAt(left);
                // 左边界右移，窗口变小
                left++;
                // 窗口中减少一个左边界字符
                window.put(leftChar, window.getOrDefault(leftChar, 0) - 1);
            }

            // 完成上面那个 while之后，此时窗口内一定是符合当时的 无重复字符的最长子串的状况，所以可以对 res进行更新
            res = Math.max(res, right - left);
        }

        // 返回结果值
        return res;
    }
}

解法二：

采用HashSet存储单个字符

首次出现的字符添加
已有字符出现时，删除最早的字符

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 哈希集合，记录每个字符是否出现过
        Set<Character> occ = new HashSet<Character>();
        int n = s.length();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = 0, ans = 0;
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.remove(s.charAt(i - 1));
            }
            while (rk < n && !occ.contains(s.charAt(rk))) {
                // 不断地移动右指针
                occ.add(s.charAt(rk));
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = Math.max(ans, rk - i);
        }
        return ans;
    }
}

第二次手写

class Solution {
    public int lengthOfLongestSubstring(String s) {
        HashSet<Character> window = new HashSet<>();
        int res = 0;
        int left = 0, right = 0;
        
        while(right < s.length()) {
            char in = s.charAt(right);
            right++;

            while(window.contains(in)) {
                char out = s.charAt(left);
                left++;
                window.remove(out);
            }

            window.add(in);
            res = Math.max(res, window.size());
        }

        return res;
    }
}

[5] 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。
示例 2：
输入：s = "cbbd"
输出："bb"
示例 3：
输入：s = "a"
输出："a"
示例 4：
输入：s = "ac"
输出："a"
提示：

1 <= s.length <= 1000

s 仅由数字和英文字母（大写和/或小写）组成

Related Topics

字符串

动态规划

解法一：

中心扩散法

枚举所有可能的回文子串的中心位置
中心位置可能是一个字符也可能是两个
记录最长回文子串的相关变量

class Solution {
    String res = "";
    
    public String longestPalindrome(String s) {
        if (s.length() == 1) {
            return s;
        }

        
        for(int i = 0; i < s.length(); i++) {
            // aba是回文串，abba也是回文串，为了方便处理奇偶数，这里必须传 left、right
            traverse(s, i, i);
            traverse(s, i, i + 1);    
        }

        return res;
    }

    private void traverse(String s, int left, int right) {
        // 注意边界条件
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            left--;
            right++;
        }

        String tmp = s.substring(left+1, right);
        res = res.length() > tmp.length() ? res : tmp;
    }
}

❤ 解法二：

动态规划

如果一个字符串是回文串，那么它去掉左右两端字符后依旧是回文串
- 状态：dp[i][j] 表示子串 s[i..j]是否为回文子串
- 得到状态转移方程：dp[i][j] = (s[i] == s[j]) && dp[i+1][j-1]
- 边界条件：j - 1 - (i + 1) +1 < 2，整理得：j - i < 3
- 初始化：dp[i][i] = true，对角线上元素，即长度为1的子串一定是满足条件的
- 输出：在得到一个状态的值为 true 的时候，记录起始位置和长度，填表完成以后再截取

class Solution {
    public String longestPalindrome(String s) {
        if (s.length() <= 1) {
            return s;
        }

        // dp[i][j]表示字符串从 i 到 j 是否构成回文
        boolean[][] dp = new boolean[s.length()][s.length()];
        for (int i = 0; i < dp.length; i++) {
            dp[i][i] = true;
        }

        int begin = 0, maxLen = 1;
        // 注意内外层的顺序
        for (int j = 1; j < dp.length; j++) {
            for (int i = 0; i < j; i++) {
                // 如果连两端都不相等，i到j 肯定不是回文的
                if (s.charAt(i) != s.charAt(j)) {
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                if (dp[i][j] && j - i + 1 > maxLen) {
                    begin = i;
                    maxLen = j - i + 1;
                }
            }
        }

        return s.substring(begin, begin + maxLen);
    }
}

解法三：

Manacher算法

专门用于查找最长回文子串的算法，复杂度为O(n)

相对复杂，绝大多数面试和笔试不做要求
将原始字符串进行预处理，在预处理之后的字符串上执行动态规划和中心扩散方法
为了将奇偶数回文串统一表示，将原始字符串进行预处理，用不在输入字符串中的字符隔开

[6] Z 字形变换

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

P A H N
A P L S I I G
Y I R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。

请你实现这个将字符串进行指定行数变换的函数：
string convert(string s, int numRows);

输入：s = "PAYPALISHIRING", numRows = 3
输出："PAHNAPLSIIGYIR"

输入：s = "PAYPALISHIRING", numRows = 4
输出："PINALSIGYAHRPI"
解释：
P I N
A L S I G
Y A H R
P I

输入：s = "A", numRows = 1
输出："A"

解法一

针对每一行，创建一个 ArrayList<Character>，并且把它作为 Value，以当前的行数作为键，存放在 HashMap中

HashMap<Integer, ArrayList<Character>>

遍历整个字符串中的每一个字符，设置好相关的循环遍历和循环方向判断变量，将每个字符都放入对应的列表中

class Solution {
    public String convert(String s, int numRows) {
        // 如果只有一列的，直接返回就行
        if (numRows == 1) {
            return s;
        }

        // 创建好 Map，每一行对应 一个 ArrayList，都存在 Map中
        HashMap<Integer, ArrayList<Character>> map = new HashMap<>();
        for (int i = 1; i <= numRows; i++) {
            map.put(new Integer(i), new ArrayList<Character>());
        }

        char[] arr = s.toCharArray();
        // 当前的行数
        int round = 1;
        // 判断是向上遍历还是向下遍历
        boolean down = true;

        // 遍历字符串中的每一个字符
        for (char c : arr) {
            // 根据行数添加到指定的列表中
            ArrayList<Character> list = map.get(round);
            list.add(c);

            // 判断 如果向下遍历，行数增加；如果向上遍历，行数减少
            if (down) {
                round++;
            } else {
                round--;
            }

            // 如果向下遍历到最大行数了，就转为向上遍历
            if (down && round == numRows) {
                down = false;
                // 同理，如果向上遍历到第一行了，就转为向下遍历
            } else if (!down && round == 1) {
                down = true;
            }
        }

        // 获取出每一个字符，拼接起来
        StringBuilder sb = new StringBuilder();
        for (ArrayList<Character> value : map.values()) {
            for (Character s1 : value) {
                sb.append(s1);
            }
        }

        // 返回得到的字符串
        return sb.toString();
    }
}

解法二

思路同上一样，只是不用 ArrayList了，直接就用 StringBuilder就行

class Solution {
    public String convert(String s, int numRows) {
        if(numRows == 1) {
            return s;
        }

        List<StringBuilder> rows = new ArrayList<>();
        for (int i = 0; i < numRows; i++) {
            rows.add(new StringBuilder());
        }

        int curRow = 0;
        boolean goingDown = false;

        for (char c : s.toCharArray()) {
            rows.get(curRow).append(c);
            if (curRow == 0 || curRow == numRow - 1) {
                goingDown = !goingDown;
            }
            curRow += goingDown ? 1 : -1;
        }

        StringBuilder ret = new StringBuilder();
        for(StringBuilder e : rows) {
            ret.append(e);
        }

        return ret.toString();
    }
}

[8] 字符串转换整数(atoi)

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。

函数 myAtoi(string s) 的算法如下：

读入字符串并丢弃无用的前导空格
检查下一个字符（假设还未到字符末尾）为正还是负号，读取该字符（如果有）。确定最终结果是负数还是正数。如果两者都不存在，则假定结果为正。
读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数（即，"123" -> 123， "0032" -> 32）。如果没有读入数字，则整数为 0 。必要时更改符号（从步骤
2 开始）。
如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被固
定为 −231 ，大于 231 − 1 的整数应该被固定为 231 − 1 。
返回整数作为最终结果。

注意：

本题中的空白字符只包括空格字符 ' ' 。
除前导空格或数字后的其余字符串外，请勿忽略任何其他字符。

解法一

先规整字符串，把前面带字母的、前面带0的都休整好，该返回 0的就返回0

判断长度，长度差不多，就先试着转成 Long，再把 Long数和 Integer.MaxValue对比

结果返回

class Solution {
    public int myAtoi(String s) {
        // 去空格
        s = s.trim();
        if (s == null || s.isEmpty()) {
            return 0;
        }

        // 判断正负，并且先把符号给去掉
        boolean positive = true;
        if (s.startsWith("-")) {
            positive = false;
            s = s.substring(1, s.length());
        } else if (s.startsWith("+")) {
            positive = true;
            s = s.substring(1, s.length());
        }

        // 剔除字符串前面的 0
        while (s != null && s.startsWith("0")) {
            s = s.substring(1, s.length());
        }

        StringBuilder sb = new StringBuilder();
        // 遍历每个字符，如果是数字就ok，如果是字符就退出
        for (Character c : s.toCharArray()) {
            if (Character.isDigit(c)) {
                sb.append(c);
            } else {
                break;
            }
        }
        s = sb.toString();

        // 先比较长度
        if (s.length() > 15) {
            return positive ? Integer.MAX_VALUE : Integer.MIN_VALUE;
        }

        if (s == null || s.isEmpty()) {
            return 0;
        }
        // 先转换为 long，再让 long和 int的最大值比较
        Long aLong = Long.valueOf(s);
        if (aLong > Integer.MAX_VALUE) {
            return positive ? Integer.MAX_VALUE : Integer.MIN_VALUE;
        }
        return positive ? new Integer(s) : 0 - new Integer(s);
    }
}

解法二

自动机

字符串处理的题目往往涉及复杂的流程以及条件情况，为了有条理的分析每个输入的字符的情况，可以使用自动机的概念

程序在每个时刻有一个状态 s，每次从序列中输入一个字符 c，并根据字符 c转移到下一个状态 s'

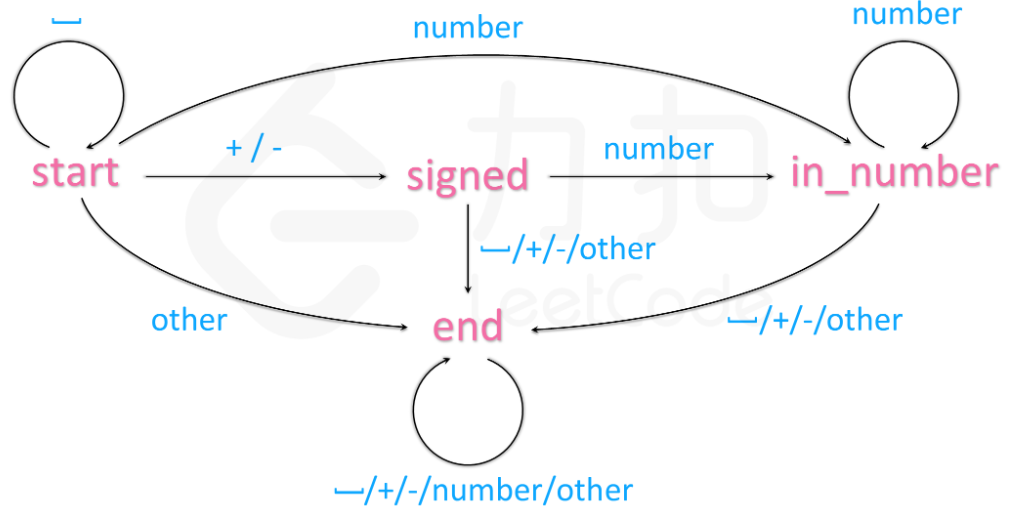
另外自动机也需要记录当前已经输入的数字，只要在 s' 为 in_number时，更新我们输入的数字即可。

class Automaton {
    public int sign = 1;
    public long ans = 0;
    private String state = "start";
    // 定义自动机的状态
    private Map<String, String[]> table = new HashMap<String, String[]>() {{
        put("start", new String[]{"start", "signed", "in_number", "end"});
        put("signed", new String[]{"end", "end", "in_number", "end"});
        put("in_number", new String[]{"end", "end", "in_number", "end"});
        put("end", new String[]{"end", "end", "end", "end"});
    }};

    public void get(char c) {
        // 根据传入的字符，获取对应的值的状态
        // 如果 一旦end了，之后不管再给什么值都没用了，因为 end对于的数组里面都是 end
        state = table.get(state)[get_col(c)];
        if ("in_number".equals(state)) {
            // 记录数字的具体的值
            ans = ans * 10 + c - '0';
            ans = sign == 1 ? Math.min(ans, (long) Integer.MAX_VALUE) : Math.min(ans, -(long) Integer.MIN_VALUE);
        } else if ("signed".equals(state)) {
            // 记录数字的符号
            sign = c == "+" ? 1 : -1;
        }
    }

    // 判断如果是 空格返回0；如果是 加减号返回 1；如果是数字返回2；如果是其他的返回3
    private int get_col(char c) {
        if (c == ' ') {
            return 0;
        }
        if (c == '+' || c == '-') {
            return 1;
        }
        if (Character.isDigit(c)) {
            return 2;
        }
        return 3;
    }
}

[11] 盛最多水的容器

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。

在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

输入：height = [1,1]
输出：1

输入：height = [4,3,2,1,4]
输出：16

输入：height = [1,2,1]
输出：2

解法一：

双指针

通过分析，我们可以发现：

如果现在两条垂直线分别位于左右两侧，那么其面积 = 短线长度 * 间距
之后，为了获取更大的面积，我们肯定会移动垂直线
1. 移动长的那一根，移动之后，如果遇到更长的，那么面积变化只跟间距有关，如果遇到更短的，短线长度可能变小
2. 移动短的那一根，移动之后，如果遇到更长的，面积可能变大，遇到更小的面积可能变小
为了保证每次移动之后，获取的面积尽可能只与短线长度有关，我们设置初始的两条短线分别从最左侧和最右侧开始。
故最终的情况为：
- 线 A从左侧开始，线 B从右侧开始，先记录当前的面积；
- 短的那根线向中心移动，长的那根线不动
- 重新计算面积
- 如此反复直到曾经的左线大于右线

class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length - 1, res = 0;
        while(i < j){
            res = height[i] < height[j] ?
                    Math.max(res, (j - i) * height[i++]):
                    Math.max(res, (j - i) * height[j--]);
        }
        return res;
    }
}

[12] 整数转罗马数字

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000

例如:

2 写做 II ，即为两个并列的 1。
12 写做 XII ，即为 X + II 。
27 写做 XXVII，即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。

数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。

这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给你一个整数，将其转为罗马数字。

输入: num = 3
输出: "III"

输入: num = 4
输出: "IV"

输入: num = 9
输出: "IX"

输入: num = 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.

输入: num = 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.

解法一：

将罗马数字和对应的中文数字存到一个 LinkedHashMap<Integer, Character> map中，内部是数字从大到小排序。

遍历整个 map，每次都从第一个键开始遍历，当发现获取的键比 num小时，num -= key，str += map.get(key)

然后，针对罗马数字中的特殊规则，我们获取当前数字的去除位数版，如：987 -> 900，并逐个 if判断，它是否符合特殊规则

class Solution {
    public String intToRoman(int num) {
        // 将罗马数字添加到 map中
        LinkedHashMap<Integer, Character> map = new LinkedHashMap<>();
        map.put(new Integer(1000), new Character('M'));
        map.put(new Integer(500), new Character('D'));
        map.put(new Integer(100), new Character('C'));
        map.put(new Integer(50), new Character('L'));
        map.put(new Integer(10), new Character('X'));
        map.put(new Integer(5), new Character('V'));
        map.put(new Integer(1), new Character('I'));

        // 待返回的字符串
        StringBuilder value = new StringBuilder();
        int cal = 0;

        while (num > 0) {

            // 获取去除了尾数后的值
            cal = getRoundValue(num);

            // 遍历 map
            for (Integer integer : map.keySet()) {
                // 先判断是不是符合特殊情况
                if (cal + 1 == integer) {
                    value.append("I" + map.get(integer));
                    num -= cal;
                    break;
                } else if (cal + 10 == integer) {
                    value.append("X" + map.get(integer));
                    num -= cal;
                    break;
                } else if (cal + 100 == integer) {
                    value.append("C" + map.get(integer));
                    num -= cal;
                    break;
                } else if (num >= integer) {
                    value.append(map.get(integer));
                    num -= integer;
                    break;
                }
            }
        }
        return value.toString();
    }


    private int getRoundValue(int num) {
        int len = (num + "").length();
        return num - num % (int) Math.pow(10, len - 1);
    }
}

解法二：

省去判断的成本，直接在 map中添加各种特殊情况

class Solution {
    public String intToRoman(int num) {
        LinkedHashMap<Integer, String> map = new LinkedHashMap<>();
        map.put(new Integer(1000), "M");
        map.put(new Integer(900), "CM");
        map.put(new Integer(500), "D");
        map.put(new Integer(400), "CD");
        map.put(new Integer(100), "C");
        map.put(new Integer(90), "XC");
        map.put(new Integer(50), "L");
        map.put(new Integer(40), "XL");
        map.put(new Integer(10), "X");
        map.put(new Integer(9), "IX");
        map.put(new Integer(5), "V");
        map.put(new Integer(4), "IV");
        map.put(new Integer(1), "I");

        String vale = "";
        while (num > 0) {
            for (Integer integer : map.keySet()) {
                if (num >= integer) {
                    vale += map.get(integer);
                    num -= integer;
                    break;
                }
            }
        }
        return vale;
    }
}

解法三：

贪心算法

其实就是把外层循环和内层循环互换，使用两个数组代替 LinkedHashMap

class Solution {
    public String intToRoman(int num) {
        int[] nums = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
        String[] romans = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};

        StringBuilder sb = new StringBuilder();
        int index = 0;
        while(index < 13) {
            while(num >= nums[index]) {
                sb.append(romans[index]);
                num -= nums[index];
            }
            index ++;
        }
        return sb.toString();
    }
}

[15] 三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

输入：nums = []
输出：[]

输入：nums = [0]
输出：[]

解法一

先对数组排序，然后因为要求三数和为 0，故：

第一个数必定小于 0
第二个数可正可负，如果是正一定小于第一个数的绝对值的一半
第三个数一定是正

当然，也有特殊情况就是三个零

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        LinkedHashSet<List<Integer>> ans = new LinkedHashSet<>();
        // 如果数组长度小于三，就返回一个空列表
        if (nums.length < 3) {
            return new ArrayList<List<Integer>>(ans);
        }
        Arrays.sort(nums);


        for (int i = 0; i < nums.length - 2; i++) {
            // 遍历到大于零就退出，遍历到零就判断后面几个是不是零
            if (nums[i] >= 0) {
                if (nums[i] == 0 && nums.length >= i + 3 && nums[i + 2] == 0)
                    ans.add(Arrays.asList(0, 0, 0));
                break;
            }
            // 定位第二个数可能的范围
            int jc = Arrays.binarySearch(nums, -nums[i] / 2);
            jc = jc > 0 ? jc : -jc - 2;
            // 遍历第二个数
            for (int j = i + 1; j <= jc; j++) {

                // 遍历第三个数
                int q = Arrays.binarySearch(nums, j + 1, nums.length, -(nums[i] + nums[j]));

                // 通过 HashSet保证不重复
                if (q > 0) {
                    ans.add(Arrays.asList(nums[i], nums[j], -(nums[i] + nums[j])));
                }
            }
        }

        // 再以列表的形式返回
        return new ArrayList<List<Integer>>(ans);
    }
}

解法二：

双指针

正常情况下肯定是要 O(n³)，但是我们可以发现，当第二个数变大的时候，第三个数肯定是在变小的，并且是在上一次位置之后变小。

那么就可以退化到 O(n²)了

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<List<Integer>>();

        for (int a = 0; i < nums.length; a++) {
            if (a > 0 && nums[a] == nums[a - 1])
                continue;

            int c = nums.length - 1;
            for (int b = i + 1; b < n; b++) {
                if (b > 0 && nums[b] == nums[b - 1])
                    continue;

                while(b < c && nums[b] + nums[c] + nums[a] > 0)
                    c--;
                if (c == b)
                    break;

                if (nums[b] + nums[c] + nums[a] == 0) {
                    ans.add(Arrays.asList(nums[a], nums[b], nums[c]));
                }
            }
        }
        return ans;
    }
}

[16] 最接近的三数之和

给定一个包括 n 个整数的数组 nums 和一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

示例：
输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
提示：

3 <= nums.length <= 10^3

-10^3 <= nums[i] <= 10^3

-10^4 <= target <= 10^4

Related Topics

数组

双指针

排序

解法一：

双指针 + 排序

先对数组进行排序，然后从左到右依次枚举取值 a，在剩下的右侧区间内，最左边的是 b，最右边的是 c

如果 a+b+c == target就返回，否则如果 < target，b取区间内的后一个值，如果> target，c取区间内的前一个值，同时比较当前 sum 同 target的差值，更新 res

class Solution {
    public int threeSumClosest(int[] nums, int target) {

        // 先排序
        Arrays.sort(nums);
        int res = 100001;
        int left, right, sum;

        // 先固定 i
        for (int i = 0; i < nums.length; i++) {
            left = i + 1;
            right = nums.length - 1;

            // 获取当前的三数和，同 target进行比较
            while (left < right) {
                sum = nums[i] + nums[left] + nums[right];

                if (Math.abs(target - sum) < Math.abs(target - res)) {
                    res = sum;
                }

                if (sum > target) {
                    right--;
                } else if (sum < target) {
                    left++;
                } else {
                    return sum;
                }
            }
        }

        return res;
    }
}

[19] 删除链表的倒数第 N个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]
示例 2：
输入：head = [1], n = 1
输出：[]
示例 3：
输入：head = [1,2], n = 1
输出：[1]
提示：

链表中结点的数目为 sz

1 <= sz <= 30

0 <= Node.val <= 100

1 <= n <= sz

进阶：你能尝试使用一趟扫描实现吗？

解法一：

用栈来实现

先按照链表的顺序把所有的节点全部入栈

然后根据 n的数值，逐个节出栈，获取待删除节点和它的前一个结点

因为这里没办法特殊处理首元结点，所以可以引入头结点 dummy（也有称为哑节点的）

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        // 构造一个栈（LinedList是双向链表实现的栈）
        LinkedList<ListNode> list = new LinkedList<ListNode>();
        // 构造头结点，它的 next是首元结点
        ListNode dummy = new ListNode(0, head);
        
        // 从头结点开始，全部压入栈
        ListNode cur = dummy;
        while (cur != null) {
            list.add(cur);
            cur = cur.next;
        }

        // 逐个 poll出来，注意循环里面 poll的，都是不要的
        for (int i = 1; i < n; i++) {
            list.pollLast();
        }

        // poll出待处理的节点和前一个节点，并进行删除操作
        cur = list.pollLast();
        ListNode prev = list.pollLast();
        prev.next = cur.next;
        cur.next = null;
        // 返回首元结点
        return dummy.next;
    }
}

解法四：

双指针，可以实现一次遍历

定义快慢两个指针，首先快指针先行，拉开慢指针 n-1个身位，然后一起向后直到快指针到达最后一个结点。

此时慢指针恰好执行待删除的节点前一个节点

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        // 定义头结点，方便操作首元节点
        ListNode dummy = new ListNode();
        dummy.next = head;

        // 定义快慢指针
        ListNode fast = dummy, slow = dummy;

        for(int i = 0; i < n + 1; i++) {
            fast = fast.next;
        }

        while(fast != null) {
            fast = fast.next;
            slow = slow.next;
        }

        // 此时 slow定位到的是待删除节点的前一个节点
        ListNode tmp = slow.next;
        slow.next = tmp.next;
        // 便于垃圾回收
        tmp.next = null;

        return dummy.next;
    }
}

[24] 两两交换链表中的结点

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

进阶：你能在不修改链表节点值的情况下解决这个问题吗?（也就是说，仅修改节点本身。）

示例 1：
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：
输入：head = []
输出：[]

示例 3：
输入：head = [1]
输出：[1]

提示：
链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100

解法一：

递归

两两交换链表中的相邻结点，这个要求实际上和结点在链表中的具体的位置并没有关系。

所以可以使用递归，也就是说，我不管你是第几个节点，我只在意要把自己和下一个结点进行交换。

考虑到交换时，需要涉及到三个指针的操作：结点之间的爱情和双方家长的感受。而首元结点没有父亲，故需要创建头结点。

递归退出的条件：head == null(到最后了) || head.next == null(孤家寡人，没有对象)

class Solution {
    public ListNode swapPairs(ListNode head) {
        // 声明头结点
        ListNode dummy = new ListNode(0, head);

        // 第一个次调用时，head的前驱结点就是头结点
        ListNode prev = dummy;
        // 调用实际交换函数
        realSwap(head, prev);

        return dummy.next;
    }

    private void realSwap(ListNode head, ListNode prev) {
        // 递归退出条件
        if (head == null || head.next == null) {
            return;
        }

        // 另一个参与交换的节点
        ListNode p = head.next;

        // 进行交换
        prev.next = p;
        head.next = p.next;
        p.next = head;

        // 在下一次递归时，第一个结点的前驱结点
        prev = head;
        // 递归调用
        realSwap(head.next, prev);
    }
}

[33] 搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4
示例 2：
输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1
示例 3：
输入：nums = [1], target = 0
输出：-1
提示：

1 <= nums.length <= 5000

-104 <= nums[i] <= 104

nums 中的每个值都 独一无二

题目数据保证 nums 在预先未知的某个下标上进行了旋转

-104 <= target <= 104

Related Topics

数组

二分查找

解法一：

二分查找

但是要明确当前 mid 在哪里，是在左边呢，还是右边，记得画个图

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        
        while(left <= right) {
            int mid = left + (right - left) / 2;
            
            if (nums[mid] == target) {
                return mid;
                // 说明 mid 在右边
            } else if (nums[mid] < nums[right]) {
                // 说明 target在 mid 和 right之间
                if (nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            } else {
                // 此时 mid 可能在右边，也可能在 左边
                // 但能明确的是 target 在 left 和 mid 之间
                if (target >= nums[left] && target < nums[mid]) {
                    right = mid - 1;
                } else {
                    left = mid + 1;
                }
            }
        }

        return -1;
    }
}

[36] 有效的数独

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

提示：

board.length == 9
board[i].length == 9
board[i][j] 是一位数字（1-9）或者 '.'

Related Topics

数组

哈希表

矩阵

解法一：

遍历每一行，遍历每一列，遍历每一个 3x3 的大格子，判断是否存在重复

class Solution {
    public boolean isValidSudoku(char[][] board) {
        int len = board.length;
        // 行
        int[][] line = new int[len][len];
        // 列
        int[][] column = new int[len][len];
        // 大格子
        int[][] cell = new int[len][len];

        for (int i = 0; i < len; i++) {
            for (int j = 0; j < len; j++) {
                // 这一格没有数据，就跳过
                if (board[i][j] == '.') {
                    continue;
                }
                // 获取当前小格子里的数字，board[i][j]最小是 '1'，'1'-'0' = 1，但是数组的最小下标为 0，所以再减一
                int smallCur = board[i][j] - '0' - 1;
                // 判断当前小格子在哪个大格子内（重点）
                int bigCur = i / 3 * 3 + j / 3;
                // 小格子里面的数字曾经出现过了，说明有重复，就返回 false
                if (line[i][smallCur] != 0 || column[j][smallCur] != 0 || cell[bigCur][smallCur] != 0) {
                    return false;
                }
                // 否则就存下该数字
                line[i][smallCur] = column[j][smallCur] = cell[bigCur][smallCur] = 1;
            }
        }

        return true;
    }
}

[38] 外观数列

你可以将其视作是由递归公式定义的数字字符串序列：

countAndSay(1) = "1"
countAndSay(n) 是对 countAndSay(n-1) 的描述，然后转换成另一个数字字符串。

前五项如下：

1.     1
2.     11
3.     21
4.     1211
5.     111221
第一项是数字 1 
描述前一项，这个数是 1 即 “ 一 个 1 ”，记作 "11"
描述前一项，这个数是 11 即 “ 二 个 1 ” ，记作 "21"
描述前一项，这个数是 21 即 “ 一 个 2 + 一 个 1 ” ，记作 "1211"
描述前一项，这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ，记作 "111221"

要描述一个数字字符串，首先要将字符串分割为最小数量的组，每个组都由连续的最多 相同字符 组成。然后对于每个组，先描述字符的数量，然后描述字符，形成一个描述组。要将描述转换为数字字符串，先将每组中的字符数量用数字替换，再将所有描述组连接起来。

例如，数字字符串 "3322251" 的描述如下图：

示例 1：

输入：n = 1
输出："1"
解释：这是一个基本样例。

示例 2：

输入：n = 4
输出："1211"
解释：
countAndSay(1) = "1"
countAndSay(2) = 读 "1" = 一 个 1 = "11"
countAndSay(3) = 读 "11" = 二 个 1 = "21"
countAndSay(4) = 读 "21" = 一 个 2 + 一 个 1 = "12" + "11" = "1211"

提示：

1 <= n <= 30

Related Topics

字符串

解法一：

递归

每一次处理前先获取上一次的结果 res，针对上一次的结果进行操作。

如果 n==1，那么就返回 “1”

具体处理时，遍历 res，针对直接重复的元素进行统计

class Solution {
    public String countAndSay(int n) {
        // 递归退出条件
        if (n == 1) {
            return "1";
        }


        char[] arr = countAndSay(n - 1).toCharArray();
        // 记录本次处理的结果
        StringBuffer sb = new StringBuffer();
        int count = 1;

        // 遍历上一次的结果
        for (int i = 0; i < arr.length - 1; i++) {
            // 如果相同，则叠加次数
            if (arr[i] == arr[i + 1]) {
                count++;
                continue;
            } 
            // 否则就将次数和当前字符记录到结果中
            sb.append(count);
            sb.append(arr[i]);
            // 重置统计次数
            count = 1;

        }

        // 注意跳出循环时，最后一个字符可能会不统计
        sb.append(count);
        sb.append(arr[arr.length - 1]);

        // 返回结果
        return sb.toString();
    }
}

[39] 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。
示例 2：
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3：
输入: candidates = [2], target = 1
输出: []
提示：

1 <= candidates.length <= 30

1 <= candidates[i] <= 200

candidate 中的每个元素都 互不相同

1 <= target <= 500

Related Topics

数组

回溯

解法一：

回溯

注意：一般需要两个集合，并且具体的加和减都是放到循环里面的

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
       traverse(candidates, 0, target);
       return res; 
    }

    private void traverse(int[] candidates, int idx, int target) {
        if (target < 0) {
            return;
        } else if (target == 0) {
            res.add(new ArrayList<Integer>(path));
            return;
        } 

        // 从 idx 开始遍历，能减枝并且保证顺序
        for(int i = idx; i < candidates.length; i++) {
            path.add(candidates[i]);
            traverse(candidates, i, target - candidates[i]);
            path.remove(path.size() - 1);
        }
    }
}

[40] 组合总和Ⅱ

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
提示:

1 <= candidates.length <= 100

1 <= candidates[i] <= 50

1 <= target <= 30

Related Topics

数组

回溯

解法一：

回溯

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);

        traverse(candidates, target, 0);
        return res;
    }

    private void traverse(int[] candidates, int target, int idx) {
        if (target < 0) {
            return;
        } if (target == 0) {
            res.add(new ArrayList<Integer>(path));
        }

        for(int i = idx; i < candidates.length; i++) {
            // 剪枝，保证不重复
            if (i > idx && candidates[i] == candidates[i-1]) {
                continue;
            }
            
            path.add(candidates[i]);
            traverse(candidates, target - candidates[i], i + 1);
            path.remove(path.size() - 1);
        }
    }
}

[45] 跳跃游戏Ⅱ

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

假设你总是可以到达数组的最后一个位置。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
  从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示:

1 <= nums.length <= 104
0 <= nums[i] <= 1000

Related Topics

贪心

数组

动态规划

解法一：

贪心

class Solution {
    public int jump(int[] nums) {
        // 目前能跳到的最远距离，上次跳跃的最远距离，跳跃次数
        int far = 0, end = 0, res = 0;

        for(int i = 0; i < nums.length - 1; i++) {
            far = Math.max(far, i + nums[i]); // 更新最远距离
            if (i == end) { // 如果抵达了上次能跳到的最远距离，那么就更新下一跳的最远距离
                end = far;
                res++;
            }
        }
        return res;
        
    }
}

[46] 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：
输入：nums = [1]
输出：[[1]]
提示：

1 <= nums.length <= 6

-10 <= nums[i] <= 10

nums 中的所有整数 互不相同

Related Topics

数组

回溯

解法一：

遍历决策树，回溯算法

详见 day17: 回溯算法原理

class Solution {

    // 定义结果列表，保存每个路径
    List<List<Integer>> res = new LinkedList<>();


    public List<List<Integer>> permute(int[] nums) {
        // 定义当前路径列表
        LinkedList<Integer> track = new LinkedList<>();
        // 决策树向下递归
        backtrack(nums, track);
        return res;
    }

    /**
     * 路径：记录在 track中
     * 选择列表：nums中不存在于 track的那些元素
     * 结束条件：nums中的元素全都在 track中出现
     *
     * @param nums
     * @param track
     */
    private void backtrack(int[] nums, LinkedList<Integer> track) {
        // 如果当前路径的长度等于数组的长度，也就是说，决策树递归到叶子节点了
        if (track.size() == nums.length) {
            // 就把当前的路径添加到结果列表中
            res.add(new LinkedList<>(track));
            return;
        }

        // 遍历整个数组
        for (int i = 0; i < nums.length; i++) {
            // 如果取到的值已经在路径中出现过了，就跳过这个数
            if (track.contains(nums[i])) {
                continue;
            }

            // 将这个数添加到路径列表中，即访问决策树中的这个节点
            track.add(nums[i]);

            // 进入下一层决策树
            backtrack(nums, track);

            // 取消选择，回退一层
            track.removeLast();
        }
    }
}

解法二：

优化解法，不使用 contains()判断，而是将原数组划分成左右两个部分，左边表示已经填过了的数，右边表示待填的数，动态维护这个数组。

具体来说，假设我们已经填到第 first 个位置，那么 nums 数组中 [0,first−1] 是已填过的数的集合，[first,n−1] 是待填的数的集合。我们肯定是尝试用 [first,n−1] 里的数去填第 first 个数，假设待填的数的下标为 i ，那么填完以后我们将第 i 个数和第 first 个数交换，即能使得在填第 first+1个数的时候 nums 数组的[0,firs**t] 部分为已填过的数，[first+1,n−1] 为待填的数，回溯的时候交换回来即能完成撤销操作。

class Solution { 
    public List<List<Integer>> permute(int[] nums) { 
        List<List<Integer>> res = new ArrayList<>(); 
        List<Integer> output = new ArrayList<>(); 
        
        for (int num : nums) { 
            output.add(num); 
        } 
        
        int n = nums.length; 
        backtrack(n, output, res, 0); 
        return res; 
    } 
    
    public void backtrack(int n, List<Integer> output, List<List<Integer>> res, int first) { 
        // 所有数都填完了
        if (first == n) { 
            res.add(new ArrayList<Integer>(output)); 
        } 
        
        for (int i = first; i < n; i++) { 
            // 动态维护数组 
            Collections.swap(output, first, i); 
            // 继续递归填下一个数 
            backtrack(n, output, res, first + 1); 
            // 撤销操作 
            Collections.swap(output, first, i); 
        } 
    } 
}

第二次手写

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> curVal = new ArrayList<>();
    // 之所以需要 visited数组是因为每次回溯的时候都需要从 0 ~ len遍历，必须记录哪几个已经遍历过了
    boolean[] visited;

    public List<List<Integer>> permute(int[] nums) {
        visited = new boolean[nums.length];
        traverse(nums, 0);
        return res;
    }

    private void traverse(int[] nums, int idx) {
        if (idx == nums.length) {
            res.add(new ArrayList<>(curVal));
            return;
        }

        for(int i = 0; i < nums.length; i++) {
            if (visited[i]) {
                continue;
            }
            
            curVal.add(nums[i]);
            visited[i] = true;

            traverse(nums, idx+1);
            
            curVal.remove(curVal.size() - 1);
            visited[i] = false;
        }

    }
}

[47] 全排列Ⅱ

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：
输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示：

1 <= nums.length <= 8

-10 <= nums[i] <= 10

Related Topics

数组

回溯

解法一：

DFS

需要注意的是，甄别重复数字，因此原来的 contains()判断，需要改用标志数组。

class Solution {

    List<List<Integer>> res = new LinkedList<>();
    boolean[] vis;

    public List<List<Integer>> permuteUnique(int[] nums) {

        vis = new boolean[nums.length];

        // 定义当前路径列表
        LinkedList<Integer> track = new LinkedList<>();
        Arrays.sort(nums);
        // 决策树向下递归
        backtrack(nums, track);
        return res;
    }

    public void backtrack(int[] nums, LinkedList<Integer> track) {
        // 如果当前路径的长度等于数组的长度，也就是说，决策树递归到叶子节点了
        // System.out.println(track.size() + "   " + nums.length);
        if (track.size() == nums.length) {
            // 就把当前的路径添加到结果列表中
            res.add(new LinkedList<>(track));
            return;
        }

        // 遍历整个数组
        for (int i = 0; i < nums.length; i++) {
            // 因为可能存在重复的数字，所以不能简单的用 contains进行判断，不然的话，重复的数都会被 continue跳过
            /*if (track.contains(nums[i])) {
                continue;
            }*/

            /*
            vis[i]: 表示已经遍历过了第 i个数
            i > 0: 方便之后对 数组[i-1]值的获取
            nums[i] == nums[i-1]: 当前遍历的是重复的那个数字
            !vis[i-1]: 限制相邻节点的访问顺序
             */
            if (vis[i] 
                    || (i > 0 
                            && nums[i] == nums[i - 1] 
                            && !vis[i - 1])) {
                continue;
            }

            // 将这个数添加到路径列表中，即访问决策树中的这个节点
            track.add(nums[i]);
            // 设置当前节点已被访问
            vis[i] = true;

            // 进入下一层决策树
            backtrack(nums, track);

            // 后撤时，清楚访问标志
            vis[i] = false;

            // 取消选择，回退一层
            track.removeLast();
        }
    }
}

第二次手写：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    boolean[] visited;

    public List<List<Integer>> permuteUnique(int[] nums) {
        visited = new boolean[nums.length];
        Arrays.sort(nums);
        traverse(nums);
        return res;
    }

    private void traverse(int[] nums) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<Integer>(path));
            return;
        }

        for(int i = 0; i < nums.length; i++) {
            if (visited[i]) {
                continue;
            } else if (i > 0 && nums[i] == nums[i-1] && visited[i-1]) {
                continue;
            }

            path.add(nums[i]);
            visited[i] = true;

            traverse(nums);

            visited[i] = false;
            path.remove(path.size() - 1);
        }
    }
}

[48] 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
示例 2：
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3：
输入：matrix = [[1]]
输出：[[1]]
示例 4：
输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]
提示：

matrix.length == n

matrix[i].length == n

1 <= n <= 20

-1000 <= matrix[i][j] <= 1000

Related Topics

数组

数学

矩阵

解法一：

使用 LinkedList暂存数据，然后对数组内原有的数据进行覆盖

class Solution {
    public void rotate(int[][] matrix) {
        if (matrix.length <= 1) {
            return;
        }

        // 先存起来
        LinkedList<Integer> list = new LinkedList<>();
        for (int[] ints : matrix) {
            for (int anInt : ints) {
                list.add(anInt);
            }
        }

        // 再写出去
        for (int i = matrix.length - 1; i >= 0; i--) {
            for (int j = 0; j < matrix.length; j++) {
                matrix[j][i] = list.pop();
            }
        }

    }
}

解法二：

先水平反转，再对角线反转

因为是对角线反转，所以可以只遍历上半区或者下半区即可

关键在于找到交换的式子

class Solution {
    public void rotate(int[][] matrix) {
        if (matrix.length <= 1) {
            return;
        }
        
        // 水平反转
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix.length / 2; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[i][matrix.length - j - 1];
                matrix[i][matrix.length - j - 1] = tmp;
            }
        }

        
        // 对角线反转
        for (int i = 0; i < matrix.length; i++) {
            for (int j = matrix.length -i - 1; j < matrix.length; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[matrix.length - j - 1][matrix.length - i - 1];
                matrix[matrix.length - j - 1][matrix.length - i - 1] = tmp;

            }
        }
    }
}

[49] 字母异位词分组

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的字母得到的一个新单词，所有源单词中的字母通常恰好只用一次。

示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示：

1 <= strs.length <= 104

0 <= strs[i].length <= 100

strs[i] 仅包含小写字母

Related Topics

数组

哈希表

字符串

排序

解法一：

朴素解法

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        List<List<String>> res = new ArrayList<>();
        if (strs == null || strs.length == 0) {
            return res;
        }
        // 按照字符串的长度排序
        Arrays.sort(strs, (o1, o2) -> o1.length() - o2.length());
        
        Map<Character, Integer> char_freq = new HashMap<>();
        Map<Character, Integer> inner_char = new HashMap<>();
        List<String> same = new ArrayList<>();
        boolean[] visited = new boolean[strs.length];
        int idx = 0;

        while(idx < strs.length) {
            same.clear();
            char_freq.clear();

            String cur = strs[idx];
            if (visited[idx]) {
                idx++;
                continue;
            }

            // 记录当前字符串中各字符的出现频率
            for(char x : cur.toCharArray()) {
                char_freq.put(x, char_freq.getOrDefault(x, 0) + 1);
            }
            same.add(cur);
            visited[idx] = true;


            // 像后找同频率的字符串
            int i = idx + 1;
            while(i < strs.length && strs[i].length() == cur.length()) {
                if (visited[i]) {
                    i++;
                    continue;
                }

                inner_char.clear();
                for(char x : strs[i].toCharArray()) {
                    inner_char.put(x, inner_char.getOrDefault(x, 0) + 1);
                }
                
                if (inner_char.size() != char_freq.size()) {
                    i++;
                    continue;
                }
                
                int valid = 0;
                for(char x : inner_char.keySet()) {
                    if (!char_freq.containsKey(x)) {
                        break;                        
                    }
                    if (!char_freq.get(x).equals(inner_char.get(x))) {
                        break;
                    } 

                    valid++;       
                }
                
                if (valid == char_freq.size()) {
                    same.add(strs[i]);
                    visited[i] = true;
                }
                i++;
            }

            res.add(new ArrayList<String>(same));
            idx++;
        }

        return res;
    }
}

解法二：

对字符串中的字符排序，便于判断是否存在同位词

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> map = new HashMap<>();
        
        for(String x : strs) {
            char[] tmp = x.toCharArray();
            Arrays.sort(tmp);
            String key = new String(tmp);
            if (!map.containsKey(key)) {
                map.put(key, new ArrayList<String>());
            }
           map.get(key).add(x);
        }
        return new ArrayList<>(map.values());

    }
}

[53] 最大子数组和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：
输入：nums = [1]
输出：1
示例 3：
输入：nums = [0]
输出：0
示例 4：
输入：nums = [-1]
输出：-1
示例 5：
输入：nums = [-100000]
输出：-100000
提示：

1 <= nums.length <= 105

-104 <= nums[i] <= 104

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

Related Topics

数组

分治

动态规划

解法一：

建立数组 int[] dp，dp[i]表示从 nums[0] 到 nums[i]中的最长连续子序和

迭代关系为：

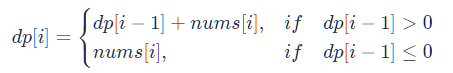
class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 1) {
            return nums[0];
        }

        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int res = dp[0];
        for (int i = 1; i < dp.length; i++) {
            if (dp[i - 1] < 0) {
                dp[i] = nums[i];
            } else {
                dp[i] = nums[i] + dp[i - 1];
            }

            res = Math.max(res, dp[i]);
        }

        return res;
    }
}

[54] 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]
示例 2：
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]
提示：

m == matrix.length

n == matrix[i].length

1 <= m, n <= 10

-100 <= matrix[i][j] <= 100

Related Topics

数组

矩阵

模拟

解法一：

每一次循环都进行一次：→↓←↑的遍历

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length; // 宽
        int n = matrix[0].length; // 长
        
        int upper = 0, lower = m - 1;
        int left = 0, right = n - 1;
        List<Integer> res = new ArrayList<>(m * n);
        
        while (res.size() < m * n) {
            // 注意这些 if判断
            if (upper <= lower) {
                for (int i = left; i <= right; i++) {
                    res.add(matrix[upper][i]);
                }
                upper++;
            }

            if (left <= right) {
                for (int i = upper; i <= lower; i++) {
                    res.add(matrix[i][right]);
                }
                right--;
            }

            if (upper <= lower) {
                for (int i = right; i >= left; i--) {
                    res.add(matrix[lower][i]);
                }
                lower--;
            }
            if (left <= right) {
                for (int i = lower; i >= upper; i--) {
                    res.add(matrix[i][left]);
                }
                left++;
            }
        }
        return res;
    }
}

第二次刷的时候手写

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int left = 0, right = matrix[0].length - 1, top = 0, botton = matrix.length - 1;
        List<Integer> res = new ArrayList<Integer>();

        while(res.size() < matrix.length * matrix[0].length) {
            // 注意等号的判断
            if (top <= botton) {
                for(int i = left; i <= right; i++) {
                    res.add(matrix[top][i]);
                }
                top++;
            }

            if (left <= right) {
                for(int i = top; i <= botton; i++) {
                    res.add(matrix[i][right]);
                }
                right--;
            }

            if (top <= botton) {
                for(int i = right; i >= left; i--) {
                    res.add(matrix[botton][i]);
                }
                botton--;
            }

            if(left <= right) {
                for(int i = botton; i >= top; i--) {
                    res.add(matrix[i][left]);
                }
                left++;
            }
        }

        return res;

    }
}

[55] 跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

提示：

1 <= nums.length <= 3 * 104
0 <= nums[i] <= 105

Related Topics

贪心

数组

动态规划

解法一：

贪心

class Solution {
    public boolean canJump(int[] nums) {
        int far = 0;
        for(int i = 0; i < nums.length; i++) {
            // 如果连第 i个都跳不到，更不用说后面的了
            if (far < i) {
                return false;
            }
            // 更新能跳到最远的距离
            far = Math.max(far, i + nums[i]);
        }

        return true;
    }
}

[56] 合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：
输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2：
输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示：

1 <= intervals.length <= 104

intervals[i].length == 2

0 <= starti <= endi <= 104

Related Topics

数组

排序

解法一：

先对区间按左边排序，然后判断是否存在重叠

否，加入到结果集中
是，扩大区间

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (o1, o2) -> o1[0]-o2[0]);

        int idx = 0;
        int left = -1, right = -1;

        List<int[]> res = new ArrayList<>();

        while(idx < intervals.length) {
            left = left == -1 ? intervals[idx][0] : left;
            right = right == -1 ? intervals[idx][1] : right;

            // 判断是否存在区间重叠
            if (idx + 1 < intervals.length && right >= intervals[idx + 1][0]) {
                right = Math.max(right, intervals[idx + 1][1]);
            } else {
                res.add(new int[]{left, right});
                left = -1;
                right = -1;
            }

            idx++;
        }
        
        return res.toArray(new int[0][0]);
    }
}

[59] 螺旋矩阵Ⅱ

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
示例 2：
输入：n = 1
输出：[[1]]
提示：

1 <= n <= 20

Related Topics

数组

矩阵

模拟

解法一：

基本同遍历

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] matrix = new int[n][n];
        int top = 0, bottom = n - 1;
        int left = 0, right = n - 1;
        int num = 1;
		// 注意 <=
        while (num <= n * n) {
            if (top <= bottom) {
                for (int i = left; i <= right; i++) {
                    matrix[top][i] = num++;
                }
                top++;
            }

            if (left <= right) {
                for (int i = top; i <= bottom; i++) {
                    matrix[i][right] = num++;
                }
                right--;
            }

            if (top <= bottom) {
                for (int i = right; i >= left; i--) {
                    matrix[bottom][i] = num++;
                }
                bottom--;
            }

            if (left <= right) {
                for (int i = bottom; i >= top; i--) {
                    matrix[i][left] = num++;
                }
                left++;
            }
        }
        return matrix;
    }
}

[61] 旋转链表

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]

示例 2：

输入：head = [0,1,2], k = 4
输出：[2,0,1]

提示：

链表中节点的数目在范围 [0, 500] 内
-100 <= Node.val <= 100
0 <= k <= 2 * 109

解法一：

仔细看题目，从数学的角度来思考，每个结点都后移 k个位置，那么肯定存在某一部分的顺序不变的情况。

画个草图思考一下：

所以，可以这么认为：实际上就是把最后的几个节点拎到了前面

考虑到示例二，k的数值可能大于结点数，所以计算公式如下：前移的节点个数 = k % 结点的总数

class Solution {
    public ListNode rotateRight(ListNode head, int k) {
        if (head == null || head.next == null || k == 0) {
            return head;
        }

        // 主要操作的就是 p结点
        ListNode p = head;

        // 统计总的结点个数
        int nodeNum = 0;
        while (p != null) {
            p = p.next;
            nodeNum++;
        }

        // 实际要迁移的节点个数
        int realMoved = k % nodeNum;
        // 有可能 一共 5各节点，然后 k = 5，那么就都不用动
        if (realMoved == 0) {
            return head;
        }

        // 定位到第一个待移动结点的前面那个结点，也就是示例一中的 3的位置，
        p = head;
        for (int i = 0; i < nodeNum - realMoved - 1; i++) {
            p = p.next;
        }

        // 获取第一个需要移动的结点，在最后，它就会变成链表的新的首元结点
        ListNode q = p.next;
        // 而第一个需要移动的结点的前驱结点，就会变成链表的新的最后一个结点
        p.next = null;
        p = q;

        // 定位到最后一个结点
        while (p.next != null) {
            p = p.next;
        }

        // 最后一个结点指向头结点
        p.next = head;
        return q;
    }
}

自己写的解法第一次有这么好的效果

解法二：

针对解法一进行优化，可以减少一次结点的遍历

在第一次遍历统计结点的个数结束后，就让最后一个结点指向首元结点，形成一个环。

最后在通过遍历，进行实际移动的节点的定位时，再把环打开，这就减少了第三次的遍历过程

class Solution {
    public ListNode rotateRight(ListNode head, int k) {
        if (head == null || head.next == null || k == 0) {
            return head;
        }

        ListNode p = head;

        int nodeNum = 0;
        while (p.next != null) {
            p = p.next;
            nodeNum++;
        }
        nodeNum++;


        int realMoved = k % nodeNum;
        if (realMoved == 0) {
            return head;
        }
		// 成环
        p.next = head;
        p = head;
        for (int i = 0; i < nodeNum - realMoved - 1; i++) {
            p = p.next;
        }
		// 更改首元结点
        head = p.next;
        // 打断
        p.next = null;
        return head;
    }
}

[62] 不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：
输入：m = 3, n = 7
输出：28
示例 2：
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3：
输入：m = 7, n = 3
输出：28
示例 4：
输入：m = 3, n = 3
输出：6
提示：

1 <= m, n <= 100

题目数据保证答案小于等于 2 * 109

Related Topics

数学

动态规划

组合数学

解法一：

动态规划

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for(int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }

        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        
        return dp[m - 1][n - 1];
    }
}

[64] 最小路径和

给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
示例 2：
输入：grid = [[1,2,3],[4,5,6]]
输出：12
提示：

m == grid.length

n == grid[i].length

1 <= m, n <= 200

0 <= grid[i][j] <= 100

Related Topics

数组

动态规划

矩阵

解法一：

基本题

class Solution {
    public int minPathSum(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;

        int[][] dp = new int[row][col];
        dp[0][0] = grid[0][0];

        // 先初始化基本的行和列
        for (int i = 1; i < row; i++) {
            dp[i][0] = grid[i][0] + dp[i - 1][0];
        }

        for (int i = 1; i < col; i++) {
            dp[0][i] = grid[0][i] + dp[0][i - 1];
        }

        // 某一格的值就是上下两格的最小值加当前格的基本值
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }

        return dp[row - 1][col - 1];
    }
}

[75] 颜色分类

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库的sort函数的情况下解决这个问题。

示例 1：
输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]
示例 2：
输入：nums = [2,0,1]
输出：[0,1,2]
提示：

n == nums.length

1 <= n <= 300

nums[i] 为 0、1 或 2

进阶：

你可以不使用代码库中的排序函数来解决这道题吗？

你能想出一个仅使用常数空间的一趟扫描算法吗？

Related Topics

数组

双指针

排序

解法一：

头尾双指针，遇到 0 就通过交换放到头上，遇到 2 就通过交换放到尾巴；

注意交换 2 的时候可能得到 0，也可能再得到 2；

class Solution {
    public void sortColors(int[] nums) {
        int left = 0, right = nums.length - 1;
        int i = 0;
        while(i <= right) {
            int cur = nums[i];
            if (cur == 0) {
                // 而这里不同担心，因为 i 本来就是从左边过来的
                swap(nums, left, i);
                left++;
                i++;
            } else if (cur == 1) {
                i++;
            } else if (cur == 2) {
                // 当 cur == 2 的时候，cur 会和 nums[right]交换位置
                // 此时交换得到的值可能是 0 或 2，因此不能立刻 i++
                swap(nums, right, i);
                right--;
            }
            
        }
    }

    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

[77] 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：
输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2：
输入：n = 1, k = 1
输出：[[1]]
提示：

1 <= n <= 20

1 <= k <= n

Related Topics

回溯

解法一：

回溯

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        traverse(n, k, 0);
        return res;
    }

    private void traverse(int n, int k, int idx) {
        if (path.size() == k) {
            res.add(new ArrayList<Integer>(path));
            return;
        }

        // 这里其实还可以进行剪枝，i < n 可以细化为 i < n - (k - path.size()) + 1
        for(int i = idx; i < n; i++) {
            path.add(i + 1);
            traverse(n, k, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

[78] 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2：
输入：nums = [0]
输出：[[],[0]]
提示：

1 <= nums.length <= 10

-10 <= nums[i] <= 10

nums 中的所有元素 互不相同

Related Topics

位运算

数组

回溯

解法一：

回溯

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        traverse(nums, 0);
        return res;
    }

    private void traverse(int[] nums, int idx) {
        res.add(new ArrayList<>(path));
        // 从 idx 开始遍历，保证 path中的元素有序
        for(int i = idx; i < nums.length; i++) {
            path.add(nums[i]);
            traverse(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

[80] 删除有序数组中的重复项Ⅱ

给你一个有序数组 nums ，请你原地删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

说明：

为什么返回数值是整数，但输出的答案是数组呢？

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。 不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,1,2,3,3]
输出：7, nums = [0,0,1,1,2,3,3]
解释：函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3 。 不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列

Related Topics

数组

双指针

解法一：

双指针，解题模板

class Solution {
    public int removeDuplicates(int[] nums) {
        // 出现多少次，就传多少
        return process(nums, 2);
    }

    private int process(int[] nums, int cnt) {
        int idx = 0;
        for (int x : nums) {
            // 其实本质就是和前几位进行比较
            if (idx < cnt || nums[idx - cnt] != x) {
                nums[idx++] = x;
            }
        }

        return idx;
    }
}

[82] 删除排序链表中的重复元素Ⅱ

存在一个按升序排列的链表，给你这个链表的头节点 head

请你删除链表中所有存在数字重复情况的节点，只保留原始链表中没有重复出现的数字。

返回同样按升序排列的结果链表。

示例 1：

输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

示例 2：

输入：head = [1,1,1,2,3]
输出：[2,3]

提示：

链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序排列

解法一：

三指针，prev, cur, nxt。

当 cur.val == nxt.val时，使 nxt一直向后迭代直到nxt.val != cur.val，最后另 prev.next = nxt

否则就正常地逐个迭代

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null) {
            return head;
        }
        ListNode dummy = new ListNode(- 1, head);
        ListNode prev = dummy, cur = head, nxt = head.next;
        // 为了保证像 111111这种能够显示为 []，需要设置一个标志位
        boolean flag = false;

        while (nxt != null) {
            if (nxt.val == cur.val) {
                nxt = nxt.next;
                // 设置标志位
                flag = true;
                continue;
            }

            // 如果标志为 true，表示需要设置 prev.next = nxt
            if (flag) {
                prev.next = nxt;
                cur = nxt;
                nxt = nxt.next;
                // 设置标志位
                flag = false;
                // 否则每个指针都正常向后迭代以为
            } else {
                prev = cur;
                cur = nxt;
                nxt = nxt.next;
            }
        }

        // 为了保证即使链表的最后节点重复也能够去重，需要再判断一次
        if (flag) {
            prev.next = nxt;
        }

        return dummy.next;
    }
}

解法二：

先判断后两位是否重复，若重复，则一直去重

class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        ListNode dummy = new ListNode(-1);
        ListNode cur = dummy;

        while (head != null) {
            // 注意，这里要先判断添加，再去重
            // 否则会剩下一个重复的，且无法再直接知道它是不是重复的了 -> 1111 变成了 1，然后也不知道 1是不是重复的
            if (head.next == null || head.val != head.next.val) {
                cur.next = head;
                cur = head;
            }

            while (head.next != null && head.val == head.next.val) {
                head = head.next;
            }
            
            head = head.next;
        }

        cur.next = null;
        return dummy.next;
    }
}

[90] 子集Ⅱ

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2：
输入：nums = [0]
输出：[[],[0]]
提示：

1 <= nums.length <= 10

-10 <= nums[i] <= 10

Related Topics

位运算

数组

回溯

解法一：

回溯

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        traverse(nums, 0);
        return res;
    }

    private void traverse(int[] nums, int idx) {
        
        res.add(new ArrayList<>(path));

        for(int i = idx; i < nums.length; i++) {
            // 如果存在重复的，就剪枝，注意这个 i > idx 的条件，别减多了
            if (i > idx && nums[i] == nums[i-1]) {
                continue;
            }

            path.add(nums[i]);
            traverse(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

[92] 反转链表Ⅱ

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。

请你反转从位置 left 到位置 right 的链表节点，返回反转后的链表。

示例 1：
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

示例 2：
输入：head = [5], left = 1, right = 1
输出：[5]

提示：
链表中节点数目为 n
1 <= n <= 500
-500 <= Node.val <= 500
1 <= left <= right <= n

解法一：

传统的方法，先定位到反转开始的位置，然后通过三个节点实现反转

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if(head == null || left == right) {
            return head;
        }

        // 定义头结点
        ListNode dummy = new ListNode(-1);
        dummy.next = head;

        // 定位到 left前一个节点
        ListNode slow = dummy;
        for(int i = 1; i < left; i++) {
            slow = slow.next;
        }

		// begin记录头
        ListNode begin = slow, fast = slow.next.next;
        slow = slow.next;
        // 避免在逆转的开始成环
        slow.next = null;

        int cnt = left;
        while(cnt < right) {
            ListNode tmp = fast.next;
            fast.next = slow;
            slow = fast;
            fast = tmp;
            cnt++;
        }
		// begin.next是曾经的头，而此时的 fast就是 end
        begin.next.next = fast;
        begin.next = slow;
        
        return dummy.next;
    }
}

解法二：

递归反转

class Solution {
    // 搞个类变量，到时候记录 逆序部分之后的直接连接的节点
    ListNode successor = null;
    
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if (left == right || head == null) {
            return head;
        }

        return traverse(head, left, right);
    }

    private ListNode traverse(ListNode head, int left, int right) {
        
        // 此时左边已经放完了
        if (left == 1) {
            // 当 right==1的时候，说明已经达到需要逆转的最右边了，此时记录 successor，并直接返回 head
            if (right == 1) {
                successor = head.next;
                return head;
            }

            ListNode tail = traverse(head.next, left, right - 1);
            head.next.next = head;
            // 这里设置 head.next = successor
            // 也就是说针对右边的那些节点，他们的 next指针会变化两次，先指向 successor，在当前递归出来之后再指向 head
            // 而针对最左边的节点，也就是即将退出所有递归时的节点，它只会设置一次，刚好就是 successor
            head.next = successor;

            return tail;
        } 
        
        // 先把左边放过来
        head.next = traverse(head.next, left - 1 , right - 1);
        return head;
        
    }
}

[95] 不同的二叉搜索树Ⅱ

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2：
输入：n = 1
输出：[[1]]
提示：

1 <= n <= 8

Related Topics

树

二叉搜索树

动态规划

回溯

二叉树

解法一：

基本逻辑类似于第 96题

class Solution {
    public List<TreeNode> generateTrees(int n) {
        if (n == 0) {
            return new ArrayList<>();
        }
        return build(1, n);
    }


    private List<TreeNode> build(int left, int right) {
        List<TreeNode> res = new ArrayList<>();
        // base condition
        if (left > right) {
            res.add(null);
            return res;
        }

		// recurse
        for (int i = left; i <= right; i++) {
            List<TreeNode> leftList = build(left, i - 1);
            List<TreeNode> rightList = build(i + 1, right);
			// construct
            for (TreeNode lNode : leftList) {
                for (TreeNode rNode : rightList) {
                    TreeNode root = new TreeNode(i);
                    root.left = lNode;
                    root.right = rNode;
                    // get in collection
                    res.add(root);
                }
            }

        }

        return res;
    }
}

[96] ❤ 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：
输入：n = 3
输出：5
示例 2：
输入：n = 1
输出：1
提示：

1 <= n <= 19

Related Topics

树

二叉搜索树

数学

动态规划

二叉树

解法一：

n个节点中组成的 BST的数量为 (左子树的可能数量 * 右子树的可能数量)，而单个子树中节点的数量为从 1到 n不等

其实我觉得这并不算 dp，而是建了一个缓存罢了；换成 HashMap来存也是一样的

class Solution {
    int[][] dp;

    public int numTrees(int n) {
        dp = new int[n + 1][n + 1];
        return count(1, n);
    }

    private int count(int left, int right) {
        if (left > right) {
            return 1;
        }

        if (dp[left][right] != 0) {
            return dp[left][right];
        }

        int res = 0;
        for (int i = left; i <= right; i++) {
            int lValue = count(left, i - 1);
            int rValue = count(i + 1, right);
            res += lValue * rValue;
        }
        dp[left][right] = res;

        return res;
    }
}

优化，推导 dp[i]和 dp[i-1]等之间的算术关系

假设 n 个节点存在二叉排序树的个数是 G (n)，令 f(i) 为以 i 为根的二叉搜索树的个数
- G(n) = f(1, n) + f(2, n) + f(3, n) + f(4, n) + ... + f(n, n)
当 i 为根节点时，其左子树节点个数为 i-1 个，右子树节点为 n-i
- f(i) =G (i−1) ∗ G(n−i)
综合以上两个公式，可得
- G(n) = G(0) ∗ G(n−1) + G(1) ∗ (n−2) + ... + G(n−1) ∗ G(0)

由此可得：

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
		// 双重 for 循环，构成乘式的累加和
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= i - 1; j++) {
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }

        return dp[n];
    }
}

[102] 二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。（即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7],
 3
/ \\
9  20
 /  \\
15   7
返回其层序遍历结果：
[
[3],
[9,20],
[15,7]
]
Related Topics

树

广度优先搜索

二叉树

解法一：

BFS

即层序遍历

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {

        Queue<TreeNode> queue = new LinkedList<>();
        ArrayList<List<Integer>> out = new ArrayList<>();

        if (root == null) {
            return out;
        }
        
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            ArrayList<Integer> in = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                in.add(cur.val);

                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            out.add(in);
        }
        return out;
    }
}

[105] 从前序与中序遍历序列构造二叉树

给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。

示例 1:
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
提示:

1 <= preorder.length <= 3000

inorder.length == preorder.length

-3000 <= preorder[i], inorder[i] <= 3000

preorder 和 inorder 均无重复元素

inorder 均出现在 preorder

preorder 保证为二叉树的前序遍历序列

inorder 保证为二叉树的中序遍历序列

Related Topics

树

数组

哈希表

分治

二叉树

解法一：

递归

每次构建 root节点，同时递归构建左右子树的根节点

核心代码在于先序数组构造时的范围

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder, 0, preorder.length,
                inorder, 0, inorder.length);
    }

    private TreeNode build(int[] preorder, int preLeft, int preRight,
                           int[] inorder, int inLeft, int inRight) {
		// base condition
        if (preLeft == preRight) {
            return null;
        }

        // root节点的元素的值
        int rootVal = preorder[preLeft];
        // 找出该值在中序数组中的位置
        int indexIn = 0;
        for (int i = inLeft; i < inRight; i++) {
            if (inorder[i] == rootVal) {
                indexIn = i;
                break;
            }
        }
		// 计算分治时数组的范围
        int leftSize = indexIn - inLeft;
		// 递归构造左右子树
        TreeNode root = new TreeNode(rootVal);
        root.left = build(preorder, preLeft + 1, preLeft + leftSize + 1,
                            inorder, inLeft, indexIn);
        root.right = build(preorder, preLeft + leftSize + 1, preRight,
                            inorder, indexIn + 1, inRight);

        return root;
    }
}

优化：在寻找中序数组中根的位置时，每次都要遍历一遍，相对低效；

可以在一开始就创建一个哈希表 HashMap<Integer, Integer>，键为 inorder[i]，值为 i；

到时候就直接 map.get(rootVa)即可获取下标

第二次手写

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder, 0, preorder.length - 1, 
                        inorder, 0, inorder.length - 1);
    }

    private TreeNode build(int[] preorder, int preLeft, int preRight, 
                            int[] inorder, int inLeft, int inRight) {
        if (preLeft > preRight) {
            return null;
        }

        TreeNode root = new TreeNode(preorder[preLeft]);
        int idx = inLeft;
        for(int i = inLeft; i <= inRight; i++) {
            if (inorder[i] == preorder[preLeft]) {
                idx = i;
                break;
            }
        }
        int leftSize = idx - inLeft;

        TreeNode leftNode = build(preorder, preLeft + 1, preLeft + leftSize, 
                                    inorder, inLeft, inLeft + leftSize - 1);
        TreeNode rightNode = build(preorder, preLeft + leftSize + 1, preRight, 
                                    inorder, inLeft + leftSize + 1, inRight);
        root.left = leftNode;
        root.right = rightNode;

        return root;
    }
}

[106] 从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：
 3
/ \\
9  20
 /  \\
15   7
Related Topics

树

数组

哈希表

分治

二叉树

解法一：

递归

基本同上一题；

核心在于找出构建左右子树时的数组下标相关的值

注意：别直接用 index计算，index代表的是 rootVal的下标，要用的是它和数组左边界间的距离

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return build(inorder, 0, inorder.length,
                postorder, 0, postorder.length);
    }

    private TreeNode build(int[] inorder, int iLeft, int iRight,
                           int[] postorder, int pLeft, int pRight) {

        // base condition
        if (pLeft == pRight) {
            return null;
        }

        int rootVal = postorder[pRight - 1];
        TreeNode root = new TreeNode(rootVal);

        // find and record rootVal in inorder
        int index = iLeft;
        for (int i = iLeft; i < iRight; i++) {
            if (inorder[i] == rootVal) {
                index = i;
                break;
            }
        }

        int distance = index - iLeft;

        root.left = build(inorder, iLeft, iLeft + distance,
                postorder, pLeft, pLeft + distance);

        root.right = build(inorder, iLeft + distance + 1, iRight,
                postorder, pLeft + distance, pRight - 1);

        return root;
    }
}

使用 map存储节点值的做法：

class Solution {
    Map<Integer, Integer> map = new HashMap<>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        // 先存值和下标
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        return build(inorder, 0, inorder.length,
                postorder, 0, postorder.length);
    }

    private TreeNode build(int[] inorder, int iLeft, int iRight,
                           int[] postorder, int pLeft, int pRight) {

        // base condition
        if (pLeft == pRight) {
            return null;
        }

        int rootVal = postorder[pRight - 1];
        TreeNode root = new TreeNode(rootVal);
		// 直接根据值找下标
        int index = map.get(rootVal);

        int distance = index - iLeft;

        root.left = build(inorder, iLeft, iLeft + distance,
                postorder, pLeft, pLeft + distance);

        root.right = build(inorder, iLeft + distance + 1, iRight,
                postorder, pLeft + distance, pRight - 1);

        return root;
    }
}

第二次手写

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return build(inorder, 0, inorder.length - 1, 
                        postorder, 0, postorder.length - 1);
    }

    private TreeNode build(int[] inorder, int inLeft, int inRight, 
                            int[] postorder, int postLeft, int postRight) {
        if (inLeft > inRight || postLeft > postRight) {
            return null;
        }

        int rootVal = postorder[postRight];
        TreeNode root = new TreeNode(rootVal);
        int idx = inLeft;
        for(int i = inLeft; i <= inRight; i++) {
            if (inorder[i] == rootVal) {
                idx = i;
                break;
            }
        }

        int leftSize = idx - inLeft;
        root.left = build(inorder, inLeft, inLeft + leftSize - 1, 
                            postorder, postLeft, postLeft + leftSize - 1);
        root.right = build(inorder, inLeft + leftSize + 1, inRight, 
                            postorder, postLeft + leftSize, postRight - 1);

        return root;
    }
}

[107] 二叉树的层序遍历 Ⅱ

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]
示例 2：
输入：root = [1]
输出：[[1]]
示例 3：
输入：root = []
输出：[]
提示：

树中节点数目在范围 [0, 2000] 内

-1000 <= Node.val <= 1000

Related Topics

树

广度优先搜索

二叉树

解法一：

队列

使用队列进行层序遍历，用 ArrayList承接每一层的数据，返回前 Collections.reverse(list)即可

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if (root == null) {
            return res;
        }
        queue.offer(root);
        while (queue.size() != 0) {
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                TreeNode out = queue.poll();
                list.add(out.val);
                if (out.left != null) {
                    queue.offer(out.left);
                }
                if (out.right != null) {
                    queue.offer(out.right);
                }
            }
            res.add(list);
        }

        // 反转一下
        Collections.reverse(res);
        return res;
    }
}

优化：避免反转，在插入的时候就倒着插，因此可以使用 LinkedList 的 addFirst()

[109] 有序链表转换二叉树

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

   0
  / \\
-3   9
/   /
-10  5

Related Topics

树

二叉搜索树

链表

分治

二叉树

解法一：

每次都找链表中点作为 root，然后将左右子链表拆开来递归

class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        return traverse(head, null);
    }

    private TreeNode traverse(ListNode head, ListNode tail) {
        // 这里是 tail，别写成 null了
        if (head == tail) {
            return null;
        }

        ListNode p = head, q = head;
        while(q != tail && q.next != tail) {
            p = p.next;
            q = q.next.next;
        }

        TreeNode root = new TreeNode(p.val);
        root.left = traverse(head, p);
        root.right = traverse(p.next, tail);

        return root;
    }
}

[116] 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

提示：

树中节点的数量少于 4096
-1000 <= node.val <= 1000

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

解法一：

先序遍历，创建辅助函数进行递归，连接当前节点的左右子节点，连接左右节点的右左子节点

至于右节点的 next，因为初始化时就已经设置为 null了，所以不用管

class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }

        connectTwoNode(root.left, root.right);
        return root;
    }

    private void connectTwoNode(Node node1, Node node2) {
        if (node1 == null || node2 == null) {
            return;
        }

        node1.next = node2;
        connectTwoNode(node1.left, node1.right);
        connectTwoNode(node1.right, node2.left);
        connectTwoNode(node2.left, node2.right);
    }
}

优化：不需要额外使用自定义的递归函数，而是通过 next指针的特性，在当前层构建下一层

class Solution {
    public Node connect(Node root) {
        if(root==null){
            return root;
        }
        
        if(root.left!=null){
            root.left.next=root.right;
            root.right.next=root.next!=null?root.next.left:null;
            connect(root.left);
            connect(root.right);
        }
        return root;
    }
}

解法二：

层序遍历的同时建立 next指针

class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }

        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        // 声明上一个节点，实际建立指针是在 上一个节点和当前节点进行
        Node prev = null;

        while (!queue.isEmpty()) {
            prev = null;
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Node out = queue.poll();
                if (out.left != null) {
                    queue.offer(out.left);
                }
                if (out.right != null) {
                    queue.offer(out.right);
                }

                if (prev != null) {
                    prev.next = out;
                }
                prev = out;
            }
        }

        return root;
    }
}

优化，不需要额外设置指针来表示上一个节点，而是使用 queue.peek()获取下一个结点

class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }

        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Node out = queue.poll();
                
                // 实际建立指针是在 当前节点和下一个结点进行
                if (i != size - 1) {
                    out.next = queue.peek();                    
                }
                
                if (out.left != null) {
                    queue.offer(out.left);
                }
                if (out.right != null) {
                    queue.offer(out.right);
                }
            }
        }
        return root;
    }
}

[117] 填充每个节点的下一个右侧节点指针Ⅱ

给定一个二叉树

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

提示：

树中的节点数小于 6000
-100 <= node.val <= 100

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

解法一：

广度优先遍历

使用队列作为中间存储

class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }
		
        // 声明队列暂存节点
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            // 每一层的第一个结点的前一个节点都是 null
            Node pre = null;
            // 注意这里一定要单独声明出来，不要直接在 for循环里用 queue.size()
            int size = queue.size();

            for (int i = 0; i < size; i++) {
                Node node = queue.poll();
                if (pre != null) {
                    // 指定前一个节点的 next指向当前节点，而初始化时所有节点的 next都是 null，所以当前节点的 next不需要设置
                    pre.next = node;
                }
                // 更新前节点
                pre = node;
                
                // 左右节点入队
                if (node.left != null) {
                    queue.add(node.left);
                }

                if (node.right != null) {
                    queue.add(node.right);
                }
            }

        }

        return root;
    }
}

解法二：

不使用队列，将同一层节点看作是一个链表，next为向后的指针

通过 next指针，遍历上一层为下一层建立联系

class Solution {
    public Node connect(Node root) {

        if (root == null) {
            return root;
        }

        Node cur = root;

        // 遍历多层，在当前层时为下一层建立联系
        while (cur != null) {
            Node pre = new Node(-1), dummy = pre;

            // 遍历某一层
            while (cur != null) {
                // 为前一节点和当前节点建立联系
                // 如果左子节点非空，建立和左子节点的联系
                if (cur.left != null) {
                    pre.next = cur.left;
                    pre = pre.next;
                }
                // 右子节点同理
                if (cur.right != null) {
                    pre.next = cur.right;
                    pre = pre.next;
                }
                // 遍历下一个当前层的结点
                cur = cur.next;
            }
            // dummy自声明后都没有动，只是在第一次 prev.next = xxx时，修改了其 next节点，指向下一层的首元结点
            cur = dummy.next;
        }
        
        return root;
    }
}

[122] 买卖股票的最佳时机Ⅱ

给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
  随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
  注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104

Related Topics

贪心

数组

动态规划

解法一：

贪心

思路是这样的：如果今天的股价比昨天的高，我们就进行一次交易。每天都进行如此判断，可得最大收益。

原因是：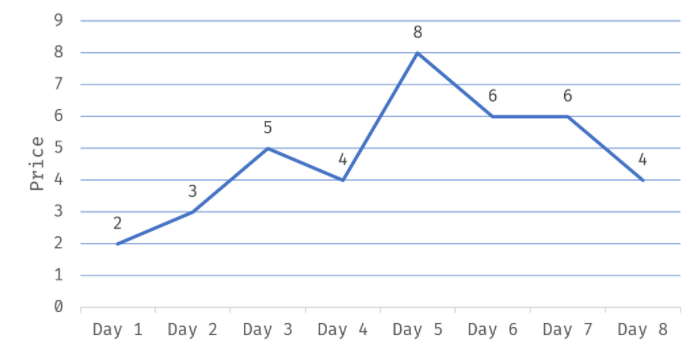

比如说这里：对于 day1购入的股票，day2卖掉还是 day3卖掉的效果是一样的，那么这个时候如果 day2卖掉，并且 day2再买入，到 day3再卖掉，同样能够获得该段时期内的最大收益。

而对于 day3 - day4，因为股价跌了，所以不买入。

而 day4 - day5时因为股价会涨，所以选择在 day4买入，day5卖出。

所以可以将炒股看作一段段的买卖，但是这种方式其实是违背了炒股本身的。

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length <= 1) {
            return 0;
        }

        int sum = 0;
        for (int i = 1; i < prices.length; i++) {
            // 如果能赚钱，我就倒卖一次
            if (prices[i] > prices[i - 1]) {
                sum += (prices[i] - prices[i - 1]);
            }
        }

        return sum;
    }
}

解法二：

创建一个二维数组 int[][] dp = new int[prices.length][2]

dp[][0]表示当前手头的现金，dp[][1]表示当前手头的股票

我们可以得出以下状态方程概念：

dp[i][0]表示第 i天的现金，而此时的现金可能等同于第 i-1 天的现金（没有投资），也可能等同与前一天的股票卖出价+今天的收益

dp[i][1]表示第 i天的股票，同理可能等于第 i-1天的股票，也可能等同于前一天的现金 - 今天的投资

对于初始状态：

dp[0][0]被认作是第 0天交易结束的现金 dp[0][0] = 0
dp[0][1]被认作是第 0天交易结束的股票，dp[0][1] = -prices[0]（我也不晓得为啥）

正确的观念应该是：dp[][0]表示当天不买股票，手头赚的钱；dp[][1]表示当天买了股票后，手头赚的钱，一开始就买股票的话，钱肯定是减少的

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length <= 1) {
            return 0;
        }

        int[][] dp = new int[prices.length][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }

        return dp[prices.length - 1][0];
    }
}

当然，同样的，因为其实就用了两个值，所以不需要整个的数组，只要定义两个变量也可以了

class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length <= 1) {
            return 0;
        }

//        int[][] dp = new int[prices.length][2];
//        dp[0][0] = 0;
//        dp[0][1] = -prices[0];
        int cash = 0;
        int stock = -prices[0];

        int preCashe = cash; // 记录上一个 cashe
        int preStock = stock; // 记录上一个 stock
        for (int i = 1; i < prices.length; i++) {
//            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            cash = Math.max(preCashe, preStock + prices[i]);
//            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
            stock = Math.max(preStock, preCashe - prices[i]);

            preCashe = cash;
            preStock = stock;
        }

        return cash;
//        return dp[prices.length - 1][0];
    }
}

[128] 最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：
输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2：
输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9
提示：

0 <= nums.length <= 105

-109 <= nums[i] <= 109

Related Topics

并查集

数组

哈希表

解法一：

HashSet存值，每次从 nums中取出一个数，若该数在 set中，就向上向下逐位扩散，每次扩散都判断是否在 set中，若存在则删除之

class Solution {
    public int longestConsecutive(int[] nums) {
        HashSet<Integer> set = new HashSet<Integer>();
        for(int x : nums) {
            set.add(x);
        }

        int res = 0;
        for(int x : nums) {
            if (set.remove(x)) {
                int cur = x;
                int curMax = 1;
                // 向下扩散
                while(set.remove(--cur)) {
                    curMax++;
                }

                // 向上扩散
                cur = x;
                while(set.remove(++cur)) {
                    curMax++;
                }
                // 更新最大值
                res = Math.max(res, curMax);
            }
        }

        return res;  
    }
}

[130] 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

Related Topics

深度优先搜索

广度优先搜索

并查集

数组

矩阵

解法一：

DFS

先把四边上的 O替换为 #，然后针对四边上的 O进行递归，将与其相邻的 O也都替换为 #

随后将剩余的 O替换为 X；再将 # 替换回 O

class Solution {

    public void solve(char[][] board) {
        // 一度让我忘记了 长和宽
        int kuan = board.length;
        int chang = board[0].length;

        for (int i = 0; i < kuan; i++) {
            traverse(board, i, 0);
            traverse(board, i, chang - 1);
        }

        for (int i = 0; i < chang; i++) {
            traverse(board, 0, i);
            traverse(board, kuan - 1, i);
        }

        for (int j = 0; j < kuan; j++) {
            for (int k = 0; k < chang; k++) {
                if (board[j][k] == 'O') {
                    board[j][k] = 'X';
                } else if (board[j][k] == '#') {
                    board[j][k] = 'O';
                }
            }
        }

    }

    private void traverse(char[][] board, int x, int y) {
        // base condition，注意 board[x][y] 的判断是 != O，而不是 == X
        if (x < 0 || y >= board[0].length || x >= board.length || y < 0 || board[x][y] != 'O') {
            return;
        }

        if (board[x][y] == 'O') {
            board[x][y] = '#';
        }
        
        traverse(board, x - 1, y);
        traverse(board, x, y - 1);
        traverse(board, x + 1, y);
        traverse(board, x, y + 1);

    }
}

[137] 只出现一次的数字Ⅱ

给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现 三次。请你找出并返回那个只出现了一次的元素。

示例 1：
输入：nums = [2,2,3,2]
输出：3
示例 2：
输入：nums = [0,1,0,1,0,1,99]
输出：99
提示：

1 <= nums.length <= 3 * 104

-231 <= nums[i] <= 231 - 1

nums 中，除某个元素仅出现一次外，其余每个元素都恰出现三次

进阶：你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

Related Topics

位运算

数组

解法一：

排序

class Solution {
    public int singleNumber(int[] nums) {
        Arrays.sort(nums);
        int i = 0;
        while (i < nums.length - 2) {
            if (nums[i] == nums[i + 1] && nums[i] == nums[i + 2]) {
                i += 3;
                continue;
            }

            return nums[i];
        }
        return nums[nums.length - 1];
    }
}

❤ 解法二：

位运算，DFA

如果元素只出现两次，那么可用相同数异或为 0的性质。

但如果，元素出现三次，就需要至少两位进行记录

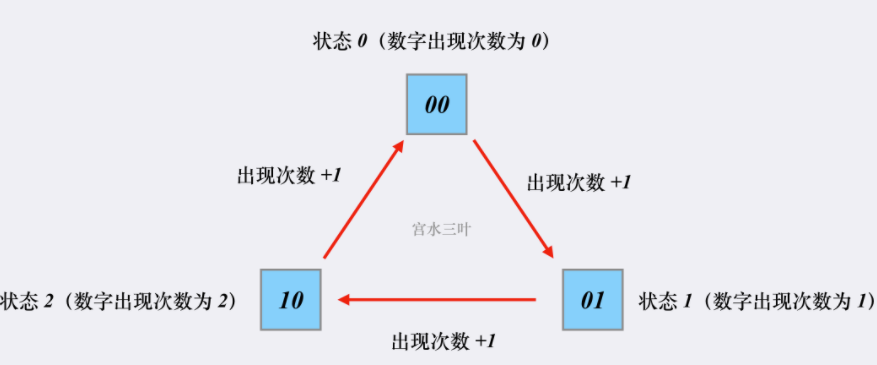
class Solution {
    public int singleNumber(int[] nums) {
        int one = 0, two = 0;
        for (int num : nums) {
            one = one ^ num & ~two;
            two = two ^ num & ~one;
        }
        return one;
    }
}

[138] 复制带随机指针的链表

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的深拷贝。深拷贝应该正好由 n 个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。

新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。
复制链表中的指针都不应指向原链表中的节点。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。
返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

输入：head = []
输出：[]

解法一

先不讨论 random指针域的问题，单纯完成链表的 val 和 next的深拷贝

然后再遍历老链表中的每一个结点，找到它的 random指针指向链表中的第几个结点；然后在新链表中通过给定结点的索引位置，进行 random域的赋值

class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) {
            return null;
        }
        // 先把链表的基础结构搭建好
        Node first = new Node(head.val);
        Node p = first, q = head;
        while (q.next != null) {
            Node node = new Node(q.next.val);
            p.next = node;
            p = p.next;
            q = q.next;
        }

        // 重新遍历链表，找 random，赋值 random
        p = first;
        q = head;
        while (p != null && q != null) {
            Integer index = getIndex(q, head);
            if (index == null) {
                p.random = null;
            } else {
                p.random = setIndex(index, first);
            }
            p = p.next;
            q = q.next;
        }
        // 返回新链表的首元结点
        return first;
    }

    public static Integer getIndex(Node node, Node head) {
        Node want = node.random;
        if (want == null) {
            return null;
        }
        int count = 0;
        while (head != null && !head.equals(want)) {
            head = head.next;
            count++;
        }
        return count;
    }

    public static Node setIndex(Integer count, Node head) {
        while (head != null && count > 0) {
            count--;
            head = head.next;
        }

        return head;
    }
}

解法二

回溯+哈希表

利用回溯的方式，让每个结点的拷贝相互独立。

对于当前结点，我们首先进行拷贝，然后我们进行 当前结点的后继结点 和 当前结点的 random结点 的拷贝，拷贝完成后将创建的新结点的指针返回，即可完成当前结点的两个指针的赋值。

具体的，为了记录每个结点的创建情况，我们用哈希表来实现。

具体步骤如下：

检查当前节点的后继节点创建情况
- 如果没有创建，递归创建，成功之后就赋值
- 如果已经创建了，就直接赋值
检查当前结点的 random结点的创建情况，大致同上
如果一个结点被多个节点引用，为了避免重复拷贝，我们需要使用哈希表提前检查

class Solution {
    // 定义全局的哈希表
    Map<Node, Node> cachedNode = new HashMap<>();

    public Node copyRandomList(Node head) {
        if(head == null) {
            return null;
        }

        if(!cachedNode.containsKey(head)) {
            Node headNew = new Node(head.val);
            cachedNode.put(head, headNew);
            headNew.next = copyRandomList(head.next);
            headNew.random = copyRandomList(head.random);
        }

        return cachedNode.get(head);
    }
}

解法三

迭代 + 结点拆分

将每一个结点拆分成两个相连的节点，例如：A -> B -> C 将拆分为 A -> A’-> B -> B’-> C -> C’；对于任意一个节点，其拷贝节点即为其后继节点。

所以拷贝节点的 random指针应该指向的是原节点的 random指向的节点的拷贝节点

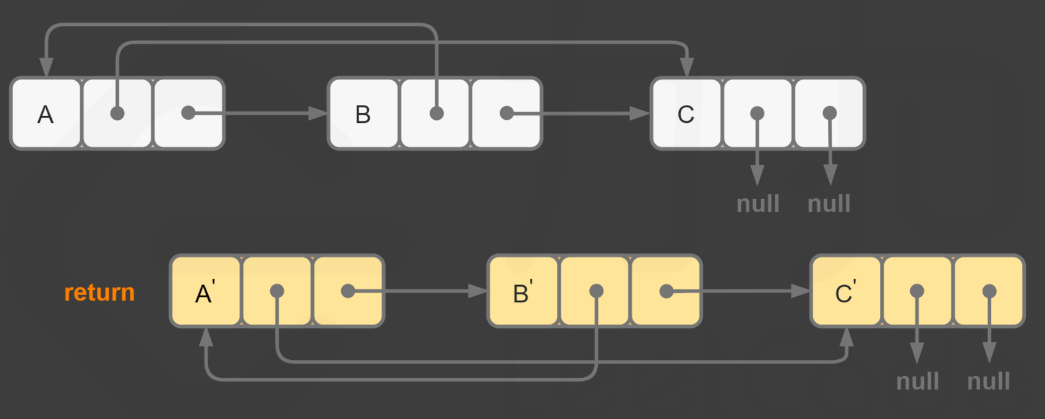
public class Solution {
    public Node CopyRandomList(Node head) {
        if (head == null) {
            return null;
        }
        // 先将链表扩容成原来的一倍，新节点中还未存 random
        for (Node node = head; node != null; node = node.next.next) {
            Node newNode = new Node(node.val);
            newNode.next = node.next;
            node.next = newNode;
        }

        // 遍历链表，实现 random的赋值，注意，random的值为拷贝节点
        for(Node node = head; node != null; node = node.next.next) {
            Node newNode = node.next;
            newNode.random = (node.random != null) ? node.random.next : null;
        }

        // 再把每一个拷贝节点串起来
        Node newHead = head.next;
        for (Node node = head; node != null; node = node.next) {
            Node newNode = node.next;
            node.next  = node.next.next;
            newNode.next = (newNode.next != null) ? newNode.next.next : null;
        }

        return newHead;
    }
}

[139] 单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2：
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
  注意，你可以重复使用字典中的单词。
示例 3：
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
提示：

1 <= s.length <= 300

1 <= wordDict.length <= 1000

1 <= wordDict[i].length <= 20

s 和 wordDict[i] 仅有小写英文字母组成

wordDict 中的所有字符串 互不相同

Related Topics

字典树

记忆化搜索

哈希表

字符串

动态规划

解法一：

dp[n]代表到 n为止是否都能被集合中的值替换；

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        HashSet<String> set = new HashSet<>(wordDict);
        // dp[n] 代表字符串中到 n 为止是否都能由 wordDict中的字符串组成
        boolean[] dp = new boolean[s.length() + 1];
        dp[0] = true;

        for(int i = 1; i <= s.length(); i++) {
            for(int j = 0; j < i; j++) {
                // 其实判断在到 j 为止都可以组成的情况下， (j, i) 在不在集合中
                if (dp[j] && set.contains(s.substring(j, i))) {
                    dp[i] = true;
                }
            }
        }

        return dp[s.length()];
    }
}

[142] 环形链表Ⅱ

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

进阶：

你是否可以使用 O(1) 空间解决此题？

示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：
输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。
提示：

链表中节点的数目范围在范围 [0, 104] 内

-105 <= Node.val <= 105

pos 的值为 -1 或者链表中的一个有效索引

Related Topics

哈希表

链表

双指针

解法一：

使用 Hashset判断是否重复，如果重复则返回重复的节点；否则返回 null

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null) {
            return null;
        }

        HashSet<ListNode> set = new HashSet<ListNode>();
        while (head != null) {
            if (!set.add(head)) {
                return head;
            }
            head = head.next;
        }
        return null;
    }
}

解法二：

依旧使用快慢指针，但是要考虑数学公式了。。。

首先还是原来的思想，快慢指针重合后表示成环。

设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc。

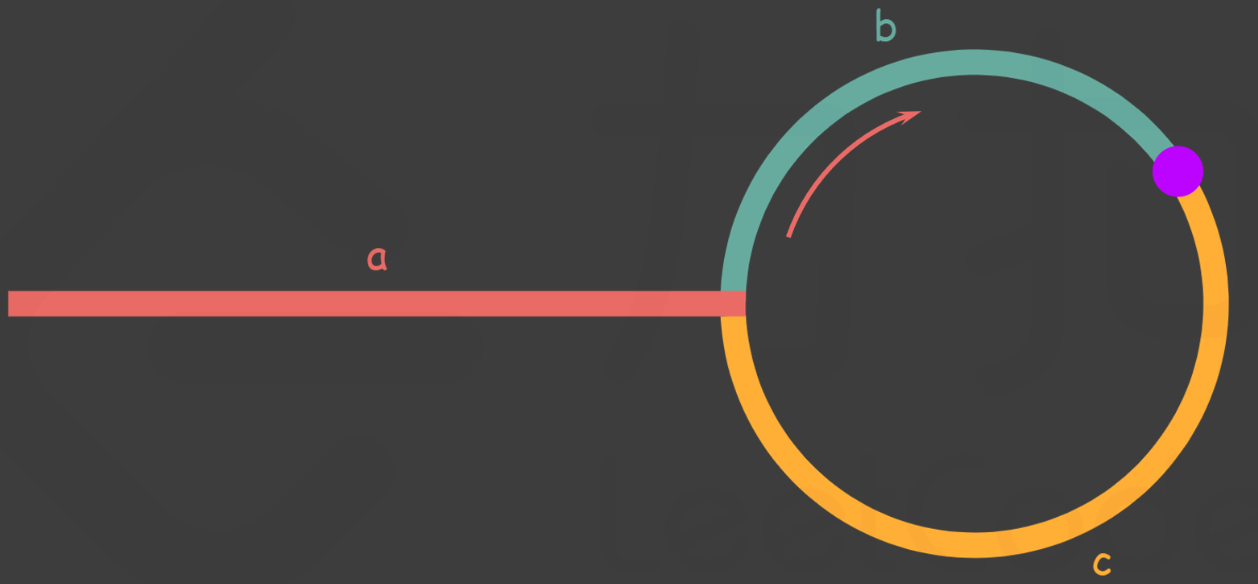
任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，我们有

a + (n + 1) b+n * c= 2 (a + b) ⟹ a = c + (n − 1)(b + c)

因此，当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        // 判空
        if (head == null || head.next == null) {
            return null;
        }

        // 声明快慢指针
        ListNode fast = head, slow = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;

            if(fast == slow) {
                break;
            }
        }

        if (fast != slow) {
            return null;
        }

        // 套上述的数学公式
        fast = head;
        while (fast != slow) {
            fast = fast.next;
            slow = slow.next;
        }

        return slow;
    }
}

[143] 重排链表

给定一个单链表 L 的头节点 head ，单链表 L 表示为：
L0 → L1 → … → Ln-1 → Ln
请将其重新排列后变为：
L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → …

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

输入: head = [1,2,3,4]
输出: [1,4,2,3]

输入: head = [1,2,3,4,5]
输出: [1,5,2,4,3]

解法一：

采用快慢指针定位哪些节点需要进行重排，采用栈进行链表倒排

class Solution {
    public void reorderList(ListNode head) {

        if (head == null || head.next == null) {
            return;
        }

        // 声明快慢指针
        ListNode fast = head;
        ListNode slow = head;

        // 慢指针每次走一格，快指针走两格，当快指针到达尾部后，慢指针恰好到原来指针的一半
        // 此时慢指针之后的所有节点都需要在重排时作插入用
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }

        // 在 slow之后将原来的链表打断，避免产生环
        ListNode newHead = slow.next;
        slow.next = null;

        // 通过 LinkedList将 slow之后的节点排成倒序
        LinkedList<ListNode> list = new LinkedList<>();
        while (newHead != null) {
            list.addLast(newHead);
            newHead = newHead.next;
        }

        // 从原链表头部开始
        newHead = head;
        ListNode newHeadNxt = head.next;
        // 从 Linklist中倒着取出节点，插入，然后那些指针都向后移动
        // 注意：list.removeLast()在 list为空时会报异常
        while (!list.isEmpty()) {
            ListNode ins = list.removeLast();
            newHead.next = ins;
            ins.next = newHeadNxt;
            newHead = newHeadNxt;
            newHeadNxt = newHead.next;
        }
    }
}

解法二：

依旧使用双指针，但是使用递归进行链表的倒排。

[146] ❤ LRU 缓存机制

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。

实现 LRUCache 类：

LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字-值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

进阶：你是否可以在 O(1) 时间复杂度内完成这两种操作？

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]

输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
LRUCache.put(1, 1); // 缓存是 {1=1}
LRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
LRUCache.get(1); // 返回 1
LRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
LRUCache.get(2); // 返回 -1 (未找到)
LRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
LRUCache.get(1); // 返回 -1 (未找到)
LRUCache.get(3); // 返回 3
LRUCache.get(4); // 返回 4

解法一：

使用 Java中自带的 LinkedHashMap来存储

LinkedHashMap是有两种排序方式：按照插入顺序排序和按照读取顺序排序，内部依靠一个双向链表维护顺序。

在每次的插入、删除、读取之后都会有一个回调函数进行链表的维护

void afterNodeAccess(Node<K, V> p) { }在访问元素之后，将该元素放到双向链表的尾部（只有在开启按照读取顺序排序之后才会生效）
void afterNodeRemoval(Node<K, V> p) { } 在删除元素之后，将元素从双向链表中删除
void afterNodeInsertion(Node<K, V> p) { } 在插入新的元素之后，判断容器是否超载，要移除旧的元素

/**
* LinkedHashMap中的一些源码
*/
public LinkedHashMap() { 
    super(); 
    // 这里的 accessOrder 默认是为false，如果要按读取顺序排序需要将其设为 true
    accessOrder = false; 
}

public LinkedHashMap(int initialCapacity, float loadFactor, boolean accessOrder) { 
    super(initialCapacity, loadFactor); 
    this.accessOrder = accessOrder; 
}

/** 
* 插入新节点才会触发该方法，因为只有插入新节点才需要内存 
* 根据 HashMap 的 putVal 方法, evict 一直是 true 
* removeEldestEntry 方法表示移除规则, 在 LinkedHashMap 里一直返回 false 
* 所以在 LinkedHashMap 里这个方法相当于什么都不做 
*/
void afterNodeInsertion(boolean evict) { // possibly remove eldest 
    LinkedHashMap.Entry<K,V> first; 
    // 根据条件判断是否移除最近最少被访问的节点 
    if (evict && (first = head) != null && removeEldestEntry(first)) { 
        K key = first.key; 
        removeNode(hash(key), key, null, false, true); 
    } 
}

// 移除最近最少被访问条件之一，通过覆盖此方法可实现不同策略的缓存 
// LinkedHashMap是默认返回false的，我们可以继承LinkedHashMap然后复写该方法即可 
protected boolean removeEldestEntry(Map.Entry<K,V> eldest) { 
    return false; 
}

通过上述代码，我们就已经知道了只要复写 removeEldestEntry() 即可，而条件就是 map 的大小不超过给定的容量，超过了就得使用 LRU 了！

class LRUCache extends LinkedHashMap<Integer, Integer> {
    private int capacity;

    public LRUCache(int capacity) {
        super(capacity, 0.75F, true); // true表示按照读取顺序排序
        this.capacity = capacity;
    }

    public int get(int key) {
        // getOrDefault()方法可以实现这样的效果：如果有就value，否则返回一个指定的值
        return super.getOrDefault(key, -1);
    }

    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity;
    }
}

帅张那里的解法，更直观

class LRUCache {
    int cap;
    LinkedHashMap‹Integer, Integer› cache = new LinkedHashMap‹›();
    public LRUCache(int capacity) { 
        this.cap = capacity;
    }
    
    public int get(int key) {
        if (!cache.containsKey(key)) {
            return -1;
        }
        // 将 key 变为最近使用
        makeRecently(key);
        return cache.get(key);
    }
    
    public void put(int key, int val) {
        if (cache.containsKey(key)) {
            // 修改 key 的值
            cache.put(key, val);
            // 将 key 变为最近使用
            makeRecently(key);
            return;
        }
        
        if (cache.size() ›= this.cap) {
            // 链表头部就是最久未使用的 key
            int oldestKey = cache.keySet().iterator().next();
            cache.remove(oldestKey);
        }
        // 将新的 key 添加链表尾部
        cache.put(key, val);
    }
    
    private void makeRecently(int key) {
        int val = cache.get(key);
        // 删除 key，重新插入到队尾
        cache.remove(key);
        cache.put(key, val);
    }
}

解法二：

使用 HashMap和自定义的双向链表实现

双向链表按照被使用的顺序存储节点
哈希表通过键映射到其在双向链表中的节点的位置

我们在 get()的时候，会先通过 HashMap以 O(1)的开销定位节点，并且因为是双向链表，所以可以直接将其移动到原链表的头部。

我们在 put()的时候，先检查 HashMap中键是否存在：如果存在，类似 get()方法，并且将该节点的值进行更新；如果不存在，就创建新的节点，添加到链表头部和哈希表中，如果容量超额了，就移除掉一个链表尾部的节点。

public class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        // 前驱指针
        DLinkedNode prev;
        // 后继指针
        DLinkedNode next;

        public DLinkedNode() {
        }

        public DLinkedNode(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }

    // value为 Node，便于删除操作
    private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
    // 当前的链表节点个数
    private int size;
    // 最大可存储的个数
    private int capacity;
    // dummy head, dummy tail
    private DLinkedNode head, tail;


    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;

        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        } 
        // 如果 key 存在，先通过哈希表定位，再移到头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) { 
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode newNode = new DLinkedNode(key, value); 
            // 添加进哈希表
            cache.put(key, newNode); 
            // 添加至双向链表的头部
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode tail = removeTail(); 
                // 删除哈希表中对应的项
                cache.remove(tail.key);
                --size;
            }
        } else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;
            moveToHead(node);
        }
    }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}

帅张处的解法，命名上更加直观

public class LRUCache {
    private HashMap<Integer, Node> map;
    private DoubleLinkedList cache;
    private int capacity;

    public LRUCache(int capacity) {
        this.capacity = capacity;
        map = new HashMap<>();
        cache = new DoubleLinkedList();
    }

    public int get(int key) {
        if (!map.containsKey(key)) {
            return -1;
        }
        makeRecent(key);
        return map.get(key).val;
    }

    public void put(int key, int value) {
        // 注意顺序，先判断键是否存在，然后再判断 size
        if (map.containsKey(key)) {
            deleteKey(key);
            addRecent(key, value);
            return;
        }

        if (capacity == cache.size) {
            removeLeastRecentlyUsed();
        }

        addRecent(key, value);
    }

    /**
     * 将某个节点设为最近使用
     *
     * @param key
     */
    private void makeRecent(int key) {
        Node node = map.get(key);
        cache.remove(node);
        cache.addLast(node);
    }

    private void addRecent(int key, int val) {
        Node node = new Node(key, val);
        map.put(key, node);
        cache.addLast(node);
    }

    private void deleteKey(int key) {
        Node node = map.get(key);
        map.remove(key);
        cache.remove(node);
    }

    private void removeLeastRecentlyUsed() {
        Node node = cache.removeFirst();
        map.remove(node.key);
    }

    /**
     * 定义节点
     */
    class Node {
        int key, val;
        Node prev, next;

        public Node() {
        }

        public Node(int key, int val) {
            this.key = key;
            this.val = val;
        }
    }

    class DoubleLinkedList {
        // 头尾节点
        private Node tail, head;
        // 链表元素数量
        private int size;

        /**
         * 初始化链表
         */
        public DoubleLinkedList() {
            head = new Node(0, 0);
            tail = new Node(0, 0);

            head.next = tail;
            tail.prev = head;
            size = 0;
        }

        /**
         * 在链表尾部添加节点
         *
         * @param x
         */
        public void addLast(Node x) {
            x.prev = tail.prev;
            x.next = tail;
            tail.prev.next = x;
            tail.prev = x;
            size++;
        }

        /**
         * 移除指定的某一个节点
         *
         * @param x
         */
        public void remove(Node x) {
            x.prev.next = x.next;
            x.next.prev = x.prev;
            // 将对 size的操作统一封装在 remove()和 addLast()方法中
            size--;
        }

        /**
         * 移除并返回链表中的第一个节点
         *
         * @return
         */
        public Node removeFirst() {
            if (head.next == tail) {
                return null;
            }

            Node first = head.next;
            remove(first);
            return first;
        }

        public int size() {
            return size;
        }
    }
}

[147] 对链表进行插入排序

对链表进行插入排序。

从第一个元素开始，该链表可以被认为已经部分排序。每次迭代时，从输入数据中移除一个元素，并原地将其插入到已排好序的链表中。

插入排序算法：
插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
重复直到所有输入数据插入完为止。

示例 1：
输入: 4->2->1->3
输出: 1->2->3->4

示例 2：
输入: -1->5->3->4->0
输出: -1->0->3->4->5

解法一：

就依据题目描述的一样，从第一个元素开始，对链表进行排序，每次迭代时对一个元素进行处理。

class Solution {
    public ListNode insertionSortList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        // 设立头节点
        ListNode dummy = new ListNode(-1, head);

        ListNode lastNode = head;
        ListNode curr = head.next;

        // 一个循环保证每个节点都会进行一次判断
        while (curr != null) {

            // 如果不需要插排的话
            if (lastNode.val < curr.val) {
                lastNode = lastNode.next;
            } else {
                ListNode prev = dummy;
                // 定位到待插入的位置
                while (prev.next.val < curr.val) {
                    prev = prev.next;
                }

                // 在原链表中去除 原curr节点
                lastNode.next = curr.next;
                // 在链表的前面插入 curr
                curr.next = prev.next;
                prev.next = curr;
            }
            // 表示当前节点已经完成插排工作，进行下一个结点的任务
            curr = lastNode.next;
        }
        return dummy.next;
    }
}

[148] ❤ 排序链表

给你链表的头结点 head ，请将其按升序排列并返回排序后的链表。

进阶：
你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

示例 1：
输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：
输入：head = []
输出：[]

解法一：

就是上一题的题解，使用插排

class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        ListNode dummy = new ListNode(-1, head);
        ListNode lastSort = head;
        ListNode curr = head.next;

        while (curr != null) {
            if (lastSort.val < curr.val) {
                lastSort = lastSort.next;
            } else {
                ListNode prev = dummy;
                while (prev.next.val < curr.val) {
                    prev = prev.next;
                }
                lastSort.next = curr.next;
                curr.next = prev.next;
                prev.next = curr;
            }
            curr = lastSort.next;
        }
        return dummy.next;
    }
}

解法二：

自顶向下的归并排序：

快慢指针找到链表的中点，将其拆分成两个子链表
对两个子链表分别排序
将两个子链表合并

上述步骤递归实现，递归终止的条件是节点个数小于或等于1，以至于无法继续拆分

class Solution {
    public ListNode sortList(ListNode head) {
        return mergeSort(head, null);
    }

    /**
    * 拆分链表并且递归调用
    */
    private ListNode mergeSort(ListNode head, ListNode tail) {
        // 递归结束的条件
        if (head == null) {
            return head;
        }
        if (head.next == tail) {
            head.next = null;
            return head;
        }
        // 快慢指针，找到链表的中点
        ListNode slow = head;
        ListNode fast = head;
        while (fast != tail && fast.next != tail) {
            slow = slow.next;
            fast = fast.next.next;
        }
        // 递归调用
        ListNode mid = slow;
        ListNode list1 = mergeSort(head, mid);
        ListNode list2 = mergeSort(mid, tail);
        // 合并链表，实际上两个单独的节点，就是通过合并操作排序的
        ListNode sorted = mergeList(list1, list2);
        return sorted;
    }

    /**
    * 合并两个链表
    */
    private ListNode mergeList(ListNode head1, ListNode head2) {
        ListNode p = head1, q = head2;
        ListNode r = new ListNode();
        ListNode s = r;

        while (p != null && q != null) {
            if (p.val < q.val) {
                r.next = p;
                p = p.next;
                r = r.next;
            } else {
                r.next = q;
                q = q.next;
                r = r.next;
            }
        }
        r.next = p != null ? p : q;
        return s.next;
    }
}

解法三：

自底向上归并链表

每次将链表拆分成若干个 subLength长度的子链表，按照两个子链表一组合并
将 subLength长度 * 2，重复第 1步直到有序子链表的长度大于或等于整个链表的长度

class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        // 统计链表的长度
        int length = 0;
        ListNode node = head;
        while (node != null) {
            length++;
            node = node.next;
        }

        ListNode dummy = new ListNode();
        dummy.next = head;
        // 每次 subLength翻倍，依据 subLength划分子链表，每两个子链表合并一次
        for (int subLength = 1; subLength < length; subLength <<= 1) {
            ListNode prev = dummy, cur = dummy.next;

            while (cur != null) {
                // 切割得到第一个子链表
                ListNode head1 = cur;
                for (int i = 1; i < subLength && cur.next != null; i++) {
                    cur = cur.next;
                }

                // 切割得到第二个子链表
                ListNode head2 = cur.next;
                cur.next = null;
                cur = head2;
                for (int i = 1; i < subLength && cur != null && cur.next != null; i++) {
                    cur = cur.next;
                }
                // 记得把第二个子链表截断，避免多余的节点参与合并
                ListNode nxt = null;
                if (cur != null) {
                    nxt = cur.next;
                    cur.next = null;
                }

                // 得到合并后的大子链表
                ListNode merged = mergeList(head1, head2);
                prev.next = merged;
                // 定位 prev到最后
                while (prev.next != null) {
                    prev = prev.next;
                }
                // 继续向后切割两个小子链表
                cur = nxt;
            }
        }
        return dummy.next;
    }

    private ListNode mergeList(ListNode head1, ListNode head2) {
        ListNode p = head1, q = head2;
        ListNode r = new ListNode();
        ListNode s = r;

        while (p != null && q != null) {
            if (p.val < q.val) {
                r.next = p;
                p = p.next;
                r = r.next;
            } else {
                r.next = q;
                q = q.next;
                r = r.next;
            }
        }
        r.next = p != null ? p : q;
        return s.next;
    }
}

[152] 乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

子数组 是数组的连续子序列。

示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:

1 <= nums.length <= 2 * 104

-10 <= nums[i] <= 10

nums 的任何前缀或后缀的乘积都保证是一个 32-位 整数

Related Topics

数组

动态规划

解法一：

因为存在负数，所以单纯的一维数组不够，单纯的一维数组只能记录到 i 为止，最大的乘积；

而由于负数的存在，会立刻让原本最小的值变成最大的值，所以需要维护两个数组；

一个记录最小值，另一个记录最大值；

又由于每次计算都只跟上一个值有关，所以可以不需要数组，只用两个数来代替两个数组就行

class Solution {
    public int maxProduct(int[] nums) {

        int max = Integer.MIN_VALUE;
        
        // 分别代表当前的最大值 和 当前的最小值
        int imax = 1, imin = 1;
        for(int x : nums) {
            // 如果碰到负数了，那么最大值和最小值就会互换
            if (x < 0) {
                int tmp = imax;
                imax = imin;
                imin = tmp;
            }

            // 维护当前最大/小值，要么是当前值，要么和前面的值有关
            imax = Math.max(x, imax * x);
            imin = Math.min(x, imin * x);
            // 维护全局最大值
            max = Math.max(max, imax);
        }

        return max;
    }
}

[167] 两数之和Ⅱ - 输入有序数组

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：
输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2：
输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3：
输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
提示：

2 <= numbers.length <= 3 * 104

-1000 <= numbers[i] <= 1000

numbers 按 非递减顺序 排列

-1000 <= target <= 1000

仅存在一个有效答案

Related Topics

数组

双指针

二分查找

解法一：

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int len = numbers.length;
        int left = 0, right = len - 1;
		// 虚假的二分查找
        while (left < right) {
            int sum = numbers[left] + numbers[right];
            if (sum == target) {
                return new int[]{left + 1, right + 1};
            }
            if (sum < target) {
                left++;
            } else {
                right--;
            }
        }

        return numbers;
    }
}

[189] 轮转数组

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示：

1 <= nums.length <= 105

-231 <= nums[i] <= 231 - 1

0 <= k <= 105

进阶：

尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。

你可以使用空间复杂度为 O(1) 的原地算法解决这个问题吗？

Related Topics

数组

数学

双指针

解法一：

另建一个数组 int[] res = new int[nus.length + (nums.length - 1)]

把东西都存过去，然后再存过来

class Solution {


    public void rotate(int[] nums, int k) {
        if (nums.length == 1) {
            return;
        }
        // 这个k有时候会给得比 nums长，所以可以取一个模
        k = k % nums.length;
        if (k == 0) {
            return;
        }
        
        int fast = 0, slow = 0;
        int[] res = new int[nums.length + (nums.length - k)];

        // 先把 nums[]里的所有元素都扔进 res[]里面
        for (int i = 0; i < nums.length; i++) {
            res[i] = nums[i];
        }

        // 快慢指针定位
        for (int i = 0; i < k; i++) {
            fast++;
        }

        while (fast < nums.length) {
            fast++;
            slow++;
        }

        // 把慢指针前面的元素再扔进 res中
        for (int i = nums.length, j = 0; j < slow; i++) {
            res[i] = nums[j];
            j++;
        }


        // 截取 res中 slow之后的内容，扔回 nums中
        for (int i = 0, j = slow; i < nums.length; i++) {
            nums[i] = res[j];
            j++;
        }
    }
}

优化一下， int[] res = new int[nums.length - k]
只存需要往前移动的元素

class Solution {
    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        if (nums.length == 1 || k == 0) {
            return;
        }

        int[] res = new int[nums.length - k];

        int slow = 0, fast = 0;
        for (int i = 0; i < k; i++) {
            fast++;
        }
        while (fast < nums.length) {
            fast++;
            slow++;
        }

        for (int i = 0, j = 0; i < slow; i++) {
            res[j] = nums[i];
            j++;
        }

        int j = 0;
        for (int i = slow; i < nums.length; i++) {
            nums[j] = nums[i];
            j++;

        }

        for (int i = 0; i < res.length; i++) {
            nums[j] = res[i];
            j++;
        }
    }
}

❤ 解法二：

数组反转

对元素的移动等同于对数组进行三次反转

先全部反转，然后分别反转前后两部分

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k %= n;
        reverse(nums, 0, n - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, n - 1);
    }

    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int tmp = nums[end];
            nums[end--] = nums[start];
            nums[start++] = tmp;
        }
    }
}

[200] 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出：1
示例 2：
输入：grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出：3
提示：

m == grid.length

n == grid[i].length

1 <= m, n <= 300

grid[i][j] 的值为 '0' 或 '1'

Related Topics

深度优先搜索

广度优先搜索

并查集

数组

矩阵

解法一：

每计算一座岛屿，就把一座岛屿击沉

class Solution {
    public int numIslands(char[][] grid) {
        int res = 0;
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                // 只要是 1，就肯定是一座岛
                if (grid[i][j] == '1') {
                    res++;
                    // 记录完之后，让海水将它淹没
                    sink(grid, i, j);
                }
            }
        }

        return res;
    }

    private void sink(char[][] grid, int i, int j) {
        if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0') {
            return;
        }
		
        // 把它设置为 1
        grid[i][j] = '0';

        // 横向、纵向淹没
        sink(grid, i - 1, j);
        sink(grid, i + 1, j);
        sink(grid, i, j - 1);
        sink(grid, i, j + 1);
    }
}

[198] 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
  偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
  偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 400

Related Topics

数组

动态规划

解法一：

创建数组 int[] dp = new int[nums.length]，dp[i]表示：当把 nums[i]的钱偷了之后，到此为止，能拿到的最多的钱

迭代方程为：dp[i] = Math.max(dp[i-2]+nums[i], dp[i-3]+nums[i])

举例：

A -> B -> C -> D -> E -> F

如果本次偷 F的钱，那么上一次可能偷 D或者 C的钱

但绝对不可能是 E 和 B，因为 E和 F紧邻，而 B和 F隔得太远了

class Solution {
    public int rob(int[] nums) {

        if (nums.length == 1) {
            return nums[0];
        } else if (nums.length == 2) {
            return Math.max(nums[0], nums[1]);
        } else if (nums.length == 3) {
            return Math.max(nums[0] + nums[2], nums[1]);
        }

        // dp[i]表示到 nums[i]时，选中 num[i] 能收到的最多的钱
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = nums[1];
        dp[2] = dp[0] + nums[2];
        int max = Math.max(dp[2], dp[1]);

        for (int i = 3; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 3] + nums[i]);
            max = Math.max(max, dp[i]);
        }

        return max;
    }
}

第二次手写

class Solution {
    public int rob(int[] nums) {
        if (nums.length == 1) {
            return nums[0];
        }
        
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = nums[1];
        int max = Math.max(dp[0], dp[1]);

        for(int i = 2; i < nums.length; i++) {
            // 如果把数组声明成 nums.length + 1，就可以省略下面的判断
            if (i-2 > 0) {
                dp[i] = Math.max(dp[i-1], Math.max(dp[i-2] + nums[i], dp[i-3] + nums[i]));
            } else 
                dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);
            max = Math.max(dp[i], max);
        }

        return max;
    }
}

[208] 实现 Trie(前缀树)

Trie（发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True
提示：

1 <= word.length, prefix.length <= 2000

word 和 prefix 仅由小写英文字母组成

insert、search 和 startsWith 调用次数总计不超过 3 * 104 次

Related Topics

设计

字典树

哈希表

字符串

解法一：

使用 Trie[] 表示当前层的所有子节点，因为有 26 个字母，所以是数组容量为 26；

因为要 search，所以对于该字符串，最后一个节点后不能再有值，此时就需要额外添加一个标志位 isEnd，否则就需要遍历一轮 children才行了；

注意：对 children的引用都必须写成 node.children，否则引用到的都是根节点的 children

class Trie {

    Trie[] children;
    boolean isEnd;

    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }
    
    public void insert(String word) {
        Trie node = this;
        for(int i = 0; i < word.length(); i++) {
            if (node.children[word.charAt(i) - 'a'] == null) {
                node.children[word.charAt(i) - 'a'] = new Trie();
            }
            node  = node.children[word.charAt(i) - 'a'];
        }
        node.isEnd = true;

    }
    
    public boolean search(String word) {
        Trie lastNode = getLastCharInStr(word);
        return lastNode != null && lastNode.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        return getLastCharInStr(prefix) != null;
    }

    private Trie getLastCharInStr(String word) {
        Trie node = this;
        for(int i = 0; i < word.length(); i++) {
            if (node.children[word.charAt(i) - 'a'] == null) {
                return null;
            }
            node  = node.children[word.charAt(i) - 'a'];
        }
        return node;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

[207] 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。
提示：

1 <= numCourses <= 105

0 <= prerequisites.length <= 5000

prerequisites[i].length == 2

0 <= ai, bi < numCourses

prerequisites[i] 中的所有课程对 互不相同

Related Topics

深度优先搜索

广度优先搜索

图

拓扑排序

解法一：

DFS

class Solution {

    boolean hasCircle = false;
    boolean[] visited;
    boolean[] path;

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        visited = new boolean[numCourses];
        path = new boolean[numCourses];
        // 构建图
        List<Integer>[] graph = build(numCourses, prerequisites);
        // 遍历图
        for (int i = 0; i < numCourses; i++) {
            traverse(i, graph);
        }
        return !hasCircle;
    }

    /**
     * 以邻接表的形式返回
     *
     * @param numCourses
     * @param prerequisites
     * @return
     */
    private List<Integer>[] build(int numCourses, int[][] prerequisites) {
        // 图中共有 numCourses个节点
        List<Integer>[] graph = new List[numCourses];
        for (int i = 0; i < numCourses; i++) {
            graph[i] = new ArrayList<>();
        }

        for (int[] arr : prerequisites) {
            int to = arr[0];
            int from = arr[1];
            graph[from].add(to);
        }

        return graph;
    }

    private void traverse(int v, List<Integer>[] graph) {
        // 判断是否成环
        if (path[v] == true) {
            hasCircle = true;
            return;
        }

        if (visited[v] == true || hasCircle == true) {
            return;
        }

        visited[v] = true;
        path[v] = true;
        for (int s : graph[v]) {
            traverse(s, graph);
        }
        path[v] = false;
    }
}

解法二：

BFS

class Solution {
    // 记录入度
    int[] indeg;

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        indeg = new int[numCourses];
        // 记录图
        List<List<Integer>> graph = build(numCourses, prerequisites);
        // 队列中存储当前可被移除的节点，即入度为 0的节点
        Queue<Integer> queue = new LinkedList<>();
        // 入度为零的入队
        for (int i = 0; i < indeg.length; i++) {
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }

        // 记录访问的次数
        int visited = 0;
        while (!queue.isEmpty()) {
            visited++;
            Integer out = queue.poll();
            // 遍历所有的出度节点
            for (int i : graph.get(out)) {
                indeg[i]--;
                // 如果入度为零，则表示该节点即将被移除，因此入队
                if (indeg[i] == 0) {
                    queue.offer(i);
                }
            }
        }

        return visited == numCourses;
    }

    private List<List<Integer>> build(int numCourses, int[][] prerequisites) {
        List<List<Integer>> graph = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            graph.add(new ArrayList<Integer>());
        }

        for (int[] arr : prerequisites) {
            int to = arr[0];
            int from = arr[1];
            graph.get(from).add(to);
            // 记录入队数量
            indeg[to]++;
        }

        return graph;
    }
}

[209] 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：
输入：target = 4, nums = [1,4,4]
输出：1
示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0
提示：

1 <= target <= 109

1 <= nums.length <= 105

1 <= nums[i] <= 105

进阶：

如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

Related Topics

数组

二分查找

前缀和

滑动窗口

解法一：

滑动窗口

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int res = Integer.MAX_VALUE;
        // sum维护了滑动窗口中的和
        int left = 0, right = 0, sum = 0;

        while (right < nums.length) {
            while (sum >= target) {
                res = Math.min(res, right - left);
                sum -= nums[left++];
            }

            sum += nums[right++];
        }
		// 因为前面是先判断 sum和 left，再处理 right的，那么最后 right到底后，其实 left会缺少一部分处理
        // 因此需要再处理一遍
        // 上面也可以先 sum += num[right]，然后判断是否大于 target，最后再 right++，这样就可以省掉下一步了
        while (sum >= target && left < nums.length) {
            res  = Math.min(res, right - left);
            sum -= nums[left++];
        }

        return res == Integer.MAX_VALUE ? 0 : res;
    }
}

[210] 课程表Ⅱ

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前必须先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
示例 2：
输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3：
输入：numCourses = 1, prerequisites = []
输出：[0]
提示：

1 <= numCourses <= 2000

0 <= prerequisites.length <= numCourses * (numCourses - 1)

prerequisites[i].length == 2

0 <= ai, bi < numCourses

ai != bi

所有[ai, bi] 互不相同

Related Topics

深度优先搜索

广度优先搜索

图

拓扑排序

解法一：

DFS

class Solution {
    boolean[] visited;
    boolean[] path;
    boolean hasCircle = false;
    ArrayList<Integer> logic = new ArrayList<>();

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        List<Integer>[] graph = build(numCourses, prerequisites);
        visited = new boolean[numCourses];
        path = new boolean[numCourses];

        for (int i = 0; i < numCourses; i++) {
            traverse(i, graph);
        }

        if (hasCircle) {
            return new int[0];
        }

        Collections.reverse(logic);
        return logic.stream().mapToInt(Integer::valueOf).toArray();
    }

    private List<Integer>[] build(int numCourses, int[][] prerequisites) {
        List<Integer>[] graph = new List[numCourses];
        for (int i = 0; i < numCourses; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] arr : prerequisites) {
            int to = arr[0];
            int from = arr[1];
            graph[from].add(to);
        }
        return graph;
    }

    private void traverse(int idx, List<Integer>[] graph) {
        if (path[idx]) {
            hasCircle = true;
            return;
        }

        if (hasCircle || visited[idx]) {
            return;
        }

        visited[idx] = true;
        path[idx] = true;
        for (int v : graph[idx]) {
            traverse(v, graph);
        }
        logic.add(idx);
        path[idx] = false;
    }
}

解法二：

BFS

通过出入度来判断一个结点是否可以被删除

class Solution {
    int[] indeg;

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        indeg = new int[numCourses];
        List<List<Integer>> graph = build(numCourses, prerequisites);
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < indeg.length; i++) {
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }

        int visited = 0;
        List<Integer> res = new ArrayList<>();
        while (!queue.isEmpty()) {
            visited++;
            Integer out = queue.poll();
            res.add(out);
            for (Integer i : graph.get(out)) {
                indeg[i]--;
                if (indeg[i] == 0) {
                    queue.offer(i);
                }
            }
        }

        return visited == numCourses ? res.stream().mapToInt(Integer::valueOf).toArray() : new int[0];
    }

    private List<List<Integer>> build(int numCourses, int[][] prerequisites) {
        List<List<Integer>> graph = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            graph.add(new ArrayList<Integer>());
        }

        for (int[] arr : prerequisites) {
            int from = arr[1];
            int to = arr[0];
            graph.get(from).add(to);
            indeg[to]++;
        }

        return graph;
    }
}

[213] 打家劫舍Ⅱ

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

示例 1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
  偷窃到的最高金额 = 1 + 3 = 4 。

示例 3：

输入：nums = [1,2,3]
输出：3

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 1000

Related Topics

数组

动态规划

解法一：

类似【打家劫舍Ⅰ】，把题目抽象成打两次，然后返回最大值即可

class Solution {
    public int rob(int[] nums) {
        if (nums.length == 1) {
            return nums[0];
        }

        return Math.max(rob(nums, 0, nums.length - 2), rob(nums, 1, nums.length - 1));
    }

    private int rob(int[] nums, int left, int right) {
        if (left == right) {
            return nums[left];
        }

        int[] dp = new int[right - left + 2];
        dp[0] = 0;
        dp[1] = nums[left];
        int max = dp[1];

        for(int i = 2; i < dp.length; i++) {
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i + left - 1]);
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}

[215] 数组中的第 K个最大整数

给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
提示：

1 <= k <= nums.length <= 104

-104 <= nums[i] <= 104

Related Topics

数组

分治

快速选择

排序

堆（优先队列）

解法一：

小根堆

class Solution {
    public int findKthLargest(int[] nums, int k) {
        // PriorityQueue是小根堆，也就是说堆顶元素最小
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for(int x : nums) {
            queue.offer(x);
            // 一旦队列中的元素数量超过了 k，那么就将队首(最小的元素)移除
            // 保证 queue存储 k个当前最大元素
            if (queue.size() > k) {
                queue.poll();
            }
        }
		// 因为是小根堆，所以队首就是第 k大的元素
        return queue.peek();
    }
}

解法二：

快排

class Solution {
    public int findKthLargest(int[] nums, int k) {
        // 打乱数组
        shuffle(nums);
        // 默认是从小到大排序的算法，要找第 k 大，就是找第 nums.length - K 小
        return KSort(nums, nums.length - k, 0, nums.length - 1);
    }

    private int KSort(int[] nums, int k, int left, int right) {

        while (left <= right) {
            // p返回的就是该元素在正确排序后数组中的位置
            int p =  partition(nums, left, right);
           
            if (p < k) {
                left = p + 1;
                continue;
            } else if (p > k) {
                right = p - 1;
                continue;
            }
            return nums[p];
        }
        return -1;
    }

    private int partition(int[] nums, int left, int right) {
        int pivot = left;
        int i = left, j = right;
        while(i <= j) {
            while(i < right && nums[i] <= nums[pivot]) {
                i++;
            }
            while(j > left && nums[j] > nums[pivot]) {
                j--;
            }
            if (i >= j) {
                break;
            }
            swap(nums, i, j);
        }
        swap(nums, pivot, j);
        return j;
    }

    private void shuffle(int[] nums) {
        Random random = new Random();
        for (int i = 0; i < nums.length; i++) {
            swap(nums, i, random.nextInt(nums.length));
        }
    }


    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

[220] 存在重复元素Ⅲ

给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j，使得 abs(nums[i] - nums[j]) <= t ，同时又满足 abs(i - j) <= k 。

如果存在则返回 true，不存在返回 false。

示例 1：
输入：nums = [1,2,3,1], k = 3, t = 0
输出：true
示例 2：
输入：nums = [1,0,1,1], k = 1, t = 2
输出：true
示例 3：
输入：nums = [1,5,9,1,5,9], k = 2, t = 3
输出：false
提示：

0 <= nums.length <= 2 * 104

-231 <= nums[i] <= 231 - 1

0 <= k <= 104

0 <= t <= 231 - 1

Related Topics

数组

桶排序

有序集合

排序

滑动窗口

解法一：

滑动窗口，并且使用有序集合存储

class Solution {
    public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        // 如果只用 HashSet的话，最后的一个测试用例会超时
        TreeSet<Long> window = new TreeSet<>();

        int left = 0, right = 0;
        while (right < nums.length) {
            int in = nums[right++];
            if (checkWindow(window, in, t)) {
                return true;
            }
            window.add((long)in);

            if (right > k) {
                int out = nums[left++];
                window.remove((long)out);
            }
        }

        return false;
    }

    private boolean checkWindow(TreeSet<Long> set, int in, int t) {
        Long ceil = set.ceiling((long)in);
        Long floor = set.floor((long)in);

        if (ceil != null && ceil - in <= t) return true;
        if (floor != null && in - floor <= t) return true;
        
        return false;
    }
}

[221] 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4
示例 2：
输入：matrix = [["0","1"],["1","0"]]
输出：1
示例 3：
输入：matrix = [["0"]]
输出：0
提示：

m == matrix.length

n == matrix[i].length

1 <= m, n <= 300

matrix[i][j] 为 '0' 或 '1'

Related Topics

数组

动态规划

矩阵

解法一：

dp[i][j]表示以 (i, j)为右下角的正方形的大小

class Solution {
    public int maximalSquare(char[][] matrix) {
        int[][] dp = new int[matrix.length + 1][matrix[0].length + 1];
        int max = 0;
        for(int i = 1; i <= matrix.length; i++) {
            for(int j = 1; j <= matrix[0].length; j++) {
                if (matrix[i - 1][j - 1] == '0') {
                    dp[i][j] = 0;
                    continue;
                }

                
                int len = (int) Math.sqrt(dp[i - 1][j - 1]);
                int idx = 1;
                for(int m = i - 2, n = j - 2; len > 0; len--) {
                    if(!(matrix[m--][j - 1] == '1' && matrix[i - 1][n--] == '1')) {
                        break;
                    }
                    idx++;
                }

                dp[i][j] = (int)Math.pow(idx, 2);
                max = Math.max(max, dp[i][j]);
            }
        }

        return max;
    }
}

优化一下，dp[i][j]记录以 (i, j)为右下角的正方形的边长

class Solution {
    public int maximalSquare(char[][] matrix) {
        int[][] dp = new int[matrix.length + 1][matrix[0].length + 1];
        int max = 0;
        for(int i = 1; i <= matrix.length; i++) {
            for(int j = 1; j <= matrix[0].length; j++) {
                if (matrix[i - 1][j - 1] == '0') {
                    dp[i][j] = 0;
                    continue;
                }
				// 获取三个数中最小的那一个
                dp[i][j] = 1 + getMin(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]);
                max = Math.max(max, dp[i][j]);
            }
        }

        return max * max;
    }

    private int getMin(int x, int y, int z) {
        return Math.min(x, Math.min(y, z));
    }
}

[222] 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：
输入：root = [1,2,3,4,5,6]
输出：6
示例 2：
输入：root = []
输出：0
示例 3：
输入：root = [1]
输出：1
提示：

树中节点的数目范围是[0, 5 * 104]

0 <= Node.val <= 5 * 104

题目数据保证输入的树是 完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

Related Topics

树

深度优先搜索

二分查找

二叉树

解法一：

无脑递归

递归全部节点，不考虑完全二叉树的特性

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }

        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

解法二：

递归+位运算

如果是满二叉树，可通过位运算 (1 << level) - 1计算二叉树的节点个数

因为题中给的是完全二叉树，所以左右子树中，肯定是有满二叉树的，可以直接获取层级后用位运算计算

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }

        int cnt = 0;

        // 计算左右子树的层级
        int leftLevel = countLevel(root.left);
        int rightLevel = countLevel(root.right);

        // 如果层级相等，表名左子树是满二叉树
        if (leftLevel == rightLevel) {
            // 之后对右子树递归
            cnt += (1 << leftLevel) + countNodes(root.right);
        } else {
            // 如果层级不相等，因为计算层级时都是取 left计算，因此，右子树肯定是满二叉树
            // 之后对左子树递归
            cnt += (1 << rightLevel) + countNodes(root.left);
        }

        return cnt;
    }

    /**
    * 计算树的最大层级（仅限完全二叉树）
    */
    public int countLevel(TreeNode root) {
        int level = 0;
        while (root != null) {
            root = root.left;
            level++;
        }

        return level;
    }

}

非递归版本：

class Solution {
    public int countNodes(TreeNode root) {
        int cnt = 0;

        while (root != null) {
            int leftLevel = countLevel(root.left);
            int rightLevel = countLevel(root.right);

            if (leftLevel == rightLevel) {
                cnt += (1 << leftLevel);
                root = root.right;
            } else {
                cnt += (1 << rightLevel);
                root = root.left;
            }
        }

        return cnt;
    }

    public int countLevel(TreeNode root) {
        int level = 0;
        while (root != null) {
            root = root.left;
            level++;
        }

        return level;
    }

}

第二次手写

class Solution {
    // 和上面的递归版本的区别在于，递归版本每次传入的是 root.left 和 root.right，那么它得到的其实是两颗子树的分别的高度
    // 因此最多只能保证左子树是满的(两种写法的 countLevel不一样的)
    // 而当前写法，可以直接判断本二叉树是不是满二叉树
    public int countNodes(TreeNode root) {

        if (root == null) {
            return 0;
        }
        
        int l = getLeftDepth(root);
        int r = getRightDefth(root);

        if (l == r) {
            return (int)Math.pow(2, l) - 1;
        }

        return 1 + countNodes(root.left) + countNodes(root.right);
    }

    private int getLeftDepth(TreeNode root) {
        int l = 0;
        while(root != null) {
            l++;
            root = root.left;
        }
        return l;
    }

    private int getRightDefth(TreeNode root) {
        int r = 0;
        while(root != null) {
            r++;
            root = root.right;
        }
        return r;
    } 
}

[230] 二叉搜索树中第 K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：
输入：root = [3,1,4,null,2], k = 1
输出：1
示例 2：
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3
提示：

树中的节点数为 n 。

1 <= k <= n <= 104

0 <= Node.val <= 104

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

Related Topics

树

深度优先搜索

二叉搜索树

二叉树

解法一：

中序遍历

每一次遍历都更新当前节点是第几个节点，如果等于 k，就返回

class Solution {
    // 结果值
    int res = 0;
    // 要找第几个，就是 k
    int cnt;
    // 现在是第几个
    int idx = 0;

    public int kthSmallest(TreeNode root, int k) {
        cnt = k;
        traverse(root);
        return res;
    }

    private void traverse(TreeNode root) {
        // base condition
        if (root == null) {
            return;
        }

        // 中序遍历
        traverse(root.left);
        
        // 判断是否需要返回
        if (++idx == cnt) {
            res = root.val;
            return;
        }

        traverse(root.right);
    }
}

解法二：

自定义数据结构，构造 AVL树，太麻烦了，没看懂

[236] 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2：
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3：
输入：root = [1,2], p = 1, q = 2
输出：1
提示：

树中节点数目在范围 [2, 105] 内。

-109 <= Node.val <= 109

所有 Node.val 互不相同 。

p != q

p 和 q 均存在于给定的二叉树中。

Related Topics

树

深度优先搜索

二叉树

解法一：

判断 root.val == p.val || root.val == q.val

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return find(root, p, q);
    }

    private TreeNode find(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }

        // 说明当前 root就是 p，q中的一个
        if (root.val == p.val || root.val == q.val) {
            return root;
        }

        TreeNode left = find(root.left, p, q);
        TreeNode right = find(root.right, p, q);
        
        // 关键
        // 下面两步 return很关键，如果当前子树中有结果，保证把这个结果传上去！！
        if (left != null && right != null) {
            return root;
        }

        return left == null ? right : left;
    }
}

[237] 删除链表中的节点

请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点。传入函数的唯一参数为 要被删除的节点 。

现有一个链表 -- head = [4,5,1,9]，它可以表示为:

示例 1：
输入：head = [4,5,1,9], node = 5
输出：[4,1,9]
解释：给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.
示例 2：
输入：head = [4,5,1,9], node = 1
输出：[4,5,9]
解释：给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.
提示：

链表至少包含两个节点。

链表中所有节点的值都是唯一的。

给定的节点为非末尾节点并且一定是链表中的一个有效节点。

不要从你的函数中返回任何结果。

Related Topics

链表

解法一：

这里只传入了一个结点（待删除的节点），我们没有办法获取它的前驱节点

题目中又说：给定节点为非末尾节点

所以采取的措施是：把后继节点的 val取过来，然后再把后驱节点干掉！

（什么沙雕题目）

class Solution {
    public void deleteNode(ListNode node) {
        node.val = node.next.val;
        node.next = node.next.next;
    }
}

[238] 除自身以外数组的乘积

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示：

2 <= nums.length <= 105

-30 <= nums[i] <= 30

保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内

进阶：你可以在 O(1) 的额外空间复杂度内完成这个题目吗？（出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

Related Topics

数组

前缀和

解法一：

先用除法实现

class Solution {
    public int[] productExceptSelf(int[] nums) {

        int[] res = new int[nums.length];
        int total = 1;
        int zeroCnt = 0;
        
        // 统计 0的数量
        for(int x : nums) {
            if (x==0) {
                zeroCnt++;
                continue;
            }
            total *= x;
        }

        // 根据 0的个数情况做不同的处理
        if(zeroCnt == 0) {
            for(int i = 0; i < nums.length; i++) {
                res[i] = total / nums[i];
            }
        } else if (zeroCnt == 1) {
           for(int i = 0; i < nums.length; i++) {
                res[i] = nums[i] == 0 ? total : 0;
            } 
        }

        return res;

    }
}

解法二：

左右乘积列表

设置两个前缀和数组，分别存储从 0 ~ i 和 i+1 ~ nums.length的元素乘积，到时候就 arr1[i] * arr2[i]即可

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] left = new int[nums.length];
        int[] right = new int[nums.length];
        int[] res = new int[nums.length];

        left[0] = 1;
        right[nums.length - 1] = 1;

        for(int i = 1; i < nums.length; i++) {
            left[i] = left[i-1] * nums[i-1];
        }

        for(int i = nums.length - 2; i >= 0; i--) {
            right[i] = right[i+1] * nums[i+1];
        }

        for(int i = 0; i<nums.length; i++) {
            res[i] = left[i] * right[i];
        }

        return res;

    }
}

解法三：

先把 res数组当作 left来用，然后从后向前遍历 nums数组并类乘值，顺便把 res乘上，就实现了空间 O(1)

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] res = new int[nums.length];
        res[0] = 1;

        // 先当作 left来使用
        for(int i = 1; i < nums.length; i++) {
            res[i] = res[i-1] * nums[i-1];
        }

        // 统计 right，顺便把 res也乘好，注意其实此时 res[length - 1]已经不需要再乘了
        int right = 1;
        for(int i = nums.length - 2; i >= 0; i--) {
            right = right * nums[i + 1];
            res[i] = right * res[i];
        }

        return res;
    }
}

[240] 搜索二维矩阵Ⅱ

编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
示例 2：
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false
提示：

m == matrix.length

n == matrix[i].length

1 <= n, m <= 300

-109 <= matrix[i][j] <= 109

每行的所有元素从左到右升序排列

每列的所有元素从上到下升序排列

-109 <= target <= 109

Related Topics

数组

二分查找

分治

矩阵

解法一：

从右上角开始遍历，大的向下，小的向左

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = 0, col = matrix[0].length - 1;
        
        while (row < matrix.length && col >= 0) {
            if (matrix[row][col] == target) {
                return true;
            } else if (matrix[row][col] > target) {
                col--;
            } else {
                row++;
            }
        }

        return false;
    }
}

[253] 会议室Ⅱ

给你一个会议时间安排的数组 intervals ，每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ，返回 所需会议室的最小数量 。

示例 1：
输入：intervals = [[0,30],[5,10],[15,20]]
输出：2
示例 2：
输入：intervals = [[7,10],[2,4]]
输出：1
提示：

1 <= intervals.length <= 104

0 <= starti < endi <= 106

Related Topics

贪心

数组

双指针

排序

堆（优先队列）

解法一：

扫描线

将会议的开始和结束时间投影到x轴，然后逐个判断

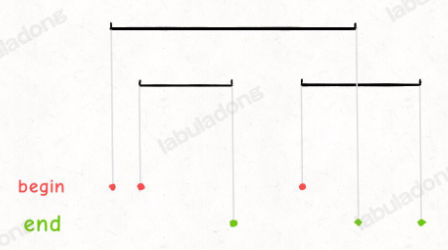
class Solution {
    public int minMeetingRooms(int[][] intervals) {
        int[] begin = new int[intervals.length];
        int[] end = new int[intervals.length];

		// 将开始和结束时间分别统计
        for(int i = 0; i < intervals.length; i++) {
            begin[i] = intervals[i][0];
            end[i] = intervals[i][1];
        }

        // 排序，便于之后做判断
        Arrays.sort(begin);
        Arrays.sort(end);

        int cnt = 0;
        int res = 0;
        int i = 0, j = 0;
        while (i < begin.length && j < end.length) {
            if (begin[i] < end[j]) {
                cnt++;
                i++;
            } else {
                cnt--;
                j++;
            }
            res = Math.max(res, cnt);
        }
        return res;
    }
}

[279] 完全平方数

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：
输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4
示例 2：
输入：n = 13
输出：2
解释：13 = 4 + 9
提示：

1 <= n <= 104

Related Topics

广度优先搜索

数学

动态规划

解法一：

dp[i] 表示数 i 的完全平方数的最少数量，那么 dp[i] = 1 + min(dp[i - j*j]) | 1 <= j <= sqrt(i);

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];

        for(int i = 1; i <= n; i++) {
            int min = Integer.MAX_VALUE;
            
            for(int j = 1; j * j <= i; j++) {
                min = Math.min(min, dp[i - j*j]);
            }
            dp[i] = min + 1;
        }

        return dp[n];
        
    }
}

[287] 寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：
输入：nums = [1,3,4,2,2]
输出：2
示例 2：
输入：nums = [3,1,3,4,2]
输出：3
提示：

1 <= n <= 105

nums.length == n + 1

1 <= nums[i] <= n

nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现一次

进阶：

如何证明 nums 中至少存在一个重复的数字?

你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

Related Topics

位运算

数组

双指针

二分查找

解法一：

快慢指针

当作环形链表找起始点拿到题来看，一开始一个走一步，另一个走两步，因为有重复，所以一定会相遇！

然后一个回到 0，双方慢慢走，最后走到的就是重复点

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = 0, fast = 0;
        
        // slow 走 1步，fast走两步
        do {
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while (slow != fast);

        // slow回到 0，大家都走 1步
        slow = 0;
        while(slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }

        return slow;
    }
}

[300] 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
示例 2：
输入：nums = [0,1,0,3,2,3]
输出：4
示例 3：
输入：nums = [7,7,7,7,7,7,7]
输出：1
提示：

1 <= nums.length <= 2500

-104 <= nums[i] <= 104

进阶：

你可以设计时间复杂度为 O(n2) 的解决方案吗？

你能将算法的时间复杂度降低到 O(n log(n)) 吗?

Related Topics

数组

二分查找

动态规划

解法一：

构建数组 int[] dp，用来记录每个以 nums[i]结尾的最长序列

最后遍历 dp[]数组，获取存储的最大的值

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length + 1];
        // 每个序列至少包涵一个结尾的字符，所以至少是 1
        Arrays.fill(dp, 1);
        
        // O(N)
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
        
        // 找到最大的数
        int res = 1;
        for (int i : dp) {
            res = Math.max(res, i);
        }

        return res;
    }
}

[304] 二维区域和检索 - 矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和。

示例 1：

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-105 <= matrix[i][j] <= 105
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 104 次 sumRegion 方法

Related Topics

设计

数组

矩阵

前缀和

解法一：

对每一行计算单行的前缀和

针对矩阵中的每一行计算前缀和，在计算子矩阵元素和时，也同样逐行求和，最后再统一相加。

因此，还是 O(N)

class NumMatrix {

    int[][] preSum; // 前缀矩阵
    int rowLen; // 行数
    int colLen; //列数

    public NumMatrix(int[][] matrix) {
        rowLen = matrix.length;
        colLen = matrix[0].length;

        preSum = new int[rowLen][colLen + 1]; // 列数 + 1是为了方便第一个前缀的计算

        // 构造前缀矩阵，每一行构造一次
        for (int i = 0; i < rowLen; i++) {
            for (int j = 1; j < colLen + 1; j++) {
                // 前缀数组中的当前元素的值 = 当前 matrix数组中的元素 + 前缀数组中的上一个元素
                preSum[i][j] = preSum[i][j - 1] + matrix[i][j - 1];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        // 按行遍历
        for (int i = row1; i <= row2; i++) {
            sum += (preSum[i][col2 + 1] - preSum[i][col1]);
        }
        return sum;
    }
}

解法二：对一个二维矩阵整体计算前缀和

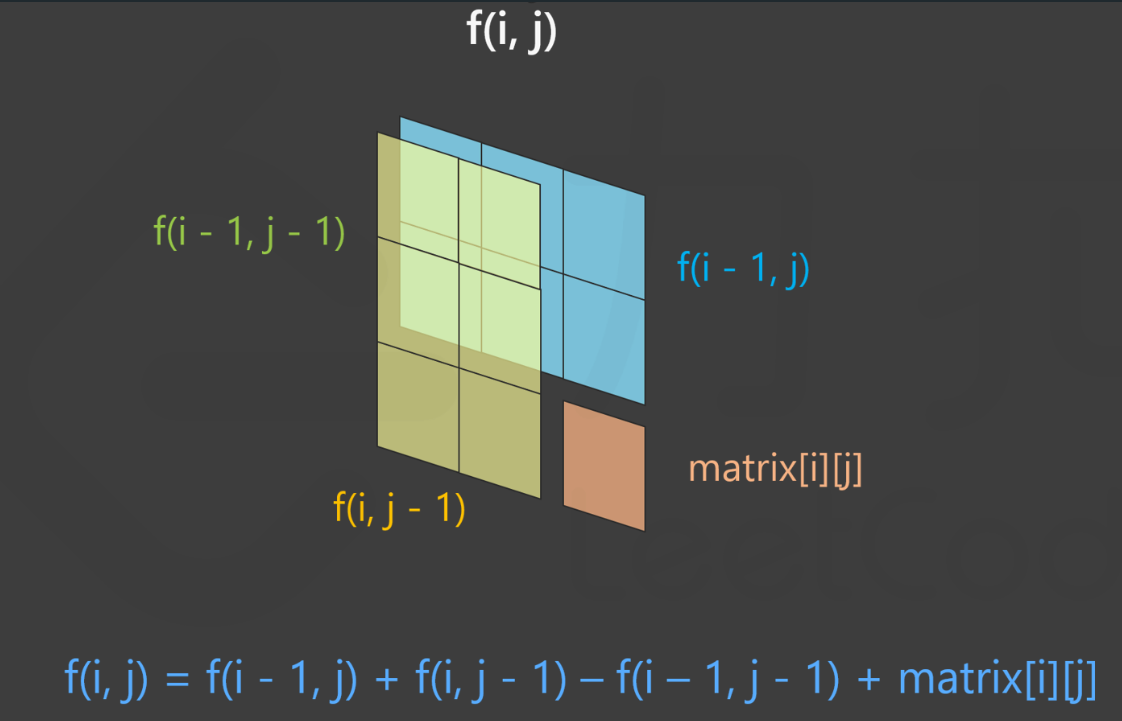
注意上图中的表达式：preSum[i][j]表示的是长为 i，宽为 j 的矩形的前缀和

而在计算某一个子矩阵和时，可采用如下表达式：

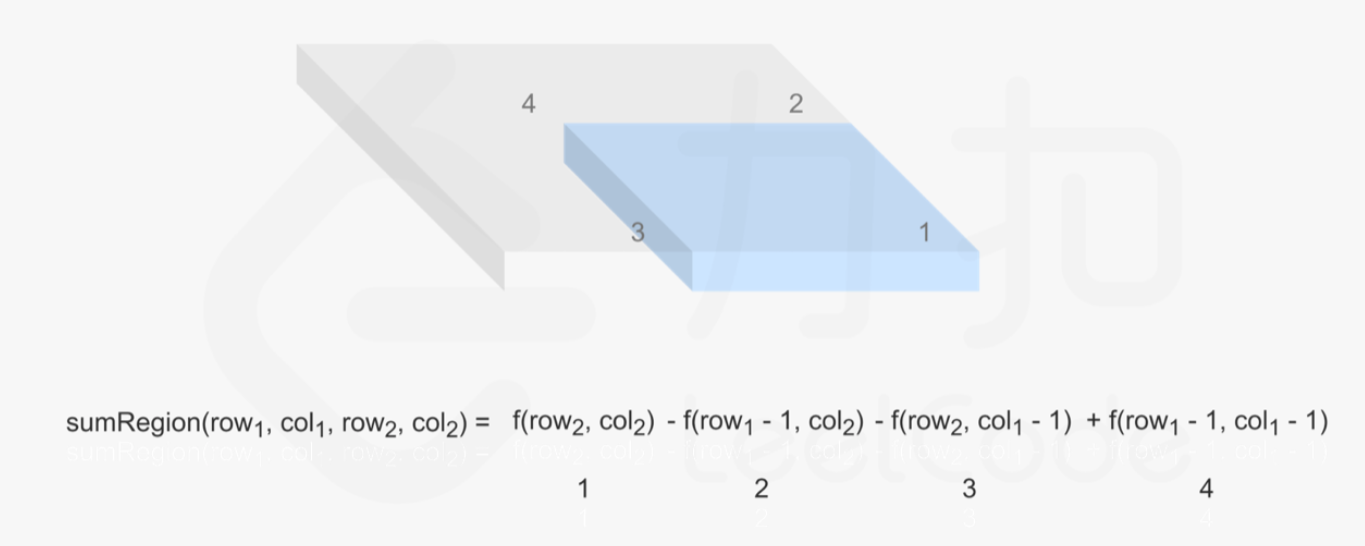
class NumMatrix {
    int[][] preSum; // 定义二维的前缀和数组
    int rowLen; // 长度
    int colLen; // 宽度

    public NumMatrix(int[][] matrix) {
        this.rowLen = matrix.length;
        this.colLen = matrix[0].length;
        preSum = new int[rowLen + 1][colLen + 1]; // 长和宽都要 + 1，边界上的点的计算 

        // 构建二维的前缀和数组
        for (int i = 1; i < rowLen + 1; i++) {
            for (int j = 1; j < colLen + 1; j++) {
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
            }
        }
    }

  
    public int sumRegion(int row1, int col1, int row2, int col2) {
        // O(1)直接获取值，真帅啊
        return preSum[row2 + 1][col2 + 1] + preSum[row1][col1] - preSum[row2 + 1][col1] - preSum[row1][col2 + 1];
    }
}

[309] 最佳股票买卖时机含冷冻期

给定一个整数数组prices，其中第 prices[i] 表示第 *i* 天的股票价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:
输入: prices = [1,2,3,0,2]
输出: 3 
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
输入: prices = [1]
输出: 0
提示：

1 <= prices.length <= 5000

0 <= prices[i] <= 1000

Related Topics

数组

动态规划

解法一：

压缩空间后的解法

class Solution {
    public int maxProfit(int[] prices) {
        int buy = Integer.MIN_VALUE;
        int sell = 0, last_sell = 0;

        for(int x : prices) {
            buy = Math.max(buy, last_sell - x);
            last_sell = sell;
            sell = Math.max(sell, buy + x);
        }

        return sell;
    }
}

[316] 去除重复字母

给你一个字符串 s ，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证 返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

示例 1：
输入：s = "bcabc"
输出："abc"
示例 2：
输入：s = "cbacdcbc"
输出："acdb"
提示：

1 <= s.length <= 104

s 由小写英文字母组成

注意：该题与 1081 https://leetcode-cn.com/problems/smallest-subsequence-of-distinct-characters 相同

Related Topics

栈

贪心

字符串

单调栈

解法一：

单调栈

class Solution {
    public String removeDuplicateLetters(String s) {
        // 记录字符出现的次数
        int[] word = new int[26];
        char[] arr = s.toCharArray();
        for (char c : arr) {
            word[c - 'a']++;
        }

        // 构造单调栈
        Stack<Character> stack = new Stack<>();
        for (char c : arr) {
            word[c - 'a']--;
            // 如果栈中已存在数据就跳过入栈
            if (stack.contains(c)) {
                continue;
            }
            // 把后续存在重复 且 ASCII码值更大的弹栈，让个儿小的先钻进去
            while (!stack.isEmpty()
                    && word[stack.peek() - 'a'] > 0
                    && stack.peek() > c) {
                stack.pop();
            }
            stack.push(c);
        }

        // 构造返回的字符串
        for (int i = 0; i < stack.size(); i++) {
            arr[i] = stack.get(i);
        }
        return new String(arr, 0, stack.size());
    }
}

[322] 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：
输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1
示例 2：
输入：coins = [2], amount = 3
输出：-1
示例 3：
输入：coins = [1], amount = 0
输出：0
示例 4：
输入：coins = [1], amount = 1
输出：1
示例 5：
输入：coins = [1], amount = 2
输出：2
提示：

1 <= coins.length <= 12

1 <= coins[i] <= 231 - 1

0 <= amount <= 104

Related Topics

广度优先搜索

数组

动态规划

解法一：

建立数组 dp[amount + 1]，dp[i]就表示凑到 i元钱对应的最少硬币个数

通过题干可得到 状态转移方程

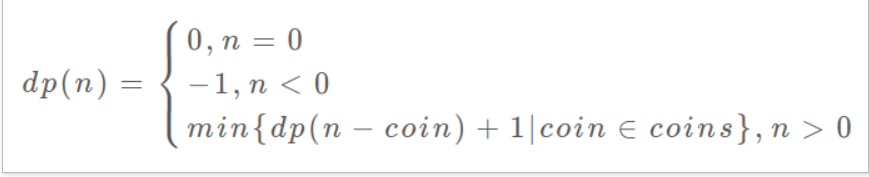
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        
        for (int i = 0; i < dp.length; i++) {
            for (int coin : coins) {
                // 如果要求的钱小于硬币的面值，就跳过
                if (i - coin < 0) {
                    continue;
                }
				// 其实针对 dp[i] ，会有多次变化，但是每次变化时存储的都是需要硬币更少的那一个
                dp[i] = Math.min(dp[i - coin] + 1, dp[i]);
            }
        }

        return dp[amount] == amount + 1 ? -1 : dp[amount];
    }
}

[337] 打家劫舍Ⅲ

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额。

示例 1:
输入: root = [3,2,3,null,3,null,1]
输出: 7 
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
提示：

树的节点数在 [1, 104] 范围内

0 <= Node.val <= 104

Related Topics

树

深度优先搜索

动态规划

二叉树

解法一：

类似打家劫舍的一和二，

如果打劫了当前 root，那么下一次最多只能打孙子节点的数据了；

如果不打劫 root，那么下一次可以打儿子节点

class Solution {
    Map<TreeNode, Integer> dp = new HashMap<>();
    
    public int rob(TreeNode root) {
        traverse(root);
        return dp.get(root);
    }

    private int traverse(TreeNode root) {
        if (root == null) {
            return 0;
        }

        if (dp.containsKey(root)) {
            return dp.get(root);
        }

        int rob_root = root.val + 
            (root.left == null ? 0 : (traverse(root.left.left) + traverse(root.left.right))) +
            (root.right == null ? 0 :(traverse(root.right.left) + traverse(root.right.right)));

        int no_rob_root = traverse(root.left) + traverse(root.right);

        int res = Math.max(rob_root, no_rob_root);
        dp.put(root, res);
        return res;

    }
}

解法二：

本质上差不多，但优化了对孙节点的访问

class Solution {
    public int rob(TreeNode root) {
        // 0表示打劫了 root，1表示没打劫 root
        int[] res = traverse(root);
        return Math.max(res[0], res[1]);
    }

    private int[] traverse(TreeNode root) {
        if (root == null) {
            return new int[]{0, 0};
        }

        int[] left = traverse(root.left);
        int[] right = traverse(root.right);

        // 如果打劫了 root，那就打劫孙子
        int rob_root = root.val + left[1] + right[1];
        // 如果没打劫 root，那打劫孙子和儿子都可以
        int no_rob_root =Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        
        return new int[]{rob_root, no_rob_root};
    }
}

[341] 扁平化嵌套列表迭代器

给你一个嵌套的整数列表 nestedList 。每个元素要么是一个整数，要么是一个列表；该列表的元素也可能是整数或者是其他列表。请你实现一个迭代器将其扁平化，使之能够遍历这个列表中的所有整数。

// This is the interface that allows for creating nested lists.
// You should not implement it, or speculate about its implementation
public interface NestedInteger {
    // @return true if this NestedInteger holds a single integer, rather than a nested list.
    public boolean isInteger();
    
    // @return the single integer that this NestedInteger holds, if it holds a single integer
    // Return null if this NestedInteger holds a nested list
    public Integer getInteger();

    // @return the nested list that this NestedInteger holds, if it holds a nested list
    // Return empty list if this NestedInteger holds a single integer
    public List<NestedInteger> getList();
}

实现扁平迭代器类 NestedIterator ：

NestedIterator(List<NestedInteger> nestedList) 用嵌套列表 nestedList 初始化迭代器。
int next() 返回嵌套列表的下一个整数。
boolean hasNext() 如果仍然存在待迭代的整数，返回 true ；否则，返回 false 。

你的代码将会用下述伪代码检测：

initialize iterator with nestedList
res = []
while iterator.hasNext()
    append iterator.next() to the end of res
return res

如果 res 与预期的扁平化列表匹配，那么你的代码将会被判为正确。

示例 1：
输入：nestedList = [[1,1],2,[1,1]]
输出：[1,1,2,1,1]
解释：通过重复调用 next 直到 hasNext 返回 false，next 返回的元素的顺序应该是: [1,1,2,1,1]。
示例 2：
输入：nestedList = [1,[4,[6]]]
输出：[1,4,6]
解释：通过重复调用 next 直到 hasNext 返回 false，next 返回的元素的顺序应该是: [1,4,6]。
提示：

1 <= nestedList.length <= 500

嵌套列表中的整数值在范围 [-106, 106] 内

Related Topics

栈

树

深度优先搜索

设计

队列

迭代器

解法一：

一次性将所有数据全都展开

public class NestedIterator implements Iterator<Integer> {
	// 承载所有数字
    Iterator<Integer> res;

    public NestedIterator(List<NestedInteger> nestedList) {
        List<Integer> list = new ArrayList<>();
        for (NestedInteger o : nestedList) {
            traverse(o, list);
        }

        this.res = list.iterator();
    }

    // 递归展开所有数据
    private void traverse(NestedInteger i, List<Integer> list) {
        if (i.isInteger()) {
            list.add(i.getInteger());
        } else {
            for (NestedInteger o : i.getList()) {
                traverse(o, list);
            }
        }
    }

    @Override
    public Integer next() {
        return res.next();
    }

    @Override
    public boolean hasNext() {
        return res.hasNext();
    }
}

第二次手写

public class NestedIterator implements Iterator<Integer> {

    List<Integer> res = new LinkedList<>();
    int idx = 0;

    public NestedIterator(List<NestedInteger> nestedList) {
        traverse(nestedList, 0);
    }

    private void traverse(List<NestedInteger> nestedList, int i) {
        if (i >= nestedList.size()) {
            return;
        }
        NestedInteger ni = nestedList.get(i);
        if (ni.isInteger()) {
            res.add(ni.getInteger());
            traverse(nestedList, i+1);
            return;
        }

        traverse(ni.getList(), 0);
        traverse(nestedList, i+1);
    }

    @Override
    public Integer next() {
        return res.get(idx++);
    }

    @Override
    public boolean hasNext() {
       return idx < res.size();
    }
}

解法二：

先不展开，到需要用的时候再展开

public class NestedIterator implements Iterator<Integer> {
    LinkedList<NestedInteger> res;

    public NestedIterator(List<NestedInteger> nestedList) {
        // 直接塞进去
        res = new LinkedList<>(nestedList);
    }

    @Override
    public Integer next() {
        // 直接弹出来
        return res.pollFirst().getInteger();
    }

    @Override
    public boolean hasNext() {
        // 获取第一个元素，如果是列表就扁平化
        // 存在空列表作为 NestedInteger的特殊情况，所以需要循环
        while (!res.isEmpty() && !res.peek().isInteger()) {
            List<NestedInteger> list = res.pollFirst().getList();
            for (int i = 0; i < list.size(); i++) {
                res.add(i, list.get(i));
            }
        }
        return !res.isEmpty();
    }
}

[347] 前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示：

1 <= nums.length <= 105

k 的取值范围是 [1, 数组中不相同的元素的个数]

题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

进阶：你所设计算法的时间复杂度必须优于 O(n log n) ，其中 n 是数组大小。

Related Topics

数组

哈希表

分治

桶排序

计数

快速选择

排序

堆（优先队列）

解法一：

优先级队列，堆排序

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 计算频率
        Map<Integer, Integer> val_freq = new HashMap<>();
        for(int x : nums) {
            val_freq.put(x, val_freq.getOrDefault(x, 0) + 1);
        }
		
        // 小根堆，维持前 K高频的数
        PriorityQueue<Integer> queue = new PriorityQueue<>((o1, o2)->{
            return val_freq.get(o1) - val_freq.get(o2);
        });
        
        for(int x : val_freq.keySet()) {
            queue.offer(x);
            if (queue.size() > k) {
                queue.poll();
            }
        }

        int[] res = new int[k];
        for(int i = 0; i < k; i++) {
            res[i] = queue.poll();
        }
        return res;
    }
}

[370] 区间加法

假设你有一个长度为 n 的数组，初始情况下所有的数字均为 0，你将会被给出 k** 个更新的操作。

其中，每个操作会被表示为一个三元组：[startIndex, endIndex, inc]，你需要将子数组 A[startIndex ... endIndex]（包括 startIndex 和 endIndex）增加 inc。

请你返回 *k* 次操作后的数组。

示例:

输入: length = 5, updates = [[1,3,2],[2,4,3],[0,2,-2]]
输出: [-2,0,3,5,3]

解释:

初始状态:
[0,0,0,0,0]

进行了操作 [1,3,2] 后的状态:
[0,2,2,2,0]

进行了操作 [2,4,3] 后的状态:
[0,2,5,5,3]

进行了操作 [0,2,-2] 后的状态:
[-2,0,3,5,3]

Related Topics

数组

前缀和

解法一：

前缀和的变式——差分数组；

前缀和是从 0加到 i，得到一个数组；

差分数组是第i个数 - 第i-1个数，得到一个数组；便于频繁的区间内数的加减；

class Solution {
    public int[] getModifiedArray(int length, int[][] updates) {
        // 因为一开始都是 0，所以 arr就已经是差分数组了
        int[] arr = new int[length];

        for(int[] up : updates) {
            arr[up[0]] += up[2];
            if (up[1] < arr.length - 1) 
                arr[up[1] + 1] -= up[2];
        }
		// 差分数组的恢复，因为原来的数都是 0，所以可以直接在 arr上操作
        for(int i = 1; i<arr.length; i++) {
            arr[i] += arr[i-1];
        }


        return arr;
    }
}

[380] O(1) 时间插入、删除和获取随机元素

实现RandomizedSet 类：

RandomizedSet() 初始化 RandomizedSet 对象
bool insert(int val) 当元素 val 不存在时，向集合中插入该项，并返回 true ；否则，返回 false 。
bool remove(int val) 当元素 val 存在时，从集合中移除该项，并返回 true ；否则，返回 false 。
int getRandom() 随机返回现有集合中的一项（测试用例保证调用此方法时集合中至少存在一个元素）。每个元素应该有 相同的概率 被返回。

你必须实现类的所有函数，并满足每个函数的平均时间复杂度为 O(1) 。

示例：

输入
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
输出
[null, true, false, true, 2, true, false, 2]

解释
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // 向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomizedSet.remove(2); // 返回 false ，表示集合中不存在 2 。
randomizedSet.insert(2); // 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。
randomizedSet.getRandom(); // getRandom 应随机返回 1 或 2 。
randomizedSet.remove(1); // 从集合中移除 1 ，返回 true 。集合现在包含 [2] 。
randomizedSet.insert(2); // 2 已在集合中，所以返回 false 。
randomizedSet.getRandom(); // 由于 2 是集合中唯一的数字，getRandom 总是返回 2 。

提示：

-231 <= val <= 231 - 1
最多调用 insert、remove 和 getRandom 函数 2 * ``105 次
在调用 getRandom 方法时，数据结构中 至少存在一个 元素。

Related Topics

设计

数组

哈希表

数学

随机化

解法一：

哈希表

class RandomizedSet {
	// 存储数据
    LinkedList<Integer> value;
    // 存数据和下标，保证 O(1)删除
    HashMap<Integer, Integer> valToIndex;
    Random random;

    public RandomizedSet() {
        value = new LinkedList<>();
        valToIndex = new HashMap<>();
        random = new Random();
    }

    public boolean insert(int val) {
        if (valToIndex.containsKey(val)) {
            return false;
        }
        valToIndex.put(val, value.size());
        value.addLast(val);

        return true;
    }

    public boolean remove(int val) {

        if (!valToIndex.containsKey(val)) {
            return false;
        }

        Integer lastVal = value.getLast();
        Integer valIdx = valToIndex.get(val);

        value.set(valIdx, lastVal);
        value.removeLast();

        valToIndex.put(lastVal, valIdx);
        valToIndex.remove(val);
        return true;
    }

    public int getRandom() {
        int idx = random.nextInt(value.size());
        return value.get(idx);
    }
}

第二遍手写

class RandomizedSet {

    HashMap<Integer, Integer> MAP_VAL_IDX;
    LinkedList<Integer> LIST_VAL;
    Random random;

    public RandomizedSet() {
        MAP_VAL_IDX = new HashMap<>();
        LIST_VAL = new LinkedList<>();
        random = new Random();
    }
    
    public boolean insert(int val) {
        if (MAP_VAL_IDX.containsKey(val)) {
            return false;
        }
        MAP_VAL_IDX.put(val, LIST_VAL.size());
        LIST_VAL.add(val);
        return true;
    }
    
    public boolean remove(int val) {
        if (!MAP_VAL_IDX.containsKey(val)) {
            return false;
        }
        
        // 为了实现 O(1)的删除，必须将待删除的元素和最后一个元素互换位置，然后再删除最后一个
        int delIdx = MAP_VAL_IDX.remove(val);
        int lastVal = LIST_VAL.getLast();
        if (lastVal != val) {
            MAP_VAL_IDX.put(lastVal, delIdx);
        }

        LIST_VAL.set(delIdx, lastVal);
        LIST_VAL.removeLast();
        return true;

    }
    
    public int getRandom() {
        int idx = random.nextInt(LIST_VAL.size());
        return LIST_VAL.get(idx);
    }
}

[382] 链表随机节点

给你一个单链表，随机选择链表的一个节点，并返回相应的节点值。每个节点 被选中的概率一样 。

实现 Solution 类：

Solution(ListNode head) 使用整数数组初始化对象。
int getRandom() 从链表中随机选择一个节点并返回该节点的值。链表中所有节点被选中的概率相等。

示例：
输入
["Solution", "getRandom", "getRandom", "getRandom", "getRandom", "getRandom"]
[[[1, 2, 3]], [], [], [], [], []]
输出
[null, 1, 3, 2, 2, 3]
解释
Solution solution = new Solution([1, 2, 3]);
solution.getRandom(); // 返回 1
solution.getRandom(); // 返回 3
solution.getRandom(); // 返回 2
solution.getRandom(); // 返回 2
solution.getRandom(); // 返回 3
// getRandom() 方法应随机返回 1、2、3中的一个，每个元素被返回的概率相等。
提示：

链表中的节点数在范围 [1, 104] 内

-104 <= Node.val <= 104

至多调用 getRandom 方法 104 次

进阶：

如果链表非常大且长度未知，该怎么处理？

你能否在不使用额外空间的情况下解决此问题？

Related Topics

水塘抽样

链表

数学

随机化

解法一：

初始化时就暂存所有节点的值

class Solution {

    List<Integer> list;
    Random random;

    public Solution(ListNode head) {
        list = new LinkedList<>();
        random = new Random();
        while(head != null) {
            list.add(head.val);
            head = head.next;
        }
    }
    
    public int getRandom() {
        int targetIdx = random.nextInt(list.size());
        return list.get(targetIdx);
    }
}

解法二：

水塘抽样

针对未知长度的样本，求其概率

class Solution {

    ListNode head;
    Random random;

    public Solution(ListNode head) {
        this.head = head;
        random = new Random();
    }
    
    public int getRandom() {
        // 注意这里一定要先把 head赋值到局部变量里，因为 getRandom会调用多次
        ListNode node = head;
        int idx = 1, res = 0;
        while (node != null) {
            if (random.nextInt(idx) == 0) {
                res = node.val;
            }
            idx++;
            node = node.next;
        }
        return res;
    }
}

[384] 打乱数组

给你一个整数数组 nums ，设计算法来打乱一个没有重复元素的数组。

实现 Solution class:

Solution(int[] nums) 使用整数数组 nums 初始化对象
int[] reset() 重设数组到它的初始状态并返回
int[] shuffle() 返回数组随机打乱后的结果

示例：

输入
["Solution", "shuffle", "reset", "shuffle"]
[[[1, 2, 3]], [], [], []]
输出
[null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]

解释
Solution solution = new Solution([1, 2, 3]);
solution.shuffle();    // 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。例如，返回 [3, 1, 2]
solution.reset();      // 重设数组到它的初始状态 [1, 2, 3] 。返回 [1, 2, 3]
solution.shuffle();    // 随机返回数组 [1, 2, 3] 打乱后的结果。例如，返回 [1, 3, 2]

提示：

1 <= nums.length <= 200
-106 <= nums[i] <= 106
nums 中的所有元素都是 唯一的
最多可以调用 5 * 104 次 reset 和 shuffle

Related Topics

数组

数学

随机化

解法一：

shuffle()过程遍历整个数组，随机元素交换

实际上，没有太了解题目

class Solution {

    private int[] arr;
    private Random random;

    public Solution(int[] nums) {
        arr = nums;
        random = new Random(arr.length);
    }

    public int[] reset() {
        return arr;
    }

    public int[] shuffle() {
        if (arr == null) {
            return arr;
        }

        // 不能直接在 arr上进行修改，否则就回不去了
        int[] clone = arr.clone();

        for (int i = 1; i < clone.length; i++) {
            int j = random.nextInt(i + 1);
            swap(clone, i, j);
        }
        return clone;
    }

    private void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

[394] 字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

示例 1：
输入：s = "3[a]2[bc]"
输出："aaabcbc"
示例 2：
输入：s = "3[a2[c]]"
输出："accaccacc"
示例 3：
输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"
示例 4：
输入：s = "abc3[cd]xyz"
输出："abccdcdcdxyz"
提示：

1 <= s.length <= 30

s 由小写英文字母、数字和方括号 '[]' 组成

s 保证是一个有效的输入。

s 中所有整数的取值范围为 [1, 300]

Related Topics

栈

递归

字符串

解法一：

两个栈，一个存数字，一个存被嵌套时的外面的值

class Solution {
    public String decodeString(String s) {

        // 记录距今为止计算得到的值
        StringBuilder sb = new StringBuilder();
        // 临时记录针对之后的字符串需要重复几次
        int v = 0;
        // 因为有可能嵌套，所以 v 可能会被覆盖，那么就每次都用栈记录下重复的次数
        Stack<Integer> multi_val = new Stack<>();
        // 主要是针对嵌套情况，用于记录外面的字符串
        Stack<String> multi_char = new Stack<>();

        for(char x : s.toCharArray()) {
            // 如果遇到了 [，说明次数 v 已经计算完了，那么就把 v 放入到数字栈中
            if (x == '[') {
                multi_val.push(v);
                // 考虑到当前 [] 可能是内嵌的部分，此时需要把外层的字符串放到栈中暂存
                multi_char.push(sb.toString());
                v = 0;
                sb = new StringBuilder();
            } else if (x == ']') {
                // 获取要循环的次数，这指的是对 sb的循环次数，因为此时需要重复的字符串都在 sb中
                int cnt = multi_val.pop();
                StringBuilder tmp = new StringBuilder();
                for(int i = 0; i < cnt; i++) {
                    tmp.append(sb.toString());
                }
                // 此时当前层的解析已经完成，sb存放的是解析后的值，因为考虑到嵌套因素，要在前面把原来的字符串也加上
                sb = new StringBuilder().append(multi_char.pop()).append(tmp.toString());
                // 因为 [ 前的数字可能 > 10，所以需要统计以下数值
            } else if (x >= '0' && x <= '9') {
                v = v * 10 + Integer.valueOf(x + "");
            } else {
                // 普通情况就直接记录到 sb中
                sb.append(x);
            }
        }

        return sb.toString();
        
    }
}

[398] 随机数索引

给你一个可能含有 重复元素 的整数数组 nums ，请你随机输出给定的目标数字 target 的索引。你可以假设给定的数字一定存在于数组中。

实现 Solution 类：

Solution(int[] nums) 用数组 nums 初始化对象。
int pick(int target) 从 nums 中选出一个满足 nums[i] == target 的随机索引 i 。如果存在多个有效的索引，则每个索引的返回概率应当相等。

示例：

输入
["Solution", "pick", "pick", "pick"]
[[[1, 2, 3, 3, 3]], [3], [1], [3]]
输出
[null, 4, 0, 2]

解释
Solution solution = new Solution([1, 2, 3, 3, 3]);
solution.pick(3); // 随机返回索引 2, 3 或者 4 之一。每个索引的返回概率应该相等。
solution.pick(1); // 返回 0 。因为只有 nums[0] 等于 1 。
solution.pick(3); // 随机返回索引 2, 3 或者 4 之一。每个索引的返回概率应该相等。

提示：

1 <= nums.length <= 2 * 104
-231 <= nums[i] <= 231 - 1
target 是 nums 中的一个整数
最多调用 pick 函数 104 次

Related Topics

水塘抽样

哈希表

数学

随机化

解法一：

水塘抽样

class Solution {

    int[] nums;
    Random random;

    public Solution(int[] nums) {
        // 进来的 nums是乱序的
        this.nums = nums;
        random = new Random();
    }
    
    public int pick(int target) {
        int idx = 0, res = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == target) {
                // 核心步骤
                if (random.nextInt(++idx) == 0) {
                    res = i;
                }
            }
        }


        return res;
    }
}

[400] 第 N位数字

给你一个整数 n ，请你在无限的整数序列 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...] 中找出并返回第 n 位数字。

示例 1：
输入：n = 3
输出：3
示例 2：
输入：n = 11
输出：0
解释：第 11 位数字在序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... 里是 0 ，它是 10 的一部分。
提示：

1 <= n <= 231 - 1

Related Topics

数学

二分查找

解法一：

数学计算

这题不大明白

n < 10，直接返回
计算前缀部分，length表示全部被占用部分一共有多少位
计算尾部，推理出 num 和index

class Solution {
    public int findNthDigit(int n) {
        if (n < 10) {
            return n;
        }

        /*
        length表示整数序列的长度，比如说 三位数 -> length=9+180+2700
        cnt表示当前位数对应的数字个数，两位数 -> cnt=90
        i表示当前位数，比如说 10 -> i=2，两位长的数

        当退出循环时，i表示第n位数在一个 i位数（个位数、十位数。。）上
         */
        long length = 0, cnt = 9, i = 1;
        for (; length + cnt * i < n; i++) {
            length += cnt * i;
            cnt *= 10;
        }

        // 具体定位 i在哪一个数上
        long num = (long) Math.pow(10, i - 1) + (n - length - 1) / i;
        // 定位 n在 num中的第几位
        long index = (n - length - 1) % i;
        // 通过字符串的方法定位数字
        return String.valueOf(num).charAt((int) index) - '0';
    }
}

[416] 分割等和子集

给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：
输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2：
输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。
提示：

1 <= nums.length <= 200

1 <= nums[i] <= 100

Related Topics

数组

动态规划

解法一：

本质是一个 01背包问题，采用双层 dp数组

dp[i][j]表示 num[0 .. i]中的元素组成和为 j的可能性

class Solution {
    public boolean canPartition(int[] nums) {
        int sum = Arrays.stream(nums).sum();
        if (sum % 2 == 1) {
            return false;
        }

        int sumA = sum / 2;
        int len = nums.length;

        boolean[][] dp = new boolean[len + 1][sumA + 1];
		// 和为 0的时候，一定是 true
        for (int i = 0; i <= len; i++) {
            dp[i][0] = true;
        }

        for (int i = 1; i <= len; i++) {
            for (int j = 1; j <= sumA; j++) {
                // 双层 dp的推导式，没太理解
                if (j - nums[i - 1] >= 0) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }


        return dp[len][sumA];

    }

使用单层 dp数组，硬记就行

dp[0] = 1，内存循环从后往前（01背包）

class Solution {
    public boolean canPartition(int[] nums) {
        int sum = Arrays.stream(nums).sum();
        if (sum % 2 == 1) {
            return false;
        }

        int sumA = sum / 2;

        int[] dp = new int[sumA + 1];
        dp[0] = 1;

        for (int num : nums) {
            for (int i = sumA; i >= num; i--) {
                dp[i] += dp[i - num];
            }
        }

        return dp[sumA] != 0;
    }
}

[423] 从英文中重建数字

给你一个字符串 s ，其中包含字母顺序打乱的用英文单词表示的若干数字（0-9）。按升序返回原始的数字。

示例 1：
输入：s = "owoztneoer"
输出："012"
示例 2：
输入：s = "fviefuro"
输出："45"
提示：

1 <= s.length <= 105

s[i] 为 ["e","g","f","i","h","o","n","s","r","u","t","w","v","x","z"] 这些字符之一

s 保证是一个符合题目要求的字符串

Related Topics

哈希表

数学

字符串

解法一：

怪题要用怪方法

对比不同的英文单词，我们可以想到某几个英文字符是某几个数字所独有的。

比如说：

// z -> 0 zere
// x -> 6 six
// g -> 8 eight
// w -> 2 two
// u -> 4 four

那么针对那些没有独有字符的数字单词，我们可以通过字符相减的方法判断其存在的次数

比如说：

// 5 -> 'f '- 4，因为 4有独有字符 'u'，所以可以先找出来，然后再通过 'f'字符 - 4出现的次数，就是 5出现的次数了

class Solution {
    public String originalDigits(String s) {

        HashMap<Character, Integer> count = new HashMap<>();
        for (char c : s.toCharArray()) {
            count.put(c, count.getOrDefault(c, 0) + 1);
        }

        int[] arr = new int[10];
        arr[0] = count.getOrDefault('z', 0);
        arr[6] = count.getOrDefault('x', 0);
        arr[8] = count.getOrDefault('g', 0);
        arr[2] = count.getOrDefault('w', 0);
        arr[4] = count.getOrDefault('u', 0);

        arr[3] = count.getOrDefault('h', 0) - arr[8];
        arr[7] = count.getOrDefault('s', 0) - arr[6];
        arr[5] = count.getOrDefault('f', 0) - arr[4];
        arr[1] = count.getOrDefault('o', 0) - arr[4] - arr[2] - arr[0];
        arr[9] = count.getOrDefault('i', 0) - arr[5] - arr[6] - arr[8];
        // z -> 0 zere
        // x -> 6 six
        // g -> 8 eight
        // w -> 2 two
        // u -> 4 four

        // h -> 3 three
        // s -> 7 seven
        // v -> 5 five
        // o -> 1 one
        // i -> 9 nine

        StringBuffer sb = new StringBuffer();
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i]; j++) {
                sb.append((char) (i + '0'));
            }
        }

        return sb.toString();
    }
}

解法二：

高大上一些

通过数组遍历，实现数字的统计。

每次遍历一个数字单词，获取单词中的字母出现最少的频率，比如说 zero就会把 4个字母遍历一遍，找出现最少的次数，这个次数一定是该数字出现的最少次数。

然后，把在总的出现次数数组中，把当前这个字符串中的字符的次数删掉，方便下一个单词的统计。

class Solution {
    public String originalDigits(String s) {

        String[] ss = new String[]{"zero", "one", "two", "three", "four", "five", "six", "seven", "eight", "nine"};
        int[] priority = new int[]{0, 8, 6, 3, 2, 7, 5, 9, 4, 1};

        int n = s.length();
        int[] cnts = new int[26];

        // 统计字符串中，各个字符的出现次数
        for (int i = 0; i < n; i++) {
            cnts[s.charAt(i) - 'a']++;
        }

        StringBuilder sb = new StringBuilder();

        for (int i : priority) {
            int k = Integer.MAX_VALUE;
            // 确定单词出现的次数
            for (char c : ss[i].toCharArray()) {
                k = Math.min(k, cnts[c - 'a']);
            }

            // 减去当前单词出现的次数，方便下一个单词的统计
            for (char c : ss[i].toCharArray()) {
                cnts[c - 'a'] -= k;
            }

            // 依据次数添加到新字符串中
            while (k-- > 0) {
                sb.append(i);
            }
        }
        char[] cs = sb.toString().toCharArray();
        Arrays.sort(cs);
        return String.valueOf(cs);
    }
}

[435] 无重叠区间

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。
提示:

1 <= intervals.length <= 105

intervals[i].length == 2

-5 * 104 <= starti < endi <= 5 * 104

Related Topics

贪心

数组

动态规划

排序

解法一：

贪心

将所有数组按照左端点/右端点(无所谓)进行排序，然后判断当前的右端点是否小于下一个元素的左端点，如果是那么没有重叠，否则就算重叠了

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        if (intervals == null || intervals.length == 0) {
            return 0;
        }

        // 按照右边界排序
        Arrays.sort(intervals, (o1, o2) -> o1[1]-o2[1]);
        int res = 0;
        int x_end = intervals[0][1];

        for(int i = 1; i < intervals.length; i++) {
            int[] cur = intervals[i];
            // 判断是否存在重叠
            if (cur[0] < x_end) {
                res++;
                continue;
            } 

            x_end = cur[1];
        }

        return res;
    }
}

[438] 找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

示例 1:

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

示例 2:

输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

提示:

1 <= s.length, p.length <= 3 * 104
s 和 p 仅包含小写字母

Related Topics

哈希表

字符串

滑动窗口

解法一：

滑动窗口

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> res = new ArrayList<>();
        HashMap<Character, Integer> need = new HashMap<>(p.length());
        HashMap<Character, Integer> window = new HashMap<>();

        // 记录需要的字符串
        for (int i = 0; i < p.length(); i++) {
            char in = p.charAt(i);
            need.put(in, need.getOrDefault(in, 0) + 1);
        }

        int left = 0, right = 0;
        int valid = 0;

        while (right < s.length()) {
            char rChar = s.charAt(right);
            right++;
            window.put(rChar, window.getOrDefault(rChar, 0) + 1);
            if (need.containsKey(rChar)) {
                if (need.get(rChar).equals(window.get(rChar))) {
                    valid++;
                }
            }

            while (valid == need.size()) {
                if (right - left == p.length()) {
                    res.add(left);
                }
                char lChar = s.charAt(left);
                left++;
                if (need.containsKey(lChar)) {
                    if (need.get(lChar).equals(window.get(lChar))) {
                        valid--;
                    }
                    window.put(lChar, window.get(lChar) - 1);
                }
            }
        }
        return res;
    }
}

[450] 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:

节点数的范围 [0, 104].

-105 <= Node.val <= 105

节点值唯一

root 是合法的二叉搜索树

-105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

Related Topics

树

二叉搜索树

二叉树

解法一：

普通的 BST的递归遍历，找到待删除的元素之后

如果它的左右子树有一个为空，就将其的右左子树替代它

如果都不为空，就使用其右子树中的最小节点代替它

但是这里直接用 val的赋值来实现节点的替代

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        // base condition
        if (root == null) {
            return root;
        }
        // 找到了
        if (root.val == key) {
            // 该节点的左右子树至少缺一个
            if (root.left == null) {
                return root.right;
            }
            if (root.right == null) {
                return root.left;
            }
			// 左右子树都健全，就需要找到右子树中的最小节点，来代替被删除的节点
            TreeNode rightMinNode = getMinNode(root.right);
            // 这里是直接把值给拷贝了过来
            root.val = rightMinNode.val;
            // 记得把之前右子树中的最小的节点删掉
            root.right = deleteNode(root.right, root.val);
            // 没找到
        } else if (root.val > key) {
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
        }

        return root;
    }

    // 定位直接的后继结点
    private TreeNode getMinNode(TreeNode node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }
}

如果不用值的替代，而是货真价实的节点替换，就用如下代码：

注意：因为递归的关系，不需要手动记录前置节点，只需要把递归的结果值赋值回去就行了

TreeNode rightMinNode = getMinNode(root.right);
// 把 root更新了
root.right = deleteNode(root.right, rightMinNode.val);
// 把 root的左右子树赋值给新的那个节点
rightMinNode.left = root.left;
rightMinNode.right = root.right;
// 再把 root的引用也赋值过去
root = rightMinNode;

第二次手写

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return root;
        if (root.val == key) {
            if (root.left == null) {
                return root.right;
            } else if (root.right == null) {
                return root.left;
            }

            TreeNode t1 = root.right, t2 = t1.left;
            if (t2==null) {
                t1.left = root.left;
                return t1;
            } else {
                while (t2.left != null) {
                    t2 = t2.left;
                    t1 = t1.left;
                }

                t1.left = t2.right;
                t2.left = root.left;
                t2.right = root.right;
                return t2;
            }
            

        } else if (root.val > key) {
            root.left = deleteNode(root.left, key);
        } else {
            root.right = deleteNode(root.right, key);
        }

        return root;
        
    }
}

[452] 用最少数量的箭引爆气球

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 x``start，x``end，且满足 xstart ≤ x ≤ x``end，则该气球会被引爆。可以射出的弓箭的数量 没有限制 。弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的最小弓箭数 。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:
- 在x = 2处发射箭，击破气球[1,2]和[2,3]。
- 在x = 4处射出箭，击破气球[3,4]和[4,5]。

提示:

1 <= points.length <= 105
points[i].length == 2
-231 <= xstart < xend <= 231 - 1

Related Topics

贪心

数组

排序

解法一：

贪心，基本同435

class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points == null || points.length == 0) {
            return 0;
        }

        // 测试用例中有一个 -21亿 和 +21亿的值，因此无法二者相减
        Arrays.sort(points, (o1, o2)->Integer.compare(o1[1], o2[1]));

        int cnt = 1;
        int end = points[0][1]; 
        for(int i = 0; i < points.length; i++) {
            if (points[i][0] > end) {
                cnt++;
                end = points[i][1];
            }
        }
        return cnt;
    }
}

[494] 目标和

给你一个整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：
输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2：
输入：nums = [1], target = 1
输出：1
提示：

1 <= nums.length <= 20

0 <= nums[i] <= 1000

0 <= sum(nums[i]) <= 1000

-1000 <= target <= 1000

Related Topics

数组

动态规划

回溯

解法一：

回溯

先加后减，然后先减后加；

存在大量冗余计算，低效

class Solution {
    int res = 0;

    public int findTargetSumWays(int[] nums, int target) {
        if (nums.length == 0) {
            return 0;
        }

        traverse(nums, target, 0);
        return res;
    }

    private void traverse(int[] nums, int target, int idx) {
        if (idx == nums.length) {
            // 采用的是对 target求减操作，因此当 target == 0时，可看作那几个数组元素恰好组成和为 target
            if (target == 0) {
                res++;
            }
            return;
        }

       /*
       可以理解为
       
       target -= nums[idx];
       traverse(nums, target, idx + 1);
       target += nums[idx];
     
	   target += nums[idx];
       traverse(nums, target, idx + 1);
       target -= nums[idx];
       */
        traverse(nums, target - nums[idx], idx + 1);
        traverse(nums, target + nums[idx], idx + 1);
    }
}

❤ 解法二：

动态规划

看作集合划分背包问题

可以把 nums[]划分成两个子集 A 和 B，分别代表正数和负数，他们与 target存在如下关系

sum(A) - sum(B) == target，即 sum(A) = sum(B) + target，即 sum(A) + sum(A) = target + sum(B) + sum(A)，即 sum(A) = (target + sum(nums)) / 2

因此原问题转变为在 nums[]数组中找出集合 A，使其和为 (target + sum(nums)) / 2

在这里，num[]数组中单个元素只能用一次，所以可以也可以看作是 0, 1背包问题，需要遍历背包时，要从后向前遍历；

并且，这道题问的是分组，所以先遍历物品，再遍历背包；

并且因为是求数量，所以 dp[0] = 1

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        // A - B = target;
        // A = target + B
        // 2A = target + sum
        // A = (target + sum) / 2;

        int sumA = Arrays.stream(nums).sum() + target;
        if (sumA % 2 == 1 || sumA < 0) {
            return 0;
        }

        // sumA即要找的集合的总和值
        sumA /= 2;
        int[] dp = new int[sumA + 1];
        dp[0] = 1;

        // 注意 双层 for的顺序，和内部的遍历方向
        for (int num : nums) {
            for (int i = sumA; i >= num; i--) {
                dp[i] += dp[i - num];
            }
        }

        return dp[sumA];
    }
}

[503] 下一个更大元素Ⅱ

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。
注意: 输入数组的长度不会超过 10000。

Related Topics

栈

数组

单调栈

解法一：

单调栈

使用倍长数组来体现数组循环

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int[] res = new int[nums.length];
        Stack<Integer> stack = new Stack<>();

        // 使用两倍的数组长度来计算，借此来实现循环的功能
        for (int i = 2 * nums.length - 1; i >= 0; i--) {
            while (!stack.isEmpty() && stack.peek() <= nums[i % nums.length]) {
                stack.pop();
            }

            res[i % nums.length] = stack.isEmpty() ? -1 : stack.peek();
            stack.push(nums[i % nums.length]);
        }

        return res;
    }
}

[516] 最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：
输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。
示例 2：
输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。
提示：

1 <= s.length <= 1000

s 仅由小写英文字母组成

Related Topics

字符串

动态规划

解法一：

将 dp[i, j]看坐字符串从 i 到 j中的回文子序列的长度

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len][len];
        for (int i = 0; i < len; i++) {
            dp[i][i] = 1;
        }

        for (int i = len - 1; i >= 0; i--) {
            for (int j = i + 1; j < len; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[0][len - 1];
    }
}

想不通的时候，就把它看作字符串 s和它的反转后的字符串 rs之间的最长相同序列

class Solution {
    public int longestPalindromeSubseq(String s) {
        // 反转
        String s1 = new StringBuffer(s).reverse().toString();
        // 求两个字符串的最长相同子序列
        return findLongestCommonSubsequence(s, s1);
    }

    private int findLongestCommonSubsequence(String s1, String s2) {
        int[][] dp = new int[s1.length() + 1][s2.length() + 1];
        // base case 就是 0

        for(int i = 1; i <= s1.length(); i++) {
            for(int j = 1; j <= s2.length(); j++) {
                if (s1.charAt(i-1) == s2.charAt(j-1)) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i-1][j], Math.max(dp[i-1][j-1], dp[i][j-1]));
                }
            }
        }

        return dp[s1.length()][s2.length()];
    }
}

[518] ❤ 零钱兑换Ⅱ

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：
输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2：
输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。
示例 3：
输入：amount = 10, coins = [10] 
输出：1
提示：

1 <= coins.length <= 300

1 <= coins[i] <= 5000

coins 中的所有值 互不相同

0 <= amount <= 5000

Related Topics

数组

动态规划

解法一：

背包问题

首先，我对背包问题并不清楚。

初见时，用动态规划写成了针对排序的 dp，也就是说会把 1+2 和 2+1，区分开来；

而题目要求是组合，也就是说 1+2 和 2+1应当看作一样的。

具体的方法是，限制 coin的加入顺序，也就是说，强制 coin是从小到大排列，避免出现 2+1的情况

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        dp[0] = 1;

        // 注意，外层为 coin，内层为 amount
        for (int coin : coins) {
            for (int i = coin; i <= amount; i++) {
                dp[i] += dp[i - coin];
            }
        }
        return dp[amount];
    }
}

同理，思考爬楼梯题目，为什么那道题很轻松，因为明确了每次只能爬 1 ~ 2级台阶，所以可得

for(int i = 1; i <= 台阶总数; i++) {
	dp[i] = dp[i-1] + dp[i-2];
}

但是，如果每次可以爬的台阶也是不确定的，也是传入的一个数组中的可能的值，那么就更本体一样了；

爬台阶同样要求的也是得到组合，也需要在外层 for循环中，先遍历可以爬的级数，再遍历 dp

背包问题总结

如果是问填满背包，则递推式为 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

如果是问填满背包有多少个方法，则为dp[j] += dp[j-coins[i]]

如果是01背包问题，则物品只能用一次，j必须从后向前遍历 for (int j = amount; j >= coins[i]; j--)

如果是完全背包问题，则物品能用无数次，j必须从前向后遍历 for (j = coins[i]; j <= amount; j++)

先循环物品还是先循环背包容量？如果懒得判断的话就直接先物品再背包容量，99%对。

01背包中二维dp数组的两个for遍历的先后循序是可以颠倒的，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量（否则前面的值会被覆盖）

在纯完全背包中，对于一维 dp数组来说，其实两个 for循环嵌套顺序同样无所谓！因为dp[j] 是根据下标 j之前所对应的dp[j]计算出来的。只要保证下标 j之前的 dp[j]都是经过计算的就可以了。有些问多少种方法填满的变种题，i,j的顺序涉及到组合排列--物品,容量为组合。容量,物品为排列

dp[0]初始化。问填满背包的方法，dp[0]=1;问能否填满背包，dp[0]=true

动态规划五部曲

定义dp

递推公式

初始化

确定遍历i,j 顺序和 j方向

举例推导验证

遍历顺序:完全背包的两个for循环的先后顺序都是可以的。

分类解题模板
背包问题大体的解题模板是两层循环，分别遍历物品nums和背包容量target，然后写转移方程，
根据背包的分类我们确定物品和容量遍历的先后顺序，根据问题的分类我们确定状态转移方程的写法

首先是背包分类的模板：
1、0/1背包：外循环nums,内循环target,target倒序且 target>=nums[i];
2、完全背包：外循环nums,内循环target,target正序且 target>=nums[i];
3、组合背包：外循环target,内循环nums,target正序且 target>=nums[i];
4、分组背包：这个比较特殊，需要三重循环：外循环背包bags,内部两层循环根据题目的要求转化为1,2,3三种背包类型的模板

然后是问题分类的模板：
1、最值问题: dp[i] = max/min(dp[i], dp[i-nums]+1)或dp[i] = max/min(dp[i], dp[i-num]+nums);
2、存在问题(bool)：dp[i]=dp[i]||dp[i-num];
3、组合问题：dp[i]+=dp[i-num];

[523] 连续的子数组和

给你一个整数数组 nums 和一个整数 k ，编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组：

子数组大小 至少为 2 ，且
子数组元素总和为 k 的倍数。

如果存在，返回 true ；否则，返回 false 。

如果存在一个整数 n ，令整数 x 符合 x = n * k ，则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。

示例 1：
输入：nums = [23,2,4,6,7], k = 6
输出：true
解释：[2,4] 是一个大小为 2 的子数组，并且和为 6 。
示例 2：
输入：nums = [23,2,6,4,7], k = 6
输出：true
解释：[23, 2, 6, 4, 7] 是大小为 5 的子数组，并且和为 42 。 
42 是 6 的倍数，因为 42 = 7 * 6 且 7 是一个整数。
示例 3：
输入：nums = [23,2,6,4,7], k = 13
输出：false
提示：

1 <= nums.length <= 105

0 <= nums[i] <= 109

0 <= sum(nums[i]) <= 231 - 1

1 <= k <= 231 - 1

Related Topics

数组

哈希表

数学

前缀和

解法一：

前缀和+同余定理

同余定理就是说：如果 (a - b) %k == 0 那么 a%k == b%k

这道题，单纯的前缀和会超时，第94个用例有 10的四次方个，因此必须用空间换时间；

class Solution {
    public boolean checkSubarraySum(int[] nums, int k) {
        int[] pre = new int[nums.length + 1];
        pre[0] = 0;
        
        for(int i = 0; i < nums.length; i++) {
            pre[i + 1] = pre[i] + nums[i];
        }

        HashSet<Integer> set = new HashSet<>();
        for(int i = 2; i <= nums.length; i++) {
            // 这步我不理解，为什么这样就能实现子数组长度大于 2？
            set.add(pre[i-2] % k);
            if (set.contains(pre[i] % k)) {
                return true;
            }
        }

        return false;
    }
}

[528] 按权重随机选择

给你一个 下标从 0 开始 的正整数数组 w ，其中 w[i] 代表第 i 个下标的权重。

请你实现一个函数 pickIndex ，它可以 随机地 从范围 [0, w.length - 1] 内（含 0 和 w.length - 1）选出并返回一个下标。选取下标 i 的概率为 w[i] / sum(w) 。

例如，对于 w = [1, 3]，挑选下标 0 的概率为 1 / (1 + 3) = 0.25 （即，25%），而选取下标 1 的概率为 3 / (1 + 3) = 0.75（即，75%）。

示例 1：

输入：
["Solution","pickIndex"]
[[[1]],[]]
输出：
[null,0]
解释：
Solution solution = new Solution([1]);
solution.pickIndex(); // 返回 0，因为数组中只有一个元素，所以唯一的选择是返回下标 0。

示例 2：

输入：
["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
[[[1,3]],[],[],[],[],[]]
输出：
[null,1,1,1,1,0]
解释：
Solution solution = new Solution([1, 3]);
solution.pickIndex(); // 返回 1，返回下标 1，返回该下标概率为 3/4 。
solution.pickIndex(); // 返回 1
solution.pickIndex(); // 返回 1
solution.pickIndex(); // 返回 1
solution.pickIndex(); // 返回 0，返回下标 0，返回该下标概率为 1/4 。

由于这是一个随机问题，允许多个答案，因此下列输出都可以被认为是正确的:
[null,1,1,1,1,0]
[null,1,1,1,1,1]
[null,1,1,1,0,0]
[null,1,1,1,0,1]
[null,1,0,1,0,0]
......
诸若此类。

提示：

1 <= w.length <= 104
1 <= w[i] <= 105
pickIndex 将被调用不超过 104 次

Related Topics

数学

二分查找

前缀和

随机化

解法一：

前缀和+二分查找

class Solution {

    int[] preSum;
    Random random;
    int len;

    public Solution(int[] w) {
        len = w.length;
        preSum = new int[len];
        // 构造前缀和数组
        preSum[0] = w[0];
        for(int i = 1; i <len; i++) {
            preSum[i] = preSum[i-1] + w[i];
        }
        random = new Random();
    }
    
    public int pickIndex() {
        // 随机生成一个值，然后找它在前缀和数组中的右边界
        // 右边界的下标就是待返回的值
        int target = random.nextInt(preSum[len - 1]);
        int left = 0, right = len;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (preSum[mid] == target) {
                left = mid + 1;
            } else if (preSum[mid] > target) {
                right = mid;
            } else if (preSum[mid] < target) {
                left = mid + 1;
            }
        }

        return left;
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(w);
 * int param_1 = obj.pickIndex();
 */

[538] 把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2：
输入：root = [0,null,1]
输出：[1,null,1]
示例 3：
输入：root = [1,0,2]
输出：[3,3,2]
示例 4：
输入：root = [3,2,4,1]
输出：[7,9,4,10]
提示：

树中的节点数介于 0 和 104 之间。

每个节点的值介于 -104 和 104 之间。

树中的所有值 互不相同 。

给定的树为二叉搜索树。

Related Topics

树

深度优先搜索

二叉搜索树

二叉树

解法一：

倒着遍历

遍历顺序为右中左，先找最右边，然后中间，然后左边；然后再右边的上一个节点

期间记录上一个节点的值

class Solution {
    // 记录上一个节点的值
    int prev = 0;

    public TreeNode convertBST(TreeNode root) {
        build(root);
        return root;
    }

    private void build(TreeNode root) {
        if (root == null) {
            return;
        }
		// 右中左
        build(root.right);
        // 更新当前节点的值
        root.val += prev;
        prev = root.val;
        build(root.left);
    }
}

[560] 和为 K的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的连续子数组的个数

示例 1：
输入：nums = [1,1,1], k = 2
输出：2
示例 2：
输入：nums = [1,2,3], k = 3
输出：2
提示：

1 <= nums.length <= 2 * 104

-1000 <= nums[i] <= 1000

-107 <= k <= 107

Related Topics

数组

哈希表

前缀和

解法一：

暴力枚举，创建一个和 sum，遍历数组，sum+=元素的值并判断是否等于 k；每一大轮后都置空 sum

class Solution {
    public int subarraySum(int[] nums, int k) {
        if (nums == null || nums.length == 0) {
            return 0;
        }

        int sum = 0;
        int res = 0;

        for (int i = 0; i < nums.length; i++) {
            for (int j = i; j < nums.length; j++) {
                // sum每次加
                sum += nums[j];
                // 判断
                if (sum == k) {
                    res++;
                }
            }
            // 下一轮开始前，置空
            sum = 0;
        }
        // 返回结果
        return res;
    }
}

解法二：简单前缀和

创建一个额外的数组，记录前缀和，但是实际判断是不是符合 k时，依旧需要嵌套循环

class Solution {
    public int subarraySum(int[] nums, int k) {

        int[] preSum = new int[nums.length + 1];
        
        // 构建前缀和数组
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }

        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = i; j < nums.length; j++) {
                if ((preSum[j + 1] - preSum[i]) == k) {
                    res++;
                }
            }
        }

        return res;
    }
}

❤ 解法三：前缀和优化

使用 HashMap来记录，键是前缀和，值是次数

因为使用前缀和时的公式是这样的：preSum[i] - preSum[j] == k，所以可以判断 preSum[j]的存在个数即可，preSum[j] = preSum[i] - k，亦即 map.get(preSum[i] - k)

class Solution {
    public int subarraySum(int[] nums, int k) {
        
        int res = 0, preSum = 0;
        HashMap<Integer, Integer> map = new HashMap<>();
        // 注意添加这一项，因为一开始没有元素的时候，preSum是视作 0的
        map.put(0, 1);
        
        for (int i = 0; i < nums.length; i++) {
            // 构造前缀和
            preSum += nums[i];
            // 判断 preSum-k这个键是否存在
            if (map.containsKey(preSum - k)) {
                res += map.get(preSum - k);
            }
            // 不管如何，preSum还是依旧一定要更新的
            map.put(preSum, map.getOrDefault(preSum, 0) + 1);
        }
        return res;
    }
}

[567] 字符串的排列

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的子串。

示例 1：
输入：s1 = "ab" s2 = "eidbaooo"
输出：true
解释：s2 包含 s1 的排列之一 ("ba").
示例 2：
输入：s1= "ab" s2 = "eidboaoo"
输出：false
提示：

1 <= s1.length, s2.length <= 104

s1 和 s2 仅包含小写字母

Related Topics

哈希表

双指针

字符串

滑动窗口

解法一：

滑动窗口

class Solution {
    public boolean checkInclusion(String s1, String s2) {

        // 声明两个哈希表，分别存储需要的字符信息，和窗口中的字符信息，注意 windows中的字符只存 need中需要的字符
        HashMap<Character, Integer> need = new HashMap<>();
        HashMap<Character, Integer> window = new HashMap<>();

        int s1Len = s1.length();
        int s2Len = s2.length();

        // 初始化 need，对于某一个重复的字符，它的 value会大于 1
        for (int i = 0; i < s1Len; i++) {
            char key = s1.charAt(i);
            need.put(key, need.getOrDefault(key, 0) + 1);
        }

        // 左右边界
        int left = 0, right = 0;
        // 判断字符数量是否符合要求
        int valid = 0;

        // 开始滑动
        while (right < s2Len) {
            // 获取右边界字符
            char c = s2.charAt(right);
            right++;

            // 判断这个字符是不是需要的
            if (need.containsKey(c)) {
                // 如果需要就放到 window中，并把该字符对应的值加一
                window.put(c, window.getOrDefault(c, 0) + 1);
                // 如果这个字符的数量符合要求了 valid加一
                if (need.get(c).equals(window.get(c))) {
                    valid++;
                }
            }

            // 因为要求 window中的某一个子串序列中的字符是 need中的字符，所以可以设置条件为 right - left > s1Len
            // 即当窗口长度大于等于 s1的时候，就进行左侧窗口的收缩
            while (right - left  >= s1Len) {

                // 如果窗口中字符需要的状况等于 s1的状况，那么就认为是存在该子串
                if (valid == need.size()) {
                    return true;
                }

                // 否则，获取最左字符
                char leftChar = s2.charAt(left);
                // 左窗口右移
                left++;

                // 如果最左字符是需要的字符，那么就需要进行修改 valid和 window表
                if (need.containsKey(leftChar)) {
                    if (window.get(leftChar).equals(need.get(leftChar))) {
                        valid--;
                    }
                    window.put(leftChar, window.getOrDefault(leftChar, 0) - 1);
                }
            }

        }

        // 如果全部遍历完了，还没提前返回，就说明没有，返回 false
        return false;
    }
}

再次手写

class Solution {
    public boolean checkInclusion(String s1, String s2) {

        Map<Character, Integer> window = new HashMap<>(), need = new HashMap<>();

        // 先把 need集合构件好
        for(char x : s1.toCharArray()) {
            need.put(x, need.getOrDefault(x, 0) + 1);
        }
        
        int left = 0, right = 0;
        int valid = 0;
        
        while(right < s2.length()) {
            char in = s2.charAt(right);
            right++;

            // 滑动窗口中只添加 need中需要的字符
            if (need.containsKey(in)) {
                window.put(in, window.getOrDefault(in, 0) + 1);
                if (window.get(in).equals(need.get(in))) {
                    valid++;
                }
            }


            while (right - left >= s1.length()) {
                if(valid == need.size()) {
                    return true;
                }

                char out = s2.charAt(left);
                left++;
                
                if (need.containsKey(out)) {
                    if (need.get(out).equals(window.get(out))) {
                        valid--;
                    }
                    window.put(out, window.get(out) - 1);
                }
            }
        }

        return false;
    }
}

[581] 最短无序连续子数组

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的最短子数组，并输出它的长度。

示例 1：
输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。
示例 2：
输入：nums = [1,2,3,4]
输出：0
示例 3：
输入：nums = [1]
输出：0
提示：

1 <= nums.length <= 104

-105 <= nums[i] <= 105

进阶：你可以设计一个时间复杂度为 O(n) 的解决方案吗？

Related Topics

栈

贪心

数组

双指针

排序

单调栈

解法一：

其实就是找数组元素第一处乱序的地方和最后一处乱序的地方

将数组排序后对比原数组，第一个不一致的地方就是开始；

最后一个不一致的地方就是结束；

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        // 2,6,4,8,10,9,15
        // 2,4,6,8,9,10,15

        if (nums == null || nums.length < 2) {
            return 0;
        }

        int[] back = nums.clone();
        Arrays.sort(nums);

        int i = 0, j = nums.length - 1;
        while(i <= j && nums[i] == back[i]) {
            i++;
        }
        while(i <= j && nums[j] == back[j]) {
            j--;
        }

        return j - i  + 1;
        
    }
}

解法二：

不拷贝数组，直接遍历

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        // 2,6,4,8,10,9,15
        // 2,4,6,8,9,10,15
        if (nums == null || nums.length < 2) {
            return 0;
        }

        int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
        int left = 0, right = 0;

        // 找到最右侧的逆序处
        for(int i = 0; i < nums.length; i++) {
            // 之所以要用 max 而不是 nums[i-1]是因为可能 nums[i-1]也是逆序的
            if (nums[i] < max ) {
                right = i;
            }
            max = Math.max(max, nums[i]);
        }

        // 找到最左侧的逆序处
        for(int i = right; i >= 0; i--) {
            if (nums[i] > min) {
                left = i;
            }
            min = Math.min(min, nums[i]);
        }

        return left == right ? 0 : right - left + 1;
    }
}

[583] 两个字符串的删除操作

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步可以删除任意一个字符串中的一个字符。

示例 1：
输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"
示例 2:
输入：word1 = "leetcode", word2 = "etco"
输出：4
提示：

1 <= word1.length, word2.length <= 500

word1 和 word2 只包含小写英文字母

Related Topics

字符串

动态规划

解法一：

类比编辑距离，直接计算删除次数

举个例子，画个二维表，找关系

class Solution {
    public int minDistance(String word1, String word2) {
        int row = word1.length();
        int col = word2.length();
        // 记录最长公共子序列
        int[][] dp = new int[row + 1][col + 1];

        for (int i = 0; i <= row; i++) {
            dp[i][0] = i;
        }

        for (int i = 0; i <= col; i++) {
            dp[0][i] = i;
        }
		// 注意这个关系的寻找，别想的太多，这种题都差不多
        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                }
            }
        }

        return dp[row][col];
    }
}

解法二：

类比最长公共子序列，先求出最长公共子序列，这个就是删除后的结果值，那么两个字符串的长度减去它两次就是需要删除的数量了

class Solution {
    public int minDistance(String word1, String word2) {
        int row = word1.length();
        int col = word2.length();
        // 记录最长公共子序列
        int[][] dp = new int[row + 1][col + 1];

        for (int i = 0; i <= row; i++) {
            dp[i][0] = i;
        }

        for (int i = 0; i <= col; i++) {
            dp[0][i] = i;
        }

        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                }
            }
        }

        return dp[row][col];
    }
}

[621] 任务调度器

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

示例 1：

输入：tasks = ["A","A","A","B","B","B"], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
  在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。

示例 2：

输入：tasks = ["A","A","A","B","B","B"], n = 0
输出：6
解释：在这种情况下，任何大小为 6 的排列都可以满足要求，因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类

示例 3：

输入：tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出：16
解释：一种可能的解决方案是：
  A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A

提示：

1 <= task.length <= 104
tasks[i] 是大写英文字母
n 的取值范围为 [0, 100]

Related Topics

贪心

数组

哈希表

计数

排序

堆（优先队列）

解法一：

模拟+贪心？

先找到最长的序列，然后把架子搭出来，剩下的那些元素都查到间隙里面就行；

如果间隙不够插了，就硬插，把间隔扩大，且此时间隔肯定 > n了

class Solution {
    public int leastInterval(char[] tasks, int n) {
        int res = 0;
        int[] freq = new int[26];
        // 统计频率
        for(char x : tasks) {
            freq[x - 'A']++;
        }
        // 排序
        Arrays.sort(freq);

        // 搭架子，eg: A最多，则序列可以是 A _ _ A _ _ A _ _ A
        // 之后只需要在 _ 上放元素就行，并且因为架子已经好了，所以后续放的元素一定也是满足 n 间隙的
        res = (freq[25] - 1) * (n + 1) + 1;
        
        int idx = 24;
        while(idx >= 0) {
            // 如果存在一个跟 A 一样多的元素，那么就会变成 AB_AB_AB_AB，最后再额外加一个 B
            if (freq[idx] == freq[25]) {
                res++;
            }
            idx--;
        }
        // 如果被占满了，假设 ABCABCADD n=2，这种情况两个 D之间也需要冷却，此时可以把 D随便插到 A之间，因为插入后，所有元素的间距都会变大
        // 并且，占满也就意味着，没有空位，那么也就是 task的长度
        return Math.max(res, tasks.length);
    }
}

[622] 设计循环队列

设计你的循环队列实现。循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

示例：

MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1);  // 返回 true
circularQueue.enQueue(2);  // 返回 true
circularQueue.enQueue(3);  // 返回 true
circularQueue.enQueue(4);  // 返回 false，队列已满
circularQueue.Rear();  // 返回 3
circularQueue.isFull();  // 返回 true
circularQueue.deQueue();  // 返回 true
circularQueue.enQueue(4);  // 返回 true
circularQueue.Rear();  // 返回 4

提示：

所有的值都在 0 至 1000 的范围内；
操作数将在 1 至 1000 的范围内；
请不要使用内置的队列库。

Related Topics

设计

队列

数组

链表

解法一：

数组实现

class MyCircularQueue {

    int[] arr;
    int putIdx;
    int takeIdx;
    int len;
    // 理论上，isFull 和 isEmpty都应该是能通过 putIdx 和 takeIdx直接获取的
    // 见严蔚敏版数据结构的队列那一章，但我失败了
    int size;

    public MyCircularQueue(int k) {
        arr = new int[k];
        putIdx = 0;
        takeIdx = 0;
        len = k;
        size = 0;
    }
    
    public boolean enQueue(int value) {
        if (isFull()) {
            return false;
        }

        arr[putIdx] = value;
        putIdx = (putIdx + 1) % len;
        size++;
        return true;
    }
    
    public boolean deQueue() {
        if (isEmpty()) {
            return false;
        }
        arr[takeIdx] = -1;
        takeIdx = (takeIdx + 1) % len;
        size--;
        return true;
    }
    
    public int Front() {
        if (isEmpty()) {
            return -1;
        }
        return arr[takeIdx];
    }
    
    public int Rear() {
        if (isEmpty()) {
            return -1;
        }
        return arr[(putIdx - 1 + len) % len];
    }
    
    public boolean isEmpty() {
        return size == 0;
    }
    
    public boolean isFull() {
        return size == len;
    }
}

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue obj = new MyCircularQueue(k);
 * boolean param_1 = obj.enQueue(value);
 * boolean param_2 = obj.deQueue();
 * int param_3 = obj.Front();
 * int param_4 = obj.Rear();
 * boolean param_5 = obj.isEmpty();
 * boolean param_6 = obj.isFull();
 */

[652] 寻找重复的子树

给定一棵二叉树 root，返回所有重复的子树。

对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

如果两棵树具有相同的结构和相同的结点值，则它们是重复的。

示例 1：
输入：root = [1,2,3,4,null,2,4,null,null,4]
输出：[[2,4],[4]]
示例 2：
输入：root = [2,1,1]
输出：[[1]]
示例 3：
输入：root = [2,2,2,3,null,3,null]
输出：[[2,3],[3]]
提示：

树中的结点数在[1,10^4]范围内。

-200 <= Node.val <= 200

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

解法一：

我们没办法只靠递归边记录边判断，因为我不知道其他子树的状态？

因此，可以额外设置一个全局的记录每次遍历时子树的状态。
我们怎么记录状态？

比较憨憨的用字符串进行拼接得到状态值，并且因为可能存在值相同但是结构不同的情况，所以要把 null也表示进去，也就是指明了叶子节点

class Solution {
    List<TreeNode> res = new ArrayList<>();
    HashMap<String, Integer> map = new HashMap<>();

    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        traverse(root);
        return res;
    }

    private String traverse(TreeNode root) {
        // base condition
        if (root == null) {
            return "#";
        }

        // 获取左右子树的状态值
        String left = traverse(root.left);
        String right = traverse(root.right);
        // 构造当前子树的状态值
        String cur = left + "," + right + "," + root.val;

        // 借助哈希表
        map.put(cur, map.getOrDefault(cur, 0) + 1);
        if (map.get(cur) == 2) {
            res.add(root);
        }

        return cur;
    }
}

第二次手写

class Solution {
    // 难点在于将当前的子树情况和其它的进行比较！为此，必须引入容器暂存每次遍历的结果
    List<TreeNode> res = new ArrayList<>();
    Map<String, Integer> map = new HashMap<>();
    
    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        traverse(root);
        return res;
    }

    private String traverse(TreeNode root) {
        if (root == null) {
            return "#";
        }

        String left = traverse(root.left);
        String right = traverse(root.right);
        String cur = left + "," + right + "," + root.val;
        map.put(cur, map.getOrDefault(cur, 0) + 1);
        if (map.get(cur) == 2) {
            res.add(root);
        }
        return cur;
    }
}

[654] 最大二叉树

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。

返回有给定数组 nums 构建的 最大二叉树 。

示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

Related Topics

栈

树

数组

分治

二叉树

单调栈

解法一：

遍历+递归

遍历数组的区间范围，找到最大值为当前子树的根；

递归左右范围作为左右子树的根节点

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length);
    }

    private TreeNode build(int[] nums, int left, int right) {
        if (left >= right) {
            return null;
        }

        // 找到最大值
        int max = nums[left];
        int maxCnt = left;
        for (int i = left; i < right; i++) {
            if (nums[i] > max) {
                maxCnt = i;
                max = nums[i];
            }
        }

        // 构造根节点
        TreeNode root = new TreeNode(max);
        // 递归构造左右子树
        root.left = build(nums, left, maxCnt);
        root.right = build(nums, maxCnt + 1, right);
        return root;
    }
}

第二次手写

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        if (nums == null || nums.length == 0) {
            return null;
        }

        return traverse(nums, 0, nums.length-1);
    }

    private TreeNode traverse(int[] nums, int left, int right) {
        if (left > right) {
            return null;
        }

        int max = nums[left], idx = left;
        for(int i = left; i <= right; i++) {
            if (nums[i] > max) {
                max = nums[i];
                idx = i;
            }
        }

        TreeNode root = new TreeNode(max);
        root.left = traverse(nums, left, idx - 1);
        root.right = traverse(nums, idx + 1, right);

        return root;
    }

}

[674] 回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：
输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"
示例 2：
输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示：

1 <= s.length <= 1000

s 由小写英文字母组成

Related Topics

字符串

动态规划

解法一：

中心扩散

class Solution {
    int res = 0;
    
    public int countSubstrings(String s) {
        for(int i = 0; i < s.length(); i++) {
            traverse(s, i, i);
            traverse(s, i, i+1);
        }
        return res;
    }

    private void traverse(String s, int left, int right) {
        while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            res++;
            left--;
            right++;
        }
    }
}

[698] 划分为 k个相等的子集

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

示例 1：
输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。
提示：

1 <= k <= len(nums) <= 16

0 < nums[i] < 10000

Related Topics

位运算

记忆化搜索

数组

动态规划

回溯

状态压缩

解法一：

以 nums[]数组中元素的视角，进行回溯递归

class Solution {
    public boolean canPartitionKSubsets(int[] nums, int k) {
        // 先排除一些乱七八糟的情况
        if (k > nums.length) {
            return false;
        }

        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (sum % k != 0) {
            return false;
        }

        int[] bucket = new int[k];
        int target = sum / k;
        return backtrace(nums, 0, bucket, target);
    }

    /**
     * 回溯遍历每一种可能，即会对每一个 nums中的元素进行 K次递归
     *
     * @param nums
     * @param index  表示当前是 nums中的第几个元素
     * @param bucket
     * @param target
     * @return
     */
    public boolean backtrace(int[] nums, int index, int[] bucket, int target) {
        // 如果所有元素都遍历完了
        if (index == nums.length) {
            // 检查每一个桶
            for (int i = 0; i < bucket.length; i++) {
                if (bucket[i] != target) {
                    return false;
                }
            }

            return true;
        }

        // 穷举 nums[i]可能装入的桶
        for (int i = 0; i < bucket.length; i++) {
            // 剪枝
            if (bucket[i] + nums[index] > target) {
                continue;
            }

            // 装入桶
            bucket[i] += nums[index];

            // 递归 nums中的下一个数
            if (backtrace(nums, index + 1, bucket, target)) {
                return true;
            }

            // 从桶中移除
            bucket[i] -= nums[index];
        }

        return false;
    }
}

可通过对 nums[]数组的排序为从大到小的序列，使得更多的情况进入剪枝条件中

class Solution {
    public boolean canPartitionKSubsets(int[] nums, int k) {
        // 先排除一些乱七八糟的情况
        if (k > nums.length) {
            return false;
        }

        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (sum % k != 0) {
            return false;
        }

        Arrays.sort(nums);
        for (int i = 0, j = nums.length - 1; i < j; i++, j--) {
            int temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
        }

        int[] bucket = new int[k];
        int target = sum / k;
        return backtrace(nums, 0, bucket, target);
    }

    /**
     * 回溯遍历每一种可能，即会对每一个 nums中的元素进行 K次递归
     *
     * @param nums
     * @param index  表示当前是 nums中的第几个元素
     * @param bucket
     * @param target
     * @return
     */
    public boolean backtrace(int[] nums, int index, int[] bucket, int target) {
        // 如果所有元素都遍历完了
        if (index == nums.length) {
            // 检查每一个桶
            for (int i = 0; i < bucket.length; i++) {
                if (bucket[i] != target) {
                    return false;
                }
            }

            return true;
        }

        // 穷举 nums[i]可能装入的桶
        for (int i = 0; i < bucket.length; i++) {
            // 剪枝
            if (bucket[i] + nums[index] > target) {
                continue;
            }

            // 装入桶
            bucket[i] += nums[index];

            // 递归 nums中的下一个数
            if (backtrace(nums, index + 1, bucket, target)) {
                return true;
            }

            // 从桶中移除
            bucket[i] -= nums[index];
        }

        return false;
    }
}

从 桶的视角 进行回溯

class Solution {
    public boolean canPartitionKSubsets(int[] nums, int k) {
        // 先排除一些乱七八糟的情况
        if (k > nums.length) {
            return false;
        }

        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if (sum % k != 0) {
            return false;
        }

        boolean[] used = new boolean[nums.length];
        int target = sum / k;
        return backtrack(k, 0, nums, 0, used, target);

    }

    /**
     * @param k 当前还剩 
     * @param sum 当前桶盛放元素的和
     * @param nums
     * @param start 现在递归到了 nums中的哪个元素
     * @param used
     * @param target
     * @return
     */
    public boolean backtrack(int k, int sum, int[] nums, int start, boolean[] used, int target) {
        // 如果所有桶都被装满了，并且 nums一定都用完了
        if (k == 0) {
            return true;
        }

        // 如果当前桶被装满了，就递归下一个桶
        if (sum == target) {
            return backtrack(k - 1, 0, nums, 0, used, target);
        }

        for (int i = start; i < nums.length; i++) {
            // 剪枝，该数字已经被用过了
            if (used[i]) {
                continue;
            }

            // 剪枝，桶装不下 nums[i]
            if (nums[i] + sum > target) {
                continue;
            }

            // 将 nums[i]装入桶中
            used[i] = true;
            sum += nums[i];

            if (backtrack(k, sum, nums, i + 1, used, target)) {
                return true;
            }

            // 撤销
            used[i] = false;
            sum -= nums[i];
        }

        return false;
    }
}

[701] 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回 任意有效的结果 。

示例 1：
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：
示例 2：
输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]
示例 3：
输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]
提示：

给定的树上的节点数介于 0 和 10^4 之间

每个节点都有一个唯一整数值，取值范围从 0 到 10^8

-10^8 <= val <= 10^8

新值和原始二叉搜索树中的任意节点值都不同

Related Topics

树

二叉搜索树

二叉树

解法一：

通过 root.val 和 val之间的比较，确定待插入节点的位置，如果不需要插入，就把当前节点返回，不影响原树的结构

详见 day12: 二叉搜索树基础

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        if (root.val < val) {
            root.right = insertIntoBST(root.right, val);
        } else if (root.val > val) {
            root.left = insertIntoBST(root.left, val);
        }
        return root;
    }
}

解法二：

迭代

使用 while循环代替递归栈

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        TreeNode tmp = root;
        while (tmp != null) {
            if (val < tmp.val) {
                if (tmp.left == null) {
                    tmp.left = new TreeNode(val);
                    break;
                }
                tmp = tmp.left;
            } else {
                if (tmp.right == null) {
                    tmp.right = new TreeNode(val);
                    break;
                }
                tmp = tmp.right;
            }
        }

        return root;
    }
}

[712] 两个字符串的最小 ASCII删除和

给定两个字符串s1 和 s2，返回 使两个字符串相等所需删除字符的 ASCII 值的最小和 。

示例 1:

输入: s1 = "sea", s2 = "eat"
输出: 231
解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。
在 "eat" 中删除 "t" 并将 116 加入总和。
结束时，两个字符串相等，115 + 116 = 231 就是符合条件的最小和。

示例 2:

输入: s1 = "delete", s2 = "leet"
输出: 403
解释: 在 "delete" 中删除 "dee" 字符串变成 "let"，
将 100[d]+101[e]+101[e] 加入总和。在 "leet" 中删除 "e" 将 101[e] 加入总和。
结束时，两个字符串都等于 "let"，结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 "lee" 或 "eet"，我们会得到 433 或 417 的结果，比答案更大。

提示:

0 <= s1.length, s2.length <= 1000
s1 和 s2 由小写英文字母组成

Related Topics

字符串

动态规划

解法一：

基本同 [583]寻找两个字符串的删除操作

只是因为这道题要求计算具体删掉的最小字符的 ASCII总和，所以不能使用最长子序列的解法

class Solution {
    public int minimumDeleteSum(String s1, String s2) {
        int row = s1.length();
        int col = s2.length();
        int[][] dp = new int[row + 1][col + 1];
        // 当一个串是空的时候，ASCII和即为另一个的 i长度的字符总和
        for (int i = 1; i <= row; i++) {
            dp[i][0] = dp[i - 1][0] + s1.charAt(i - 1);
        }

        for (int i = 1; i <= col; i++) {
            dp[0][i] = dp[0][i - 1] + s2.charAt(i - 1);
        }

        // 值相等的时候，关系不变；不等的时候举个例子画一下，就能猜出来关系
        for (int i = 1; i <= row; i++) {
            char c1 = s1.charAt(i - 1);
            for (int j = 1; j <= col; j++) {
                char c2 = s2.charAt(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i][j - 1] + c2, dp[i - 1][j] + c1);
                }
            }
        }

        return dp[row][col];
    }
}

第二次手写

class Solution {
    public int minimumDeleteSum(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];

        for(int i = 1; i <= word1.length(); i++) {
            dp[i][0] = word1.charAt(i-1) + dp[i-1][0];
        }
        for(int i = 1; i <= word2.length(); i++) {
            dp[0][i] = (int)word2.charAt(i-1) + dp[0][i-1];
        }

        for(int i = 1; i <= word1.length(); i++) {
            for(int j = 1; j <= word2.length(); j++) {
                if (word1.charAt(i - 1) == word2.charAt(j-1)) {
                    dp[i][j] = dp[i-1][j-1];
                } else {
                    dp[i][j] = Math.min(dp[i-1][j] + word1.charAt(i-1), dp[i][j-1] + word2.charAt(j-1));
                }
            }
        }

        return dp[word1.length()][word2.length()];
    }
}

[714] 买卖股票最佳时机含手续费

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1：
输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:  
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
示例 2：
输入：prices = [1,3,7,5,10,3], fee = 3
输出：6
提示：

1 <= prices.length <= 5 * 104

1 <= prices[i] < 5 * 104

0 <= fee < 5 * 104

Related Topics

贪心

数组

动态规划

解法一：

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int buy = Integer.MIN_VALUE;
        int sell = 0;

        for(int x : prices) {
            buy = Math.max(buy, sell - x);
            sell = Math.max(sell, buy + x - fee);
        }

        return sell;
    }
}

[739] 每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示：

1 <= temperatures.length <= 105

30 <= temperatures[i] <= 100

Related Topics

栈

数组

单调栈

解法一：

单调栈

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        // 单调栈，存索引
        Stack<Integer> stack = new Stack<>();
        int[] res = new int[temperatures.length];

        for(int i = temperatures.length - 1; i >= 0; i--) {
            // 根据索引取数组中的值进行比较
            while(!stack.isEmpty() && temperatures[stack.peek()] <= temperatures[i]) {
                stack.pop();
            }
            // 记录当天是距今的第 x 天，要减一下
            res[i] = stack.isEmpty() ? 0 : stack.peek() - i;
            stack.push(i);
        }
        return res;
    }
}

[743] 网络延迟时间

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过有向边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

示例 1：
输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2
示例 2：
输入：times = [[1,2,1]], n = 2, k = 1
输出：1
示例 3：
输入：times = [[1,2,1]], n = 2, k = 2
输出：-1
提示：

1 <= k <= n <= 100

1 <= times.length <= 6000

times[i].length == 3

1 <= ui, vi <= n

ui != vi

0 <= wi <= 100

所有 (ui, vi) 对都 互不相同（即，不含重复边）

Related Topics

深度优先搜索

广度优先搜索

图

最短路

堆（优先队列）

解法一：

Dijkstra

class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        // 构造图
        List<int[]>[] graph = build(times, n);

        // 通过 dijkstra算法计算从 k点到其他各点的最小距离
        int[] distTo = dijkstra(k - 1, graph);

        // 找到最长的那条路径
        int res = 0;
        for (int dist : distTo) {
            // 存在节点不可达
            if (dist == Integer.MAX_VALUE) {
                return -1;
            }

            res = Math.max(res, dist);
        }
        return res;
    }

    private List<int[]>[] build(int[][] times, int n) {
        List<int[]>[] graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }

        for (int[] time : times) {
            int from = time[0] - 1;
            int to = time[1] - 1;
            int cost = time[2];
            graph[from].add(new int[]{
                    to, cost
            });
        }

        return graph;
    }

    class State {
        int id;
        int distFromStart;

        public State(int id, int distFromStart) {
            this.id = id;
            this.distFromStart = distFromStart;
        }
    }

    private int[] dijkstra(int k, List<int[]>[] graph) {
        // dp table，记录该路径下的最小权重值
        int[] distTo = new int[graph.length];
        Arrays.fill(distTo, Integer.MAX_VALUE);
        distTo[k] = 0;

        // 优先级队列的使用，可以保证在 while循环中每次获取的都是最近的点
        Queue<State> queue = new PriorityQueue<>((a, b) -> {
            return a.distFromStart - b.distFromStart;
        });

        queue.offer(new State(k, 0));
        while (!queue.isEmpty()) {
            State cur = queue.poll();
            int curId = cur.id;
            int curDist = cur.distFromStart;

            if (curDist > distTo[curId]) {
                continue;
            }

            for (int[] node : graph[curId]) {
                int nxtId = node[0];
                // 当前节点到相邻节点的一条边的距离
                int edgDist = node[1];
                int nxtDist = edgDist + distTo[curId];

                // 如果本次迭代得到的值更下，就要更新 dp table，并且以该节点为基础重新遍历其周围相邻节点
                if (distTo[nxtId] > nxtDist) {
                    distTo[nxtId] = nxtDist;
                    queue.offer(new State(nxtId, nxtDist));
                }
            }
        }

        return distTo;
    }
}

[752] 打开转盘锁

你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字： '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转：例如把 '9' 变为 '0'，'0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 '0000' ，一个代表四个拨轮的数字的字符串。

列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

字符串 target 代表可以解锁的数字，你需要给出解锁需要的最小旋转次数，如果无论如何不能解锁，返回 -1 。

示例 1:

输入：deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出：6
解释：
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的，
因为当拨动到 "0102" 时这个锁就会被锁定。

示例 2:

输入: deadends = ["8888"], target = "0009"
输出：1
解释：
把最后一位反向旋转一次即可 "0000" -> "0009"。

示例 3:

输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出：-1
解释：
无法旋转到目标数字且不被锁定。

示例 4:

输入: deadends = ["0000"], target = "8888"
输出：-1

提示：

1 <= deadends.length <= 500
deadends[i].length == 4
target.length == 4
target 不在 deadends 之中
target 和 deadends[i] 仅由若干位数字组成

Related Topics

广度优先搜索

数组

哈希表

字符串

解法一：

BFS

从 0000开始进行 BFS操作，针对每个字符，都可能有两种操作，所以一次变化会有 8种可能，如此可以构成一张图

详见 day13: BFS搜索算法

class Solution {
    public int openLock(String[] deadends, String target) {

        // 记录需要跳过的死亡代码
        Set<String> deads = new HashSet<>();
        for (String deadend : deadends) {
            deads.add(deadend);
        }

        // 记录已走过的路程，避免重复
        Set<String> visited = new HashSet<>();

        int step = 0;
        Queue<String> queue = new LinkedList<>();
        queue.offer("0000");
        visited.add("0000");

        while (!queue.isEmpty()) {

            int size = queue.size();

            for (int i = 0; i < size; i++) {
                String s = queue.poll();

                if (deads.contains(s)) {
                    continue;
                }

                if (s.equals(target)) {
                    return step;
                }

                // 当前一共有 4位字符
                for (int j = 0; j < 4; j++) {
                    String s1 = plusOne(s, j);
                    if (!visited.contains(s1)) {
                        visited.add(s1);
                        queue.offer(s1);
                    }
                    String s2 = minusOne(s, j);
                    if (!visited.contains(s2)) {
                        visited.add(s2);
                        queue.offer(s2);
                    }
                }
            }

            step++;*/
        }
        return -1;
    }

    public String plusOne(String s, int j) {
        char[] arr = s.toCharArray();
        if (arr[j] == '9') {
            arr[j] = '0';
        } else {
            arr[j] += 1;
        }

        return new String(arr);
    }

    public String minusOne(String s, int j) {
        char[] arr = s.toCharArray();
        if (arr[j] == '0') {
            arr[j] = '9';
        } else {
            arr[j] -= 1;
        }

        return new String(arr);
    }
}

也可以进行 双端 BFS

class Solution {
    public int openLock(String[] deadends, String target) {

        // 记录需要跳过的死亡代码
        Set<String> deads = new HashSet<>();
        for (String deadend : deadends) {
            deads.add(deadend);
        }

        Set<String> q1 = new HashSet<>();
        Set<String> q2 = new HashSet<>();
        Set<String> visited = new HashSet<>();

        q1.add("0000");
        q2.add(target);
        int step = 0;

        while (!q1.isEmpty() && !q2.isEmpty()) {
            Set<String> temp = new HashSet<>();
            for (String s : q1) {
                if (deads.contains(s)) {
                    continue;
                }
                if (q2.contains(s)) {
                    return step;
                }
                visited.add(s);

                for (int i = 0; i < 4; i++) {
                    String up = plusOne(s, i);
                    if (!visited.contains(up))
                        temp.add(up);
                    String down = minusOne(s, i);
                    if (!visited.contains(down))
                        temp.add(down);
                }
            }

            step++;
            q1 = q2;
            q2 = temp;
        }
        return -1;
    }

    public String plusOne(String s, int j) {
        char[] arr = s.toCharArray();
        if (arr[j] == '9') {
            arr[j] = '0';
        } else {
            arr[j] += 1;
        }

        return new String(arr);
    }

    public String minusOne(String s, int j) {
        char[] arr = s.toCharArray();
        if (arr[j] == '0') {
            arr[j] = '9';
        } else {
            arr[j] -= 1;
        }

        return new String(arr);
    }
}

[785] 判断二分图

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
示例 2：
输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3：
输入：numCourses = 1, prerequisites = []
输出：[0]
提示：

1 <= numCourses <= 2000

0 <= prerequisites.length <= numCourses * (numCourses - 1)

prerequisites[i].length == 2

0 <= ai, bi < numCourses

ai != bi

所有[ai, bi] 互不相同

Related Topics

深度优先搜索

广度优先搜索

图

拓扑排序

解法一：

DFS

注意：因为图不一定连通，所以需要在 main函数中就 for循环 traverse()

class Solution {
    boolean visited[];
    boolean color[];
    boolean flag = true;

    public boolean isBipartite(int[][] graph) {
        visited = new boolean[graph.length];
        color = new boolean[graph.length];
        // 图不一定连通，如果已经不是二分图了，就不递归了
        for (int i = 0; i < graph.length && flag; i++) {
            if (!visited[i]) {
                traverse(graph, i);
            }
        }
        return flag;
    }

    private void traverse(int[][] graph, int idx) {
        // 到访标记
        visited[idx] = true;
        // 遍历所有出度节点
        for (int v : graph[idx]) {
            // 如果没访问过，就染色
            if (!visited[v]) {
                color[v] = !color[idx];
                traverse(graph, v);
                // 如果访问过了，就比较
            } else {
                if (color[v] == color[idx]) {
                    flag = false;
                    return;
                }
            }
        }
    }
}

解法二：

BFS

class Solution {
    boolean flag = true;
    boolean[] visited;
    boolean[] color;

    public boolean isBipartite(int[][] graph) {
        visited = new boolean[graph.length];
        color = new boolean[graph.length];
        Queue<Integer> queue = new LinkedList<>();

        for (int i = 0; i < graph.length && flag; i++) {
            if (!visited[i])
                traverse(graph, i, queue);
        }

        return flag;
    }

    private void traverse(int[][] graph, int idx, Queue<Integer> queue) {
        queue.offer(idx);
        visited[idx] = true;
        
        while (!queue.isEmpty()) {
            Integer cur = queue.poll();
            // 注意这里是 graph[cur]
            for (int v : graph[cur]) {
                // 颜色校验
                if (visited[v]) {
                    if (color[v] == color[cur]) {
                        flag = false;
                        return;
                    }
                    // 染色
                } else {
                    visited[v] = true;
                    color[v] = !color[cur];
                    queue.offer(v);
                }
            }
        }
    }
}

♥ [787] K站中转内最便宜的航班

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。如果不存在这样的路线，则输出 -1。

示例 1：
输入: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释: 
城市航班图如下


从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200，如图中红色所示。
示例 2：
输入: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出: 500
解释: 
城市航班图如下


从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500，如图中蓝色所示。
提示：

1 <= n <= 100

0 <= flights.length <= (n * (n - 1) / 2)

flights[i].length == 3

0 <= fromi, toi < n

fromi != toi

1 <= pricei <= 104

航班没有重复，且不存在自环

0 <= src, dst, k < n

src != dst

Related Topics

深度优先搜索

广度优先搜索

图

动态规划

最短路

堆（优先队列）

解法一：

不是特别理解

int[][] dp = new int[n][k+2]

dp[i][j]表示从 i开始走 j步到达 dst的费用和

所以可得递推式：dp[now][j] = Math.min(dp[now][j], dp[nxt][j-1] + cost)

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        // 最多有 100个节点，单条路径最大为 10000，所以反正就是一个很大的值就行了
        final int placeHolder = 1000001;
        int[][] dp = new int[n][k + 2];
        for (int i = 0; i < n; i++) {
            Arrays.fill(dp[i], placeHolder);
        }

        // 自己到自己的价格为 0
        dp[dst][0] = 0;
        
        // dp过程
        for (int i = 1; i < k + 2; i++) {
            for (int[] flight : flights) {
                int now = flight[0], nxt = flight[1], cost = flight[2];
                dp[now][i] = Math.min(dp[now][i], dp[nxt][i - 1] + cost);
            }
        }

        // 计算 dp[src]那一行中的最小值
        int ans = Arrays.stream(dp[src]).min().getAsInt();
        return ans == placeHolder ? -1 : ans;
    }
}

[797] 所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2：
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
提示：

n == graph.length

2 <= n <= 15

0 <= graph[i][j] < n

graph[i][j] != i（即不存在自环）

graph[i] 中的所有元素 互不相同

保证输入为 有向无环图（DAG）

Related Topics

深度优先搜索

广度优先搜索

图

回溯

解法一：

回溯

class Solution {
    List<List<Integer>> res;

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        res = new LinkedList<>();
        // 记录当时已遍历的节点
        LinkedList<Integer> path = new LinkedList<>();
        traverse(graph, 0, path);
        return res;
    }

    private void traverse(int[][] graph, int idx, LinkedList<Integer> path) {
        /*
            注意：对于图的遍历，记录和删除一般都放在 for循环外；如果在里头就会丢失第一次遍历的根节点的值
        */
        // 记录
        path.addLast(idx);
        int n = graph.length;

        if (idx == n - 1) {
            res.add(new LinkedList<>(path));
            // 删除
            path.removeLast();
            return;
        }

        for (int c : graph[idx]) {
            traverse(graph, c, path);
        }

        // 删除
        path.removeLast();
    }
}

[875] 爱吃香蕉的珂珂

珂珂喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。

珂珂可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

示例 1：
输入: piles = [3,6,7,11], H = 8
输出: 4
示例 2：
输入: piles = [30,11,23,4,20], H = 5
输出: 30
示例 3：
输入: piles = [30,11,23,4,20], H = 6
输出: 23
提示：

1 <= piles.length <= 10^4

piles.length <= H <= 10^9

1 <= piles[i] <= 10^9

Related Topics

数组

二分查找

解法一：

二分查找

先明确单调的函数式，然后进行二分查找

具体的看 day6: 二分搜索应用

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int left = 1, right = 0;
        for (int pile : piles) {
            right = right > pile ? right : pile;
        }
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (f(piles, mid) == h) {
                right = mid - 1;
            } else if (f(piles, mid) < h) {
                right = mid - 1;
            } else if (f(piles, mid) > h) {
                left = mid + 1;
            }
        }

        return left;
    }

    /**
     * 需要吃完所有香蕉的时间
     *
     * @param piles
     * @param x
     * @return
     */
    int f(int[] piles, int x) {
        int hours = 0;
        for (int i = 0; i < piles.length; i++) {
            hours += piles[i] / x;
            if (piles[i] % x > 0) {
                hours++;
            }
        }

        return hours;
    }
}

第二次手写

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int left = 1, right = 0;
        for (int x : piles) {
            right = Math.max(right, x);
        }

        while (left < right) {
            int mid = left + (right - left) / 2;
            if (f(mid, piles) == h) {
                right = mid;
            } else if (f(mid, piles) > h) {
                left = mid + 1;
            } else if (f(mid, piles) < h) {
                right = mid;
            }
        }

        return left;
    }

    private int f(int speed, int[] piles) {
        int time = 0;
        for (int x : piles) {
            if (x <= speed) {
                time++;
            } else if (x > speed) {
                time += x / speed;
                time += (x % speed == 0) ? 0 : 1;
            }
        }

        return time;
    }
}

[886] 可能的二分法

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

不存在自环（graph[u] 不包含 u）。
不存在平行边（graph[u] 不包含重复值）。
如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例 1：
输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。
示例 2：
输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。
提示：

graph.length == n

1 <= n <= 100

0 <= graph[u].length < n

0 <= graph[u][i] <= n - 1

graph[u] 不会包含 u

graph[u] 的所有值 互不相同

如果 graph[u] 包含 v，那么 graph[v] 也会包含 u

Related Topics

深度优先搜索

广度优先搜索

并查集

图

解法一：

DFS

先构建图，然后判断是否是二分图

class Solution {
    boolean[] color;
    boolean[] visited;
    boolean flag = true;

    public boolean possibleBipartition(int n, int[][] dislikes) {
        color = new boolean[n];
        visited = new boolean[n];
        // 构建图
        List<Integer>[] graph = build(n, dislikes);
        for (int i = 0; i < n && flag; i++) {
            if (!visited[i])
                traverse(graph, i);
        }
        return flag;
    }

    private void traverse(List<Integer>[] graph, int idx) {
        // 别忘了这步
        visited[idx] = true;
        for (int v : graph[idx]) {
            if (visited[v]) {
                if (color[v] == color[idx]) {
                    flag = false;
                    return;
                }
            } else {
                color[v] = !color[idx];
                traverse(graph, v);
            }
        }
    }

    private List<Integer>[] build(int n, int[][] dislikes) {
        List<Integer>[] graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }

        // 注意是无向图，所以两个节点都要加
        for (int[] arr : dislikes) {
            graph[arr[0] - 1].add(arr[1] - 1);
            graph[arr[1] - 1].add(arr[0] - 1);
        }

        return graph;
    }
}

[912] 排序数组

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：
输入：nums = [5,2,3,1]
输出：[1,2,3,5]
示例 2：
输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]
提示：

1 <= nums.length <= 5 * 104

-5 * 104 <= nums[i] <= 5 * 104

Related Topics

数组

分治

桶排序

计数排序

基数排序

排序

堆（优先队列）

归并排序

解法一：

归并排序

class Solution {
    int[] tmp;
    public int[] sortArray(int[] nums) {
        tmp = new int[nums.length] ;
        sort(nums, 0, nums.length - 1);
        return nums;
    }

    private void sort(int[] nums, int left, int right) {
        if (left >= right) {
            return;
        }

        int mid = left + (right - left) / 2;
        // 先一直拆分
        sort(nums, left, mid);
        sort(nums, mid + 1, right);
        // 归并
        merge(nums, left, mid, right);
    }

    private void merge(int[] nums, int left, int mid, int right) {
        // 先将数据拷贝到临时数组中，然后双指针判断，类似链表合并
        for(int i = left; i <= right; i++) {
            tmp[i] = nums[i];
        }

        int p = left, q = mid + 1;
        for(int i = left; i <= right; i++) {
            if (p >= mid + 1) {
                nums[i] = tmp[q++];
            } else if (q >= right + 1) {
                nums[i] = tmp[p++];
            } else if (tmp[p] > tmp[q]) {
                nums[i] = tmp[q++];
            } else {
                nums[i] = tmp[p++];
            }
        }
    }
}

解法二：

快排

因为快排是不稳定的，因此为了避免它变成 O(n²)，可以先对其进行打乱

class Solution {
    public int[] sortArray(int[] nums) {
        // 打乱数组
        shuffle(nums);
        sort(nums, 0, nums.length - 1);
        return nums;
    }

    private void shuffle(int[] nums) {
        Random random = new Random();
        for(int i = 0; i < nums.length; i++) {
            swap(nums, i, random.nextInt(nums.length));
        }
    }


    private void sort(int[] nums, int left, int right) {
        if (left >= right) {
            return;
        }

        // 先为 nums[left]找到一个合适的位置，位置就是 p
        // 此时，可以明确的一点就是，nums[1 .. p-1] <= nums[p] <= nums[p+1 .. length - 1]
        int p = partition(nums, left, right);
        sort(nums, left, p-1);
        sort(nums, p+1, right);
    }

    private int partition(int[] nums, int left, int right) {
        int pivot = left;
        int i = left, j = right;
        while(i <= j) {
            // 向右寻找第一个比 pivot大的数
            while(i < right && nums[i] <= nums[pivot]) {
                i++;
            }
            // 向左寻找第一个比 pivot小的数
            while (j > left && nums[j] > nums[pivot]) {
                j--;
            }
            // i 和 j是从两头过来的，当 i >= j成立时，就说明对该数组的第一次遍历完成
            if (i >= j) {
                break;
            }
            swap(nums, i, j);
        }
        // 因为要把小的数左移，所以这里要和 j交换位置
        swap(nums, pivot, j);
        return j;
    }

    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

[931] 下降路径最小和

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径
示例 2：
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径
提示：

n == matrix.length == matrix[i].length

1 <= n <= 100

-100 <= matrix[i][j] <= 100

Related Topics

数组

动态规划

矩阵

解法一：

直接在原数组 matrix上进行 dp，matrix[i][j] = Math.min(matrix[i-1][j-1], matrix[i-1][j], matrix[i-1][j+1])

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int len = matrix.length;

        for (int i = 1; i < len; i++) {
            for (int j = 0; j < len; j++) {
                if (j == 0) {
                    int add = Math.min(matrix[i - 1][j], matrix[i - 1][j + 1]);
                    matrix[i][j] += add;
                } else if (j == len - 1) {
                    int add = Math.min(matrix[i - 1][j], matrix[i - 1][j - 1]);
                    matrix[i][j] += add;
                } else {
                    int add = Math.min(matrix[i - 1][j], matrix[i - 1][j + 1]);
                    add = Math.min(matrix[i - 1][j - 1], add);
                    matrix[i][j] += add;
                }
            }
        }

        int res = Integer.MAX_VALUE;
        for (int i = 0; i < len; i++) {
            res = Math.min(matrix[len - 1][i], res);
        }
        return res;
    }
}

当然，也可以再进行空间压缩，只用一个一维数组 int[] arr = new int[len]，记录到当前层为止的值；

并且每次计算的时候，arr[i]覆盖 arr[i]，刚好还能取到上一次在这里的值

第二次手写

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int[][] dp = new int[matrix.length][matrix.length];
        for(int i = 0; i < matrix.length; i++) {
            dp[0][i] = matrix[0][i];
        }

        for(int i = 1; i < matrix.length; i++) {
            for(int j = 0; j < matrix.length; j++) {
                int val = dp[i-1][j];
                if (j > 0) {
                    val = Math.min(val, dp[i-1][j-1]);
                }
                if (j < matrix.length - 1) {
                    val = Math.min(val, dp[i-1][j+1]);
                }
                dp[i][j] = val + matrix[i][j];
            }
        }

        int min = Integer.MAX_VALUE;
        for(int i = 0; i < matrix.length; i++) {
            min = Math.min(dp[matrix.length - 1][i], min);
        }
        return min;
    }
}

[990] 等式方程的可满足性

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一："a==b" 或 "a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

示例 1：
输入：["a==b","b!=a"]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。
示例 2：
输入：["b==a","a==b"]
输出：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。
示例 3：
输入：["a==b","b==c","a==c"]
输出：true
示例 4：
输入：["a==b","b!=c","c==a"]
输出：false
示例 5：
输入：["c==c","b==d","x!=z"]
输出：true
提示：

1 <= equations.length <= 500

equations[i].length == 4

equations[i][0] 和 equations[i][3] 是小写字母

equations[i][1] 要么是 '='，要么是 '!'

equations[i][2] 是 '='

Related Topics

并查集

图

数组

字符串

解法一：

并查集

先对所有的 ==式子进行操作，把其中的元素都连通起来

然后对 !=式子进行操作，如果其中的元素存在连通就返回 false

注意，因为最多有 26个字母，所以数组长度可设置为 26，并且为了方便获取，可以让 每个元素 - ‘a’

详见 day14: 并查集（Union-Find）算法

class Solution {
    public boolean equationsPossible(String[] equations) {
        // 定义并查集
        UF uf = new UF();

        // 遍历等式方程
        for (String k : equations) {
            // 获取 参数1
            char a = k.charAt(0);
            // 获取 参数2
            char b = k.charAt(3);
            // 判断是 == 还是 !=
            char c = k.charAt(1);
            // 如果是 ==，就为参数1 和 参数2创建连接
            if (c != '!') {
                uf.union(a - 'a', b - 'a');
            }
        }

        // 再度遍历等式方程
        for (String k : equations) {
            char a = k.charAt(0);
            char b = k.charAt(3);
            char c = k.charAt(1);
            // 如果是 !=，那么参数1和参数2就不应该连接
            if (c == '!') {
                // 如果连接了，就返回 false
                if (uf.connected(a - 'a', b - 'a')) {
                    return false;
                }
            }
        }
        return true;
    }
}

class UF {
    // 使用数组存储树
    int[] parent;
    // 记录树的重量，方便在进行连通时，创造高度尽可能低的树
    int[] size;

    public UF() {
        parent = new int[26];
        size = new int[26];
        // 初始化数组
        for (int i = 0; i < 26; i++) {
            // 初始时，每棵树的父节点是它自己，因为每个节点都是独立的
            parent[i] = i;
            size[i] = 1;
        }
    }

    /**
     * 连通两棵树
     *
     * @param a
     * @param b
     */
    public void union(int a, int b) {
        // 找到两个节点的最顶层根节点
        int q = find(a);
        int p = find(b);

        // 如果根节点相同，说明已经连通了
        if (q == b) {
            return;
        }

        // 否则根据两颗树的重量，决定是左树加入到右树中，还是右树加入到左树中
        if (size[p] > size[q]) {
            parent[q] = p;
            // 更新树的重量
            size[p] += size[q];
        } else {
            parent[p] = q;
            size[q] += size[p];
        }
    }

    /**
     * 找到一个节点的根节点
     *
     * @param a
     * @return
     */
    public int find(int a) {
        while (a != parent[a]) {
            // 进行路径压缩，能以 O(1)的复杂度找到根节点
            parent[a] = parent[parent[a]];
            a = parent[a];
        }
        return a;
    }

    /**
     * 判断两个节点是否连通，即是不是在同一棵树内
     *
     * @param a
     * @param b
     * @return
     */
    public boolean connected(int a, int b) {
        return find(a) == find(b);
    }
}

[1094] 拼车

假设你是一位顺风车司机，车上最初有 capacity 个空座位可以用来载客。由于道路的限制，车只能向一个方向行驶（也就是说，不允许掉头或改变方向，你可以将其想象为一个向量）。

这儿有一份乘客行程计划表 trips[][]，其中 trips[i] = [num_passengers, start_location, end_location] 包含了第 i 组乘客的行程信息：

必须接送的乘客数量；
乘客的上车地点；
以及乘客的下车地点。

这些给出的地点位置是从你的初始出发位置向前行驶到这些地点所需的距离（它们一定在你的行驶方向上）。

请你根据给出的行程计划表和车子的座位数，来判断你的车是否可以顺利完成接送所有乘客的任务（当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false）。

示例 1：
输入：trips = [[2,1,5],[3,3,7]], capacity = 4
输出：false
示例 2：
输入：trips = [[2,1,5],[3,3,7]], capacity = 5
输出：true
示例 3：
输入：trips = [[2,1,5],[3,5,7]], capacity = 3
输出：true
示例 4：
输入：trips = [[3,2,7],[3,7,9],[8,3,9]], capacity = 11
输出：true
提示：

你可以假设乘客会自觉遵守 “先下后上” 的良好素质

trips.length <= 1000

trips[i].length == 3

1 <= trips[i][0] <= 100

0 <= trips[i][1] < trips[i][2] <= 1000

1 <= capacity <= 100000

Related Topics

数组

前缀和

排序

模拟

堆（优先队列）

解法一：

差分数组，也就是前缀和的变式，把在不同站点的上下车看作是对差分数组不同区间内的数的加减操作。

最后计算每一个站点的人数，如果人数超标就返回 false，并且因为只需要进行判断，所以人数可以不用数组来存（或者说，人数不需要存）

class Solution {
    public boolean carPooling(int[][] trips, int capacity) {

        // 计算最长有多少个站点
        int len = 0;
        for (int[] trip : trips) {
            len = len > trip[2] ? len : trip[2];
        }

        // 声明差分数组
        int[] diff = new int[len + 1];
        // 声明某个站点的人数
        int res;
        
        // 初始化差分数组
        for (int[] trip : trips) {
            int di = trip[0];
            int i = trip[1];
            int j = trip[2];

            diff[i] += di;
            // 因为默认是先下车后上车的，所以这里是 diff[j]而不是 diff[j+1]
            diff[j] -= di;
        }

        // 计算每个站点的人数并返回结果
        res = diff[0];
        for (int i = 1; i < diff.length; i++) {
            if (res > capacity) {
                return false;
            }
            res += diff[i];
        }
        return true;
    }
}

[1011] 在 D天内送达包裹的能力

传送带上的包裹必须在 D 天内从一个港口运送到另一个港口。

传送带上的第 i 个包裹的重量为 weights[i]。每一天，我们都会按给出重量的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。

返回能在 D 天内将传送带上的所有包裹送达的船的最低运载能力。

示例 1：

输入：weights = [1,2,3,4,5,6,7,8,9,10], D = 5
输出：15
解释：
船舶最低载重 15 就能够在 5 天内送达所有包裹，如下所示：
第 1 天：1, 2, 3, 4, 5
第 2 天：6, 7
第 3 天：8
第 4 天：9
第 5 天：10

请注意，货物必须按照给定的顺序装运，因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。

示例 2：

输入：weights = [3,2,2,4,1,4], D = 3
输出：6
解释：
船舶最低载重 6 就能够在 3 天内送达所有包裹，如下所示：
第 1 天：3, 2
第 2 天：2, 4
第 3 天：1, 4

示例 3：

输入：weights = [1,2,3,1,1], D = 4
输出：3
解释：
第 1 天：1
第 2 天：2
第 3 天：3
第 4 天：1, 1

提示：

1 <= D <= weights.length <= 5 * 104
1 <= weights[i] <= 500

Related Topics

贪心

数组

二分查找

解法一：

二分查找

具体解释看 day6: 二分搜索运用

class Solution {


    public int shipWithinDays(int[] weights, int days) {

        // 申明二分查找的左右边界
        int left = 0, right = 0;

        // 遍历 weights数组，为左右边界赋值
        for (int weight : weights) {
            left = Math.max(left, weight);
            right += weight;
        }

        // 进行二分查找，找到最合适的左边界
        while (left <= right) {
            int mid = left + (right - left) / 2;
            int fDay = f(mid, weights);
            if (fDay <= days) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

    /**
     * 获取当前载重状态下的天数
     *
     * @param weight
     * @param nums
     * @return
     */
    public int f(int weight, int[] nums) {
        int day = 0;
        int sum = 0;

        // 遍历所有货物的重量
        for (int i = 0; i < nums.length; i++) {
            // 如果当前重量和 加上下一个货物超重了，就说明这一天只能装载 sum重的货物，之后将 sum重置
            if ((sum + nums[i]) > weight) {
                day++;
                sum = 0;
            }
            sum += nums[i];
        }

        // 最后一天需要再 + 1，注意别 return day++，那样是先返回再 ++的，（我是傻逼）
        day++;
        return day;
    }
}

第二次手写

class Solution {
    public int shipWithinDays(int[] weights, int days) {
        int left = 0, right = 0;
        for(int x : weights) {
            left = Math.max(left, x);
            right += x;
        }

        while(left < right) {
            int mid = left + (right - left) / 2;
            if (f(mid, weights) == days) {
                right = mid;
            } else if (f(mid, weights) < days) {
                right = mid;
            } else if (f(mid, weights) > days) {
                left = mid + 1;
            }
        }

        return left;
    }

    private int f(int capacity, int[] weights) {
        int cnt = 0;
        int sum = 0;
        for(int x : weights) {
            if (sum <= capacity && sum + x > capacity) {
                cnt++;
                sum = 0;
            }
            sum += x;
        }
        // 第二次手写的时候，把这个忘记了
        // 如果最后一截不满足 sum + x >capacity，那么就不会触发 cnt++，就必须再最后再 ++
        cnt++;
        return cnt;
    }
}

[1024] 视频拼接

你将会获得一系列视频片段，这些片段来自于一项持续时长为 time 秒的体育赛事。这些片段可能有所重叠，也可能长度不一。

使用数组 clips 描述所有的视频片段，其中 clips[i] = [starti, endi] 表示：某个视频片段开始于 starti 并于 endi 结束。

甚至可以对这些片段自由地再剪辑：

例如，片段 [0, 7] 可以剪切成 [0, 1] + [1, 3] + [3, 7] 三部分。

我们需要将这些片段进行再剪辑，并将剪辑后的内容拼接成覆盖整个运动过程的片段（[0, time]）。返回所需片段的最小数目，如果无法完成该任务，则返回 -1 。

示例 1：

输入：clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], time = 10
输出：3
解释：
选中 [0,2], [8,10], [1,9] 这三个片段。
然后，按下面的方案重制比赛片段：
将 [1,9] 再剪辑为 [1,2] + [2,8] + [8,9] 。
现在手上的片段为 [0,2] + [2,8] + [8,10]，而这些覆盖了整场比赛 [0, 10]。

示例 2：

输入：clips = [[0,1],[1,2]], time = 5
输出：-1
解释：
无法只用 [0,1] 和 [1,2] 覆盖 [0,5] 的整个过程。

示例 3：

输入：clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], time = 9
输出：3
解释： 
选取片段 [0,4], [4,7] 和 [6,9] 。

示例 4：

输入：clips = [[0,4],[2,8]], time = 5
输出：2
解释：
注意，你可能录制超过比赛结束时间的视频。

提示：

1 <= clips.length <= 100
0 <= starti <= endi <= 100
1 <= time <= 100

Related Topics

贪心

数组

动态规划

解法一：

dp[i]表示覆盖从 0 ~ i 区间需要的最少的子区间数量

dp[i] = Math.min(dp[i], dp[nums[0]] + 1)

class Solution {
    public int videoStitching(int[][] clips, int time) {
        if (time == 0 || clips.length == 0) {
            return 0;
        }

        int[] dp = new int[time+1];
        Arrays.fill(dp, 101);
        // 啥都不覆盖，不需要片段，即为0
        dp[0] = 0;

        for(int i = 1; i <= time; i++) {
            for(int[] nums : clips) {
                if (i > nums[0] && i <= nums[1]) {
                    dp[i] = Math.min(dp[i], dp[nums[0]] + 1);
                }
            }
        }

        return dp[time] == 101 ? -1 : dp[time];
    }
}

[1109] 航班预定

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti （包含 firsti 和 lasti ）的 每个航班 上预订了 seatsi 个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

示例 1：

输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出：[10,55,45,25,25]
解释：
航班编号        1   2   3   4   5
预订记录 1 ：   10  10
预订记录 2 ：       20  20
预订记录 3 ：       25  25  25  25
总座位数：      10  55  45  25  25
因此，answer = [10,55,45,25,25]

示例 2：

输入：bookings = [[1,2,10],[2,2,15]], n = 2
输出：[10,25]
解释：
航班编号        1   2
预订记录 1 ：   10  10
预订记录 2 ：       15
总座位数：      10  25
因此，answer = [10,25]

提示：

1 <= n <= 2 * 104
1 <= bookings.length <= 2 * 104
bookings[i].length == 3
1 <= firsti <= lasti <= n
1 <= seatsi <= 104

Related Topics

数组

前缀和

解法一：

差分数组（前缀和的变种问题），基本同《拼车》问题，感觉还要再简单一点

class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {
        // 声明差分数组
        int[] diff = new int[n + 1];
        // 声明返回值数组
        int[] res = new int[n];

        // 构造差分数组
        for (int[] booking : bookings) {
            int i = booking[0];
            int j = booking[1];
            int seats = booking[2];

            diff[i - 1] += seats;
            diff[j] -= seats;
        }


        // 构造返回值数组
        res[0] = diff[0];
        for (int i = 1; i < res.length; i++) {
            res[i] = res[i - 1] + diff[i];
        }

        return res;
    }
}

同样用差分数组，但是不需要构造返回值数组了，直接在差分数组里面操作，并且差分数组的长度可以设置为 n，只是需要加一个 if判断

class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {
        int[] nums = new int[n];
        for (int[] booking : bookings) {
            nums[booking[0] - 1] += booking[2];
            // 加一个 if判断
            if (booking[1] < n) {
                nums[booking[1]] -= booking[2];
            }
        }
        // 直接在差分数组里进行操作
        for (int i = 1; i < n; i++) {
            nums[i] += nums[i - 1];
        }
        return nums;
    }
}

[1143] 最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：
输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。
示例 2：
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。
示例 3：
输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。
提示：

1 <= text1.length, text2.length <= 1000

text1 和 text2 仅由小写英文字符组成。

Related Topics

字符串

动态规划

解法一：

注意，序列并不要求连续

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int row = text1.length();
        int col = text2.length();
        // dp[i][j]:表示在字符串s[0...i]中和字符串s[0...j]中最长公共子序列的长度为dp[i][j]。
        int[][] dp = new int[row + 1][col + 1];

        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= col; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[row][col];
    }
}

[1584] 连接所有点的最小费用

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

示例 1：

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：

我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

示例 2：

输入：points = [[3,12],[-2,5],[-4,1]]
输出：18

示例 3：

输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4

示例 4：

输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000

示例 5：

输入：points = [[0,0]]
输出：0

提示：

1 <= points.length <= 1000
-106 <= xi, yi <= 106
所有点 (xi, yi) 两两不同。

Related Topics

并查集

数组

最小生成树

解法一：

并查集、Kruskal

使用并查集将两个节点连接到一起，然后使用优先级队列按照边的长度来存储边

class Solution {
    public int minCostConnectPoints(int[][] points) {
        if (points.length == 0 || points.length == 1) {
            return 0;
        }

        int res = 0;
        // 优先级队列
        PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> {
            return a[2] - b[2];
        });

		// 确定边长
        for (int i = 0; i < points.length; i++) {
            for (int j = i + 1; j < points.length; j++) {
                int len = Math.abs(points[i][0] - points[j][0]) + Math.abs(points[i][1] - points[j][1]);
                queue.offer(new int[]{i, j, len});
            }
        }
		// 并查集操作
        UF uf = new UF(points.length);
        while (!queue.isEmpty()) {
            int[] edg = queue.poll();
            int a = edg[0];
            int b = edg[1];
            int cost = edg[2];
            if (uf.connected(a, b)) {
                continue;
            }
            res += cost;
            uf.union(a, b);
        }

        return res;
    }

    // 并查集
    static class UF {
        int count;
        int[] parent;
        int[] size;

        public UF(int count) {
            this.count = count;
            parent = new int[count];
            size = new int[count];
            for (int i = 0; i < count; i++) {
                parent[i] = i;
                size[i] = 1;
            }
        }

        public int find(int idx) {
            while (parent[idx] != idx) {
                parent[idx] = parent[parent[idx]];
                idx = parent[idx];
            }
            return idx;
        }

        public boolean connected(int p, int q) {
            return find(p) == find(q);
        }

        public void union(int p, int q) {
            int r1 = find(p);
            int r2 = find(q);
            if (r1 == r2) {
                return;
            }

            if (size[r1] > size[r2]) {
                size[r1] += size[r2];
                parent[r2] = r1;
            } else {
                size[r2] += size[r1];
                parent[r1] = r2;
            }
        }

        public int count() {
            return count;
        }
    }
}

解法二：

Prim

class Solution {
    public int minCostConnectPoints(int[][] points) {
        // graph[i] 表示节点 i相邻的边集合，一条边由数组 int[]{本节点，目标节点，权重}组成
        List<int[]>[] graph = build(points);
        Prim prim = new Prim(graph);
        return prim.treeWeight();
    }

    // 构造图
    private List<int[]>[] build(int[][] points) {
        int len = points.length;
        List<int[]>[] graph = new List[len];
        for (int i = 0; i < len; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int i = 0; i < len; i++) {
            for (int j = i + 1; j < len; j++) {
                int weight = Math.abs(points[i][0] - points[j][0]) + Math.abs(points[i][1] - points[j][1]);
                // 无向图，可看作双向图
                graph[i].add(new int[]{i, j, weight});
                graph[j].add(new int[]{j, i, weight});
            }
        }
        return graph;
    }

    class Prim {
        // 记录横切边
        private PriorityQueue<int[]> queue;
        // 记录节点是否被纳入最小生成树
        private boolean[] visited;
        private int treeWeight = 0;
        private List<int[]>[] graph;

        public Prim(List<int[]>[] graph) {
            this.graph = graph;
            int len = graph.length;
            visited = new boolean[len];
            queue = new PriorityQueue<>(len, (a, b) -> a[2] - b[2]);
            // 先随便切一个
            visited[0] = true;
            cut(0);

            while (!queue.isEmpty()) {
                // 因为是优先级队列，所以每次得到的边都是最小的边，符合贪心算法
                int[] edg = queue.poll();
                int to = edg[1];
                int weight = edg[2];
                // 判断该边的目标节点（另一个节点）是否已被纳入最小生成树
                if (visited[to]) {
                    continue;
                }
                // 纳入
                visited[to] = true;
                treeWeight += weight;
                // 切分横切边
                cut(to);
            }

        }

        // 切分横切边
        private void cut(int idx) {
            for (int[] edg : graph[idx]) {
                int to = edg[1];
                // 主要就是将某个节点的邻边填入到优先级队列中
                // 如果该边连接的目标节点已被纳入最小生成树，就不填入该边
                if (visited[to]) {
                    continue;
                }
                queue.offer(edg);
            }
        }

        public Integer treeWeight() {
            return treeWeight;
        }

        public Boolean allConnected() {
            for (boolean b : visited) {
                if (!b) {
                    return false;
                }
            }
            return true;
        }
    }
}

[1650] 二叉树的最近公共祖先 Ⅲ

给定一棵二叉树中的两个节点 p 和 q，返回它们的最近公共祖先节点（LCA）。

每个节点都包含其父节点的引用（指针）。Node 的定义如下：

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

根据维基百科中对最近公共祖先节点的定义：“两个节点 p 和 q 在二叉树 T 中的最近公共祖先节点是后代节点中既包括 p 又包括 q 的最深节点（我们允许一个节点为自身的一个后代节点）”。一个节点 x 的后代节点是节点 x 到某一叶节点间的路径中的节点 y。

示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和 1 的最近公共祖先是 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和 4 的最近公共祖先是 5，根据定义，一个节点可以是自身的最近公共祖先。
示例 3:
输入: root = [1,2], p = 1, q = 2
输出: 1
提示:

树中节点个数的范围是 [2, 105]。

-109 <= Node.val <= 109

所有的 Node.val 都是互不相同的。

p != q

p 和 q 存在于树中。

Related Topics

树

哈希表

二叉树

解法一：

将二叉树想象成链表，就变成了求链表的交点

class Solution {
    public Node lowestCommonAncestor(Node p, Node q) {
        Node a = p, b = q;
        while (a != b) {
            // 注意这里是 if-else类型的，即a，b每次只能走一步！！！
            if (a == null) {
                a = q;
            } else {
                a = a.parent;
            }
            if (b == null) {
                b = p;
            } else {
                b = b.parent;
            }
        }

        return a;
    }
}

[1676] 二叉树的最近公共祖先 Ⅳ

给定一棵二叉树的根节点 root 和 TreeNode 类对象的数组（列表） nodes，返回 nodes 中所有节点的最近公共祖先（LCA）。数组（列表）中所有节点都存在于该二叉树中，且二叉树中所有节点的值都是互不相同的。

我们扩展二叉树的最近公共祖先节点在维基百科上的定义：“对于任意合理的 i 值， n 个节点 p1 、 p2、...、 pn 在二叉树 T 中的最近公共祖先节点是后代中包含所有节点 pi 的最深节点（我们允许一个节点是其自身的后代）”。一个节点 x 的后代节点是节点 x 到某一叶节点间的路径中的节点 y。

示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [4,7]
输出: 2
解释: 节点 4 和 7 的最近公共祖先是 2。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [1]
输出: 1
解释: 单个节点的最近公共祖先是该节点本身。
示例 3:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [7,6,2,4]
输出: 5
解释: 节点 7、6、2 和 4 的最近公共祖先节点是 5。
示例 4:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [0,1,2,3,4,5,6,7,8]
输出: 3
解释: 树中所有节点的最近公共祖先是根节点。
提示:

树中节点个数的范围是 [1, 104] 。

-109 <= Node.val <= 109

所有的 Node.val 都是互不相同的。

所有的 nodes[i] 都存在于该树中。

所有的 nodes[i] 都是互不相同的。

Related Topics

树

深度优先搜索

二叉树

解法一：

基本和 236一样

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode[] nodes) {
        return find(root, nodes);
    }

    private TreeNode find(TreeNode root, TreeNode[] nodes) {
        if (root == null) {
            return null;
        }

        for(TreeNode x : nodes) {
            if (x.val == root.val) {
                return root;
            }
        }

        TreeNode left = find(root.left, nodes);
        TreeNode right = find(root.right, nodes);
        if (left != null && right != null) {
            return root;
        }

        return left == null ? right : left;
    }
}

[剑指 Offer 33] 二叉搜索树的后续遍历树序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

示例 1：
输入: [1,6,3,2,5]
输出: false
示例 2：
输入: [1,3,2,6,5]
输出: true
提示：

数组长度 <= 1000

Related Topics

栈

树

二叉搜索树

递归

二叉树

单调栈

解法一：

从数组中分离开左右子树，检查其中元素和 rootVal之间的大小关系；然后递归

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        if (postorder.length < 2) {
            return true;
        }

        return traverse(postorder, 0, postorder.length-1);
    }

    private boolean traverse(int[] postorder, int left, int right) {
        if (left >= right) {
            return true;
        }
        // 因为是后序遍历，因此 root就是最后一个元素
        int rootVal = postorder[right];
		// 找到当前的右子树的序列开始位置(也就是右子树中的最小一个元素)
        int idx = left;
        while(idx < right) {
            if (rootVal < postorder[idx]) {
                break;
            }
            idx++;
        }
		// 校验以下后半段里面有没有元素比 rootVal小的，如果有就说明不符合 BST的规范
        for(int i = idx; i <= right; i++) {
            if (postorder[i] < rootVal) {
                return false;
            }
        }

        // 递归
        if (!traverse(postorder, left, idx - 1)) {
            return false;
        }

        if (!traverse(postorder, idx, right - 1)) {
            return false;
        }

        return true;
    }
}

[剑指 Offer Ⅱ 008] 和大于等于 target的最短子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：
输入：target = 4, nums = [1,4,4]
输出：1
示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0
提示：

1 <= target <= 109

1 <= nums.length <= 105

1 <= nums[i] <= 105

进阶：

如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

注意：本题与主站 209 题相同：https://leetcode-cn.com/problems/minimum-size-subarray-sum/

Related Topics

数组

二分查找

前缀和

滑动窗口

解法一：

滑动窗口

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        // HashMap<Integer, Integer> window = new HashMap<>();

        int left = 0, right = 0;
        int sum = 0, res = Integer.MAX_VALUE;
        while(right < nums.length) {
            int in = nums[right];
            // window.put(right, in);
            right++;
            sum += in;

            while(sum >= target && left < nums.length) {
                res = Math.min(res, right - left);
                int out = nums[left];
                sum -= out;
                // window.remove(left);
                left++;
            }
            
            
        }

        return res == Integer.MAX_VALUE ? 0 : res;
    }
}

困难难度

[4] 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2
示例 2：
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
提示：

nums1.length == m

nums2.length == n

0 <= m <= 1000

0 <= n <= 1000

1 <= m + n <= 2000

-106 <= nums1[i], nums2[i] <= 106

Related Topics

数组

二分查找

分治

解法一

使用二分查找，将求中位数视作求第 K个数，K= len/2，每次循环排除 k/2个数

假设我们要找第 7 小的数字，我们比较两个数组中的第 k/2 个数字，如果 k是奇数，就向下取整

两个数组中的数哪个小就将其排除，即该数组中的前 k/2个数字都不是第 k小数字

即下图中，3 < 4，则可排除 1 2 3这三个数，之后将数组 A和数组B(4 5 6 7 8 9 10) 重新进行比较

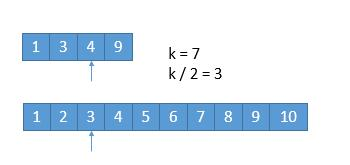
取一个更特殊的情况：

A[1], A[2], A[3] … A[k/2]
B[1], B[2], B[3] … B[k/2] …

如果此时 A[k/2] < B[k/2]那么所有 A数组中的内容都要被舍弃

由于我们已经排除掉了三个数字，则可知在真实的排序中（从大到小排）这三个数字肯定在前边，所以在新的数组中我们只需要找第7-3=4小的数字就行了，即第二次查的时候k = 4，k/2 = 2

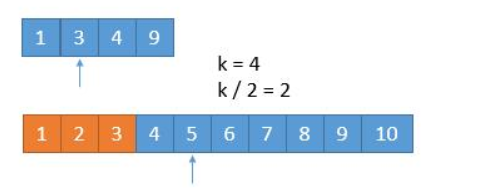
之后，由于 3 < 5 故排除 A数组中的 1 3

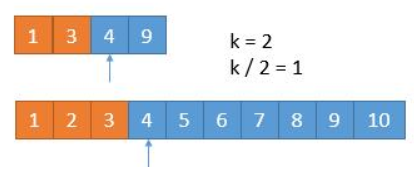
我们又排除掉了 2个数，所以现在找第 4 - 2 = 2个数就行，此时 k / 2 = 1，此时 A[k/2]和 B[k/2]相等，则无论剔除哪个都行只是每次都需要统一，这里选择剔除 B数组中的内容

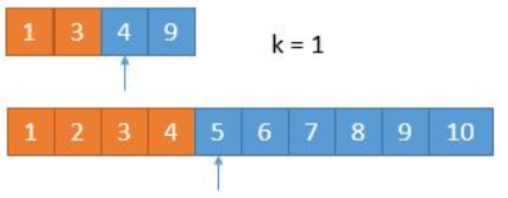
最后，k = 1，表示获取第 1 小的数，即获取最小的，只要判断 4 和 5哪个小就行了

注意：

我们每次都获取 k/2的数进行比较，而此时有可能会遇到数组长度小于 k/2的情况，此时 k/2 = 3，箭头无法向后指了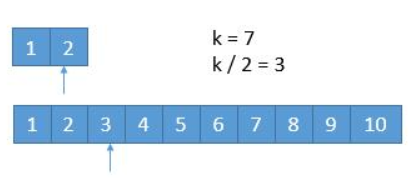
此时 A数组只能排除两个元素，k=5，又由于上边的数组已经空了，我们只需要返回下边数组的第 5个数字即可

所以，无论找奇数个还是偶数个，对我们的算法并没有影响，所以我们采用递归的思想，为了防止数组的长度小于 k / 2，所以每次比较 min(k/2, len(数组))对应的数字，把小的那个对应的数组的数字排除

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    int n = nums1.length;
    int m = nums2.length;
    int left = right = (n + m + 1) / 2;
    
    // 将奇数和偶数的情况合并，如果是奇数，也会求两次同样的 K
    return (getKth(nums1, 0, n-1, nums2, 0, m-1, left) + getKth(nums1, 0, n-1, nums2, 0, m-1, right)) / 2.0;
}

private double getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
    int len1 = end1 - start1 + 1;
    int len2 = end2 - start2 + 1;
    
    // 让 len1 < len2，这样就能保证如果有数组空了，一定是 len1
    if(len1 > len2) {
        return getKth(nums2, start2, end2, nums1, start1, end1, k);
    }
    
    // 有一个数组为空的情况
    if(len1 == 0) {
        return nums2[start2 + k - 1];
    }
    
    // 数组剩余长度不够的情况
    if(k == 1) {
        return Math.min(nums1[start1], nums2[start2]);
    }
    
    //  指针在两个数组中的定位
    int i = start1 + Math.min(len1, k / 2) - 1;
    int j = start2 + Math.min(len2, k / 2) - 1;
    
    // 判断剔除哪个数组中的元素
    if(nums1[i] > nums2[j]) {
        return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
    } else {
        return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
    }
}

[10] 正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s的，而不是部分字符串。

示例 1：
输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。
示例 2:
输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。
示例 3：
输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。
提示：

1 <= s.length <= 20

1 <= p.length <= 30

s 只包含从 a-z 的小写字母。

p 只包含从 a-z 的小写字母，以及字符 . 和 *。

保证每次出现字符 * 时，前面都匹配到有效的字符

Related Topics

递归

字符串

动态规划

解法一：

int[][] dp = new int[s.length+1][pattern+1]

dp[i][j]表示 pattern[0..j]匹配 s[0..i]的结果

另外针对 . 和 * 的问题，需要着重探讨

class Solution {
    public boolean isMatch(String s, String p) {
        int sLen = s.length();
        int pLen = p.length();

        int[][] dp = new int[sLen + 1][pLen + 1];

        //  base case
        dp[0][0] = 1;
        for (int i = 1; i <= pLen; i++) {
            if (p.charAt(i - 1) == '*') {
                dp[0][i] = dp[0][i - 2];
            }
        }

        // 进行 dp
        for (int i = 1; i <= sLen; i++) {
            for (int j = 1; j <= pLen; j++) {
                // 可以直接匹配
                if (s.charAt(i - 1) == p.charAt(j - 1)
                        || p.charAt(j - 1) == '.') {
                    dp[i][j] = dp[i - 1][j - 1];
                    // 通配符 *
                } else if (p.charAt(j - 1) == '*') {
                    // *前一个字符能够匹配
                    if (s.charAt(i - 1) == p.charAt(j - 2)
                            || p.charAt(j - 2) == '.') {
                        dp[i][j] = dp[i][j - 2] + dp[i - 1][j];
                    } else {
                        // *前一个字符不能匹配
                        dp[i][j] = dp[i][j - 2];
                    }
                }
            }
        }

        return dp[sLen][pLen] != 0;
    }
}

令附力扣的题解，更加简洁

class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length();
        int n = p.length();

        boolean[][] f = new boolean[m + 1][n + 1];
        // base case
        f[0][0] = true;
        
        for (int i = 0; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                // 如果是 *
                if (p.charAt(j - 1) == '*') {
                    // 先赋值也可以，这里不赋值，到 else中赋值也可以，反正如果匹配的话，会在 if中被覆盖
                    f[i][j] = f[i][j - 2];
                    if (matches(s, p, i, j - 1)) {
                        f[i][j] = f[i][j] || f[i - 1][j];
                    }
                    // 不是 *
                } else {
                    // 直接匹配
                    if (matches(s, p, i, j)) {
                        f[i][j] = f[i - 1][j - 1];
                    }
                }
            }
        }
        return f[m][n];
    }

    public boolean matches(String s, String p, int i, int j) {
        if (i == 0) {
            return false;
        }
        if (p.charAt(j - 1) == '.') {
            return true;
        }
        return s.charAt(i - 1) == p.charAt(j - 1);
    }
}

class Solution {
    public boolean isMatch(String s, String p) {
        boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
        dp[0][0] = true;
        for (int i = 1; i <= p.length(); i++) {
            // 匹配空字符串
            if (p.charAt(i - 1) == '*') {
                dp[0][i] = dp[0][i - 2];
            }
        }

        for(int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= p.length(); j++) {
                // 当前字符能够直接匹配
                if (s.charAt(i-1) == p.charAt(j-1) 
                    || p.charAt(j-1) == '.') {
                    dp[i][j] = dp[i-1][j-1];
                } else if (p.charAt(j-1) == '*') {
                    // * 的前一个字符能够匹配得上
                    if (s.charAt(i-1) == p.charAt(j-2) || p.charAt(j-2) == '.') {
                        dp[i][j] = dp[i-1][j] // *号前一个字符正好对应 s中的当前字符
                            || dp[i][j-2]; //  .一定能匹配上，那就直接看 .前面的字符字符就好
                    } else {
                        // * 的前一个字符匹配不上
                        dp[i][j] = dp[i][j-2];
                    }
                }
            }
        }

        
        return dp[s.length()][p.length()];
    }
}

[23] 合并 K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2：
输入：lists = []
输出：[]
示例 3：
输入：lists = [[]]
输出：[]
提示：

k == lists.length

0 <= k <= 10^4

0 <= lists[i].length <= 500

-10^4 <= lists[i][j] <= 10^4

lists[i] 按升序排列

lists[i].length 的总和不超过 10^4

Related Topics

链表

分治

堆（优先队列）

归并排序

解法一：

优先级队列

构造一个优先级队列，按照节点的值由小到大排列，队列中只存储每个链表中的一个节点；

每次将最小的节点出队，后入队该节点的下一个结点

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }   

        ListNode dummy = new ListNode(-1), cur = dummy;
        PriorityQueue<ListNode> queue = new PriorityQueue<>(lists.length, (o1, o2) -> o1.val - o2.val);

        for(ListNode head : lists) {
            // 注意这里也需要做非空判断
            if (head != null) {
                queue.add(head);
            }
        }

        // 同一时间，queue中只有 lists.length数量的 ListNode
        while(!queue.isEmpty()) {
            // 由于优先级队列的原因，这里弹出的一定是最小的 ListNode
            ListNode out = queue.poll();
            cur.next = out;
            cur = cur.next;
            if(out.next != null) {
                queue.add(out.next);
            }
        }

        return dummy.next;
    }
}

解法二：

顺序合并

把题目看作是多次进行 “两个链表的合并” 操作

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null) {
            return null;
        }

        ListNode res = null;
        for(int i = 0; i < lists.length; i++) {
          	// 直接进行【两个有序链表的合并】操作
            res = merge2Lists(res, lists[i]);
        }
        return res;
    }

    private ListNode merge2Lists(ListNode l1, ListNode l2) {
        ListNode p = l1, q = l2;
        ListNode dummy = new ListNode(), cur = dummy;

        while(p != null && q != null) {
            if (p.val >= q.val) {
                cur.next = q;
                q = q.next;
            } else {
                cur.next = p;
                p = p.next;
            }
            cur = cur.next;
        }

        cur.next = p == null ? q : p;

        return dummy.next;
    }
}

解法三：

分治

将每次将全量数据拆分成两半，最终还是依靠【两个升序链表的合并】实现

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        // 基本的校验
        if (lists == null || lists.length == 0) {
            return null;
        }
        return mergeKLists(lists, 0, lists.length - 1);
    }

    private ListNode mergeKLists(ListNode[] lists, int begin, int end) {
        
        if (begin > end) {
            return null;
        } else if (begin == end) {
            return lists[begin];
        }

        // 归并可以看作是大任务拆分成多个小任务
        int mid = begin + (end - begin) / 2;
        return merge2Lists(mergeKLists(lists, begin, mid), mergeKLists(lists, mid+1, end));
    }

    private ListNode merge2Lists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(-1), cur = dummy;
        ListNode p = l1, q = l2;

        while (p != null && q != null) {
            if (p.val >= q.val) {
                cur.next = q;
                q = q.next;
            } else {
                cur.next = p;
                p = p.next;
            }

            cur = cur.next;
        }

        cur.next = p == null ? q : p;
        return dummy.next;
    }
}

[25] K个一组翻转链表

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。

k 是一个正整数，它的值小于或等于链表的长度。

如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

进阶：

你可以设计一个只使用常数额外空间的算法来解决此问题吗？
你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

示例 3：
输入：head = [1,2,3,4,5], k = 1
输出：[1,2,3,4,5]

示例 4：
输入：head = [1], k = 1
输出：[1]

提示：
列表中节点的数量在范围 sz 内
1 <= sz <= 5000
0 <= Node.val <= 1000
1 <= k <= sz

解法一：

递归

因为 k个一组反转 n个节点中的链表，和针对 n-k个节点中反转，n-2k, n-3k…中是一样的

那么就可以设置退出递归的条件：

当剩下的节点个数 < k，那么就不反转

其余的时候，每 k个进行递归

class Solution {
      public ListNode reverseKGroup(ListNode head, int k) {
        if (k == 1 || head == null) {
            return head;
        }

        ListNode a, b;
        a = b = head;

        // 将 b定位到从 head开始的 k个位置之后
        for (int i = 0; i < k; i++) {
            // 如果剩余节点个数不够了，就直接返回
            if (b == null)  {
                return head;
            }
            b = b.next;
        }

        // 反转前 k个元素
        ListNode newHead = reverse(a, b);
        // 将递归反转后的链表拼接起来
        a.next = reverseKGroup(b, k);
        // 排序部分的头
        return newHead;
    }

    private ListNode reverse(ListNode a, ListNode b) {
        ListNode cur, pre, nex;
        cur = nex = a;
        pre = null;
        while (cur != b) {
            nex = cur.next;
            // 当前节点指向前面一个结点
            cur.next = pre;

            // 跟新指针的位置
            pre = cur;
            cur = nex;
        }

        // 返回反转后的首元结点
        return pre;
    }
}

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || k == 1) {
            return head;
        }

        ListNode scout = head;
        for(int i = 0; i < k; i++) {
            if (scout == null) {
                return head;
            }
            scout = scout.next;
        }

        ListNode first = reverse(head, k);
        head.next  = reverseKGroup(scout, k);
        return first;
    }

    private ListNode reverse(ListNode head, int k) {
        if (k == 1) {
            return head;
        }

        ListNode tail = traverse(head.next, k-1);
        head.next.next = head;
        head.next = null;

        return tail;
    }
}

解法二：

借助栈的先进后出

在链表中，每 k个元素进一次栈，然后统一出栈，依据出栈的顺序链接

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (k == 1) {
            return head;
        }

        // p和 rh其实都是头节点，p.next就是首元结点
        ListNode p = new ListNode();
        ListNode q = head, rh = p;
        LinkedList<ListNode> list = new LinkedList<ListNode>();
        while (q != null) {
            head = q;
            // 扔到栈里面
            for (int i = 0; i < k && q != null; i++) {
                list.addLast(q);
                q = q.next;
            }
            // 如果栈内元素的数量不是 k个的话，就不反转，直接连上，并且这个时候它肯定是在最后了的
            if (list.size() != k) {
                p.next = head;
                // 否则逐个反转
            } else {
                for (int i = 0; i < k; i++) {
                    p.next = list.pollLast();
                    p = p.next;
                }
                p.next = null;
            }
        }
        return rh.next;
    }
}

[42] 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 
示例 2：
输入：height = [4,2,0,3,2,5]
输出：9
提示：

n == height.length

1 <= n <= 2 * 104

0 <= height[i] <= 105

Related Topics

栈

数组

双指针

动态规划

单调栈

解法一：

动态规划

class Solution {
    public int trap(int[] height) {
        if (height.length == 0) {
            return 0;
        }

        int res = 0;
        // 左右侧当 i  的最高点
        int[] l_max = new int[height.length];
        int[] r_max = new int[height.length];
        // 初始化
        l_max[0] = height[0];
        r_max[height.length - 1] = height[height.length - 1];

        for(int i = 1; i < height.length; i++) {
            l_max[i] = Math.max(height[i], l_max[i-1]);
        }
        for(int i = height.length - 2; i >= 0; i--) {
            r_max[i] = Math.max(height[i], r_max[i + 1]);
        }
		
        // 第 i 处的容积就是左右侧最高点中的最低点和 height[i]的差值
        for(int i = 1; i < height.length - 1; i++) {
            res += Math.min(l_max[i], r_max[i]) - height[i];
        }
        return res;
    }
}

解法二：

双指针

class Solution {
    public int trap(int[] height) {
        int res = 0;
        int left = 0, right = height.length - 1;
        int leftMax = 0, rightMax = 0;

        while(left < right) {
            leftMax = Math.max(leftMax, height[left]);
            rightMax = Math.max(rightMax, height[right]);

            if (height[left] < height[right]) {
                res += leftMax - height[left++];
            } else {
                res += rightMax - height[right--];
            }
        }

        return res;
    }
}

[51] N皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。
示例 2：
输入：n = 1
输出：[["Q"]]
提示：

1 <= n <= 9

皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

Related Topics

数组

回溯

解法一：

回溯

class Solution {

    List<List<String>> res = new ArrayList<>();
    List<String> path = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        char[][] arr = new char[n][n];
        for(char[] x : arr) {
            Arrays.fill(x, '.');
        }

        traverse(arr, n, 0);
        return res;
    }

    private void traverse(char[][] arr, int n, int row) {
        if (row == n) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 使用 row来控制递归，使用 col来进行循环
        for(int col = 0; col < n; col++) {
            if(!isValid(arr, row, col)) {
                continue;
            }

            // 等于说，一次回溯需要修改两个值
            arr[row][col]  = 'Q';
            path.add(parseStr(arr, row));
            
            traverse(arr, n, row + 1);
            
            path.remove(path.size() - 1);
            arr[row][col] = '.';
        }
    }

    private String parseStr(char[][] arr, int row) {
        StringBuffer sb = new StringBuffer();
        for(char x : arr[row]) {
            sb.append(x);
        }
        return sb.toString();
    }

    // 判断能不能放在当前的位置
    private boolean isValid(char[][] arr, int row, int col) {
        for(int i = 0; i < row; i++) {
            if (arr[i][col] == 'Q') {
                return false;
            }
        }

        for(int i = row - 1, j = col + 1; i >= 0 && j < arr.length; i--, j++) {
             if (arr[i][j] == 'Q') {
                return false;
            }
        }

        for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
             if (arr[i][j] == 'Q') {
                return false;
            }
        }

        return true;
    }
}

[72] 编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

Related Topics

字符串

动态规划

解法一：

记牢吧

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length(), len2 = word2.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        // 针对 一个是串，另一个是空值的情况；编辑距离就是串长
        for (int i = 1; i <= len1; i++) {
            dp[i][0] = i;
        }
        for (int i = 1; i <= len2; i++) {
            dp[0][i] = i;
        }


        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                // 如果当前两个值相等，那么当前值，就是斜对角线的上一个值
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    // 否则计算三种情况（加、减、替换）的最小值，记得加一
                    dp[i][j] = min(dp[i][j - 1] + 1,
                            dp[i - 1][j] + 1,
                            dp[i - 1][j - 1] + 1);
                }
            }
        }

        return dp[len1][len2];
    }

    private int min(int a, int b, int c) {
        return Math.min(a, Math.min(b, c));
    }
}

[76] 覆盖最小子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
示例 2：
输入：s = "a", t = "a"
输出："a"
示例 3:
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。
提示：

1 <= s.length, t.length <= 105

s 和 t 由英文字母组成

进阶：你能设计一个在 o(n) 时间内解决此问题的算法吗？

Related Topics

哈希表

字符串

滑动窗口

解法一：

滑动窗口

构建两个哈希表，分别存储需要的某些字符的数量，和当前窗口中某个字符的数量，键与值分别是 Character 和 Integer 代表某一字符和它出现的次数

具体解析看 day7: 滑动窗口技巧

class Solution {
    public String minWindow(String s, String t) {

        HashMap<Character, Integer> need = new HashMap<>();
        HashMap<Character, Integer> window = new HashMap<>();

        for (int i = 0; i < t.length(); i++) {
            char key = t.charAt(i);
            need.put(key, need.getOrDefault(key, 0) + 1);
        }

        // 前闭后开，初始状态下没有包涵元素
        int left = 0, right = 0;
        // valid表示已满足条件的字符
        int valid = 0;

        // 记录最小覆盖子串的其实索引及长度
        int start = 0, len = Integer.MAX_VALUE;

        while (right < s.length()) {

            // c是将进入窗口的字符
            char c = s.charAt(right);

            // 右移窗口
            right++;

            // 进行窗口内数据的一系列更新
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                if (window.get(c).equals(need.get(c))) {
                    valid++;
                }
            }

            // 判断左窗口是否要收紧
            while (valid == need.size()) {

                // 在这里更新最小覆盖子串
                if ((right - left) < len) {
                    start = left;
                    len = right - left;
                }

                // d是将移出窗口的字符
                char d = s.charAt(left);

                // 左移窗口
                left++;
                if (need.containsKey(d)) {
                    if (window.get(d).equals(need.get(d))) {
                        valid--;
                    }
                    window.put(d, window.getOrDefault(d, 0) - 1);
                }
            }

        }

        return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
    }
}

[84] 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10
示例 2：
输入： heights = [2,4]
输出： 4
提示：

1 <= heights.length <=105

0 <= heights[i] <= 104

Related Topics

栈

数组

单调栈

解法一：

类似接雨水，记录从左到右，从右到左的比当前位置小的值

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] left = new int[heights.length];
        int[] right = new int[heights.length];

        // 注意这里赋值为 -1
        left[0] = -1;
        for(int i = 1; i < heights.length; i++) {
            int idx = i - 1;
            while(idx >= 0 && heights[idx] >= heights[i]) {
                // 此时可以明确的是，idx 在 i 的 左边，且 idx 更高
                // 那么可以直接获取 left[idx]，其中就记录了比 idx 矮的位置，可能也会比 i 矮
                // 这样相比于 i-- 能得到速度的提升
                idx = left[idx];
            }
            left[i] = idx; // 注意记录的是位置，不是值
        }

        // 注意这里赋值为 heights.length
        right[heights.length - 1] = heights.length;
        for(int i = heights.length - 2; i >= 0; i--) {
            int idx = i + 1;
            while(idx <= heights.length - 1 && heights[idx] >= heights[i]) {
                idx = right[idx];
            }
            right[i] = idx;
        }


        int max = 0;
        for(int i = 0; i < heights.length; i++) {
            //        对比 max   和     高度 * 宽度，注意宽度需要 - 1
            max = Math.max(max, heights[i] * (right[i] - left[i] - 1));
        }
        return max;
    }
}

或者使用【单调栈】来获取上一个比自己小的下标

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] left = new int[heights.length];
        int[] right = new int[heights.length];
        Stack<Integer> stack = new Stack<>();

        for(int i = 0; i < heights.length; i++) {
            while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
                stack.pop();
            }
            left[i] = stack.isEmpty() ? -1 : stack.peek();
            stack.push(i);
        }

        stack.clear();
        for(int i = heights.length - 1; i >= 0; i--) {
            while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
                stack.pop();
            }
            right[i] = stack.isEmpty() ? heights.length : stack.peek();
            stack.push(i);
        }


        int max = 0;
        for(int i = 0; i < heights.length; i++) {
            //        对比 max   和     高度 * 宽度
            max = Math.max(max, heights[i] * (right[i] - left[i] - 1));
        }
        return max;
    }
}

[85] 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。
示例 2：
输入：matrix = []
输出：0
示例 3：
输入：matrix = [["0"]]
输出：0
示例 4：
输入：matrix = [["1"]]
输出：1
示例 5：
输入：matrix = [["0","0"]]
输出：0
提示：

rows == matrix.length

cols == matrix[0].length

1 <= row, cols <= 200

matrix[i][j] 为 '0' 或 '1'

Related Topics

栈

数组

动态规划

矩阵

单调栈

解法一：

逐行来看，就可以视作为 84题的柱状图中最大矩形

class Solution {
    public int maximalRectangle(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }

        int row = matrix.length, col = matrix[0].length;
        int[] heights = new int[col];
        int max = 0;
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                // 构造 heights数组
                if (matrix[i][j] == '1') {
                    heights[j] += 1;
                } else {
                    heights[j] = 0;
                }
            }
            // 调用 84题的题解来求
            max = Math.max(max, findLargest(heights));
        }

        return max;
    }


    private int findLargest(int[] heights) {
        int[] left = new int[heights.length];
        int[] right = new int[heights.length];
        
        left[0] = -1;
        for(int i = 1; i < heights.length; i++) {
            int idx = i - 1;
            while(idx >= 0 && heights[idx] >= heights[i]) {
                idx = left[idx];
            }
            left[i] = idx;
        }

        right[heights.length - 1] = heights.length;
        for(int i = heights.length - 2; i >= 0; i--) {
            int idx = i + 1;
            while(idx < heights.length && heights[idx] >= heights[i]) {
                idx = right[idx];
            }
            right[i] = idx;
        }

        int max = 0;
        for(int i = 0; i < heights.length; i++) {
            max = Math.max(max, heights[i] * (right[i] - left[i] - 1));
        }

        return max;
    }
}

[123] 买卖股票的最佳时机Ⅲ

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
  随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。   
  注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。   
  因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3：

输入：prices = [7,6,4,3,1] 
输出：0 
解释：在这个情况下, 没有交易完成, 所以最大利润为 0。

示例 4：

输入：prices = [1]
输出：0

提示：

1 <= prices.length <= 105
0 <= prices[i] <= 105

Related Topics

数组

动态规划

解法一：

神仙解法

class Solution {
    public int maxProfit(int[] prices) {
        int[] buy = new int[3];
        int[] sell = new int[3];
        for(int i = 0; i <= 2; i++) {
            buy[i] = Integer.MIN_VALUE;
            sell[i] = 0;
        }

        for(int x : prices) {
            for(int i = 1; i <= 2; i++) {
                buy[i] = Math.max(buy[i], sell[i-1] - x);
                sell[i] = Math.max(sell[i], buy[i] + x);
            }
        }

        return sell[2];
    }
}

[124] 二叉树中的最大路径和

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42
提示：

树中节点数目范围是 [1, 3 * 104]

-1000 <= Node.val <= 1000

Related Topics

树

深度优先搜索

动态规划

二叉树

解法一：

就普通的递归，看清楚题目，这条路径是不能分叉的；

也就是说对于中间的某一个节点来说，只有两种选择：

选择左子树+自己+右子树，组成最大值；
选择自己+左右最大子树，奉献给父节点，组成最大值；

class Solution {
    int res = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        traverse(root);
        return res;
    }

    private int traverse(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 计算左子树中的最值
        int left = Math.max(0, traverse(root.left));
        // 计算右子树中的最值
        int right = Math.max(0, traverse(root.right));
        
        // 此时更新 res，因为当前节点可能不像上传递，那么就以 root作为桥梁，联通左右子树
        res = Math.max(res, left + right + root.val);

        // 注意题干【沿父节点-子节点连接】也就是说如果当前节点要向上传递值，那么随带着的最多只能传递左右子树中的一个值！！！
        // 因为需要选取左右子树值的更大者搭配当前 root.val 向上传递
        return Math.max(left, right) + root.val;
    }
}

[188] 买卖股票的最佳实际Ⅳ

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：

输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
  随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

提示：

0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000

Related Topics

数组

动态规划

解法一：

和上题一样，忽然想通了

其实 buy 和 sell，就算数组空间压缩后的值

class Solution {
    public int maxProfit(int k, int[] prices) {
        k = Math.min(k, prices.length);
        int[] buy = new int[k+1];
        int[] sell = new int[k+1];

        for(int i = 0; i <= k; i++) {
            buy[i] = Integer.MIN_VALUE;
            sell[i] = 0;
        }

        for(int x : prices) {
            for(int i = 1; i <= k; i++) {
                buy[i] = Math.max(buy[i], sell[i-1] - x);
                sell[i] = Math.max(sell[i], buy[i] + x);
            }
        }

        return sell[k];
    }
}

[239] 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
1 [3  -1  -3] 5  3  6  7       3
1  3 [-1  -3  5] 3  6  7       5
1  3  -1 [-3  5  3] 6  7       5
1  3  -1  -3 [5  3  6] 7       6
1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

示例 3：

输入：nums = [1,-1], k = 1
输出：[1,-1]

示例 4：

输入：nums = [9,11], k = 2
输出：[11]

示例 5：

输入：nums = [4,-2], k = 2
输出：[4]

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length

Related Topics

队列

数组

滑动窗口

单调队列

堆（优先队列）

解法一：

单调队列

使用单调队列存储窗口中的数

详解参看 day10: 单调队列和单调栈

class Solution {
    // 声明集合作为窗口
    LinkedList<Integer> window = new LinkedList<>();

    public int[] maxSlidingWindow(int[] nums, int k) {
        // 声明结果数组
        int[] res = new int[nums.length - k + 1];
        int j = 0;

        // 遍历数组
        for (int i = 0; i < nums.length; i++) {

            // 先把前 k-1个数推进窗口
            if (i < k - 1) {
                push(nums[i]);

            } else {
                push(nums[i]);
                // 记录当前窗口中最大的数
                res[j++] = max();
                // 删除窗口中最左侧的数
                pop(nums[i - k + 1]);
            }

        }
        return res;
    }

    /**
     * 将元素 n压入窗口中，如果倒着遍历窗口，有比 n小的元素，就移除它们，这样可以保证集合中最左的那个是最大的数
     * 如果进来的顺序是 1 2 3 4的话，那么在集合中就只会保存一个 4
     * 但是如果进来的顺序是 4 3 2 1 的话，就都会保存
     * 这样的好处是：使得集合内的数尽可能有序（从大到小排列）
     *
     * @param n
     */
    private void push(int n) {
        while (!window.isEmpty() && window.getLast() < n) {
            window.pollLast();
        }
        window.addLast(n);
    }

    /**
     * 返回最大的数，即集合中最左侧的数
     *
     * @return
     */
    private int max() {
        return window.getFirst();
    }

    /**
     * 按照值移除数
     *
     * @param n
     */
    private void pop(int n) {
        if (n == window.getFirst()) {
            window.pollFirst();
        }
    }
}

第二次手写

别用 queue的 api

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] res = new int[nums.length - k  + 1];
        // 单调队列
        LinkedList<Integer> queue = new LinkedList<>();

        for(int i = 0; i < nums.length; i++) {
            // 保证当前队列中的其它比 nums[i]小的元素都没了
            while(!queue.isEmpty() && queue.getFirst() < nums[i]) {
                queue.removeFirst();
            }
            queue.addFirst(nums[i]);

            // 遍历了 k个之后，就需要给 res赋值了
            if (i >= k - 1) {
                res[i - k + 1] = queue.getLast();
                // 这个 nums[i - k + 1]很重要！！
                if (nums[i - k + 1] == queue.getLast()) {
                    queue.removeLast();
                }
            }
        }

        return res;
    }
}

[295] 数据流的中位数

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

示例：
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3) 
findMedian() -> 2
进阶:

如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？

如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

Related Topics

设计

双指针

数据流

排序

堆（优先队列）

解法一：

优先级队列

class MedianFinder {

    PriorityQueue<Integer> queueMin;
    PriorityQueue<Integer> queueMax;

    public MedianFinder() {
        // 大顶堆
        queueMin = new PriorityQueue<>((o1, o2)-> o2-o1);
        // 小顶堆
        queueMax = new PriorityQueue<>((o1, o2)-> o1-o2);
    }
    
    public void addNum(int num) {
        // if (queueMin.isEmpty() || num <= queueMin.peek()) {
        //     queueMin.offer(num);
		// 这里之所以要 + 1是因为，如果不加一，那么第一个值就一定会被扔给 max
        // 如果第二个值比第一个值大，那么大的那个值就会到 min中了，就出问题了
        //     if (queueMax.size() + 1 < queueMin.size()) {
        //         queueMax.offer(queueMin.poll());
        //     }
        // } else {
        //     queueMax.offer(num);
        //     if (queueMin.size() < queueMax.size()) {
        //         queueMin.offer(queueMax.poll());
        //     }
        // }
        
        // 上下两种都可以

        if (queueMin.size() >= queueMax.size()) {
            queueMin.offer(num);
            queueMax.offer(queueMin.poll());
        } else {
            queueMax.offer(num);
            queueMin.offer(queueMax.poll());
        }
    }
    
    public double findMedian() {
        if (queueMin.size() > queueMax.size()) {
            return queueMin.peek();
        } else if (queueMax.size() > queueMin.size()) {
            return queueMax.peek();
        }

        return (queueMin.peek() + queueMax.peek()) / 2.0;
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

[297] 二叉树的序列化和反序列化

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1：
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]
示例 2：
输入：root = []
输出：[]
示例 3：
输入：root = [1]
输出：[1]
示例 4：
输入：root = [1,2]
输出：[1,2]
提示：

树中结点数在范围 [0, 104] 内

-1000 <= Node.val <= 1000

Related Topics

树

深度优先搜索

广度优先搜索

设计

字符串

二叉树

解法一：

层序

public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if (root == null) {
            return "#";
        }

        Queue<TreeNode> queue = new LinkedList<>();
        List<String> res = new ArrayList<>();
        queue.offer(root);
        while (queue.size() != 0) {

            TreeNode node = queue.poll();
            if (node == null) {
                res.add("#");
            } else {
                res.add(String.valueOf(node.val));
                // 不管有没有左右孩子，都放入队列中
                queue.offer(node.left);
                queue.offer(node.right);
            }
        }

        String join = String.join(",", res);
        return join;
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] split = data.split(",");
        if (split[0].equals("#")) {
            return null;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        TreeNode r = new TreeNode(Integer.parseInt(split[0]));
        queue.offer(r);
        // 怎么获取串的，就怎么构建二叉树
        for (int i = 1; i < split.length; ) {
            
            TreeNode root = queue.poll();
            
            String lNode = split[i++];
            if (!lNode.equals("#")) {
                root.left = new TreeNode(Integer.parseInt(lNode));
                queue.offer(root.left);
            } else {
                root.left = null;
            }

            String rNode = split[i++];
            if (!rNode.equals("#")) {
                root.right = new TreeNode(Integer.parseInt(rNode));
                queue.offer(root.right);
            } else {
                root.right = null;
            }
        }

        return r;
    }

}

解法二：

先序遍历

public class Codec {
    // 初次遍历的结果
    List<String> res = new ArrayList<>();
    public String serialize(TreeNode root) {
        encode(root);
        return String.join(",", res);
    }

    private void encode(TreeNode root) {

        if (root == null) {
            res.add("#");
            return;
        }
        res.add(String.valueOf(root.val));
        encode(root.left);
        encode(root.right);
    }

    // 生成二叉树时的数据下标
    int idx = -1;
    public TreeNode deserialize(String data) {
        String[] split = data.split(",");
        TreeNode root = decode(split);
        return root;
    }

    private TreeNode decode(String[] split) {
        idx++;
        if (idx >= split.length) {
            return null;
        }

        if (split[idx].equals("#")) {
            return null;
        }

        int val = Integer.parseInt(split[idx]);
        TreeNode root = new TreeNode(val);

        root.left = decode(split);
        root.right = decode(split);
        return root;
    }
}

解法三：

后序遍历

public class Codec {
    List<String> res = new ArrayList<>();

    public String serialize(TreeNode root) {
        encode(root);
        return String.join(",", res);
    }

    private void encode(TreeNode root) {
        if (root == null) {
            res.add("#");
            return;
        }
        encode(root.left);
        encode(root.right);
        res.add(String.valueOf(root.val));
    }

    int idx;
    public TreeNode deserialize(String data) {
        String[] split = data.split(",");
        idx = split.length;
        return decode(split);
    }

    private TreeNode decode(String[] split) {
        idx--;
        if (idx == 0) {
            return null;
        }

        if (split[idx].equals("#")) {
            return null;
        }

        TreeNode root = new TreeNode(Integer.parseInt(split[idx]));
        root.right = decode(split);
        root.left = decode(split);
        return root;
    }
}

[301] 删除无效的括号

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按 任意顺序 返回。

示例 1：
输入：s = "()())()"
输出：["(())()","()()()"]
示例 2：
输入：s = "(a)())()"
输出：["(a())()","(a)()()"]
示例 3：
输入：s = ")("
输出：[""]
提示：

1 <= s.length <= 25

s 由小写英文字母以及括号 '(' 和 ')' 组成

s 中至多含 20 个括号

Related Topics

广度优先搜索

字符串

回溯

解法一：

回溯

class Solution {
    List<String> res = new ArrayList<>();

    /* 
    总体流程：
    1. 先计算需要移除的左右括号数量
    2. 回溯进行移除，移除时做好剪枝操作
    */

    public List<String> removeInvalidParentheses(String s) {
        int lremove = 0;
        int rremove = 0;
        // 记录需要修改的左右括号的数量
        for(char x : s.toCharArray()) {
            if (x == '(') {
                lremove++;
            } else if (x == ')') {
                if (lremove == 0) {
                    rremove++;
                } else {
                    lremove--;
                }
            }
        }

        backtrack(s, 0, lremove, rremove);
        return res;
    }

    private void backtrack(String s, int start, int lremove, int rremove) {
        if (lremove == 0 && rremove == 0) {
            // 判断是否符合要求
            if (isValid(s)) {
                res.add(s);
            }
            return;
        }

        for(int i = start; i < s.length(); i++) {
            // 去重，(((()，保证 ( 只需要计算一次就行了
            if (i != start && s.charAt(i) == s.charAt(i - 1)) {
                continue;
            }
            // 剩余的字符数量不够删了，直接返回
            if (lremove + rremove > s.length() - i) {
                return;
            }
            // 去除当前左括号，其实删了也不一定保证得到的结果符合要求，所以需要在向 res 添加结果值的时候做好校验
            if (lremove > 0 && s.charAt(i) == '(') {
                backtrack(s.substring(0, i) + s.substring(i + 1), i, lremove - 1, rremove);
            }
            // 去除当前右括号
            if (rremove > 0 && s.charAt(i) == ')') {
                backtrack(s.substring(0, i) + s.substring(i + 1), i, lremove, rremove - 1);
            }
        }
    }

    // 校验括号是否匹配
    private boolean isValid(String s) {
        int cnt = 0;
        for(char x : s.toCharArray()) {
            if (x == '(') {
                cnt++;
            } else if (x == ')') {
                cnt--;
                if (cnt < 0) {
                    return false;
                }
            }
        }

        return cnt == 0;
    }
}

[312] 戳气球

有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。

求所能获得硬币的最大数量。

示例 1：
输入：nums = [3,1,5,8]
输出：167
解释：
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins =  3*1*5    +   3*5*8   +  1*3*8  + 1*8*1 = 167
示例 2：
输入：nums = [1,5]
输出：10
提示：

n == nums.length

1 <= n <= 300

0 <= nums[i] <= 100

Related Topics

数组

动态规划

解法一：

三层循环动态规划，注意最后戳破气球的位置

class Solution {
    public int maxCoins(int[] nums) {
        int n = nums.length;
        // 额外使用 points，左右都留出一位之后，就不用担心边界情况了
        int[] points = new int[n + 2];
        points[0] = points[n + 1] = 1;
        for(int i = 1; i <= n; i++) {
            points[i] = nums[i - 1];
        }

        // dp[i][j] 表示在开区间 (i, j)内戳破所有气球后，能获得的最大数
        int[][] dp = new int[n + 2][n + 2];
        /*
                x x x x x
                  x x x x
                    x x x
                      x x
                        x
         */
         // 从下往上
        for (int i = n; i >= 0; i--) {
            // 从左往右
            for (int j = i + 1; j < n + 2; j++) {
                // 最后戳破的气球位置 k
                // 则 dp[i][j] = dp[i][k] + dp[k][j] + 关于 i, k, j 三个位置的 points乘积
                for(int k = i + 1; k < j; k++) {
                    dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + points[i] * points[j] * points[k]);
                }
            }
        }
		// 注意次数 0 和 n+1 都是虚拟结点
        return dp[0][n + 1];
    }
}

[315] 计算右侧小于当前元素的个数

给你`一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例 1：
输入：nums = [5,2,6,1]
输出：[2,1,1,0] 
解释：
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2：
输入：nums = [-1]
输出：[0]
示例 3：
输入：nums = [-1,-1]
输出：[0,0]
提示：

1 <= nums.length <= 105

-104 <= nums[i] <= 104

Related Topics

树状数组

线段树

数组

二分查找

分治

有序集合

归并排序

解法一：

归并

class Solution {
    private Pair[] tmp;
    private int[] count;

    public List<Integer> countSmaller(int[] nums) {
        tmp = new Pair[nums.length];
        count = new int[nums.length];
        Pair[] arr = new Pair[nums.length];
        for(int i = 0; i < nums.length; i++) {
            arr[i] = new Pair(nums[i], i);
        }

        sort(arr, 0, arr.length - 1);
        List<Integer> res = new ArrayList<>();
        for(int x : count) {
            res.add(x);
        }
        return res;
    }

    private void sort(Pair[] arr, int left, int right) {
        if (left >= right) {
            return;
        }

        int mid = left + (right - left) / 2;
        sort(arr, left, mid);
        sort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }

    private void merge(Pair[] arr, int left, int mid, int right) {
        for (int i = left; i <= right; i++) {
            tmp[i] = arr[i];
        }

        int p = left, q = mid + 1;
        for(int i = left; i <= right; i++) {
            if (p >= mid + 1) {
                arr[i] = tmp[q++];
            } else if (q >= right + 1) {
                arr[i] = tmp[p++];
                // 核心步骤
                count[arr[i].idx] += q - mid - 1;
            } else if (tmp[p].val <= tmp[q].val) {
                arr[i] = tmp[p++];
                // 核心步骤
                count[arr[i].idx] += q - mid - 1;
            } else {
                arr[i] = tmp[q++];
            }
        }
    }


    private class Pair {
        int val, idx;
        Pair(int val, int idx) {
            this.val = val;
            this.idx = idx;
        }
    }
}

[354] 俄罗斯套娃信封问题

给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi] ，表示第 i 个信封的宽度和高度。

当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

注意：不允许旋转信封。

示例 1：
输入：envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
示例 2：
输入：envelopes = [[1,1],[1,1],[1,1]]
输出：1
提示：

1 <= envelopes.length <= 105

envelopes[i].length == 2

1 <= wi, hi <= 105

Related Topics

数组

二分查找

动态规划

排序

解法一：

先对 envelops[][]数组进行排序，然后类似最长子序列问题

但是使用 dp需要 O(N²)的时间复杂度，现在力扣加了一个很长的测试用例，这么写就会超时

。。。

解法二：

二分查找

不太懂，面试遇上也只写 DP那种

class Solution {
    public int maxEnvelopes(int[][] envelopes) {

        int len = envelopes.length;
        // 按宽度升序排列，如果宽度一样，则按高度降序排列
        Arrays.sort(envelopes, (a, b) -> {
            return a[0] == b[0] ? b[1] - a[1] : a[0] - b[0];
        });


        int[] dp = new int[len];

        /*Arrays.fill(dp, 1);
        int max = 1;
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < i; j++) {
                if (envelopes[i][1] > envelopes[j][1]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            max = Math.max(dp[i], max);
        }

        return max;*/

        int piles = 0;
        for (int i = 0; i < len; i++) {
            int target = envelopes[i][1];
            int left = 0, right = piles;
            while (left < right) {
                int mid = left + (right - left) / 2;
                if (dp[mid] >= target) {
                    right = mid;
                } else {
                    left = mid + 1;
                }
            }

            if (left == piles) {
                piles++;
            }

            dp[left] = target;
        }

        return piles;
    }
}

[410] 分割数组的最大值

给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

设计一个算法使得这 m 个子数组各自和的最大值最小。

示例 1：
输入：nums = [7,2,5,10,8], m = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。 
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。
示例 2：
输入：nums = [1,2,3,4,5], m = 2
输出：9
示例 3：
输入：nums = [1,4,4], m = 3
输出：4
提示：

1 <= nums.length <= 1000

0 <= nums[i] <= 106

1 <= m <= min(50, nums.length)

Related Topics

贪心

数组

二分查找

动态规划

解法一：

二分查找

class Solution {
    public int splitArray(int[] nums, int m) {
        int low = 0, high = 0;
        // 最小值为数组中单个最大的值，最大值是数组中所有数的和
        for (int i = 0; i < nums.length; i++) {
            low = Math.max(low, nums[i]);
            high += nums[i];
        }

        // 通过依照某一容量切分数组后得到的数组个数，进行二分查找
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (split(nums, mid) == m) {
                high = mid - 1;
            } else if (split(nums, mid) < m) {
                high = mid - 1;
            } else if (split(nums, mid) > m) {
                low = mid + 1;
            }
        }

        return low;

    }

    private int split(int[] nums, int max) {
        int cnt = 1;
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            // 如果存不下了，说明要切分了，当前元素就是下一个子数组的第一个元素
            if (sum + nums[i] > max) {
                cnt++;
                sum = nums[i];
            } else {
                sum += nums[i];
            }
        }
        return cnt;
    }
}

第二次手写

class Solution {
    public int splitArray(int[] nums, int m) {
        int left = 0, right  = 0;
        for(int x : nums) {
            left = Math.max(left, x);
            right += x;
        }

        while(left < right) {
            int mid = left + (right - left) / 2;
            if (f(mid, nums) == m) {
                right = mid;
            } else if (f(mid, nums) < m) {
                right = mid;
            } else if (f(mid, nums) > m) {
                left = mid + 1;
            }
        }

        return left;
    }

    private int f(int max, int[] nums) {
        int cnt = 0;
        int sum = 0;
        for(int x : nums) {
            if (sum + x > max) {
                cnt++;
                sum = 0;
            }
            sum += x;
        }
        cnt++;

        return cnt;
    }
}

[460] LFU缓存

请你为最不经常使用（LFU）缓存算法设计并实现数据结构。

实现 LFUCache 类：

LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
int get(int key) - 如果键存在于缓存中，则获取键的值，否则返回 -1。
void put(int key, int value) - 如果键已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量时，则应该在插入新项之前，使最不经常使用的项无效。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最近最久未使用 的键。

注意「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。

为了确定最不常使用的键，可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。

当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

示例：

输入：
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出：
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]

解释：
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序（最左边的元素是最近的）
LFUCache lFUCache = new LFUCache(2);
lFUCache.put(1, 1);   // cache=[1,_], cnt(1)=1
lFUCache.put(2, 2);   // cache=[2,1], cnt(2)=1, cnt(1)=1
lFUCache.get(1);      // 返回 1
                   // cache=[1,2], cnt(2)=1, cnt(1)=2
lFUCache.put(3, 3);   // 去除键 2 ，因为 cnt(2)=1 ，使用计数最小
                   // cache=[3,1], cnt(3)=1, cnt(1)=2
lFUCache.get(2);      // 返回 -1（未找到）
lFUCache.get(3);      // 返回 3
                   // cache=[3,1], cnt(3)=2, cnt(1)=2
lFUCache.put(4, 4);   // 去除键 1 ，1 和 3 的 cnt 相同，但 1 最久未使用
                   // cache=[4,3], cnt(4)=1, cnt(3)=2
lFUCache.get(1);      // 返回 -1（未找到）
lFUCache.get(3);      // 返回 3
                   // cache=[3,4], cnt(4)=1, cnt(3)=3
lFUCache.get(4);      // 返回 4
                   // cache=[3,4], cnt(4)=2, cnt(3)=3

提示：

0 <= capacity, key, value <= 104
最多调用 105 次 get 和 put 方法

进阶：你可以为这两种操作设计时间复杂度为 O(1) 的实现吗？

Related Topics

设计

哈希表

链表

双向链表

解法一：

使用多个哈希表存储键值对、键和频率、频率和多个键

详见 day16: LFU算法

class LFUCache {

    // 缓存容量
    int capacity;
    // 键值表
    HashMap<Integer, Integer> keyToVal;
    // 键和出现频率表
    HashMap<Integer, Integer> keyToFreq;
    // 频率和键表
    HashMap<Integer, LinkedHashSet<Integer>> freqToKeys;
    // 当前最小频率
    int minFreq;

    public LFUCache(int capacity) {
        this.capacity = capacity;
        this.keyToFreq = new HashMap<>();
        this.keyToVal = new HashMap<>();
        this.freqToKeys = new HashMap<>();
        this.minFreq = 0;
    }

    public int get(int key) {
        if (!keyToVal.containsKey(key)) {
            return -1;
        }

        increaseFreq(key);
        return keyToVal.get(key);
    }

    public void put(int key, int value) {

        if (this.capacity <= 0) {
            return;
        }

        // 如果键已存在，那么就更新
        if (keyToVal.containsKey(key)) {
            keyToVal.put(key, value);
            increaseFreq(key);
            return;
        }

        // 如果容量不足，就先移除
        if (capacity <= keyToVal.size()) {
            removeMinFreqVal();
        }

        // 添加新的数据
        keyToVal.put(key, value);
        keyToFreq.put(key, 1);
        freqToKeys.putIfAbsent(1, new LinkedHashSet<Integer>());
        freqToKeys.get(1).add(key);
        // 因为是新添加的，所以该键对应的频率一定是 1
        minFreq = 1;
    }

    private void increaseFreq(Integer key) {
        // 获取当前键的频率
        Integer freq = keyToFreq.get(key);
        // 更新频率
        keyToFreq.put(key, freq + 1);
        // 在当前频率列表中删除键
        freqToKeys.get(freq).remove(key);

        // 在频率加一列表中插入键
        freqToKeys.putIfAbsent(freq + 1, new LinkedHashSet<>());
        freqToKeys.get(freq + 1).add(key);
        // 如果当前频率队列中只有一个待移除键了，就顺手把队列都删了
        if (freqToKeys.get(freq).isEmpty()) {
            freqToKeys.remove(freq);
            // 如果原来的频率是最小频率，那就加一
            if (freq == minFreq) {
                minFreq++;
            }
        }
    }

    private void removeMinFreqVal() {
        // 获取频率最小的列表
        LinkedHashSet<Integer> keyList = freqToKeys.get(minFreq);
        // 获取频率最小列表中最长时间未被访问的键
        Integer key = keyList.iterator().next();
        keyToVal.remove(key);
        keyToFreq.remove(key);
        keyList.remove(key);
        // 如果当前键是改列表中的最后一个数，就把整个列表都移除
        if (keyList.isEmpty()) {
            freqToKeys.remove(minFreq);
        }

    }
}

[710] 黑名单中的随机数

给定一个整数 n 和一个 无重复 黑名单整数数组 blacklist 。设计一种算法，从 [0, n - 1] 范围内的任意整数中选取一个 未加入 黑名单 blacklist 的整数。任何在上述范围内且不在黑名单 blacklist 中的整数都应该有 同等的可能性 被返回。

优化你的算法，使它最小化调用语言内置随机函数的次数。

实现 Solution 类:

Solution(int n, int[] blacklist) 初始化整数 n 和被加入黑名单 blacklist 的整数
int pick() 返回一个范围为 [0, n - 1] 且不在黑名单 blacklist 中的随机整数

示例 1：

输入
["Solution", "pick", "pick", "pick", "pick", "pick", "pick", "pick"]
[[7, [2, 3, 5]], [], [], [], [], [], [], []]
输出
[null, 0, 4, 1, 6, 1, 0, 4]

解释
Solution solution = new Solution(7, [2, 3, 5]);
solution.pick(); // 返回0，任何[0,1,4,6]的整数都可以。注意，对于每一个pick的调用，
              // 0、1、4和6的返回概率必须相等(即概率为1/4)。
solution.pick(); // 返回 4
solution.pick(); // 返回 1
solution.pick(); // 返回 6
solution.pick(); // 返回 1
solution.pick(); // 返回 0
solution.pick(); // 返回 4

提示:

1 <= n <= 109
0 <= blacklist.length <- min(105, n - 1)
0 <= blacklist[i] < n
blacklist 中所有值都不同
pick 最多被调用 2 * 104 次

Related Topics

哈希表

数学

二分查找

排序

随机化

解法一：

黑名单映射

class Solution {

    Map<Integer, Integer> map;
    Random random;
    int index;

    public Solution(int n, int[] blacklist) {
        map = new HashMap<>();
        index = n - blacklist.length;
        random = new Random();

        // 把 index右边的所有 黑名单外的数存到 hashset中
        HashSet<Integer> hashSet = new HashSet<>();
        for (int i = index; i < n; i++) {
            hashSet.add(i);
        }

        for (int i : blacklist) {
            hashSet.remove(i);
        }

        // 把 index左边待 pick的数中 黑名单内的数全部映射到 index右边的不在黑名单中的数
        Iterator<Integer> iterator = hashSet.iterator();
        for (int i : blacklist) {
            if (i < index) {
                map.put(i, iterator.next());
            }
        }
    }

    public int pick() {
        // 仅获取 index左边的数
        int i = random.nextInt(index);
        if (map.containsKey(i)) {
            return map.get(i);
        }

        return i;
    }
}

不用 HashSet

class Solution {

    Map<Integer, Integer> map;
    Random random;
    int index;

    public Solution(int n, int[] blacklist) {
        map = new HashMap<>();
        index = n - blacklist.length;
        random = new Random();

        for (int i : blacklist) {
            map.put(i, 0);
        }

        int last = n - 1;
        for (int i : blacklist) {

            if (i >= index) {
                continue;
            }

            // 不使用 HashSet，而是通过循环找到映射的值
            while (map.containsKey(last)) {
                last--;
            }

            map.put(i, last--);
        }
    }

    public int pick() {
        int i = random.nextInt(index);
        if (map.containsKey(i)) {
            return map.get(i);
        }

        return i;
    }
}

[1373] 二叉搜索树的最大键值和

给你一棵以 root 为根的 二叉树 ，请你返回任意二叉搜索子树的最大键值和。

二叉搜索树的定义如下：

任意节点的左子树中的键值都小于此节点的键值。
任意节点的右子树中的键值都大于此节点的键值。
任意节点的左子树和右子树都是二叉搜索树。

示例 1：
输入：root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出：20
解释：键值为 3 的子树是和最大的二叉搜索树。
示例 2：
输入：root = [4,3,null,1,2]
输出：2
解释：键值为 2 的单节点子树是和最大的二叉搜索树。
示例 3：
输入：root = [-4,-2,-5]
输出：0
解释：所有节点键值都为负数，和最大的二叉搜索树为空。
示例 4：
输入：root = [2,1,3]
输出：6
示例 5：
输入：root = [5,4,8,3,null,6,3]
输出：7
提示：

每棵树有 1 到 40000 个节点。

每个节点的键值在 [-4 * 10^4 , 4 * 10^4] 之间。

Related Topics

树

深度优先搜索

二叉搜索树

动态规划

二叉树

解法一：

解决思想：
如果想要一趟递归完成全部内容，单靠基本数据类型难以达成；
势必需要通过构造对象实现单次返回时传递多个数据；
可以通过后序遍历，自底向上，由零到整进行计算

因此可构造如下对象：

static class ValidBST {
        boolean isBST;
        int min;
        int max;
        int total;

        public ValidBST(boolean isBST, int min, int max, int total) {
            this.isBST = isBST; // 标识是否为 BST
            this.min = min; // 如果是 BST，那么就表示该树中最小的节点的值
            this.max = max; // 如果是 BST，那么就表示该树中最大的节点的值
            this.total = total; // 如果是 BST，那么就表示该树中所有节点的和
        }
    }

整体代码如下：

class Solution {
    // 记录最大值
    int maxVal = 0;

    public int maxSumBST(TreeNode root) {
        traverse(root);
        return maxVal;
    }

    private ValidBST traverse(TreeNode root) {
        // base condition
        if (root == null) {
            return new ValidBST(true, Integer.MAX_VALUE, Integer.MIN_VALUE, 0);
        }

        // 后序遍历
        ValidBST left = traverse(root.left);
        ValidBST right = traverse(root.right);

        // 判断是不是 BST
        if (left.isBST
                && right.isBST
                && root.val > left.max
                && root.val < right.min) {
            // 构造本次递归待返回的值
            ValidBST cur = new ValidBST(true,
                    Math.min(root.val, left.min), // 这是因为在 base condition中，我们的 min=Integer.MAX_VALUE，所以这里需要 Math.min()操作
                    Math.max(root.val, right.max), // 同上
                    root.val + left.total + right.total); 
            maxVal = Math.max(maxVal, cur.total);
            return cur;
        }

        ValidBST cur = new ValidBST(false, 0, 0, 0);
        return cur;
    }

    static class ValidBST {
        boolean isBST;
        int min;
        int max;
        int total;

        public ValidBST(boolean isBST, int min, int max, int total) {
            this.isBST = isBST;
            this.min = min;
            this.max = max;
            this.total = total;
        }
    }
}

[剑指 Offer 51] 数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:
输入: [7,5,6,4]
输出: 5
限制：
0 <= 数组长度 <= 50000
Related Topics

树状数组

线段树

数组

二分查找

分治

有序集合

归并排序

解法一：

归并排序的时候确定逆序对

class Solution {
    int[] tmp;
    public int reversePairs(int[] nums) {
        tmp = new int[nums.length];
        int res =  sort(nums, 0, nums.length - 1);
        System.out.println(Arrays.toString(nums));
        return res;
    }

    private int sort(int[] nums, int left, int right) {
        if (left >= right) {
            return 0;
        }

        int mid = left + (right - left) / 2;
        int cnt = 0;
        cnt += sort(nums, left, mid);
        cnt += sort(nums, mid + 1, right);
        cnt += merge(nums, left, mid, right);
        return cnt;
    }

    private int merge(int[] nums, int left, int mid, int right) {
        for(int i = left; i <= right; i++) {
            tmp[i] = nums[i];
        }

        int cnt = 0;
        int p = left, q = mid + 1;
        for(int i = left; i <= right; i++) {
            if (p >= mid + 1) {
                nums[i] = tmp[q++];
            } else if (q >= right + 1) {
                nums[i] = tmp[p++];
            } else if (tmp[p] > tmp[q]) {
                nums[i] = tmp[q++];
                // 为什么是 mid - p + 1???
                // 因为此时左边数组中的从 i 到 m 的所有数都是大于tmp[j]的
                cnt += (mid - p + 1);
            } else {
                nums[i] = tmp[p++];
            }
        }

        return cnt;
    }
}

题型汇总

一、元素去重

包括字符串中去重、有序数组保留n个重复、有序链表去重

二、前缀和

有连续子数组和的，一般都是前缀和

三、差分数组

有对数组区间统一进行某一加减操作的，就用差分数组；

操作：

计算得到差分数组：diff[i] = nums[i] - nums[i-1];
将对原数组的操作施加到差分数组行，eg: [i, j] +2 -> diff[i] + 2, diff[j+1] - 2，如果 j+1>length，就不用减了
从差分数组恢复，nums[i] = diff[i] + nums[i-1]，因为推断第 i 个值需要先知道第 i-1 个值，所以要从左到右恢复

四、二维数组遍历

遍历左上角：

for(int i = matrix.length-1; i >= 0; i--) {
    for(int j = 0; j <= i; j++) {
        System.out.print(matrix[matrix.length - 1 -i][j] + " ");
    }
    System.out.println();
}

遍历右上角

for(int i = 0; i < matrix.length; i++) {
    for(int j = i; j < matrix.length; j++) {
        System.out.print(matrix[i][j] + " ");
    }
    System.out.println();
}

遍历左下角

for(int i = 0; i < matrix.length; i++) {
    for(int j = 0; j <= i; j++) {
        System.out.print(matrix[i][j] + " ");
    }
    System.out.println();
}

遍历右下角：

for(int i = matrix.length - 1; i >= 0; i--) {
    for(int j = i; j < matrix.length; j++) {
        System.out.print(matrix[matrix.length - 1 - i][j] + " ");
    }
    System.out.println();
}

五、滑动窗口

核心就是 while里面套 while

int left = 0, right = 0;

while (right < s.size()) {
    // 增大窗口
    window.add(s[right]);
    right++;

    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
}

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    
    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 增大窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 缩小窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

针对字符串 s 和字符串 p，如果要在 s中寻找连续的和 s一样长的子串，那么里面的那个 while的条件可以是 while(right - left >= s.length())，如 567，438；

但如果是求的 s中的子串可能比 p长一点的话，while条件就可以设为 while(valid == need.size())，如 76

六、概率事件/按权重取值

会先给你一串数字，nums[i] 就是取到 i值的概率, 即 nums[i]/sum，求随机取值的结果。

做法是将 nums[i] 转换成前缀和数组，那么 preSum[n-1]就一定是最大值，然后 random.nextInt(preSum[n-1])，得到target，再回到 preSum数组中进行二分查找，找它的右边界，右边界下标就是 i

class Solution {

    int[] preSum;
    Random random;
    int len;

    public Solution(int[] w) {
        len = w.length;
        preSum = new int[len];
        preSum[0] = w[0];
        for(int i = 1; i <len; i++) {
            preSum[i] = preSum[i-1] + w[i];
        }
        random = new Random();
    }
    
    public int pickIndex() {
        int target = random.nextInt(preSum[len - 1]);
        int left = 0, right = len;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (preSum[mid] == target) {
                left = mid + 1;
            } else if (preSum[mid] > target) {
                right = mid;
            } else if (preSum[mid] < target) {
                left = mid + 1;
            }
        }

        return left;
    }
}

七、水塘抽样

用通俗的语言说一下：

如果我们池子中只有一个数字，那么拿到第一个数字的概率就是100%毋庸置疑。
两个数字50% 三个数字每个数字的几率都是33% 以此类推。。。。

当我们不知道池子里有多少个数字的时候，就需要用蓄水池的算法思想去计算。

当链表前行到第一个数字，此时取第一个数字的几率为100%，那result自然等于这个数字。
前进到第二个数字，那么此时取这个数字的几率自然就为50%（池子里只有两个数字），那么就是50%的几率取新数字，50%的几率保留原本的数字。
第三个数字的时候，33%的几率取当前最新的这个数字，66%的几率保留原本的数字。这66%中：原本的数字有50%的几率是1，有50%的几率是2。也就是此时三个数字的概率都为33%。通过这个算法，就能达到取数的概率均摊，从而实现随机。

我们可以设计如下算法：

从链表头开始，遍历整个链表，对遍历到的第 i 个节点，随机选择区间 [0,i) 内的一个整数，如果其等于 0，则将答案置为该节点值，否则答案不变。

class Solution {

    ListNode head;
    Random random;

    public Solution(ListNode head) {
        this.head = head;
        random = new Random();
    }
    
    public int getRandom() {
        ListNode node = head;
        int idx = 1, res = 0;
        while (node != null) {
            if (random.nextInt(idx) == 0) {
                res = node.val;
            }
            idx++;
            node = node.next;
        }
        return res;
    }
}

八、二分查找

首先是二分查找，找左右边界

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] arr = new int[2];
        arr[0] = searchLeft(nums, target);
        arr[1] = searchRight(nums, target);
        return arr;
    }

    public int searchLeft(int[] nums, int target) {
        int left = 0, right = nums.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid;
            }
        }
		// 无论是找左边界还是有边界，都应当注意跳出循环时的具体条件是什么
        // 像这里就是 left == right(二者都是一个一个加减的，所以一定是在相等的时候退出循环)
        // 假设数组为 [2, 2]，target = 3，你找左边界，那么这个左边界找出来就是 2(不存在)，因此需要做出如下判断
        if (left >= nums.length || nums[left] != target) {
            return -1;
        }

        return left;
    }

    public int searchRight(int[] nums, int target) {
        int left = 0, right = nums.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            }

        }

        // 同上，针对 [2, 2] target=1，找右边界，找出来的就是 -1(right - 1 = -1, right = 0)
        if (right <= 0 || nums[right - 1] != target) {
            return -1;
        }

        return right - 1;
    }
}

然后其实难的地方在于将问题抽象成二分查找，一般来说，看到 O(NlogN) 或者求最大值的最小值，使最大值尽可能小这种话，就思考二分查找

特别是见 410 和 1011

九、最近公共祖先

也就是求二叉树中两个节点的最近公共祖先节点。

做法是从 root开始寻找递归地找 p || q，如果自己就是 p 或 q，就直接返回；否则找左右子树，如果刚好左右子树都返回非 null的值，那么当前节点就一定是最近公共祖先；否则就返回那个不是 null的节点

见 235，236，1644，1650，1676

十、二叉搜索树

注意那两道【不同二叉搜索树】的题

95，96

十一、排序

见 912

归并排序

化整为零，再由零构建整

在由零到整的过程中，可以动态的判断很多元素间的关系，见 315 和剑指 offer 51

快速排序

先定位第一个元素在数组中的位置，并通过交换保证其左边的元素都比它小，右边的元素都比它大，然后再拆分问题，左右分别递归

归并排序中的核心算法是 merge()，快速排序中的核心部分就是 partition

见 215

十二、最长子序列

一般都是 dp

看清楚题目问的是什么，明确 dp的 base case，有时候是 0，有时候序号累加等等，看清楚

int[][] dp = new int[s1.length() + 1][s2.length() + 1];

// base case


for(int i = 1; i <= s1.length(); i++) {
    for(int j = 1; j <= s2.length(); j++) {
        if (s1.charAt(i) == s2.charAt(j)) {
            dp[i][j] = xxx;
        } else {
            // 或者是 max
            dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]);
        }
    }
}

见 583，1143，300，712

另外，求字符串的最长回文子序列的时候，别搞七搞八的，就直接把字符串反转后求两个字符串的最长公共子序列就行了

十三、背包

0、1背包问题

每种物品最多只能放一次，也就是说包里没有重复的东西

注意点：先循环【物品】再循环【背包】

判断最多能放多少价值

int [][] dp = new int[V + 1][W + 1];
for(int i = 1; i <= V; i++) { // 货物种类
    for (int j = 1; j <= W; j++) { // 背包的重量
        if ((j - w[i]) < 0) {
            // 放不下
            dp[i][j] = dp[i-1][j];
        } else {
            // 判断是放好还是不放好
            dp[i][j] = Math.max(
                dp[i - 1][j - w[i - 1]] + val[i - 1], 
                dp[j - 1][j]);
        }
    }
    
}
 return dp[V][W];

判断是否能放到指定的价值

boolean[][] dp = new boolean[V + 1][W + 1];
// 放到包里只有 0元，肯定都能实现
for (int i = 0; i <= V; i++) {
    dp[i][0] = true;
}

for (int i = 1; i <= V; i++) {
    fot (int j = 1; j <= W; j++) {
        if (j - w[i - 1] < 0) {
            dp[i][j] = dp[i-1][j];
        } else {
            dp[i][j] = dp[i-1][j] || dp[i-1][j - w[i-1]];
        }
    }
}

return dp[i][j];

如果采用一维数组，当物品只能取一次时，从后往前遍历 weight；物品能取多次时，从前往后遍历 weight

boolean[] dp = new boolean[W + 1];
dp[0] = true;

for (int i = 1; i <= V; i++) {
    for (int j = W; j >= 0; j--) {
        if (j - w[i-1] >= 0) {
            dp[j] = dp[j] || dp[j - w[i-1]];
        }
    }
}
return dp[W];

见 416

完全背包

物品的数量无限，可以放多个重复的东西

这个就正序访问即可

注意是【求数量】还是【求是否】

另外注意 base case的设置

二维：

class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp = new int[coins.length + 1][amount + 1];
        for (int i = 0; i <= coins.length; i++) {
            dp[i][0] = 1;
        }

        for(int i = 1; i <= coins.length; i++) {
            for (int j = 1; j <= amount; j++) {
                if (j - coins[i-1] < 0) {
                    dp[i][j] = dp[i-1][j];
                } else {
                    dp[i][j] = dp[i-1][j] + dp[i][j - coins[i-1]];
                }
            }
        }

        return dp[coins.length][amount];
    }
}

一维：

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];

        dp[0] = 1;
        for (int i = 1; i <= coins.length; i++) {
            for (int j = 1; j <= amount; j++) {
                if (j - coins[i-1] >= 0) {
                    dp[j] += dp[j - coins[i - 1]];
                }
            }
        }

        return dp[amount];
    }
}

总结：

0，1背包从右向左，注意 dp[0]，双重循环 for (int x : value) {for (int i = x; i <= weight; i++) {}} 或 for (int x :value) {for (int i = weight; i >= x; i--){}}，如果求是否 dp[i] = dp[i] || dp[i-x]

十四、打家劫舍

dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1])

就是普通的 dp，声明 dp数组的时候最好给 length + 1；

环形数组打劫两次，数的话因为分叉，所以打劫的时候多算一点

见 337，213，198

十五、买卖股票

买卖Ⅰ，只能交易一次

class Solution {
    public int maxProfit(int[] prices) {
       int buy = Integer.MIN_VALUE, sell = 0;
       for(int x : prices) {
           // 0 - x 表示：我本次买的话，买完之后剩的钱，因为只能买一次，所以之前没有钱!
           // 买了之后，手里的钱还有多少，因为只能买一次，所以就是 0 - x(你原来没有钱，就是 0)
           buy = Math.max(buy, 0 - x);
           // x + buy 表示：我本次卖的话，卖完之后剩的钱(注意，buy是负数)
           // 卖了之后，手里的钱还能有多少，就是上一次买的钱 + x
           sell = Math.max(sell, buy + x);
       }

       return sell;
    }
}

买卖Ⅱ，可以交易无数次

class Solution {
    public int maxProfit(int[] prices) {
       int buy = Integer.MIN_VALUE, sell = 0;
       for(int x : prices) {
           // 买了之后，手里的钱还有多少，而买之前的钱就算上一次卖掉剩下的钱，刚好 sell初始的时候也是 0
           buy = Math.max(buy, sell - x);
           // 卖了之后，手里的钱还能有多少，就是上一次买的钱 + x
           sell = Math.max(sell, buy + x);
       }

       return sell;
    }
}

买卖Ⅲ,，只能交易两次

class Solution {
    public int maxProfit(int[] prices) {
        // 第一、二次的买
        int b1 = Integer.MIN_VALUE, b2 = Integer.MIN_VALUE;
        // 第一、二次的卖
        int s1 = 0, s2 = 0;

        for(int x : prices) {
            b1 = Math.max(b1, -x);
            s1 = Math.max(s1, b1+x);
            b2 = Math.max(b2, s1-x);
            s2 = Math.max(s2, b2+x);
        }

        return s2;
    }
}

class Solution {
    public int maxProfit(int[] prices) {
        int[] buy = new int[2 + 1];
        int[] sell = new int[2 + 1];
        for(int i = 0; i <= 2; i++) {
            buy[i] = Integer.MIN_VALUE;
            sell[i] = 0;
        }

        for(int x : prices) {
            for(int i = 1; i <= 2; i++) {
                buy[i] = Math.max(buy[i], sell[i-1] - x);
                sell[i] = Math.max(sell[i], buy[i] + x);
            }
        }

        return sell[2];
    }
}

买卖股票Ⅳ，能交易 K次

class Solution {
    public int maxProfit(int k, int[] prices) {
        // 注意这个 k 值的更新
        k = Math.min(k, prices.length);
        
        int[] buy = new int[k+1];
        int[] sell = new int[k+1];
        for(int i = 0; i <= k; i++) {
            buy[i] = Integer.MIN_VALUE;
            sell[i] = 0;
        }

        for(int x : prices) {
            for(int i = 1; i <= k; i++) {
                // i - 1 说明是上一次
                buy[i] = Math.max(buy[i], sell[i-1] - x);
                // i 说明是针对本次
                sell[i] = Math.max(sell[i], buy[i] + x);
            }
        }

        return sell[k];
    }
}

买卖股票，能交易无穷次，但是卖后第二天不能再买

class Solution {
    public int maxProfit(int[] prices) {
        int buy = Integer.MIN_VALUE;
        int sell = 0, last_sell = 0;

        for(int x : prices) {
            // 使用上上次卖后的钱
            buy = Math.max(buy, last_sell - x);
            // 记忆上次卖的钱
            last_sell = sell;
            // 更新本次卖的钱
            sell = Math.max(sell, buy + x);
        }

        return sell;
    }
}

买卖股票，无限次，但是每笔交易需要教费(一整次的买卖)

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int buy = Integer.MIN_VALUE;
        int sell = 0;

        for(int x : prices) {
            // 买的时候正常买
            buy = Math.max(buy, sell - x);
            //  卖的时候多付点钱
            sell = Math.max(sell, buy + x - fee);
        }

        return sell;
    }
}

十六、区间调度

区间问题记得画图+排序，基本都是贪心

重叠区间尽可能少/多

按照区间的左右端之一排序，然后判断当前的右端点与下一个区间的左端点的大小来判断是否重叠

画个图

见 435、452

求某一时刻重叠区间最多是多少

将开始和结束时间拆开来分别排序，然后判断

见 253

十八、跳跃游戏

贪心算法

就看好眼前就行

像买股票一样把答案背下来

见 45、55

十九、LRU 和 LFU

除了 Map，其它都要自己构造；

自己构造 Node，自己构造双向链表；

LRU

class LRUCache {
    // 必须构造成 Node形式，并且在 Map中存 Node，否则无法做到 O(1)的删除
    class Node {
        Integer key;
        Integer value;
        Node prev, next;

        public Node(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }

    // 必须是双向链表，否则没办法立刻把一个 Node删掉
    class DoubleList {
        
        Node head, tail;

        public DoubleList() {
            head = new Node(-1, -1);
            tail = new Node(-1, -1);
            head.next = tail;
            head.prev = null;
            tail.prev = head;
            tail.next = null;
        }

        private void remove(Node v) {
            v.prev.next = v.next;
            v.next.prev = v.prev;
            v.prev = null;
            v.next = null;
        }

        private void addFirst(Node v) {
            v.next = head.next;
            head.next.prev = v;
            v.prev = head;
            head.next = v;
        }

        private Node removeLast() {
            if (tail.prev == head) {
                return null;
            }

            Node v = tail.prev;
            remove(v);
            return v;
        }

    }

    int capacity;
    DoubleList recently_list;
    Map<Integer, Node> key_value;
    int curCnt;


    public LRUCache(int capacity) {
        this.capacity = capacity;
        this.recently_list = new DoubleList();
        this.key_value = new HashMap<>();
        this.curCnt = 0;
    }
    
    public int get(int key) {
        if (!key_value.containsKey(key)) {
            return -1;
        }

        Node v = key_value.get(key);
        recently_list.remove(v);
        recently_list.addFirst(v);
        return v.value;
    }
    
    public void put(int key, int value) {
        if (key_value.containsKey(key)) {
            Node v = key_value.get(key);
            v.value = value;
            recently_list.remove(v);
            recently_list.addFirst(v);
            return;
        }

        if (curCnt >= capacity) {
            Node v = recently_list.removeLast();
            key_value.remove(v.key);
        }

        Node v = new Node(key, value);
        recently_list.addFirst(v);
        key_value.put(key, v);
        curCnt++;
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

LFU

class LFUCache {

    class Node {
        Integer key;
        Integer value;
        Integer freq;

        public Node(Integer key, Integer value) {
            this.key = key;
            this.value = value;
            this.freq = 0;
        }
    }

    Map<Integer, Node> key_value;
    Map<Integer, LinkedList<Node>> freq_nodes;
    int capacity;
    int minFreq;

    public LFUCache(int capacity) {
        this.capacity = capacity;
        minFreq = 0;
        key_value = new HashMap<>();
        freq_nodes = new HashMap<>();
    }

    private void increase(Node v) {
        // 在原队列中移除
        freq_nodes.get(v.freq).remove(v);
        // 判断是否为最小的频率
        if (v.freq == minFreq && freq_nodes.get(minFreq).isEmpty()) {
            minFreq++;
        }

        // 增加频率，并且插入到新的队列中去
        v.freq++;
        if (!freq_nodes.containsKey(v.freq)) {
            freq_nodes.put(v.freq, new LinkedList<Node>());
        }
        freq_nodes.get(v.freq).addFirst(v);
    }

    private Node removeLast() {
        Node v = freq_nodes.get(minFreq).removeLast();
        key_value.remove(v.key);
        // if (freq_nodes.get(minFreq).isEmpty()) {
        //     minFreq++;
        // }
        return v;
    }

    private void addNode(Node v) {
        if (!freq_nodes.containsKey(v.freq)) {
            freq_nodes.put(v.freq, new LinkedList<Node>());
        }
        freq_nodes.get(v.freq).addFirst(v);
        key_value.put(v.key, v);
    }
    
    public int get(int key) {
        // 不存在该 key
        if (!key_value.containsKey(key)) {
            return -1;
        }

        // 获取该 key对应的 Node
        Node v = key_value.get(key);
        increase(v);
        
        return v.value;
    }
    
    public void put(int key, int value) {
        // 容量判断
        if (this.capacity <= 0) {
            return;
        }

        // key是否已存在
        if (key_value.containsKey(key)) {
            Node v = key_value.get(key);
            v.value = value;
            increase(v);
            return;
        }

        // 是否已经满了
        if (capacity == key_value.size()) {
            removeLast();
        }

        // 新增节点
        Node v = new Node(key, value);
        v.freq = 1;
        minFreq = 1;
        addNode(v);
    }
}

/**
 * Your LFUCache object will be instantiated and called as such:
 * LFUCache obj = new LFUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

二十、队列实现栈、栈实现队列

队列实现栈时，需要一个队列和一个成员变量 top

class MyStack {

    Queue<Integer> queue;
    int top;

    public MyStack() {
        queue = new LinkedList<>();
    }
    
    public void push(int x) {
        queue.offer(x);
        top = x;
    }
    
    public int pop() {
        int size = queue.size();
        for(int i = 0; i< size - 1; i++) {
            push(queue.poll());
        }
        return queue.poll();
    }
    
    public int top() {
        return this.top;
    }
    
    public boolean empty() {
        return queue.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

栈实现队列，需要两个栈，一个用来临时存放元素

class MyQueue {

    Stack<Integer> stack;
    Stack<Integer> tmp;
    int peek;

    public MyQueue() {
        stack = new Stack<>();
        tmp = new Stack<>();
    }
    
    public void push(int x) {
        if (stack.isEmpty()) {
            peek = x;
        }
        stack.push(x);

    }
    
    public int pop() {
        int size = stack.size();
        for(int i = 0; i < size - 1; i++) {
            tmp.push(stack.pop());
        }
        int retVal = stack.pop();
        while(!tmp.isEmpty()) {
            push(tmp.pop());
        }

        return retVal;
    }
    
    public int peek() {
        return peek;
    }
    
    public boolean empty() {
        return stack.isEmpty();
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

二十一、单调栈

寻找下一个最大/最小的题，就思考单调栈；

从后往前遍历，在栈非空的情况下，将小于自己/大于自己的元素全部清除，保证里面都是大于自己/小于自己的元素；

然后存起来；最后再把自己push到单调栈中；

见 496、739、503，针对循环数组，如果最多也就访问两遍的话，可以将其抽象为 2 * length 的长度，遍历 0 ~ 2 * length，然后 % length

单调队列也相似，针对队列中比自己小的，也都出栈；其实所谓的单调队列是 Deque双端队列才对

见 239

二十二、图

图不太会考，如果考了直接摆烂；

主要考虑两点：

图的构建，一般使用 List<Integer>[] graph = buildGraph(...);
遍历时防止重复，需要一个 visited[]数组，然后有时候为了回溯，会再额外来一个 onpath[]

见课程表 207

二十三、回溯

有两种回溯：

自上而下的回溯，那么不需要 visited数组
每次回溯都要全部遍历一遍，然后根据 visited判断

但不管如何，回溯的加和减这两种操作都是放在循环里面的

见 51、46

处理排列/组合/子集问题

元素无重且不可复选

/* *
* 组合/子集问题回溯算法框架 
*/
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}

/**
* 排列问题回溯算法框架 
*/
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

元素有重且不可复选

Arrays.sort(nums);
/**
* 组合/子集问题回溯算法框架 
*/
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 剪枝逻辑，跳过值相同的相邻树枝
        if (i > start && nums[i] == nums[i - 1]) {
            continue;
        }
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}


Arrays.sort(nums);
/**
* 排列问题回溯算法框架
*/
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 剪枝逻辑，固定相同的元素在排列中的相对位置
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

元素无重但可复选

/**
* 组合/子集问题回溯算法框架 
*/
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i);
        // 撤销选择
        track.removeLast();
    }
}


/**
* 排列问题回溯算法框架 
*/
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        backtrack(nums);
        // 撤销选择
        track.removeLast();
    }
}

posted @ 2021-02-01 12:37 小么VinVin 阅读(332) 评论(0) 编辑收藏举报

刷新页面返回顶部

YuanChuZiWen

Less Is More

力扣刷题

力扣刷题

简单难度

[1] 两数之和

[7] 整数反转

解法一：

解法二：

[20] 有效括号

解法一

解法二

解法三

[21] 合并两个有序链表

解法一：

解法二

[26] 删除有序数组中的重复项

[27] 移除元素

解法一：

♥ [28] 实现 strStr()

解法一：

❤ 解法二：

[34] 在排序数组中查找元素的第一个和最后一个位置

解法一：

解法二：

[66] 加一

解法一：

[70] 爬楼梯

解法一：

[83] 删除排序链表中的重复元素

解法一：

解法二：

[88] 合并两个有序数组

解法一：

解法二：

[94] 二叉树的中序遍历

解法一：

❤ 解法二：

❤ 解法三：

[98] 验证二叉搜索树

解法一：

解法二：

[100] 相同的树

解法一：

[101] 对称二叉树

解法一：

解法二：

解法三：

[104] 二叉树的最大深度

解法一：

❤ 解法二：

[108] 将有序数组转换为二叉搜索树

解法一：

[111] 二叉树的最小深度

解法一：

解法二：

[114] 二叉树展开为链表

解法一：

[118] 杨辉三角

解法一：

[121] 买卖股票的最佳时机

解法一：

[125] 验证回文串

解法一：

解法二：

♥ [136] 只出现一次的数字

解法一：

♥ 解法二：

[141] 环形链表

[144] 二叉树的前序遍历

[145] 二叉树的后序遍历

解法一：

[155] 最小栈

解法一：

解法二：

[160] 相交链表

解法二：

[169] 多数元素

[190] 颠倒二进制位

解法一：