第四章学习小结心得

一、知识小结

　　         

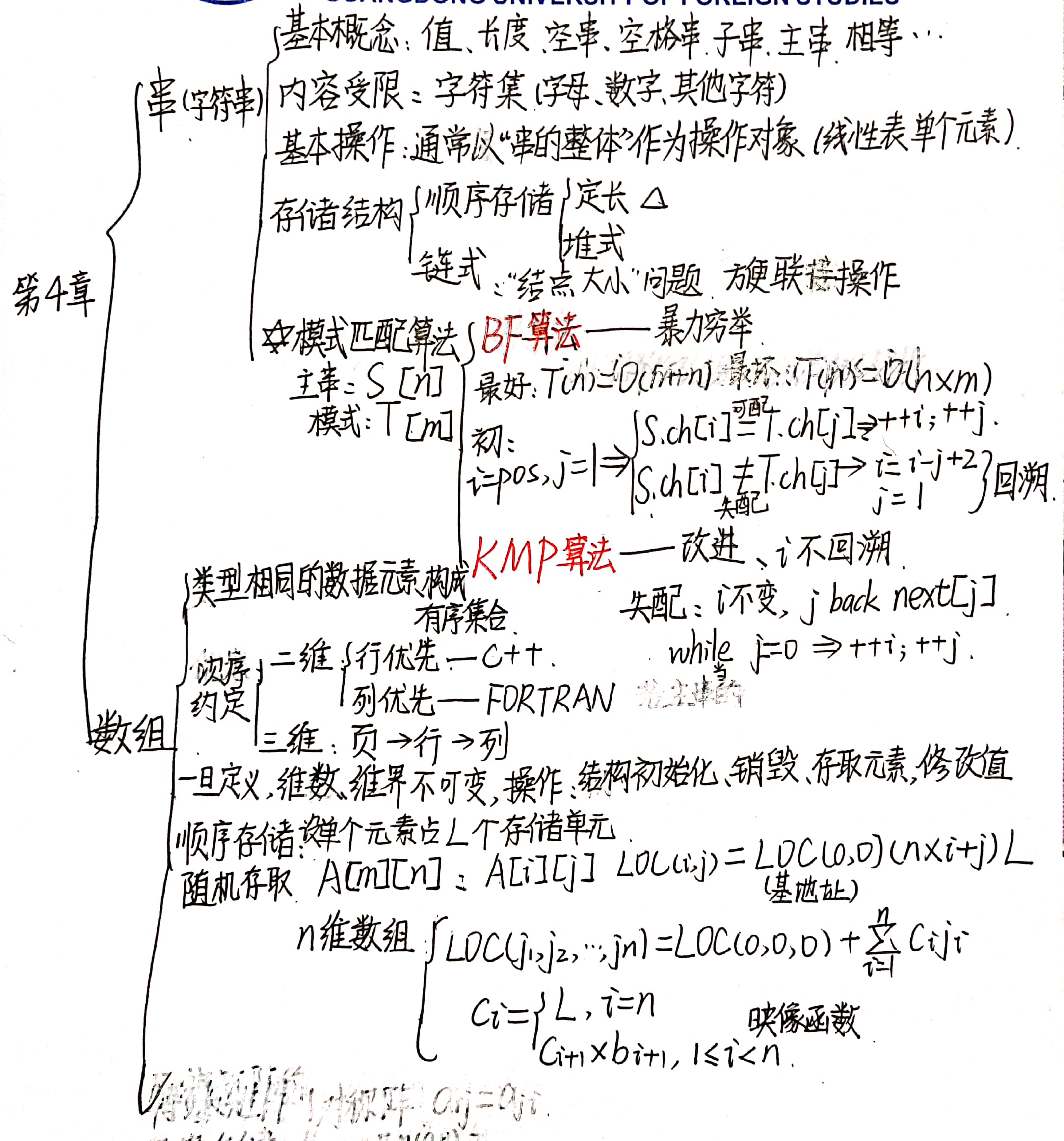
（懒得用键盘敲，手写）

二、解题心得体会

题目：实践——7-1 稀疏矩阵

 稀疏矩阵的压缩存储方式：三元组，十字链表

#define MAX 500
typedef int datatype;
typedef struct{       //定义三元组类型
    int i, j;      //存储非零元素的行标和列标  
    datatype e;    //非零元素值
}SPNode;    
typedef struct{
    int mu, nu, tu;    //矩阵的行、列和非零元素个数
    SPNode data[MAX];    //三元组表
}SPNode;

typedef struct OLNode{
    int i, j;    //行标、列标
    datatype e;    //非零元素的值 
    struct OLNode *right, *down;    //指针域 
}OLNode, *OLink;
typedef struct{
    OLink *Rhead, *Chead;
    int mu, nu, tu;    //稀疏矩阵的行数、列数、非零元个数 
}CrossList; 

以下为正确答案的代码：

#include<iostream>
using namespace std;

#define MAX 500
typedef struct Matrix{
    int row[MAX], col[MAX]; //一维数组存储非零元素的行标、列标
    int e[MAX]; //一维数组存储非零元素的值
}Matrix;


int main()
{
    Matrix M;
    int m, n, N, t[MAX][2];
    cin >> m >> n >> N;
    
    int i(0), j(0), k;
    for(k=0; k<N; k++)
    {
        cin >> M.row[i] >> M.col[j] >> M.e[k];
        t[k][0] = M.row[i];    t[k][1] = M.col[j];
        i++;    j++;
    }
    
    int x;
    cin >> x;
    for(k=0; k<N; k++)
    { //遍历比对法
            if(x==M.e[k]){  //输出元素的位置后退出循环
            cout << t[k][0] <<" "<< t[k][1];
            break;
        }
    }
    if(k==N)    cout <<"ERROR"; //k不存在
    return 0; 
}

上述代码是基于C++基础之上编写出的代码，主函数没有足够的接口，导致主函数冗余，可读性不强，以下为改进后的代码：

#include<iostream>
using namespace std;

#define MAX 500
typedef int ElemType;
typedef struct
{
    int row;        //行号
    int col;        //列号
    ElemType d;     //元素值
} TupNode; //三元组定义
//定义三元组线性表存储结构
typedef struct
{
    int rows;                   //行数值
    int cols;                   //列数值
    int nums;                   //非零元素个数
    TupNode data[MAX];      //data数据域
} TSMatrix; //三元组顺序表定义

void CreateMat(TSMatrix &t, int m, int n, int N)
{ //创建一个有m行n列N个非零元素的稀疏矩阵t， 
    t.rows = m;        t.cols = n;        t.nums = N;
    int i(0), j(0);
    for(i; i<N; i++)
        cin >> t.data[i].row >> t.data[i].col >> t.data[i].d;
}

void Research(TSMatrix &t, int x, int N)
{ //在含有N个非零元素的矩阵t中寻找元素x，
    //若查找成功，则输出所在的行数和列数
    //若查找失败，则输出“ERROR” 
    int i;
    for(i=0; i<N; i++)
    {
        if(x==t.data[i].d)
        {
            cout << t.data[i].row <<" "<< t.data[i].col;
            break;
        }
    }
    if(i==N)
        cout <<"ERROR";
}
int main()
{
    TSMatrix t;
    int m, n, N;
    cin >> m >> n >> N;
    CreateMat(t, m, n, N);
    
    int x;
    cin >> x;
    Research(t,x,N);
    return 0; 
}

矩阵在线性代数中是一个表，在C++中是二维数组，在数据结构中又可以被压缩为一维数组。

同一个知识点，在不同的学习阶段可以有不同的理解，学习的进展越深，越接近其本质，或许这就是循序渐进的学习奥义吧。