机器学习实践（二）：k-NN算法

两种监督机器学习问题

许多算法都有分类和回归两种形式

• 分类：预测类别标签
  • 二分类：两个类别之间区分
    • 正类：需要获得的一类
    • 反类：不需要的一类
  • 多分类：两个以上的类别区分
• 回归：预测一个连续值（浮点数或实数），这个值在给定范围内任意取值，不必精确到某一个基体数值

术语

泛化：如果一个模型可以对新数据做出准确预测，那么可以说该模型能够从训练集泛化到测试集，预测精度即为泛化精度

拟合：模型预测时对训练集的依赖

• 当模型较为复杂、过分关注细节，在训练集中预测表现很好但不能泛化到新数据时，称之为过拟合
• 当模型过于简单，无法抓住数据的全部内容和变化，在训练集上表现很差，称之为欠拟合

总的来说，模型越复杂，在训练数据上的预测结果就越好；但如果模型过于复杂，
去过多关注训练集中每个单独的数据点，模型就不能很好地泛化到新数据上。因此，二者之间存在一个最佳位置，可以得到最佳的泛化性能，这就是我们需要的模型

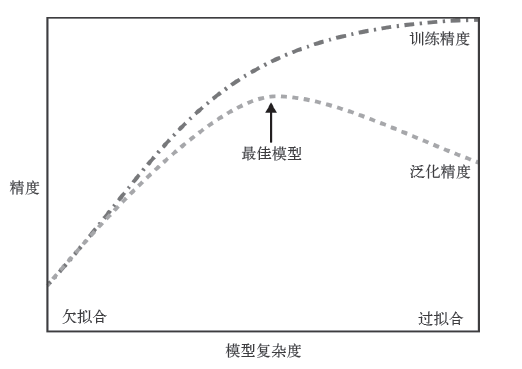
模型复杂度和数据集大小的关系：数据集中包含的数据点的变化范围越大，在不发生过拟合的前提下模型就越复杂（相同或相似的数据点除外）

其他属于补充：

• 特征较少的数据集：低维数据集
• 特征较多的数据集：高维数据集（不同维度的数据集中得出的结论可能是不同的，互相不适用）
• 特征与特征的乘机也可以作为特征——特征工程：包含导出特征的方法

k-NN算法——人云亦云

一种非参、惰性的算法模型：模型本身不会对数据做任何假设，模型结构贴合数据，且训练数据的过程很快

k近邻分类

预测过程

给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中

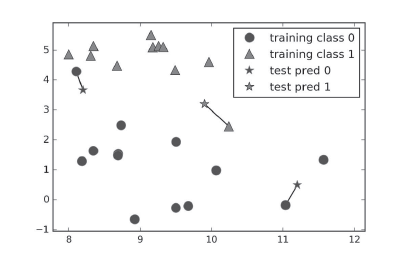
图解：单一近邻是k-NN最简单的版本，只需考虑最近距离的点。分类结果就是最近的训练集中的点所在的分类

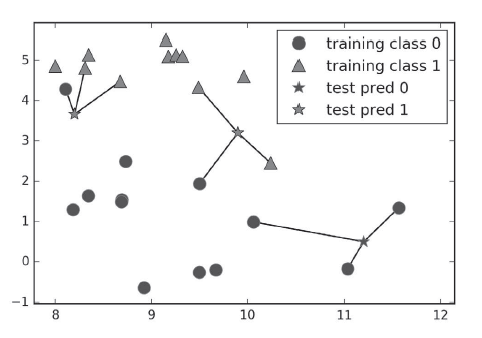
图解：任意(k)个邻居时，采用投票法指定标签，即k个邻居中分类比例占多数的为最后的预测结果

KNeighborsClassifier的决策边界

如果是二维数据集，可以再xy平面上画出所有可能的预测结果，根据点的所属类别对平面着色，这样就可以查看决策边界

from sklearn.model_selection import train_test_split
import mglearn
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

X, y = mglearn.datasets.make_forge()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = KNeighborsClassifier(n_neighbors=3)
clf.fit(X_train, y_train)
print(clf.predict(X_test))
print('{:.2}'.format(clf.score(X_test, y_test)))
fig, axes=plt.subplots(1, 3, figsize=(10, 3))
for n_neighbors, ax in zip([1, 3, 9], axes):
    clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title("{} neighbor(s)".format(n_neighbors))
    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")
    axes[0].legend(loc=3)
p1=plt.scatter(X[y==0,0], X[y==0, 1], color='blue')
p2=plt.scatter(X[y==1,0], X[y==1, 1], color='green')
p3=plt.scatter(X[y==2,0], X[y==2, 1], color='red')
plt.show()

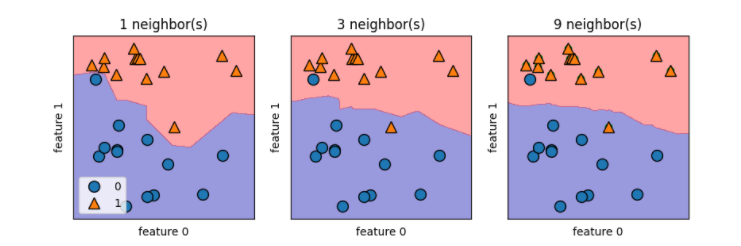
图解：当单一邻居决策时，边界紧挨着训练数据点，边界很陡峭；当邻居越来越多，边界越平滑。而更平滑的边界对应的模型也就更简单

模型复杂度和泛化能力的关系

import numpy as np
import mglearn
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=66)
training_accuracy = []
test_accuracy = []
neighbors_settings = range(1, 11)
for n_neighbors in neighbors_settings:
    clf = KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train, y_train)
    training_accuracy.append(clf.score(X_train, y_train))
    test_accuracy.append(clf.score(X_test, y_test))

plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()
plt.show()

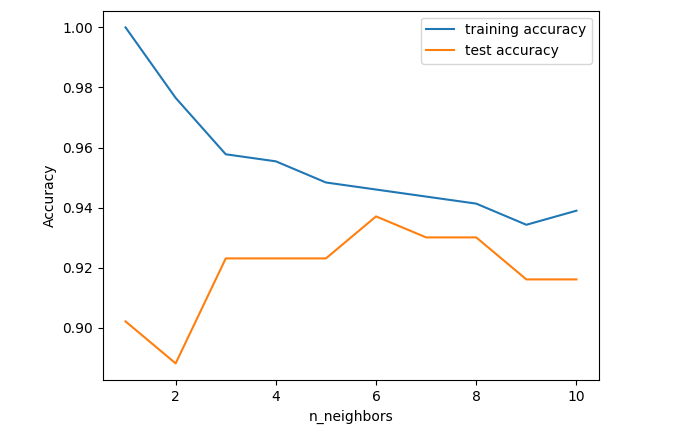
图解：

• 当单一邻居时，训练集的预测结果十分准确，而测试集精度很低。这边是单一近邻的模型过于复杂

• 随着邻居增多，模型变得简单，训练集的精度逐渐下降。当近邻达到10时，模型又过于简单，性能变差

• 最佳的性能在中间的某一处，途中大概在6处，测试集与训练集预测结果最为接近

k近邻回归

import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_knn_regression(n_neighbors=1)
plt.show()

单个和多个近邻预测结果如下：

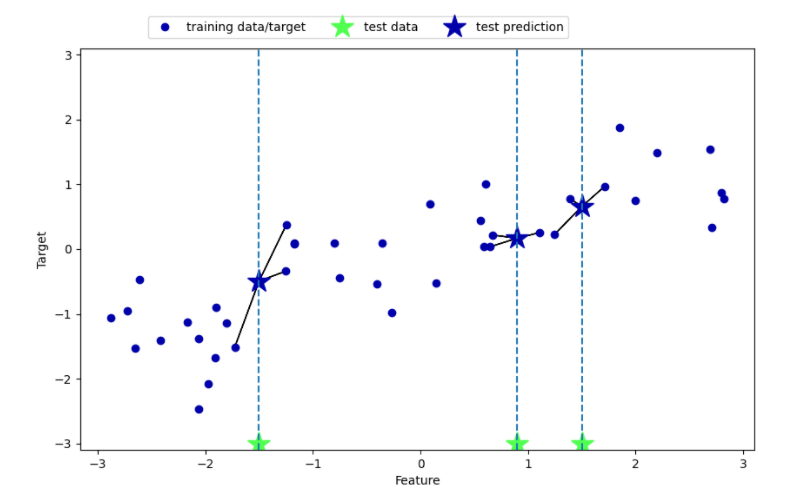
sklearn中KNeighborsRegressor类实现回归

from sklearn.neighbors import KNeighborsRegressor
import mglearn
from sklearn.model_selection import train_test_split

X, y = mglearn.datasets.make_wave(n_samples=40)
# 将wave数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 模型实例化，并将邻居个数设为3
reg = KNeighborsRegressor(n_neighbors=3)
# 利用训练数据和训练目标值来拟合模型
reg.fit(X_train, y_train)

# 预测测试集
print("Test set predictions:\n{}".format(reg.predict(X_test)))

# 评估模型，返回的是R2分数
print("Test set R^2: {:.2f}".format(reg.score(X_test, y_test)))

回归模型同样适用score方法来评估模型，返回的是R2分数，R2分数就是决定系数，是回归模型预测的优度度量，位于1~0之间，当为1时就是完美预测，等于0就是常数模型，即只能预测训练集的平均值

分析KNeighborsRegressor

from sklearn.neighbors import KNeighborsRegressor
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

X, y = mglearn.datasets.make_wave(n_samples=40)
# 将wave数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# 创建1000个数据点，在-3和3之间均匀分布
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
    # 利用1个、3个或9个邻居分别进行预测
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train, y_train)
    ax.plot(line, reg.predict(line))
    ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
    ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
    ax.set_title("{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(n_neighbors, reg.score(X_train, y_train),
    reg.score(X_test, y_test)))
    ax.set_xlabel("Feature")
    ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target","Test data/target"], loc="best")

plt.show()

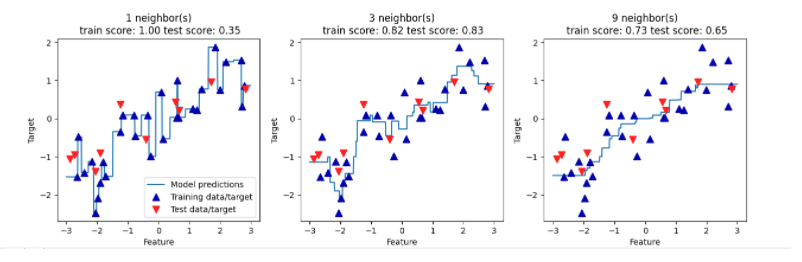
图解：单一邻居时，训练集的每个点都对预测结果有显著影响，预测结果的图像经过所有数据点，这样并不稳定；邻居多的时候，预测结果更为平滑，但对训练数据的拟合不好

总结：kNeighbors分类似的重要参数：邻居个数、数据点之间的距离度量方法。度量方法一般使用 欧式距离 ，即直线距离

• 优点：构建模型简单，容易理解，调整参数不多，性能也够
• 缺点：当数据量（特征多或样本数大）较大时，预测速度较慢。需要对数据进行预处理，对特殊的数据集效果不太好