20172332 2017-2018-2 《程序设计与数据结构》第九周学习总结
20172332 2017-2018-2 《程序设计与数据结构》第九周学习总结
教材学习内容总结
第十五章 图
- 1.无向图是一种边为无序结点对的图:(A,B)与(B,A)的含义是完全一样的。
- 2.如果图中的两个顶点之间有一条连通边,则称这两个顶点是邻接的。(邻接必须有边,否则不叫邻接)
- 3.连通一个顶点及其自身的边称为自循环(A,A)
- 4.如果无向图拥有最大数目的连通顶点的边,则认为这个无向图是完全的。(任意两个顶点之间都会有一条边)
- 5.n个顶点的无向图,要使该图为完全的,要求有n(n-1)/2条边。(不算重复的边)
- 6.路径:图中的一系列边,从一个顶点到另一个顶点的边所组成。
- 7.无向图中路径是双向的。
- 8.路径的长度=该路径中边的条数=顶点数-1。
- 9.如果无向图中的任意两个顶点之间都存在一条路径,则认为这个无向图是连通的。
- 10.环路是一种首顶点和末顶点相同且没有重边的路径。没有环路的图称为无环的。
- 11.无向树是一种连通的无环无向图,其中一个元素被指定为树根。
- 12.有向图(双向图):一种边为有序顶点对的图。(A,B)和(B,A)是不同的边。
- 13.有向图的路径不是双向的。
- 14.拓扑序:有向图中没有环路,且有一条从A到B的边,这可以把顶点A安排在顶点B之前,这种排列得到的顶点次序。
- 15.有向树的附加属性:
- (1)不存在其他顶点到树根的连接。
- (2)每个非树根元素恰好有一个连接。
- (3)树根到每个其他顶点都有一条路径。
- 16.网络(加权图):每条边都带有权重或代价的图。路径权重是该路径中各条边权重的和。
- 17.两种遍历:①广度优先遍历[队列]:类似于树的层次遍历。②深度优先遍历[栈]:类似于树的前序遍历。(图中不存在根结点,所以可以从任一顶点开始)
- 18.测试连通性:不论哪个为起始顶点,当且仅当广度优先遍历中的顶点数目等于图中的顶点数目时,该图才是连通的。
- 19.最小生成树:含有图中所有顶点和部分边的树,其边的权重总和小于或等于同一个图中其他任何一棵生成树的权重总和。
- 20.判断最短路径:①在广度优先遍历期间在对每个顶点存储另两个信息即可:从起始顶点到本顶点的路径长度,以及路径中作为本顶点前驱的那个顶点。②寻找加权图的最便宜路径。
- 21.邻接列表:用一种类似于链表的动态结点来存储每个结点带有的边。
教材学习中的问题和解决过程
- 问题1:无向图中的连通和完全之间的关系是什么。
- 问题1解决方案:
| 区别 | 联系 | |
|---|---|---|
| 完全 | 任意两个顶点之间都会有一条边 | |
| 连通 | 任意两个顶点之间都存在一条路径 | 完全的一定连通 |
-
问题2:拓扑序的深入了解。
-
问题2解决方案:(1)每个顶点出现且只出现一次;(2)若A在序列中排在B的前面,则在图中不存在从B到A的路径。也可以定义为:拓扑排序是对有向无环图的顶点的一种排序,它使得如果存在一条从顶点A到顶点B的路径,那么在排序中B出现在A的后面。该排序算法将偏序关系转换为了全序关系,从而保证了结果的唯一性。
-
补充知识:偏序:有向图中两个顶点之间不存在环路,至于连通与否,是无所谓的。全序:就是在偏序的基础之上,有向无环图中的任意一对顶点还需要有明确的关系(反映在图中,就是单向连通的关系,注意不能双向连通,那就成环了)。
-
问题3:广度优先遍历的代码理解。
public Iterator<T> iteratorBFS(int startIndex)
{
Integer x;
QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();
UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();
if (!indexIsValid(startIndex))
return resultList.iterator();
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false;
traversalQueue.enqueue(new Integer(startIndex));
visited[startIndex] = true;
while (!traversalQueue.isEmpty())
{
x = traversalQueue.dequeue();
resultList.addToRear(vertices[x.intValue()]);
for (int i = 0; i < numVertices; i++)
{
if (adjMatrix[x.intValue()][i] && !visited[i])
{
traversalQueue.enqueue(new Integer(i));
visited[i] = true;
}
}
}
return new GraphIterator(resultList.iterator());
}
- 问题3解决方案:用队列管理遍历,用无序列表构造结果。放入无序列表的顺序是标记元素已读的顺序,入队的顺序与放入无序列表的顶点的相邻顶点是否已读有关系,若已读就不入队,进入下一步入无序列表。
//先把所有的顶点都标记成未访问的。
for (int i = 0; i < numVertices; i++)
visited[i] = false;
//把其实顶点入队,标记为已访问。
traversalQueue.enqueue(new Integer(startIndex));
visited[startIndex] = true;
//当队不为空的时候,x等于队首元素
while (!traversalQueue.isEmpty())
{
x = traversalQueue.dequeue();
//intValue()以 int 类型返回该 Integer 的值。把顶点对应的值放入无序列表中。
resultList.addToRear(vertices[x.intValue()]);
//小于顶点数做一个循环,邻接矩阵的出的那个元素
for (int i = 0; i < numVertices; i++)
{
//如果顶点到i存在边并且i没有被标记,则i入队,i被标记。
if (adjMatrix[x.intValue()][i] && !visited[i])
{
traversalQueue.enqueue(new Integer(i));
visited[i] = true;
}
}
}
return new GraphIterator(resultList.iterator());
- 问题4:mstNetwork()方法中
resultGraph.adjMatrix[i][j]=Double.POSITIVE_INFINITY是什么意思? - 问题4解决方案:保存double 类型的正无穷大值的常量。
代码调试中的问题和解决过程
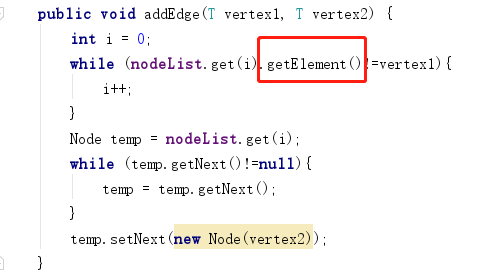
- 问题1:
- 问题1解决方案:改成下图就好,因为进行的是顶点的元素进行比较,而不是结点进行比较。
- 问题2:关于无向加权图的代码实现。
- 问题2解决方案:想法及理解在注释中体现。
//增加顶点
public void addVertex(T vertex) {
//越界扩容
if ((numVertices + 1) == adjMatrix.length)
expandCapacity();
//把新加顶点到剩下所有顶点的路径定义为正无穷(邻接矩阵)
vertices[numVertices] = vertex;
for (int i = 0; i <= numVertices; i++) {
adjMatrix[numVertices][i] = Double.POSITIVE_INFINITY;
adjMatrix[i][numVertices] = Double.POSITIVE_INFINITY;
}
numVertices++;
modCount++;
}
//删除顶点
public void removeVertex(T vertex) {
removeVertex(getIndex(vertex));
}
//根据索引去找到该顶点
public void removeVertex(int index) {
//当索引值存在时
if (indexIsValid(index)) {
//从该顶点开始,顶点集中的每个数的位置需要向前移一位
for (int j = index; j < numVertices - 1; j++) {
vertices[j] = vertices[j + 1];
}
//数组中的最后一个位置定义为空
vertices[numVertices - 1] = null;
//从该顶点开始,边的起点从该顶点变为下一个顶点,因为顶点集的位置向前移了一位。
for (int i = index; i < numVertices - 1; i++) {
for (int x = 0; x < numVertices; x++)
adjMatrix[i][x] = adjMatrix[i + 1][x];
}
//因为无向图,所以从该顶点开始,边的终点从该顶点变为下一个顶点依次类推
for (int i = index; i < numVertices; i++) {
for (int x = 0; x < numVertices; x++)
adjMatrix[x][i] = adjMatrix[x][i + 1];
}
//数组中最后一个位置为空,到各个顶点的边为空
for (int i = 0; i < numVertices; i++) {
adjMatrix[numVertices][i] = Double.POSITIVE_INFINITY;
adjMatrix[i][numVertices] = Double.POSITIVE_INFINITY;
}
//个数-1,操作次数+1
numVertices--;
modCount++;
}
}
//输入顶点添加边
public void addEdge(T vertex1, T vertex2, double weight) {
//根据顶点的索引值添加边
addEdge(getIndex(vertex1), getIndex(vertex2), weight);
}
public void addEdge(int index1, int index2, double weight) {
//当起点终点的索引值都存在的时候,因为是无向图,所以权重都相同,邻接矩阵相应的位置放入权重。操作次数+1
if (indexIsValid(index1) && indexIsValid(index2)) {
adjMatrix[index1][index2] = weight;
adjMatrix[index2][index1] = weight;
modCount++;
}
}
//删除边
public void removeEdge(T vertex1, T vertex2) {
//根据顶点的索引值删除边
removeEdge(getIndex(vertex1), getIndex(vertex2));
}
public void removeEdge(int index1, int index2) {
//当起点终点的索引值都存在的时候
if (indexIsValid(index1) && indexIsValid(index2)) {
//把边上的权重都变为正无穷大
adjMatrix[index1][index2] = Double.POSITIVE_INFINITY;
adjMatrix[index2][index1] = Double.POSITIVE_INFINITY;
modCount++;
}
}
- 最小路径的代码比较长,所以一个方法一个方法的分析。
- 下面这个方法输出的是最小路径的长度。
//找到两个顶点间的最短路径
public int shortestPathLength(T startVertex, T targetVertex) {
//根据索引值找到最短路径长度
return shortestPathLength(getIndex(startVertex), getIndex(targetVertex));
}
private int shortestPathLength(int startIndex, int targetIndex) {
int result = 0;
//如果起始索引值或者终止索引值不存在时,返回0
if (!indexIsValid(startIndex) || !indexIsValid(targetIndex))
return 0;
int index1;
//找到起点到终点最小路径的顶点的索引值
Iterator<Integer> it = iteratorShortestPathIndices(startIndex, targetIndex);
//如果没有下一个则为0,没路径
if (it.hasNext())
index1 = ((Integer) it.next()).intValue();
else
return 0;
//有下一个则+1,作为长度
while (it.hasNext()) {
result++;
it.next();
}
return result;
}
- 下面这个方法输出的是最小路径中的顶点元素。
//输出最小路径中的顶点
public Iterator iteratorShortestPath(T startVertex, T targetVertex) {
return iteratorShortestPath(getIndex(startVertex), getIndex(targetVertex));
}
public Iterator iteratorShortestPath(int startIndex, int targetIndex) {
List<T> resultList = new ArrayList<T>();
if (!indexIsValid(startIndex) || !indexIsValid(targetIndex))
return resultList.iterator();
//得到最小路径中的顶点索引值
Iterator<Integer> it = iteratorShortestPathIndices(startIndex, targetIndex);
//把对应的顶点添加到列表里
while (it.hasNext())
resultList.add(vertices[((Integer) it.next()).intValue()]);
return new GraphIterator(resultList.iterator());
}
- 下面这个方法是两个方法中的基础,找到最小路径的中顶点对应的元素值(包括顺序)
protected Iterator<Integer> iteratorShortestPathIndices(int startIndex, int targetIndex) {
int index = startIndex;
int[] pathLength = new int[numVertices];/*存路径的长度*/
int[] predecessor = new int[numVertices];/*前驱顶点*/
QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();/*索引值*/
UnorderedListADT<Integer> resultList = new ArrayUnorderedList<Integer>();/*顶点元素*/
/*如果索引值不存在或者起始终止索引值相等,返回无序列表中的顶点元素*/
if (!indexIsValid(startIndex) || !indexIsValid(targetIndex) || (startIndex == targetIndex))
return resultList.iterator();
/*做标记,先把标记数组全部变为false*/
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false;
/*把起始索引值加入列表*/
traversalQueue.enqueue(Integer.valueOf(startIndex));
/*对该索引值进行标记*/
visited[startIndex] = true;
/*该长度数组中该索引值的位置定位为0,前驱结点定义为-1*/
pathLength[startIndex] = 0;
predecessor[startIndex] = -1;
/*当索引值列表不为空并且起始和终止顶点元素不同时*/
while (!traversalQueue.isEmpty() && (index != targetIndex)) {
//index = 出队列的元素(也就是之前存入的索引值)
index = (traversalQueue.dequeue()).intValue();
//找出该索引值到每个顶点的边
for (int i = 0; i < numVertices; i++) {
//如果边存在,并且终点未标记(也就是这个边没有找到过)
if (adjMatrix[index][i] < Double.POSITIVE_INFINITY && !visited[i]) {
/*把边的终点的索引值对应的长度数组+1*/
pathLength[i] = pathLength[index] + 1;
/*前驱结点终点的索引值对应的位置存入index*/
predecessor[i] = index;
/*把新的索引值加入队列*/
traversalQueue.enqueue(Integer.valueOf(i));
/*标记该顶点*/
visited[i] = true;
}
}
}
if (index != targetIndex) // no path must have been found
return resultList.iterator();
StackADT<Integer> stack = new LinkedStack<Integer>();
index = targetIndex;
//找到最小路径中的顶点索引值,进行入栈
stack.push(Integer.valueOf(index));
do {
index = predecessor[index];
stack.push(Integer.valueOf(index));
} while (index != startIndex);
//依次弹栈得到正确的顺序
while (!stack.isEmpty())
resultList.addToRear((stack.pop()));
return new NetworkIndexIterator(resultList.iterator());
}
- 作为无向加权图的重要方法(最特殊的),因为有权重,所以存在一个找最便宜的方法
//找到最便宜的路
public double shortestPathWeight(T vertex1, T vertex2) {
return shortestPathWeight(getIndex(vertex1), getIndex(vertex2));
}
public double shortestPathWeight(int start, int end) {
Double[] dist = new Double[numVertices];//存放该顶点对所有有边顶点的权重
boolean[] flag = new boolean[numVertices];//标记结点
for (int i = 0; i < numVertices; i++) {
flag[i] = false;/*让所有都变成未标记*/
dist[i] = adjMatrix[start][i];/*初始等于该顶点到所有顶点的权重(包括不存在边的为正无穷)*/
}
flag[start] = true;/*把开始顶点标记*/
int k = 0;
for (int i = 0; i < numVertices; i++) {
Double min = Double.POSITIVE_INFINITY;
for (int j = 0; j < numVertices; j++) {
//如果为标记,并且该索引值下存在权重(也就是存在边)
if (flag[j] == false && dist[j] < min && dist[j] != -1 && dist[j] != 0) {
min = dist[j];/*最小值就为该权重*/
k = j;/*让k等于该索引值*/
}
}
flag[k] = true;/*标记该索引值的顶点*/
/*找k索引值的剩下权重是否存在,如果有找到最小的添加到min里,如果没有一直+0*/
for (int j = 0; j < numVertices; j++) {
if (adjMatrix[k][j] != -1&&dist[j]!= -1) {
double temp = (adjMatrix[k][j] == Double.POSITIVE_INFINITY ? Double.POSITIVE_INFINITY : (min + adjMatrix[k][j]));
//如果j未标记并且temp小于权重组中原有值,则让权重组j为索引的位置为temp
if (flag[j] == false && (temp < dist[j])) {
dist[j] = temp;
}
}
}
}
return dist[end];
}
代码托管
24540
上周考试错题总结
点评过的同学博客和代码
其他(感悟、思考等,可选)
- 图可谓是学了两个学期java碰见的最难的东西了/微笑,并不是概念难而是绕着绕着就把自己老绕晕了,还有就是可能理解了原理,但是代码并不知道怎么实现。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 2/2 | |
| 第二周 | 1010/1010 | 1/2 | 10/12 | |
| 第三周 | 651/1661 | 1/3 | 13/25 | |
| 第四周 | 2205/3866 | 1/4 | 15/40 | |
| 第五周 | 967/4833 | 2/6 | 22/62 | |
| 第六周 | 1680/6513 | 1/7 | 34/96 | |
| 第七周 | 2196/8709 | 1/8 | 35/131 | |
| 第八周 | 1952/10661 | 2/9 | 49/180 | |
| 第九周 | 2100/24540 | 1/10 | 40/131 |
-
计划学习时间:30小时
-
实际学习时间:40小时
-
改进情况:图的概念很好理解,但是实现很难!






 浙公网安备 33010602011771号
浙公网安备 33010602011771号