20172332 2017-2018-2 《程序设计与数据结构》实验三报告
20172332 2017-2018-2 《程序设计与数据结构》实验三报告
课程:《程序设计与数据结构》
班级: 1723
姓名: 于欣月
学号:20172332
实验教师:王志强
实验日期:2018年11月20日
必修/选修: 必修
1.实验内容
- 查找与排序-1
- 定义一个Searching和Sorting类,并在类中实现linearSearch(教材P162 ),SelectionSort方法(P169),最后完成测试。
要求不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位
提交运行结果图。 - 查找与排序-2
- 重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1723.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1723.G2301)
把测试代码放test包中
重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种) - 查找与排序-3
- 参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试
提交运行结果截图 - 查找与排序-4
- 补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个)
测试实现的算法(正常,异常,边界)
提交运行结果截图
(3分,如果编写多个排序算法,即使其中三个排序程序有瑕疵,也可以酌情得满分) - 查找与排序-5(选做,加分)
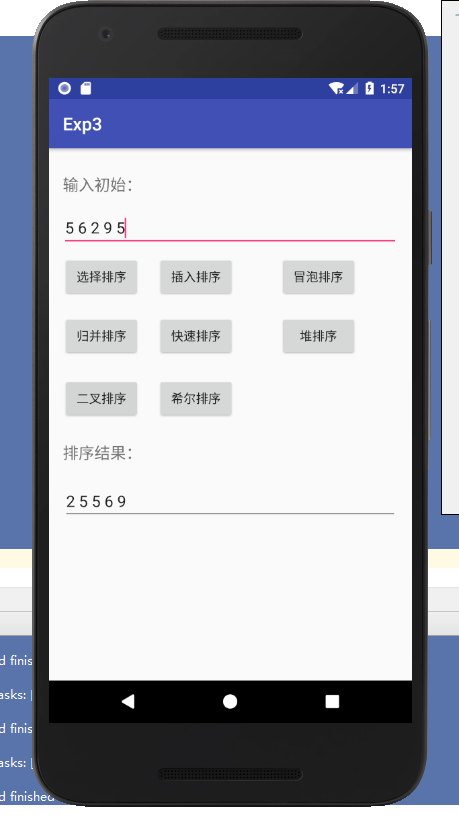
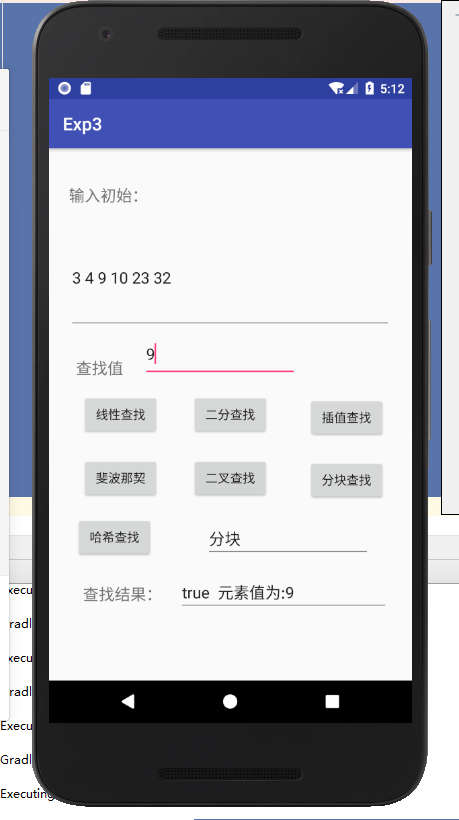
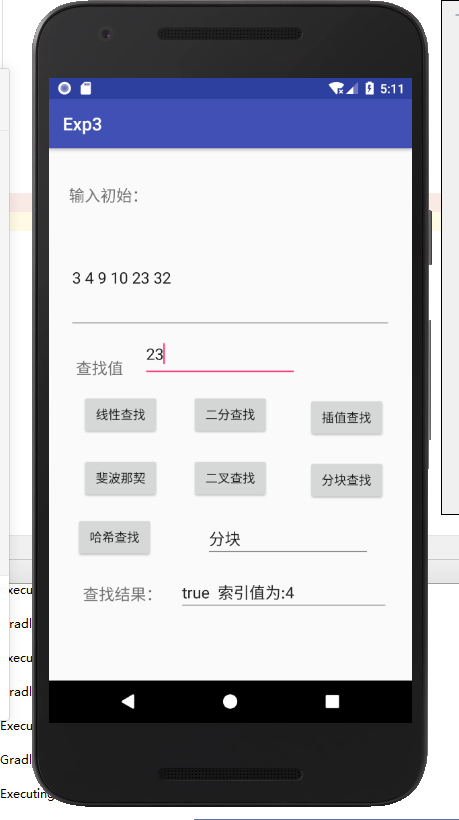
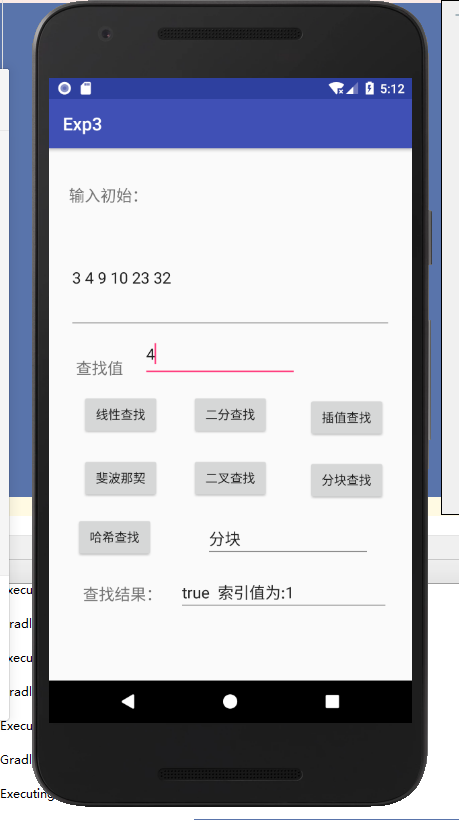
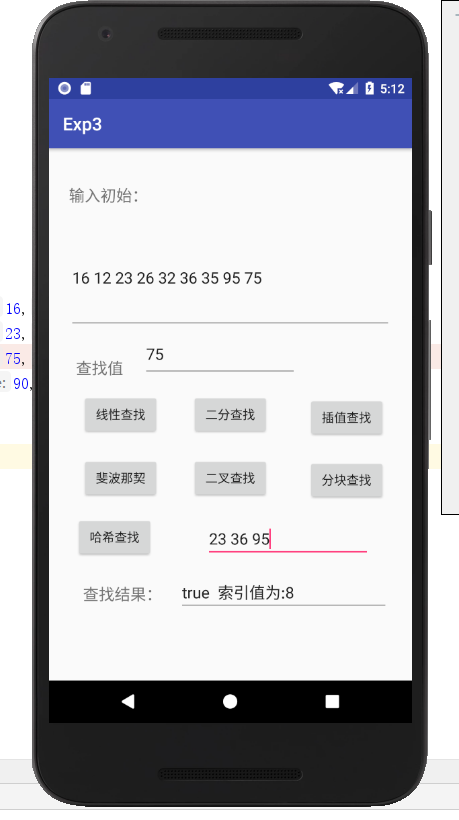
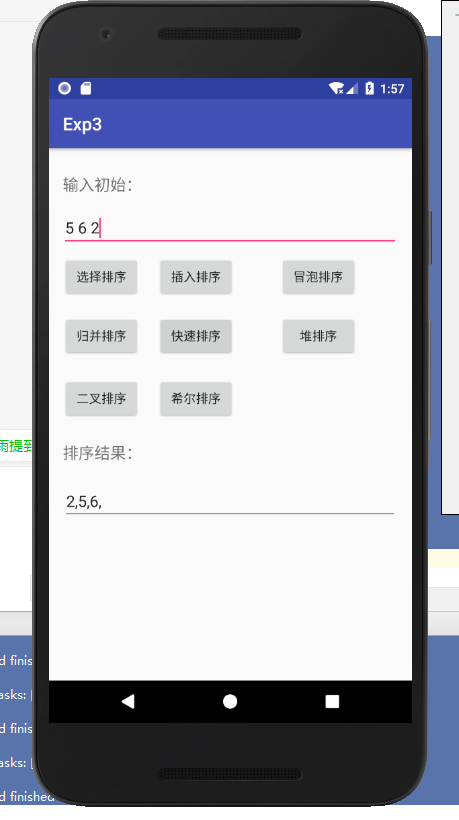
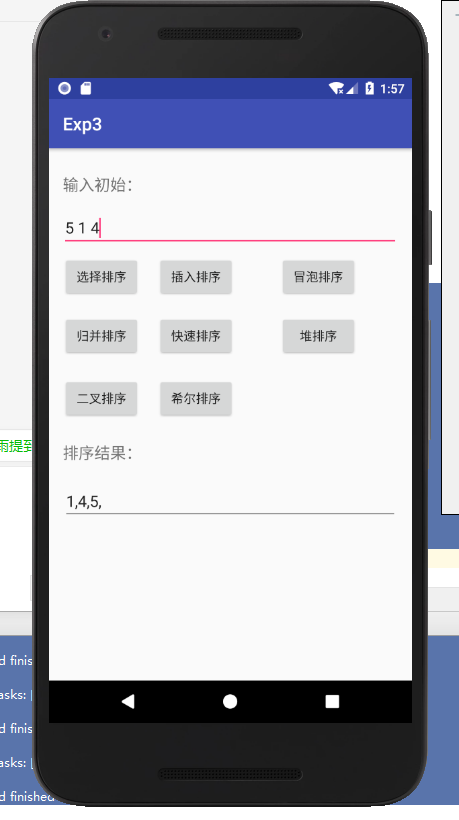
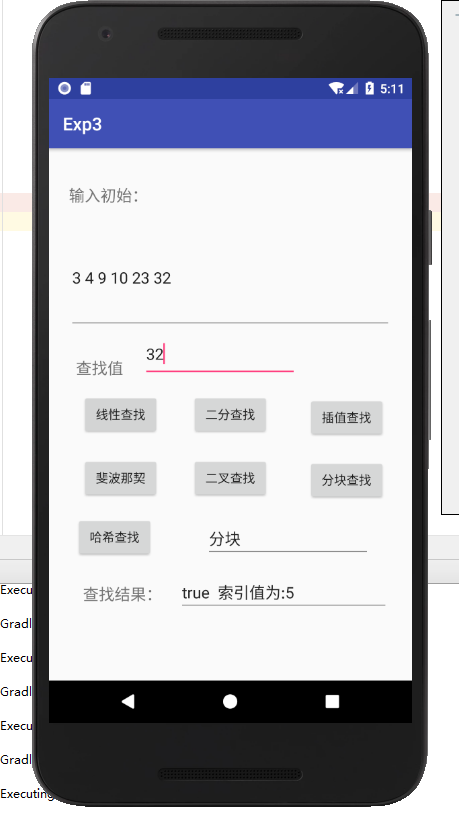
- 编写Android程序对各种查找与排序算法进行测试
提交运行结果截图
推送代码到码云
(加分3,加到实验中)
2. 实验过程及结果
前期准备:
- 1.了解多种查找方法与排序方法的原理及实现
过程:
- 1.实验一
- 关键代码:
public static <T> boolean linearSearch(T[] data, int min, int max, T target) {
int index = min;
boolean found = false;
while (!found && index <= max) {
found = data[index].equals(target);
index++;
}
return found;
}
//线性查找
public static <T> boolean linearSearch(T[] data, int min, int max, T target) {
int index = min;
boolean found = false;
while (!found && index <= max) {
found = data[index].equals(target);
index++;
}
return found;
}
//选择排序
public static <T extends Comparable<T>>
String selectionSort(T[] data)
{
int min;
T temp;
for (int index = 0; index < data.length-1; index++)
{
min = index;
for (int scan = index+1; scan < data.length; scan++)
if (data[scan].compareTo(data[min])<0)
min = scan;
swap(data, min, index);
}
String res = "";
for(int i = 0;i<data.length;i++)
res += data[i]+",";
return res;
}
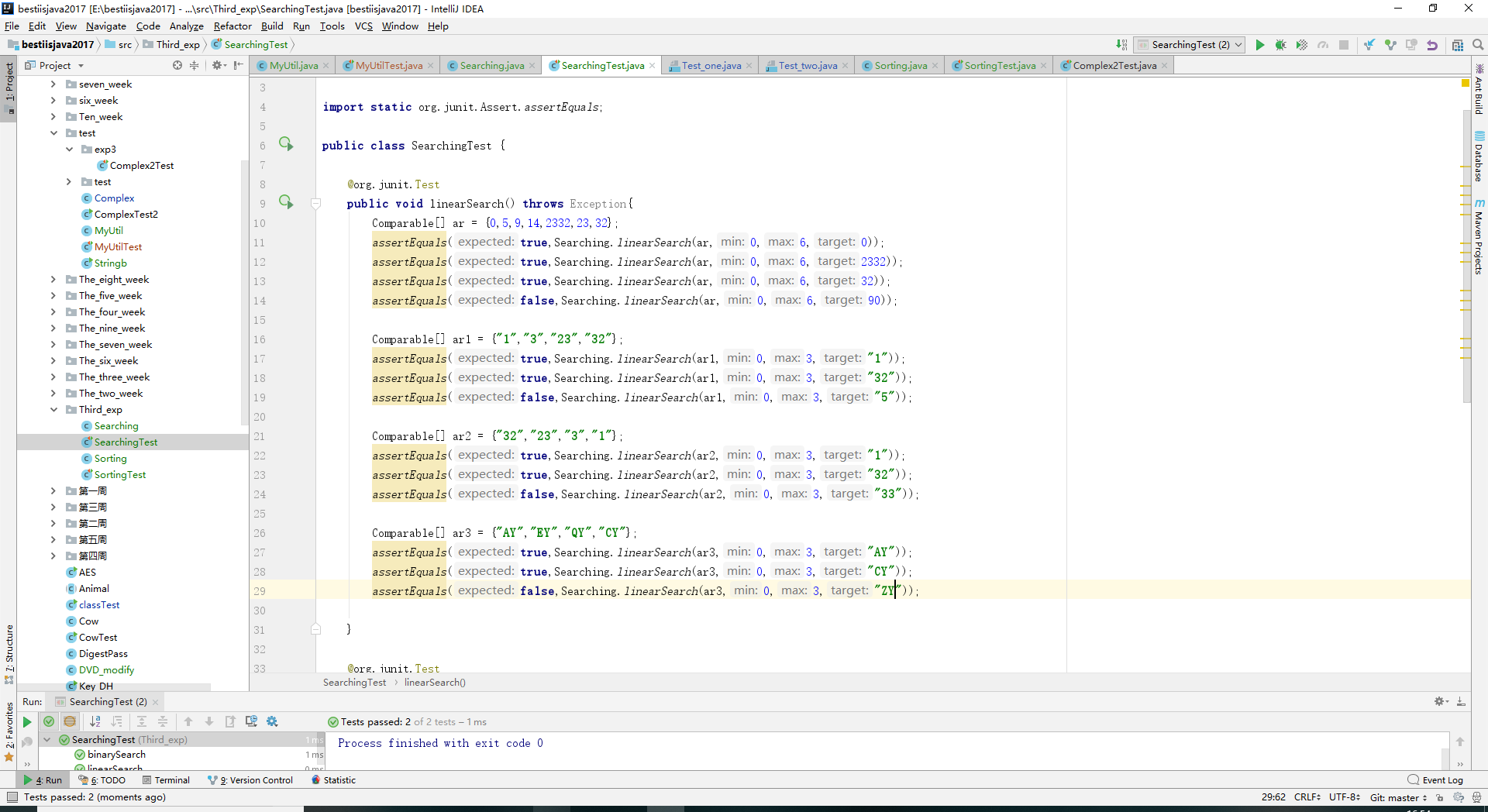
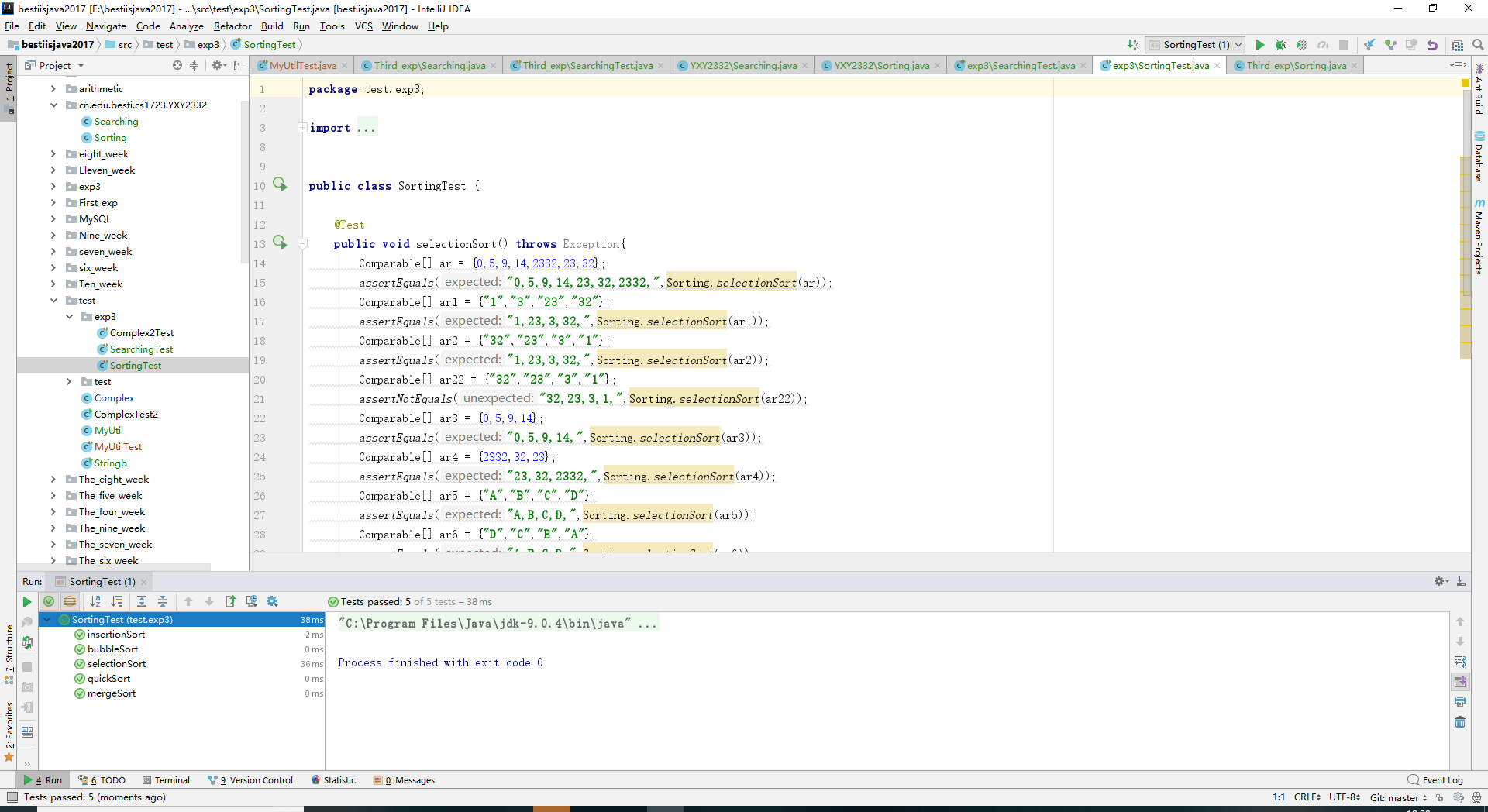
- 实验结果:
- 2.实验二
- 关键代码:
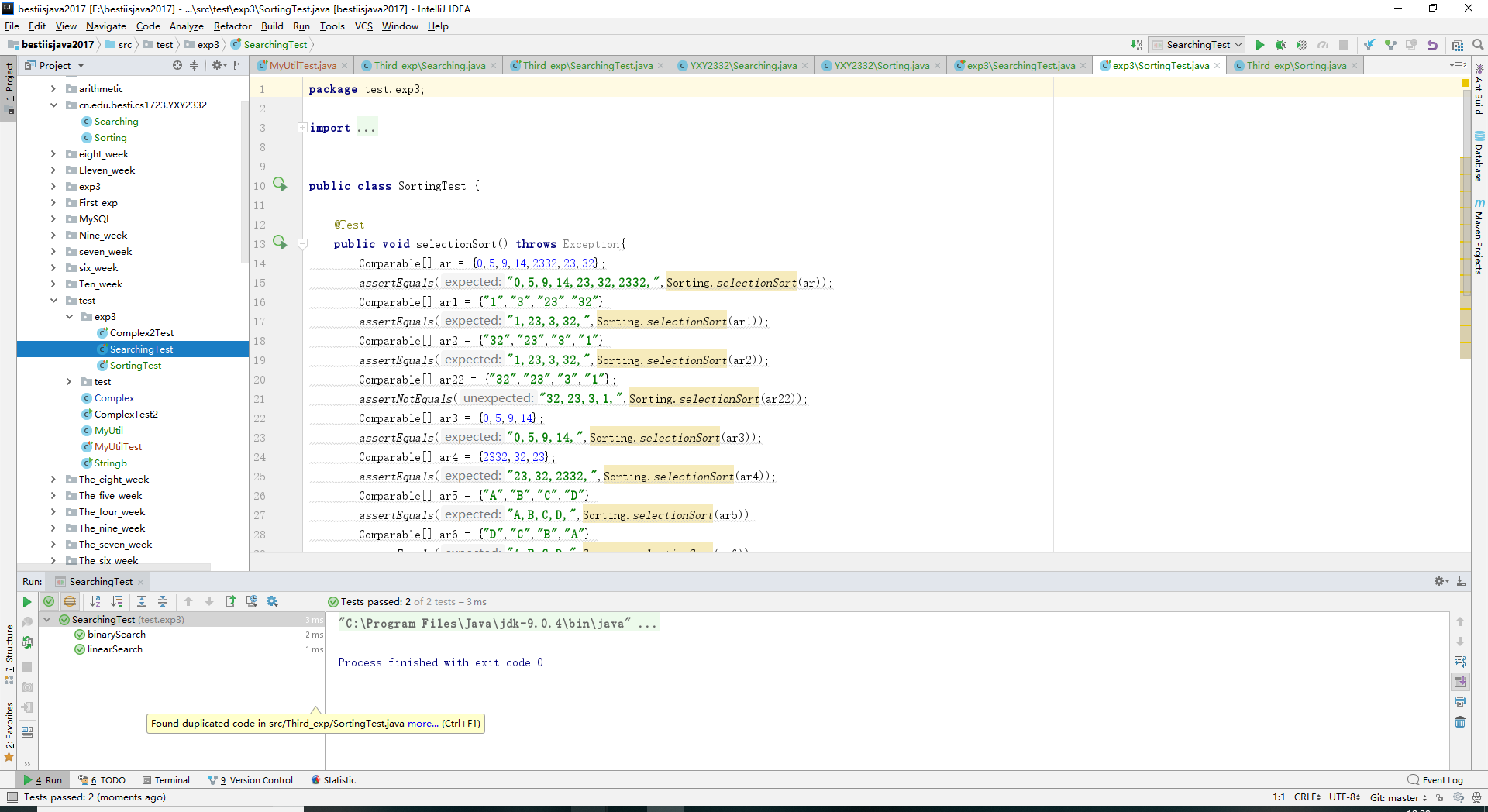
与实验一相同。 - 实验结果:
- 关键代码:
- 3.实验三
- 关键代码:
/**
* Searches the specified array of objects using a binary search
* algorithm.
*
* @param data the array to be searched
* @param min the integer representation of the minimum value
* @param max the integer representation of the maximum value
* @param target the element being searched for
* @return true if the desired element is found
*/
//二分查找
public static <T extends Comparable<T>> boolean binarySearch(T[] data, int min, int max, T target) {
boolean found = false;
int midpoint = (min + max) / 2; // determine the midpoint
if (data[midpoint].compareTo(target) == 0)
found = true;
else if (data[midpoint].compareTo(target) > 0) {
if (min <= midpoint - 1)
found = binarySearch(data, min, midpoint - 1, target);
} else if (midpoint + 1 <= max)
found = binarySearch(data, midpoint + 1, max, target);
return found;
}
//顺序查找
public static int SequenceSearch(int a[], int value, int n) {
int i;
for (i = 0; i < n; i++)
if (a[i] == value)
return i;
return -1;
}
//二分查找两个版本
public static int BinarySearch1(int a[], int value, int n) {
int low, high, mid;
low = 0;
high = n - 1;
while (low <= high) {
mid = (low + high) / 2;
if (a[mid] == value)
return mid;
if (a[mid] > value)
high = mid - 1;
if (a[mid] < value)
low = mid + 1;
}
return -1;
}
//二分查找,递归版本
public static int BinarySearch2(int a[], int value, int low, int high) {
if (high < low)
return -1;
int mid = low + (high - low) / 2;
if (a[mid] == value)
return mid;
else if (a[mid] > value)
return BinarySearch2(a, value, low, mid - 1);
else if (a[mid] < value)
return BinarySearch2(a, value, mid + 1, high);
else
return -1;
}
//插值查找
public static int InsertionSearch(int[] data, int target, int min, int max) {
if (min == max)
return -1;
int mid = min + (target - data[min]) / (data[max] - data[min]) * (max - min);
if (data[mid] == target)
return mid;
else if (data[mid] > target)
return InsertionSearch(data, target, min, mid - 1);
else if (data[mid] < target)
return InsertionSearch(data, target, mid + 1, max);
else
return -1;
}
//斐波那契查找
private static int[] fibonacci() {
int[] f = new int[10];
f[0] = 0;
f[1] = 1;
for (int i = 2; i < f.length; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
public static int fibonacciSearch(int[] data, int key) {
int low = 0;
int high = data.length - 1;
int mid = 0;
// 斐波那契分割数值下标
int k = 0;
// 序列元素个数
int i = 0;
// 获取斐波那契数列
int[] f = fibonacci();
// 获取斐波那契分割数值下标
while (data.length > f[k] - 1) {
k++;
}
// 创建临时数组
int[] temp = new int[f[k] - 1];
for (int j = 0; j < data.length; j++)
temp[j] = data[j];
// 序列补充至f[k]个元素
// 补充的元素值为最后一个元素的值
for (i = data.length; i < f[k] - 1; i++) {
temp[i] = temp[high];
}
while (low <= high) {
// low:起始位置
// 前半部分有f[k-1]个元素,由于下标从0开始
// 则-1 获取 黄金分割位置元素的下标
mid = low + f[k - 1] - 1;
if (temp[mid] > key) {
// 查找前半部分,高位指针移动
// (全部元素) = (前半部分)+(后半部分)
// f[k] = f[k-1] + f[k-1]
// 因为前半部分有f[k-1]个元素,所以 k = k-1
high = mid - 1;
k = k - 1;
} else if (temp[mid] < key) {
// 查找后半部分,高位指针移动
// (全部元素) = (前半部分)+(后半部分)
// f[k] = f[k-1] + f[k-1]
// 因为后半部分有f[k-1]个元素,所以 k = k-2
low = mid + 1;
k = k - 2;
} else {
// 如果为真则找到相应的位置
if (mid <= high) {
return mid;
} else {
// 出现这种情况是查找到补充的元素
// 而补充的元素与high位置的元素一样
return high;
}
}
}
return -1;
}
public static int treeSearch(int[] arr, int key) {
LinkedBinarySearchTree tree = new LinkedBinarySearchTree();
for (int a = 0; a < arr.length; a++) {
tree.addElement(arr[a]);
}
if (tree.find(key) != null)
return (int) tree.find(key);
else
throw new ElementNotFoundException();
}
//分块查找
//index代表索引数组,st2代表待查找数组,keytype代表要查找的元素,m代表每块大小
public static int blocksearch(int[] index, int[] st2, int keytype, int m) {
int i = linearSearch(index, 0, st2.length - 1, keytype); //shunxunsearch函数返回值为带查找元素在第几块
if (i >= 0) {
int j = m * i; //j为第i块的第一个元素下标
int curlen = (i + 1) * m;
while (j < curlen) {
if (st2[j] == keytype)
return j;
j++;
}
}
return -1;
}
public static <T> int linearSearch(int[] data, int min, int max, int target) {
int index = min;
if (data[index] >= target)
return 0;
int i=1;
while(i<data.length) {
if((data[i-1]<target)&&(data[i]>target))
return i;
else
i++;
}
return -1;
}
//哈希查找
public static int hashSearch(int data[], int target) {
HashMap<Integer, Integer> hashMap = new HashMap<>();
for (int i = 0; i < data.length; i++)
hashMap.put(Integer.hashCode(data[i]), data[i]);
int key = Integer.hashCode(target);
if (hashMap.containsKey(key))
return hashMap.get(key);
return -1;//找不到返回-1
}
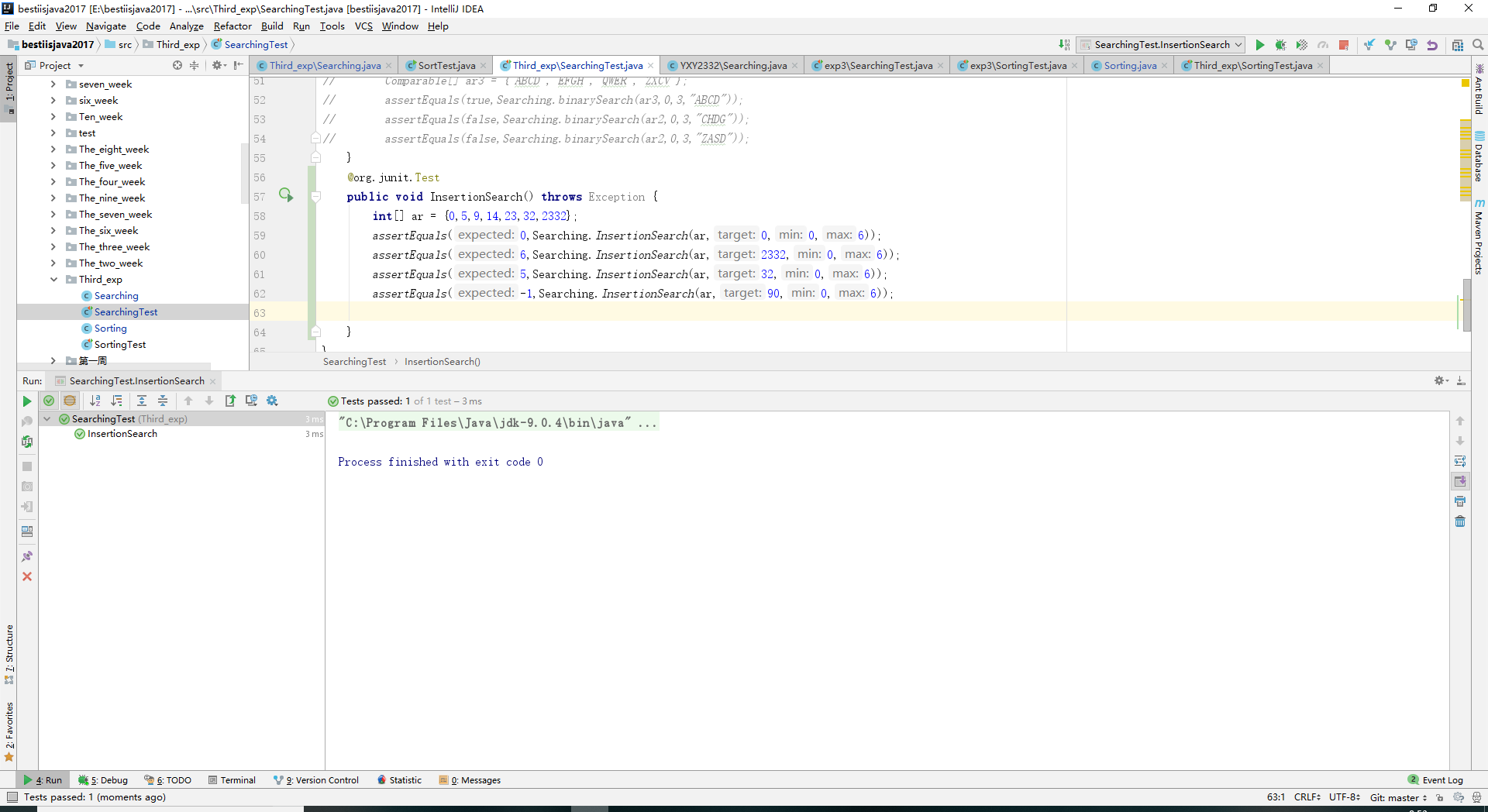
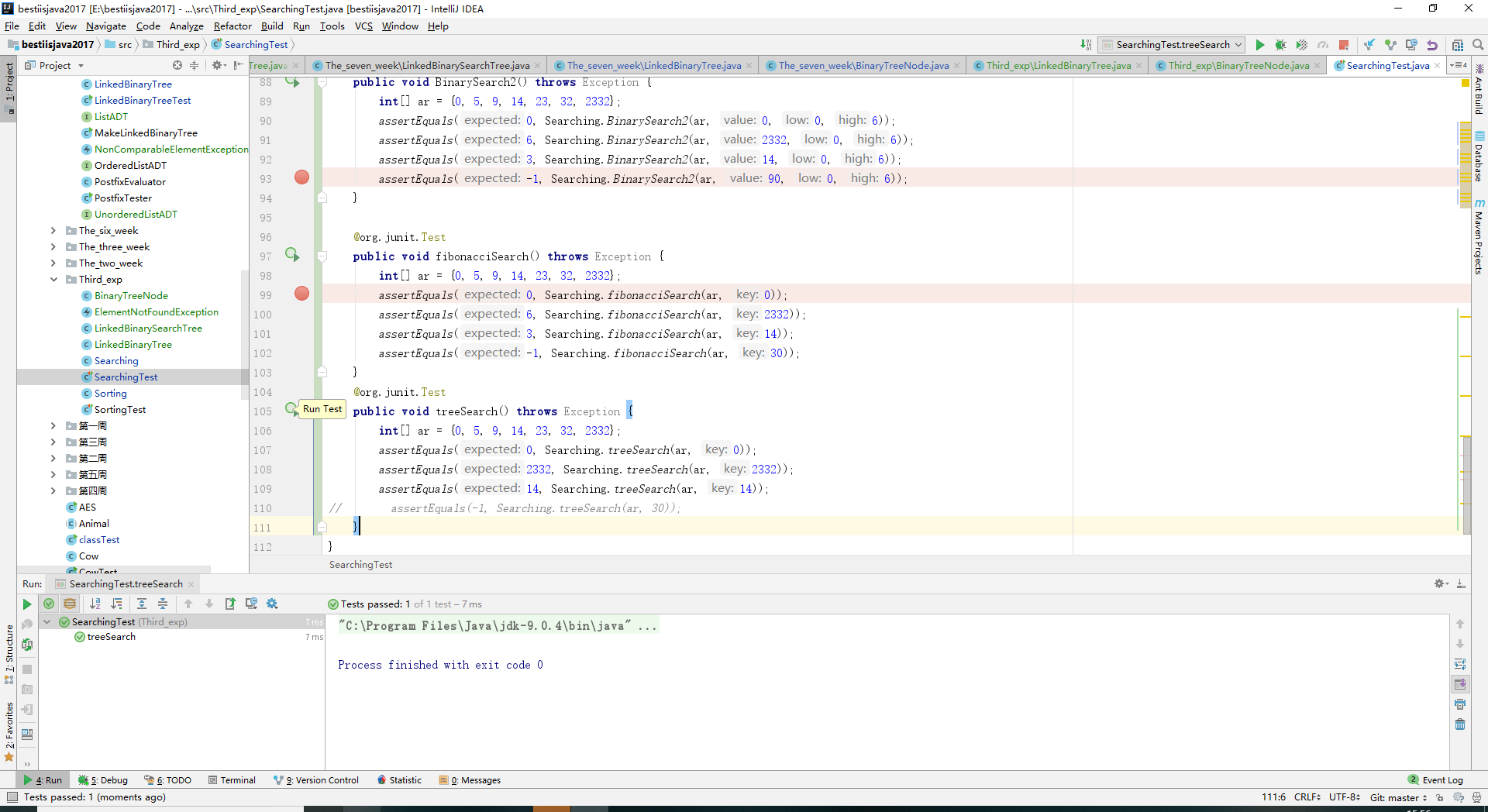
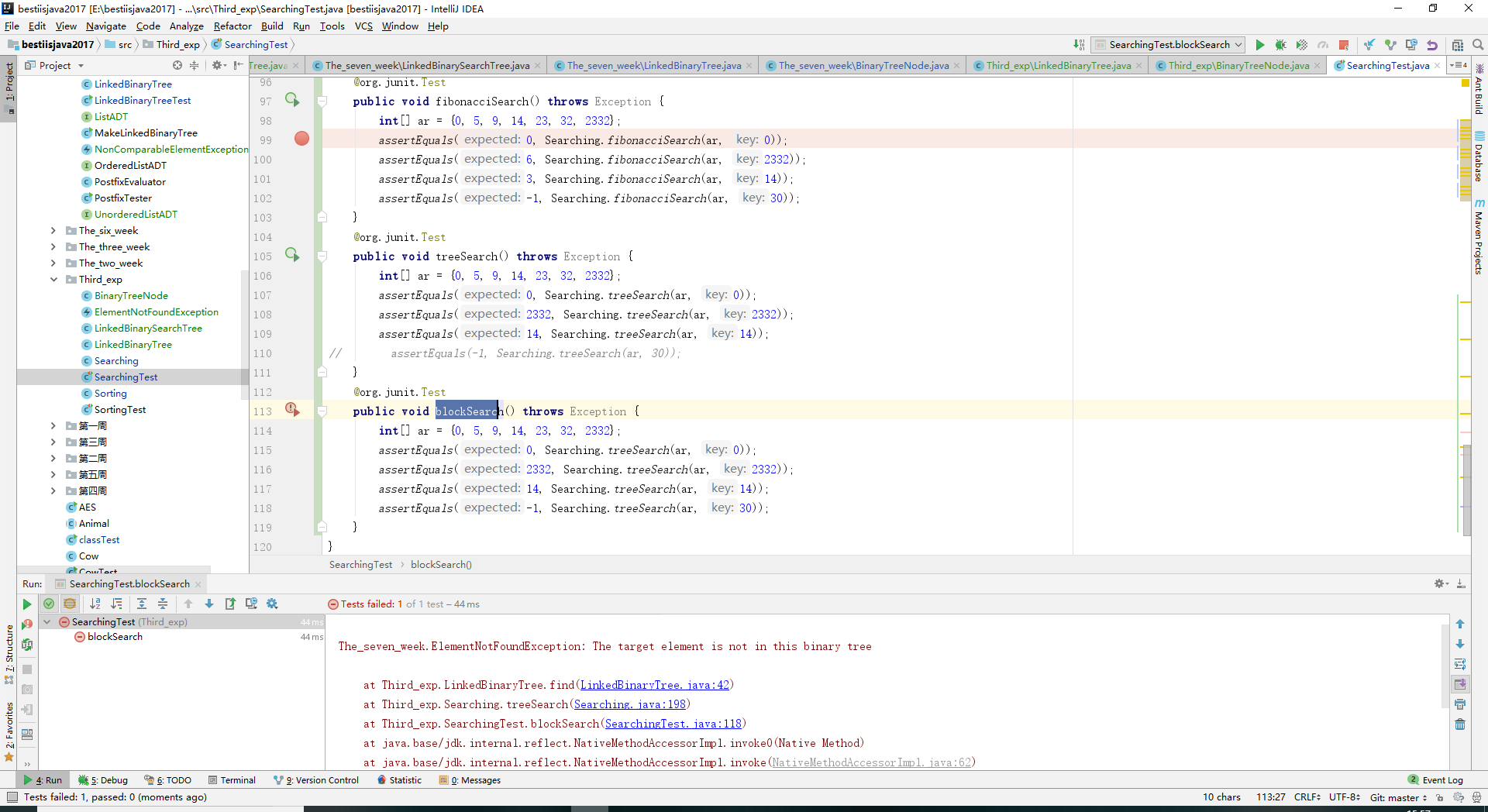
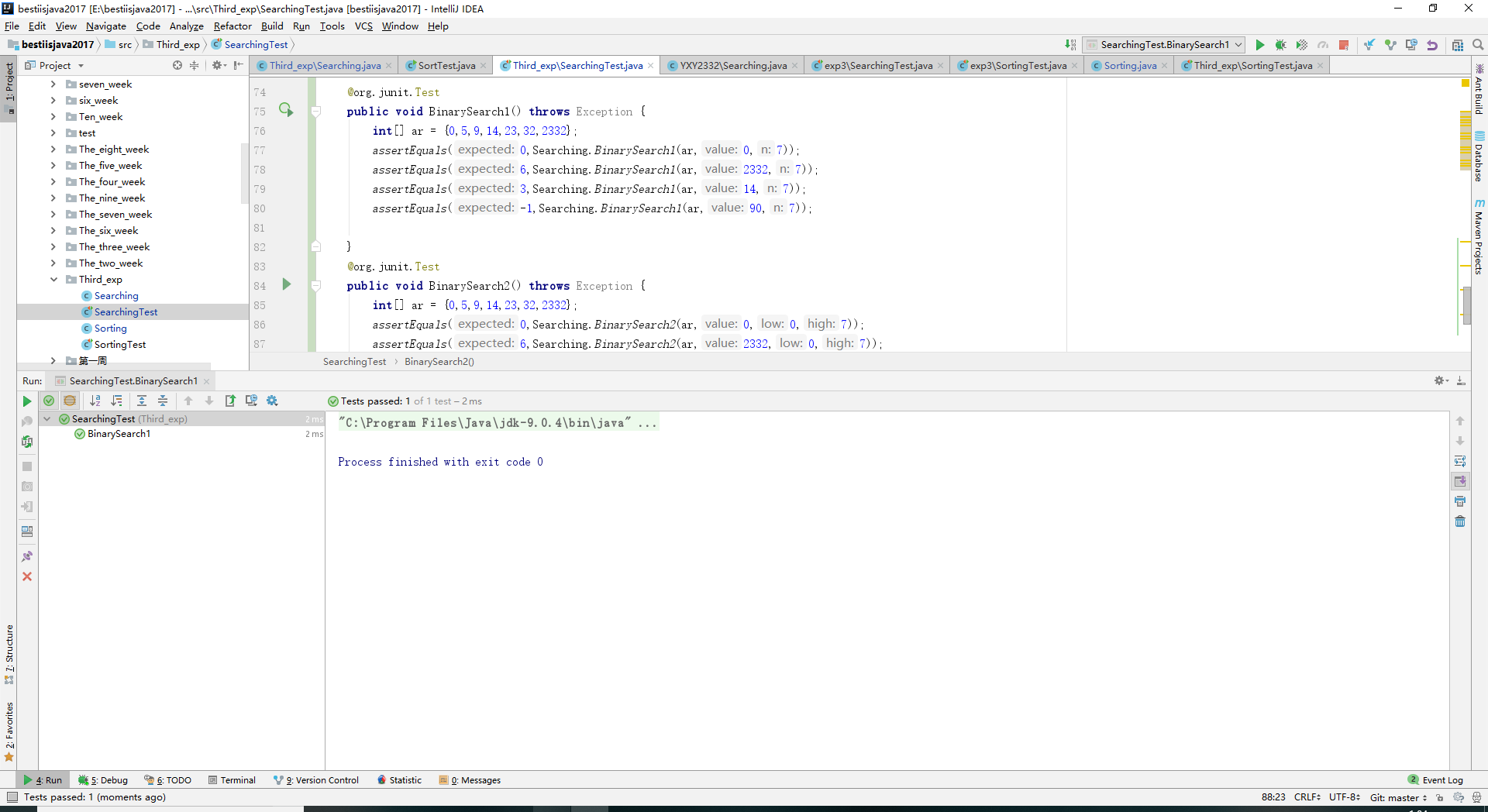
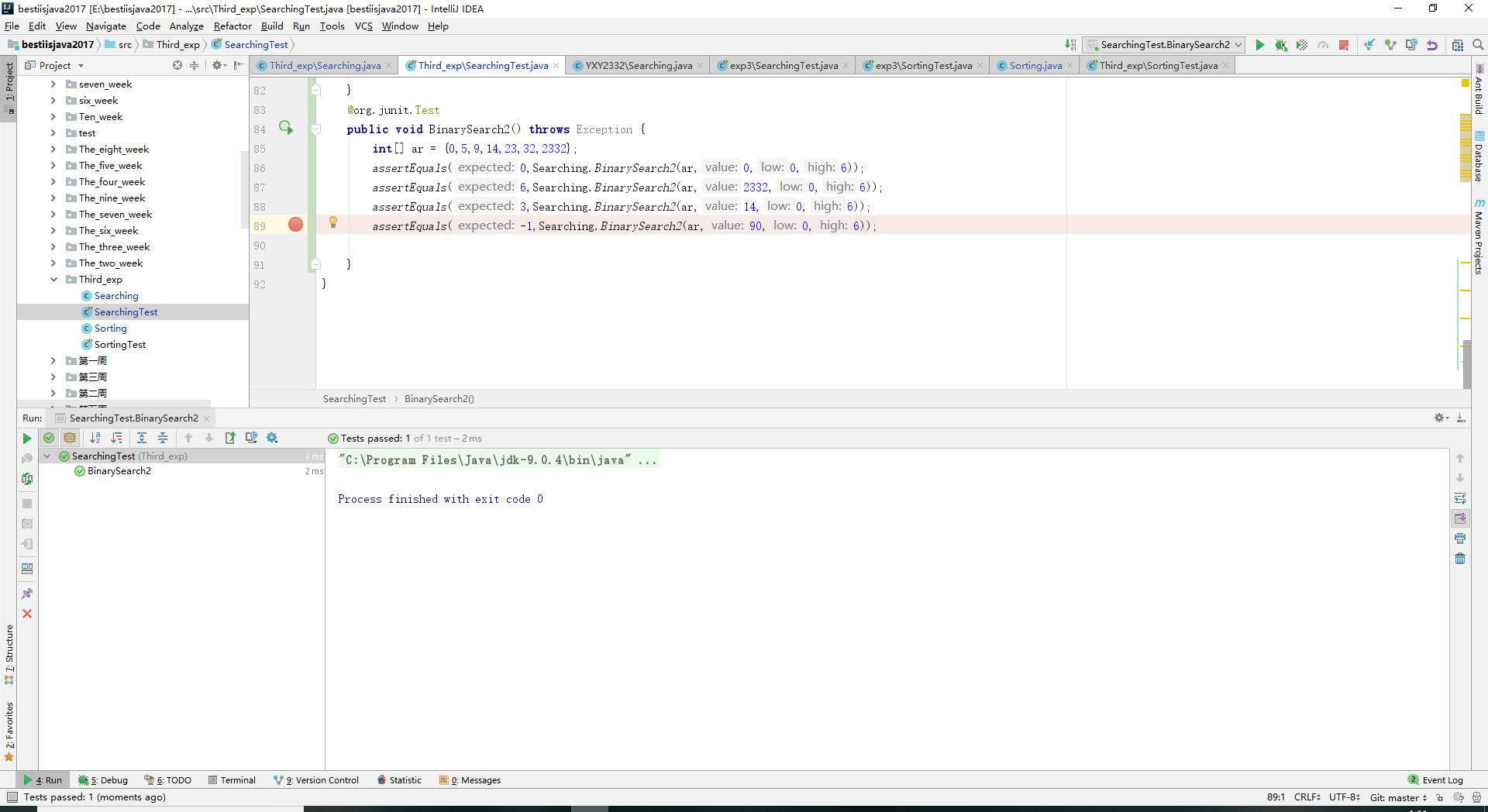
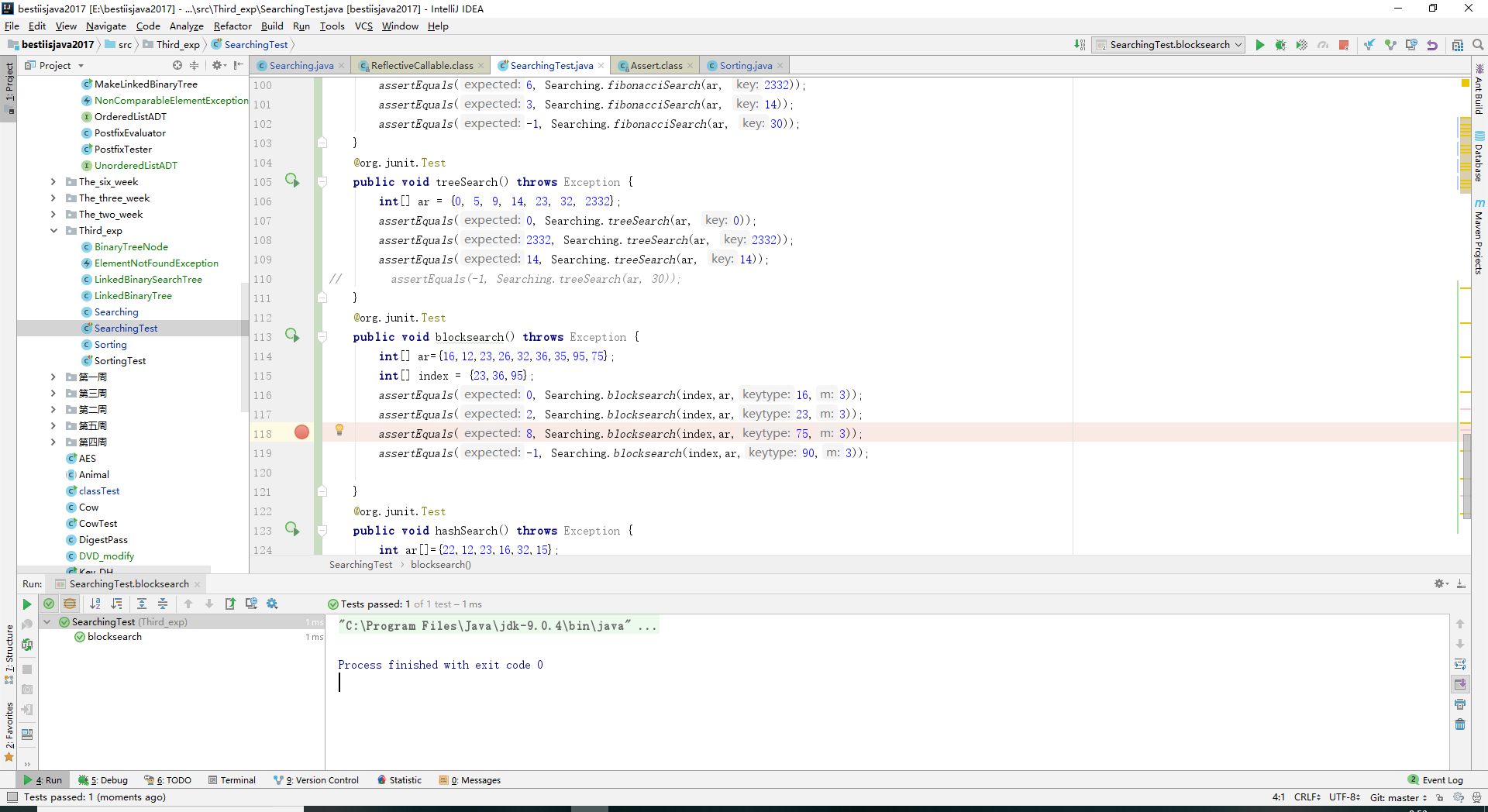
- 实验结果:
- 实验四
- 关键代码:
public static <T extends Comparable<T>>
String selectionSort(T[] data)
{
int min;
T temp;
for (int index = 0; index < data.length-1; index++)
{
min = index;
for (int scan = index+1; scan < data.length; scan++)
if (data[scan].compareTo(data[min])<0)
min = scan;
swap(data, min, index);
}
String res = "";
for(int i = 0;i<data.length;i++)
res += data[i]+",";
return res;
}
/**
* Swaps to elements in an array. Used by various sorting algorithms.
*
* @param data the array in which the elements are swapped
* @param index1 the index of the first element to be swapped
* @param index2 the index of the second element to be swapped
*/
private static <T extends Comparable<T>> void swap(T[] data, int index1, int index2)
{
T temp = data[index1];
data[index1] = data[index2];
data[index2] = temp;
}
/**
* Sorts the specified array of objects using an insertion
* sort algorithm.
*
* @param data the array to be sorted
*/
public static <T extends Comparable<T>> void insertionSort(T[] data)
{
for (int index = 1; index < data.length; index++)
{
T key = data[index];
int position = index;
// shift larger values to the right
while (position > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1];
position--;
}
data[position] = key;
}
}
/**
* Sorts the specified array of objects using a bubble sort
* algorithm.
*
* @param data the array to be sorted
*/
public static <T extends Comparable<T>> void bubbleSort(T[] data)
{
int position, scan;
T temp;
for (position = data.length - 1; position >= 0; position--)
{
for (scan = 0; scan <= position - 1; scan++)
{
if (data[scan].compareTo(data[scan+1]) > 0)
swap(data, scan, scan + 1);
}
}
}
/**
* Sorts the specified array of objects using the merge sort
* algorithm.
*
* @param data the array to be sorted
*/
public static <T extends Comparable<T>> void mergeSort(T[] data)
{
mergeSort(data, 0, data.length - 1);
}
/**
* Recursively sorts a range of objects in the specified array using the
* merge sort algorithm.
*
* @param data the array to be sorted
* @param min the index of the first element
* @param max the index of the last element
*/
private static <T extends Comparable<T>> void mergeSort(T[] data, int min, int max)
{
if (min < max)
{
int mid = (min + max) / 2;
mergeSort(data, min, mid);
mergeSort(data, mid+1, max);
merge(data, min, mid, max);
}
}
/**
* Merges two sorted subarrays of the specified array.
*
* @param data the array to be sorted
* @param first the beginning index of the first subarray
* @param mid the ending index fo the first subarray
* @param last the ending index of the second subarray
*/
@SuppressWarnings("unchecked")
private static <T extends Comparable<T>> void merge(T[] data, int first, int mid, int last)
{
T[] temp = (T[])(new Comparable[data.length]);
int first1 = first, last1 = mid; // endpoints of first subarray
int first2 = mid+1, last2 = last; // endpoints of second subarray
int index = first1; // next index open in temp array
// Copy smaller item from each subarray into temp until one
// of the subarrays is exhausted
while (first1 <= last1 && first2 <= last2)
{
if (data[first1].compareTo(data[first2]) < 0)
{
temp[index] = data[first1];
first1++;
}
else
{
temp[index] = data[first2];
first2++;
}
index++;
}
// Copy remaining elements from first subarray, if any
while (first1 <= last1)
{
temp[index] = data[first1];
first1++;
index++;
}
// Copy remaining elements from second subarray, if any
while (first2 <= last2)
{
temp[index] = data[first2];
first2++;
index++;
}
// Copy merged data into original array
for (index = first; index <= last; index++)
data[index] = temp[index];
}
/**
* Sorts the specified array of objects using the quick sort algorithm.
*
* @param data the array to be sorted
*/
public static <T extends Comparable<T>> void quickSort(T[] data)
{
quickSort(data, 0, data.length - 1);
}
/**
* Recursively sorts a range of objects in the specified array using the
* quick sort algorithm.
*
* @param data the array to be sorted
* @param min the minimum index in the range to be sorted
* @param max the maximum index in the range to be sorted
*/
private static <T extends Comparable<T>> void quickSort(T[] data, int min, int max)
{
if (min < max)
{
// create partitions
int indexofpartition = partition(data, min, max);
// sort the left partition (lower values)
quickSort(data, min, indexofpartition - 1);
// sort the right partition (higher values)
quickSort(data, indexofpartition + 1, max);
}
}
/**
* Used by the quick sort algorithm to find the partition.
*
* @param data the array to be sorted
* @param min the minimum index in the range to be sorted
* @param max the maximum index in the range to be sorted
*/
private static <T extends Comparable<T>> int partition(T[] data, int min, int max)
{
T partitionelement;
int left, right;
int middle = (min + max) / 2;
// use the middle data value as the partition element
partitionelement = data[middle];
// move it out of the way for now
swap(data, middle, min);
left = min;
right = max;
while (left < right)
{
// search for an element that is > the partition element
while (left < right && data[left].compareTo(partitionelement) <= 0)
left++;
// search for an element that is < the partition element
while (data[right].compareTo(partitionelement) > 0)
right--;
// swap the elements
if (left < right)
swap(data, left, right);
}
// move the partition element into place
swap(data, min, right);
return right;
}
public static String Xiersort(int[] arrays){
String res = "";
if(arrays == null || arrays.length <= 1){
return null;
}
//增量
int incrementNum = arrays.length/2;
while(incrementNum >=1){
for(int i=0;i<arrays.length;i++){
//进行插入排序
for(int j=i;j<arrays.length-incrementNum;j=j+incrementNum){
if(arrays[j]>arrays[j+incrementNum]){
int temple = arrays[j];
arrays[j] = arrays[j+incrementNum];
arrays[j+incrementNum] = temple;
}
}
}
//设置新的增量
incrementNum = incrementNum/2;
}
for (int i = 0;i<arrays.length;i++)
res+=arrays[i]+" ";
return res;
}
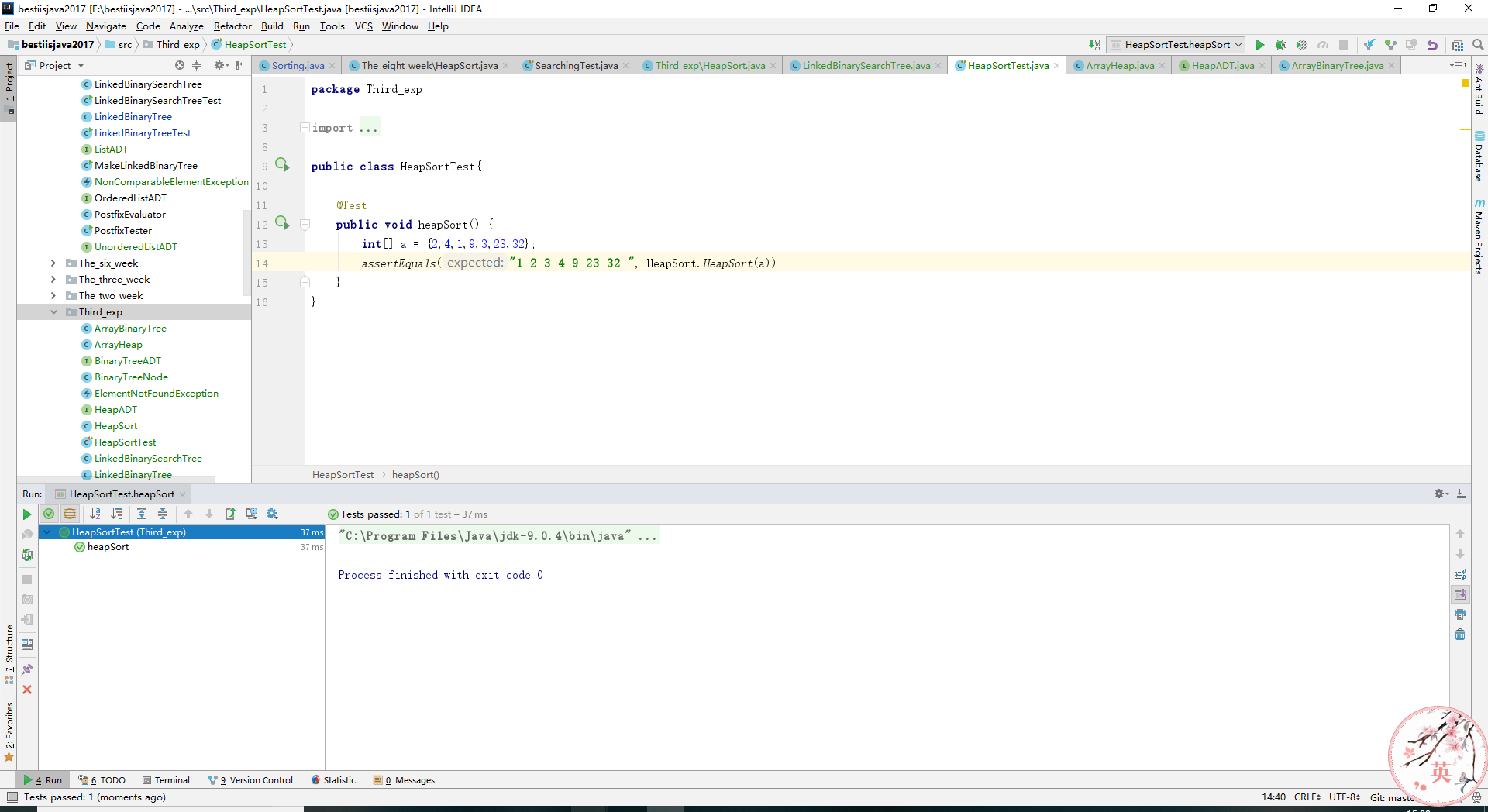
public void heapSort() {
int[] a = {2,4,1,9,3,23,32};
assertEquals("1 2 3 4 9 23 32 ", HeapSort.HeapSort(a));
}
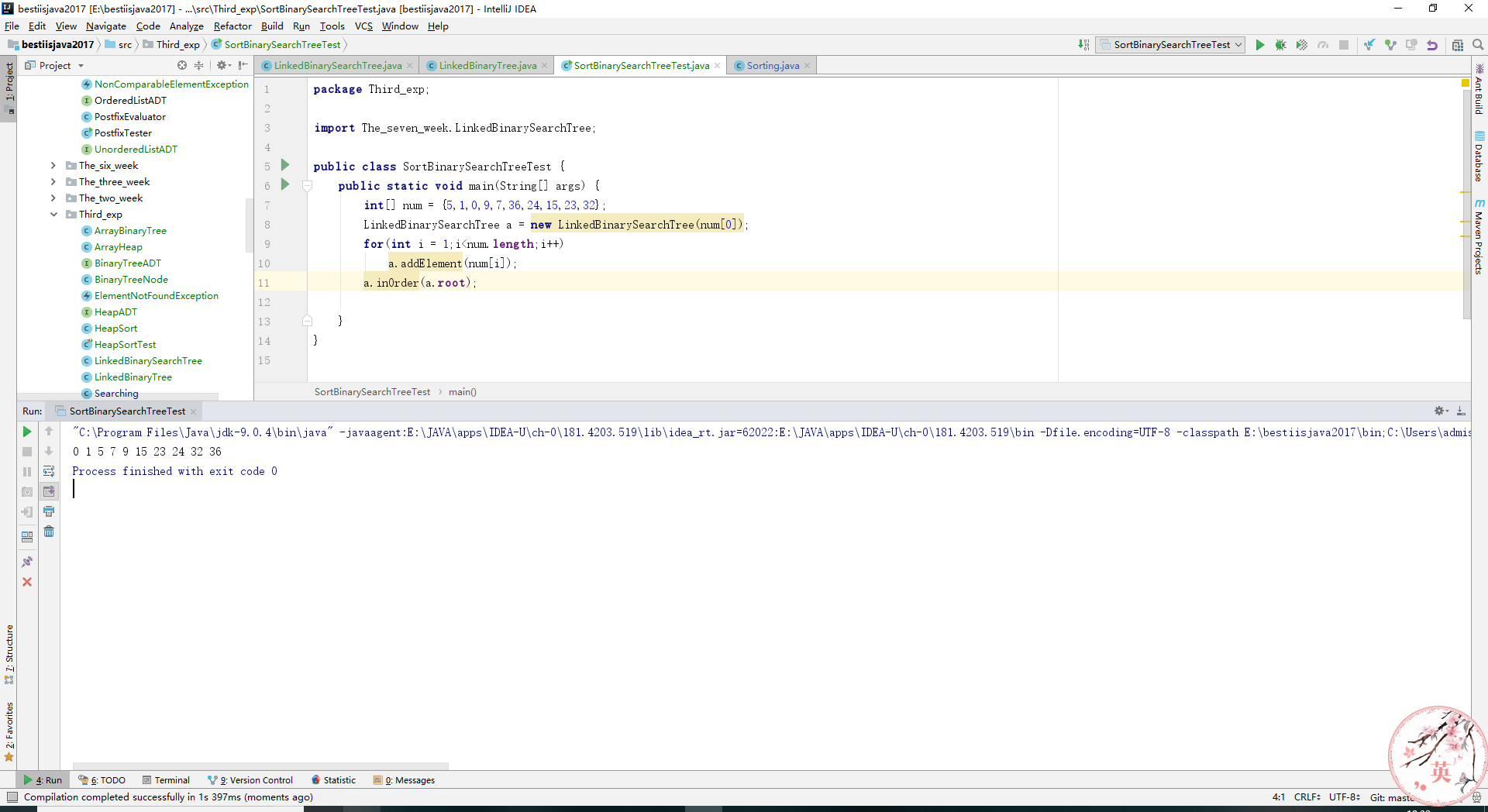
public static void main(String[] args) {
int[] num = {5,1,0,9,7,36,24,15,23,32};
LinkedBinarySearchTree a = new LinkedBinarySearchTree(num[0]);
for(int i = 1;i<num.length;i++)
a.addElement(num[i]);
a.inOrder(a.root);
System.out.println();
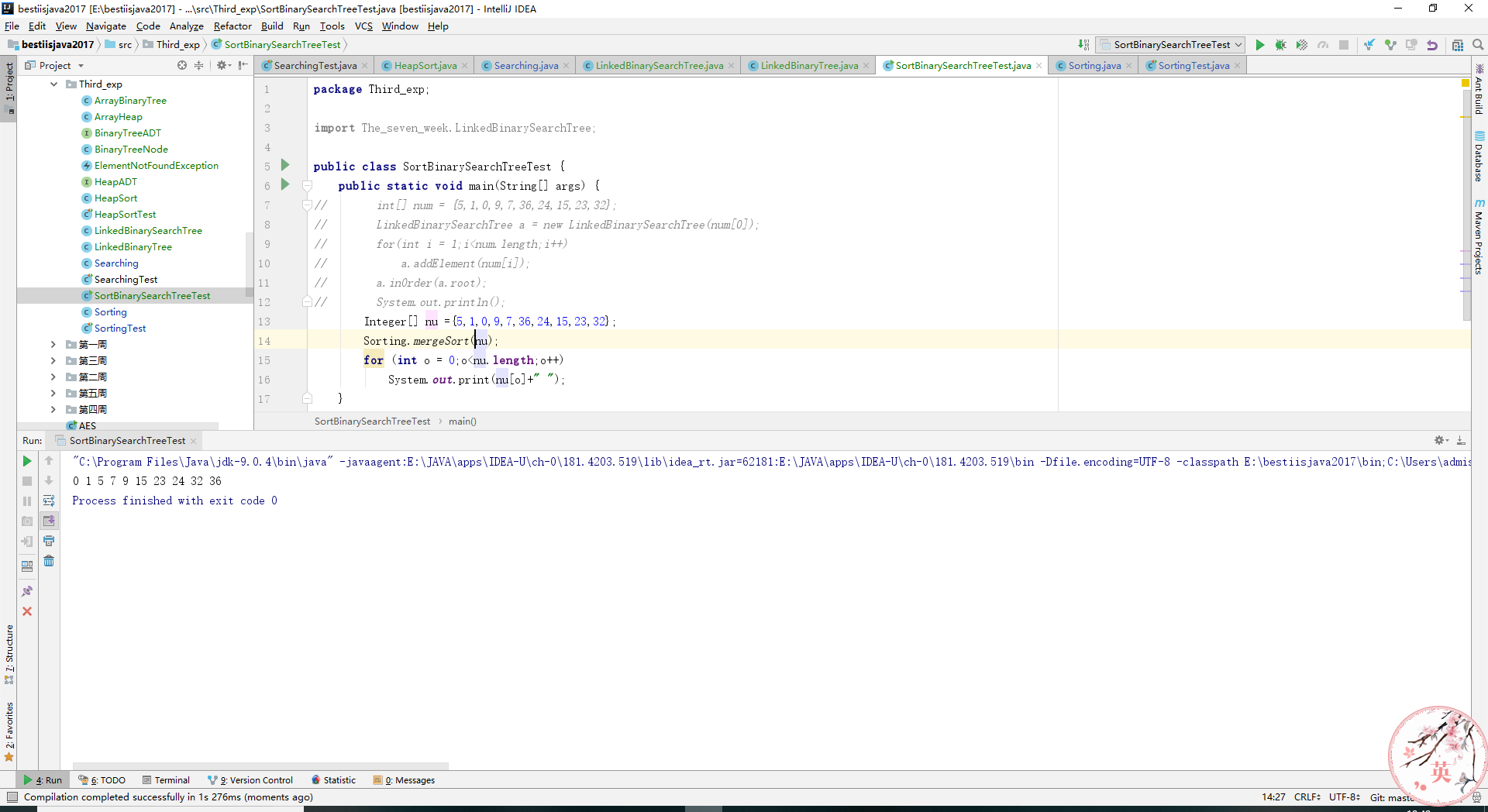
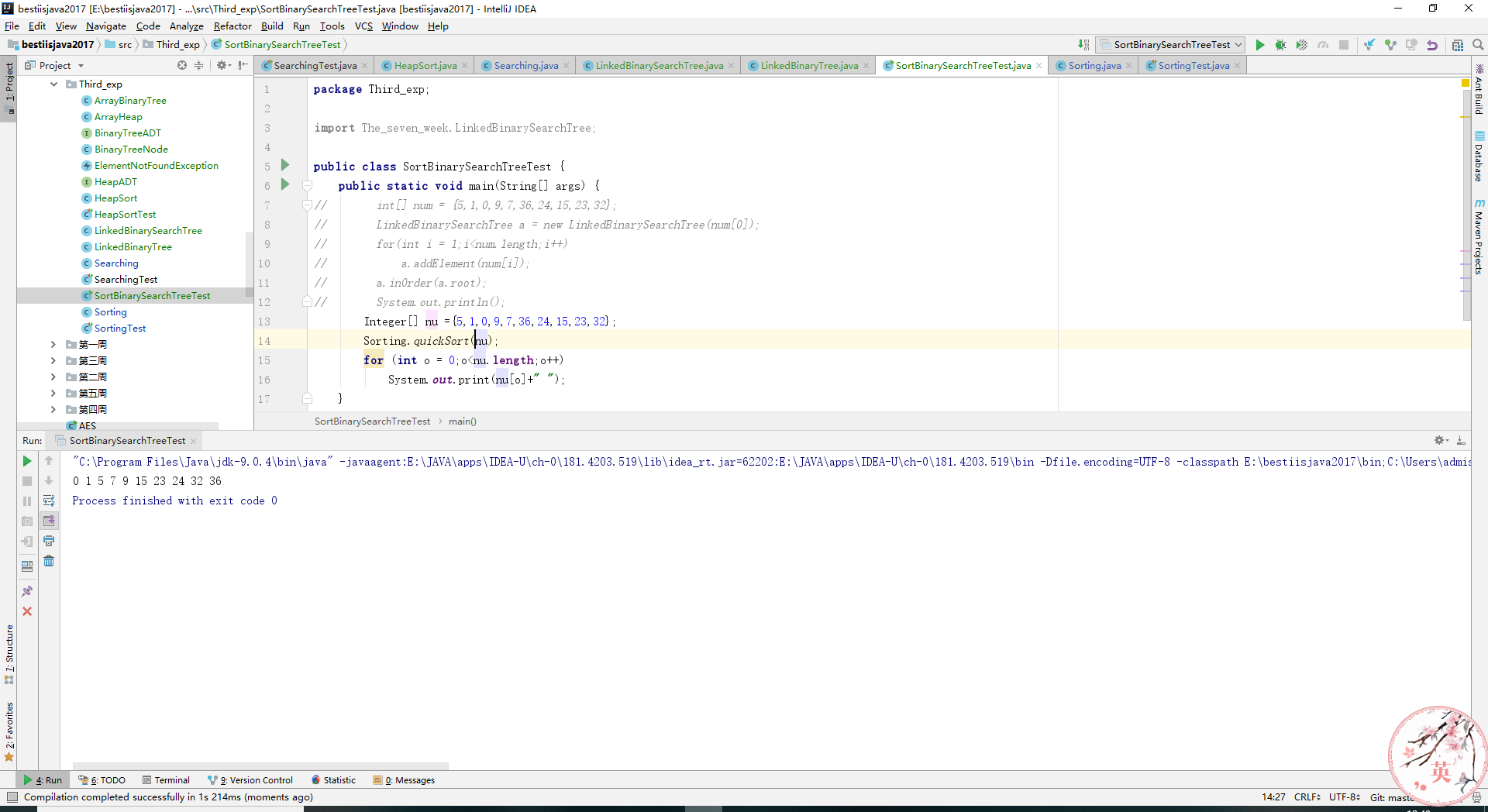
Integer[] nu ={5,1,0,9,7,36,24,15,23,32};
Sorting.quickSort(nu);
for (int o = 0;o<nu.length;o++)
System.out.print(nu[o]+" ");
Sorting.insertionSort(nu);
for (int o = 0;o<nu.length;o++)
System.out.print(nu[o]+" ");
Sorting.selectionSort(nu);
for (int o = 0;o<nu.length;o++)
System.out.print(nu[o]+" ");
Sorting.bubbleSort(nu);
for (int o = 0;o<nu.length;o++)
System.out.print(nu[o]+" ");
Sorting.mergeSort(nu);
for (int o = 0;o<nu.length;o++)
System.out.print(nu[o]+" ");
}
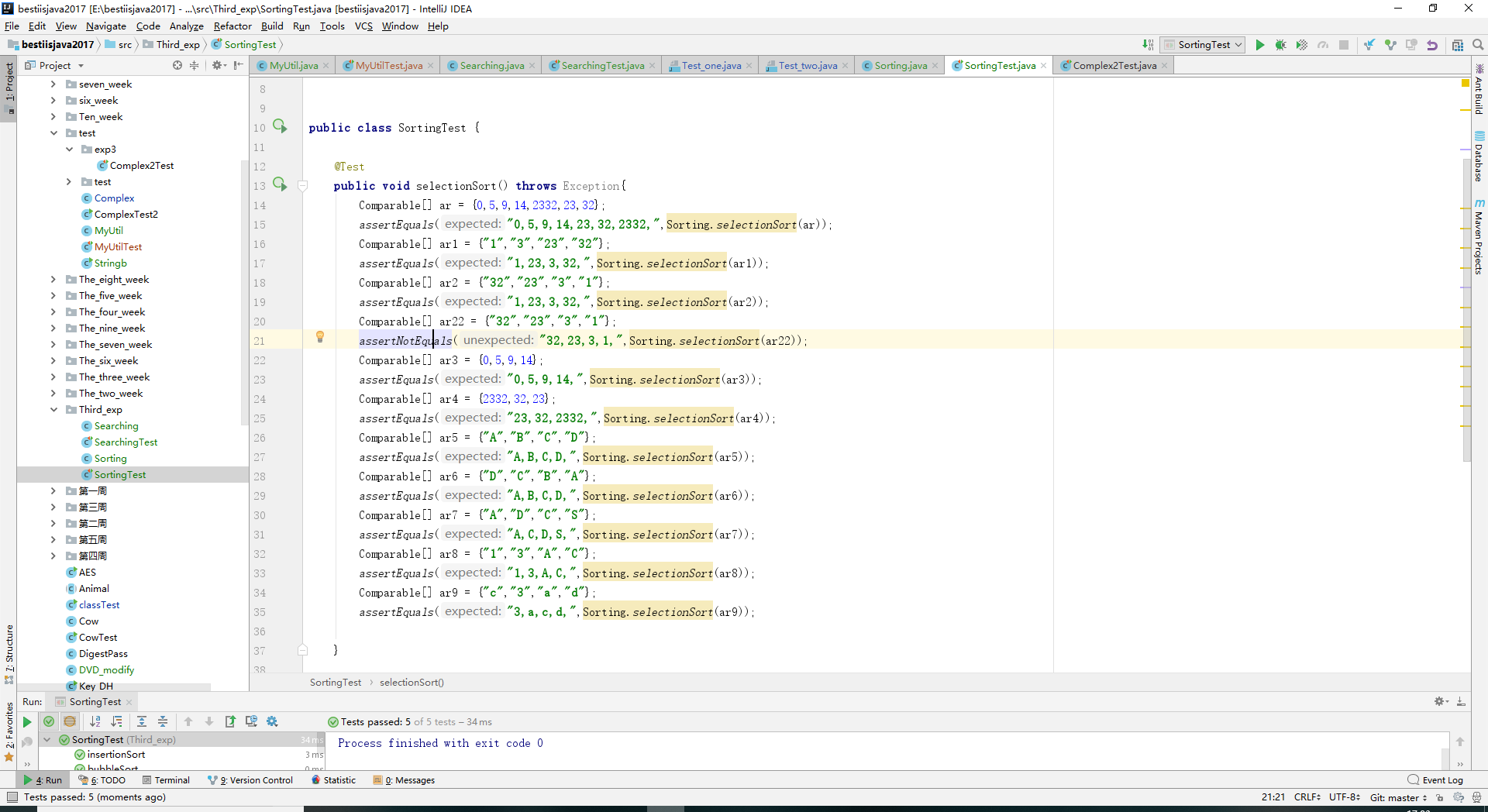
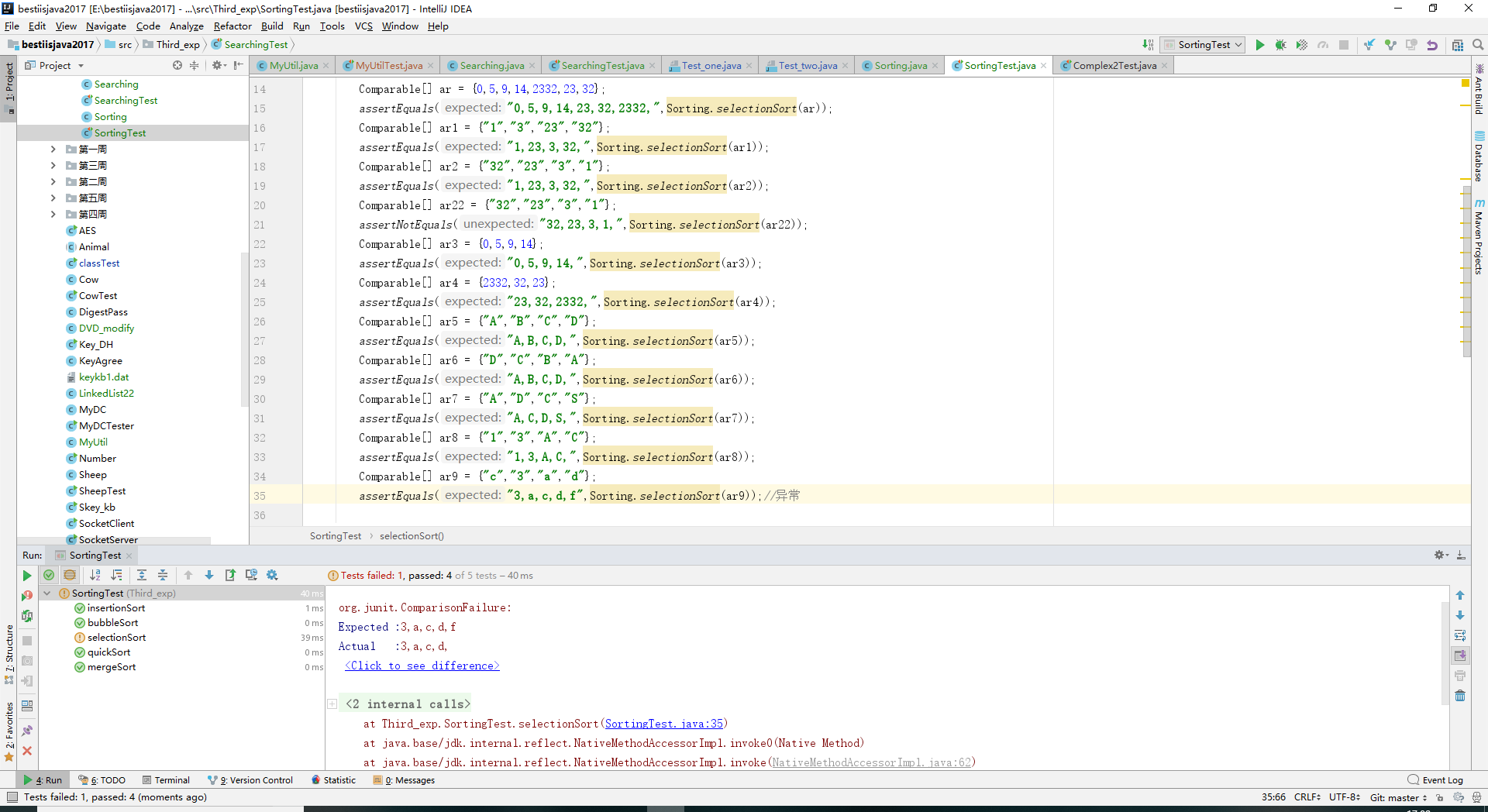
- 实验结果:
- 实验五
- 关键代码:
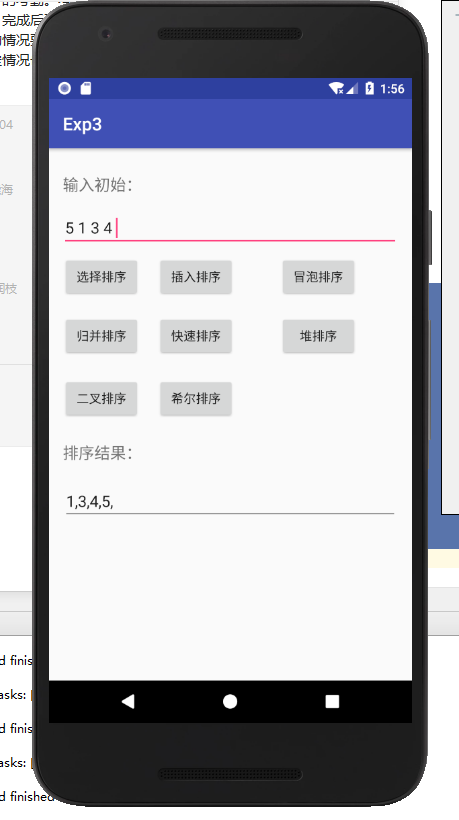
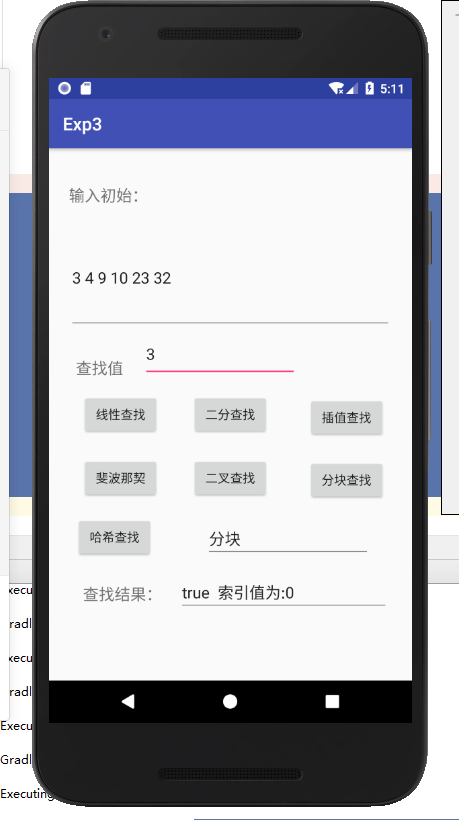
基本与idea中的没变,只是加了布局文件。 - 实验结果:
- 关键代码:
3. 实验过程中遇到的问题和解决过程
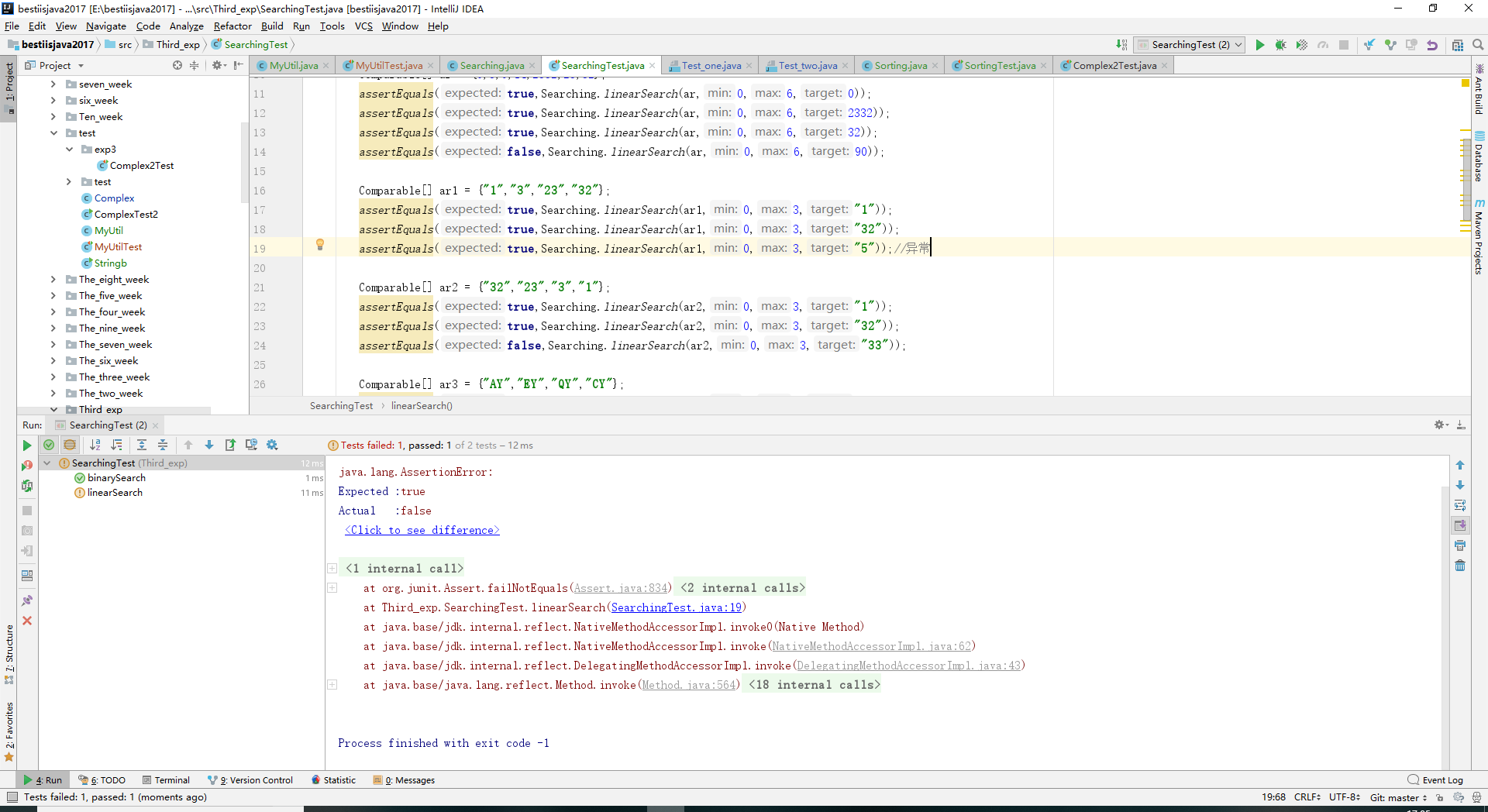
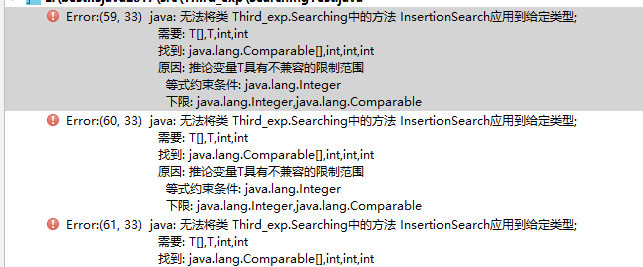
- 问题1:
- 问题1解决方案:T不兼容Comparable型,所以需要改为Integer型的数组。
其他(感悟、思考等)
- 我觉得这次的实验因为学完的太久了,所以有些方法不记得原理了,就又翻了一遍书,正好温习了一下。但是实验整体的难度并不大,原理都清楚就是代码实现的问题,需要花一些时间。