索引算法的应用

索引算法是计算机科学中常见的一类算法，旨在优化数据的查找和访问效率，从而提高计算机程序的性能。

通常情况下，当我们需要查找或获取某个数据时，如果数据量很大，那么在没有索引的情况下，需要遍历整个数据集才能找到所需的数据，这会导致查询时间过长和性能下降。而索引算法则是为了解决这个问题，通过构建和维护索引结构，以快速定位和访问数据。

以下是一些具体的索引算法、数据结构介绍：

二叉树

二叉树是一种树状结构，它的每个节点最多有两个子节点。二叉树是一种非常常见的数据结构，可以通过前序、中序、后续遍历确定树的形状，其既有链表的快速插入与删除操作的特点，又有数组快速查找的优势，同时，因为本身二叉搜索树是有序的(参考前序、中序、后序排列)，所以也支持范围查找。它可以被用于构建各种不同的数据结构和算法，例如二叉搜索树、堆等。下面图一是满二叉树，图二是有序递增集合场景退化成链表，实际使用时会优先考虑平衡二叉树。

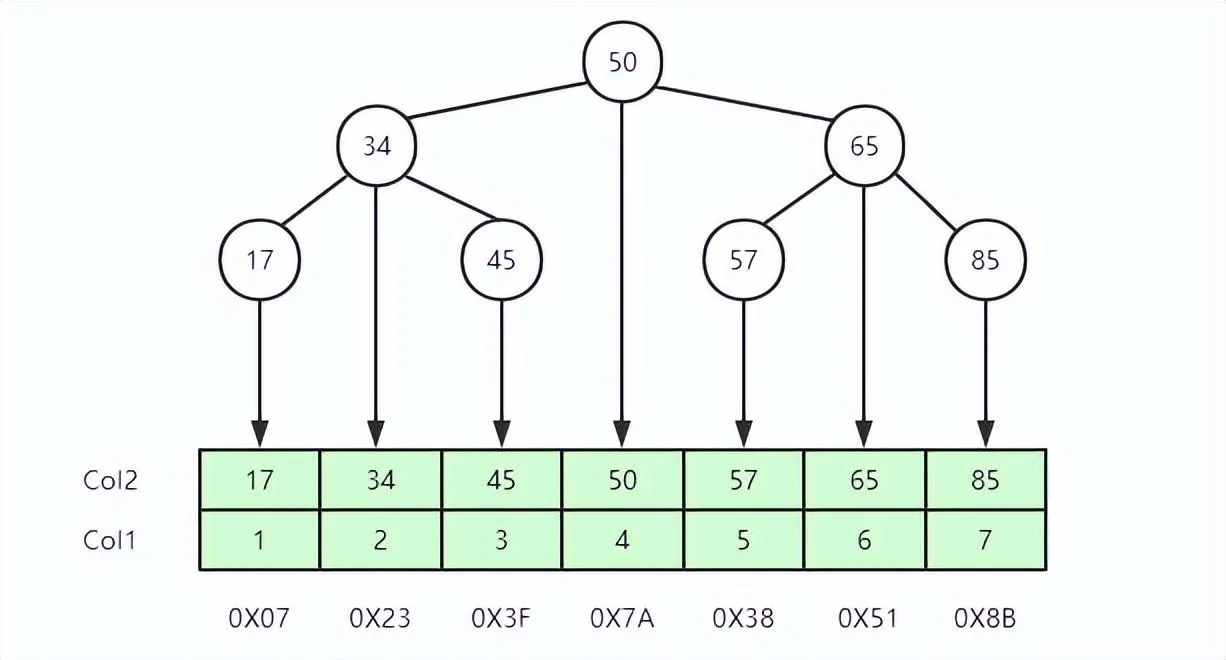
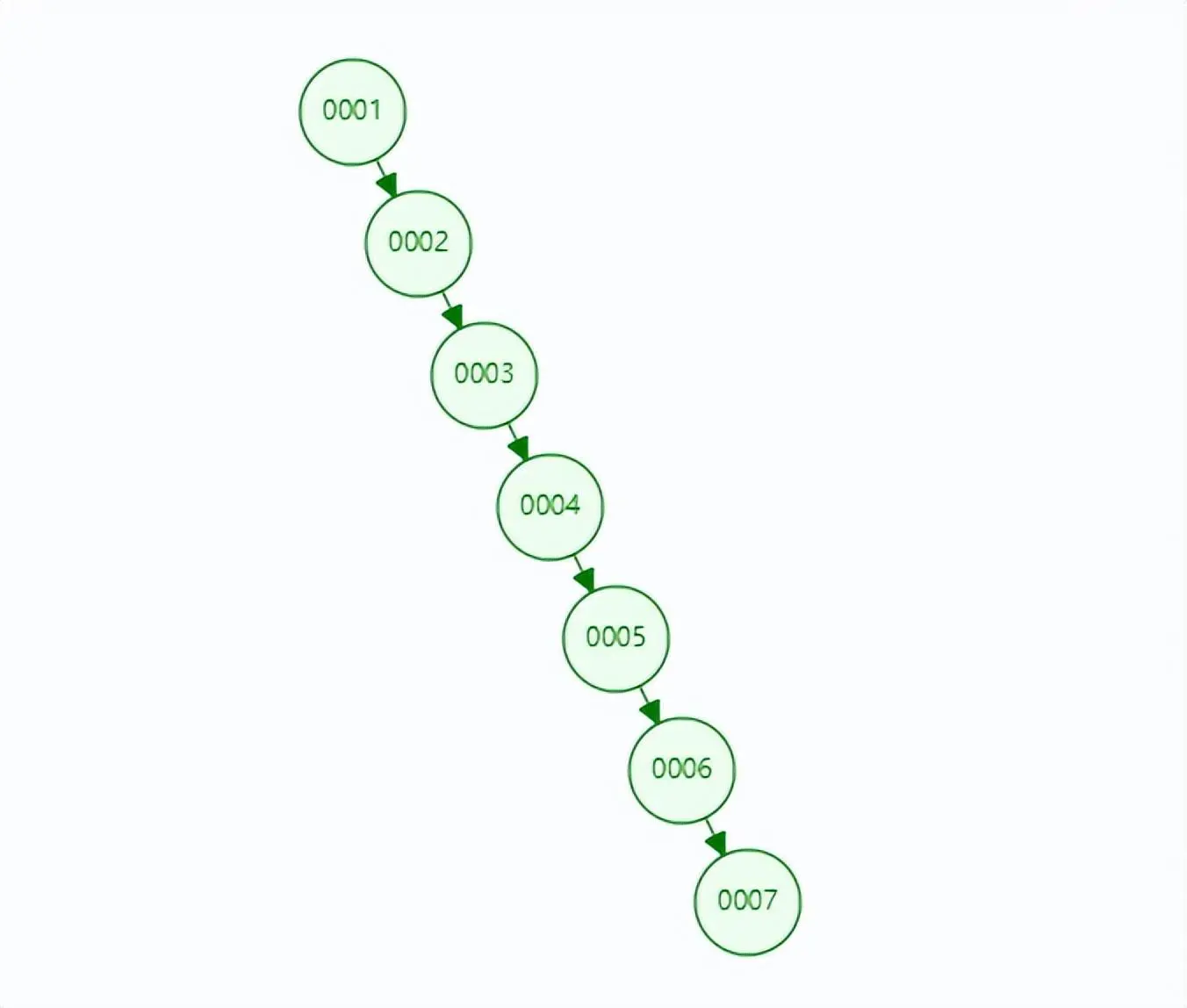
平衡二叉树作为做数据索引好像也是个不错的选择，其实不然，主要是二叉树在深度方面具有不确定性：
一般来说，索引以及对应的原生数据是存在于磁盘中，每次读数都要从磁盘中查出相应的结点，然而二叉树的结点在文件中是随机存放的，所以可能读取一个结点就需要一个磁盘IO，而且二叉树都会比较高（尤其数据多的时候），如一棵一百万个元素的平衡二叉树就有十几层高度了，也就是大部分情况下检索一次数据就需要十几次磁盘IO，这个代价太高了，所以一般二叉树也不会被用来作索引。为了让一个查询尽量少地读磁盘，就必须让查询过程访问尽量少的数据块，也就是说，尽可能的让树的高度变低，也就是用多路搜索树，而MySQL的InnoDB存储引擎使用的就是这种多路搜索树，也就是我们常说的B+树。

红黑树

红黑树是一种自平衡的二叉搜索树，每个节点有红或黑两种颜色。通过保持规则来保持平衡性，它可以支持高效的插入、删除和查找操作。但红黑树也有缺点，当存储大数据量时，树的高度就会变的不可控， 数量越大，树的高度越高，查询的效率将会大大降低。

AVL树

AVL树也是一种自平衡的二叉搜索树，与红黑树相比，它更加平衡，但需要更多的旋转操作。

B树

B树（B-Tree）是一种自平衡树，B树是二叉树的升级版，又叫平衡多路查找树。它和平衡二叉树的区别在于：

• 平衡二叉树最多两个子树，而 B 树每个节点都可以有多个子树，M 阶 B 树表示每个节点最多有M个子树。
• 平衡二叉树每个节点只有一个数据和两个指向孩子的指针，而 B 树每个中间节点有 k-1 个关键字（可以理解为数据）和 k 个子树（ k 介于阶数 M 和 M/2 之间，M/2 向上取整）。
• 所有叶子节点均在同一层、叶子节点除了包含关键字和关键字记录的指针外也有指向其子节点的指针，只不过其指针地址都为 null 。
  B树可用于维护元素有序的数据库或文件系统索引，可以在磁盘等外部存储上有效地维护大量数据。
  

B+树

B+树是B树的变种，所具有的特点：

• 非叶子节点不存储data，只存储索引(冗余)，可以放更多的索引；
• 叶子节点包含所有索引字段；
• 叶子节点用指针连接，提高区间访问的性能。
  
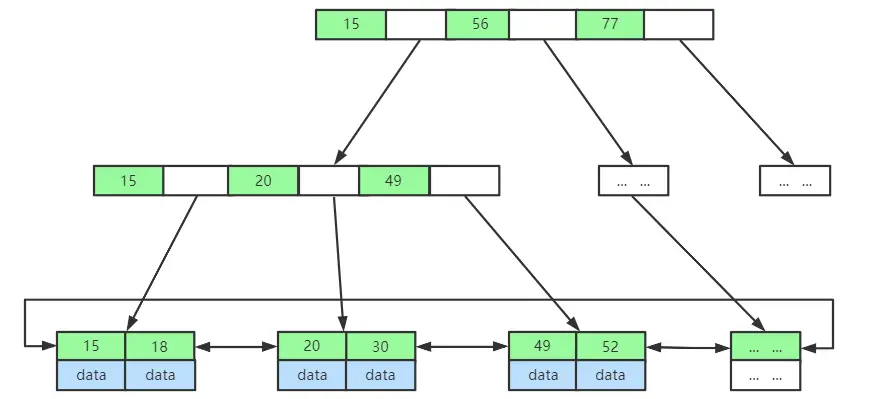
  备注：与红黑树相比，B-Tree和B+Tree两种数据结构都更加矮胖，两种数据结构都是为了减少磁盘 I/O 读写过于频繁而生，本身节点的个数是有限的，采用多叉结构就是为了让每一层放尽可能多的节点以此来降低整棵树的高度。
  为什么MySQL的InnoDB 索引结构最终选择了B+Tree而不是B-Tree呢？
• B+树的磁盘读写代价更低: B+树内部非叶子节点本身并不存储数据，所以非叶子节点的存储代价相比 B树就小的多。存储容量减少同时也缩小了占用盘块的数量，那么数据的聚集程度直接也影响了查询磁盘的次数。
• B+树查询效率更加稳定: 树高确定的前提下所有的数据都在叶子节点，那么无论怎么查询所有关键字查询的路径长度是固定的。
• B+树对范围查询的支持更好: B+树所有数据都在叶子节点，非叶子节点都是索引，那么做范围查询的时候只需要扫描一遍叶子节点即可；而 B树因为非叶子节点也保存数据，范围查询的时候要找到具体数据还需要进行一次中序遍历。

T树

T树是一种用于存储和管理数据的多路平衡搜索树，它是B树的变种。与B树不同的是，T树不是将数据项存储在每个节点上，而是将数据项存储在节点间的边上。因此，T树可以更高效地使用内存，同时具有比B树更快的搜索速度。

哈希表

哈希表是一种以键-值方式存储数据的数据结构，通过索引的key进行一次hash计算，就可以快速获取磁盘文件指针，对于指定索引查找文件非常快，但是对于范围查找没法支持，有时候也会出现Hash冲突（Hash碰撞）的情况。

KD树

KD树是一种用于多维空间的数据结构，它将数据点依次分配在k维坐标系中的每个节点，并在每个节点中选择一个轴对数据进行分割。查询操作通过在树中沿着最近邻点路径搜索来实现。

Suffix Tree

后缀树是一种用于求取字符串中所有后缀的数据结构，它适合于字符串匹配和搜索相关性算法。

倒排索引

倒排索引是一种常用的文本索引算法，它将文档中的每个单词或词组映射到包含该单词或词组的文档列表，可以用于搜索引擎、关键字搜索等应用场景。在倒排索引中，每个单词都对应着若干个文档ID，这些文档ID指向包含该单词的文档。对于文本检索的查询操作，可以先对查询关键字进行分词处理，然后查找包含每个关键字的文档ID，并使用交集或并集等方式得到查询结果。倒排索引的实现可以采用多种数据结构，例如哈希表、有序数组、跳表等。实际中常用的是基于哈希表或有序数组等数据结构的倒排索引实现方式，具有较高的查询效率和较小的空间占用。

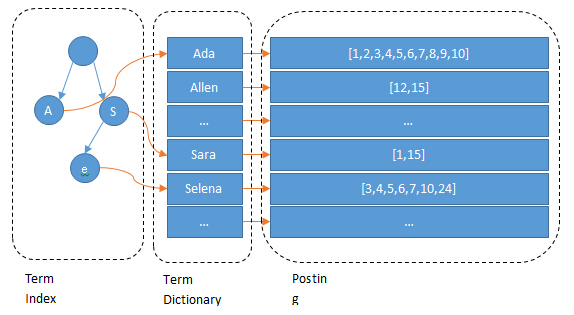
备注：上图为Elasticsearch/Lucene的倒排索引，增加了最左边的一层「字典树」term index，它不存储所有的单词，只存储单词前缀，通过字典树找到单词所在的块，也就是单词的大概位置，再在块里二分查找，找到对应的单词，再找到单词对应的文档列表。此外，Lucene对term index还用了FST（Finite State Transducers）做进一步压缩。

跳表

跳表是建立多级索引，使得查找元素时可以通过跳跃一定的步长，从而提高查找效率。在跳表中，元素按照从小到大的顺序排列，每一个元素都有一个固定的层数，层数越高，该元素对应的索引节点就越多。例如，一个元素的层数为k，则该元素对应的索引节点可以分别为第1层、第2层、...、第k层。