[C++]LeetCode 1971 寻找图中是否存在路径

[C++]LeetCode1971. 寻找图中是否存在路径

题目描述

Difficulty: 简单

Related Topics: 深度优先搜索, 广度优先搜索, 并查集, 图

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [u_i, v_i] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1：

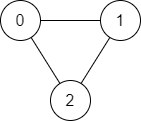
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2 
- 0 → 2

示例 2：

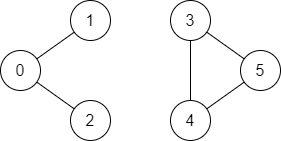
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

提示：

• 1 <= n <= 2 * 10⁵
• 0 <= edges.length <= 2 * 10⁵
• edges[i].length == 2
• 0 <= u_i, v_i <= n - 1
• u_i != v_i
• 0 <= source, destination <= n - 1
• 不存在重复边
• 不存在指向顶点自身的边

思路

并查集

用并查集维护连通性，对每条边[u, v]，将u、v并入同一集合，最后判断起点与终点是否在相同集合即可。

这里并查集的实现比较简单，时间复杂度为\(O(m+n\log n)\)，如果按秩合并/启发式合并复杂度是\(O(m+n\alpha(n))\)。

空间复杂度\(O(n)\)。

Code

Language: C++

class Solution {
        static const int N = 2e5 + 5;
        int fa[N];
        int getfa(int u) {
            return fa[u] == u ? u : fa[u] = getfa(fa[u]);
        }
    public:
        bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
            for (int i = 0; i < n; ++i) fa[i] = i;
            for (const auto& e : edges) {
                if (getfa(e[0]) != getfa(e[1])) fa[getfa(e[0])] = getfa(e[1]);
            }
            return getfa(source) == getfa(destination);
        }
};