数据结构的扩张
一.扩张数据结构
1.目的:给基本数据结构进行扩张以支持一些附加功能或者利用附加信息加速已有的操作
2.基本步骤(可以用于检查和纠错)
(1)选择一种基础的数据结构(红黑树,树,链表,队列等)
(2)确定基础数据结构中要维护的附加信息(具体数据,或属性,或指针类信息等)
(3)检验基础数据结构上的基本修改操作是否能维护附加信息(保证数据结构的运行效率)
(4)设计一些新的操作
二.动态顺序统计
1.顺序统计树:在每个结点上存储附加信息(以x为根的子树(包括x本身)的节点数size)的一棵红黑树
2.一个元素的秩为在中序遍历树时输出的位置
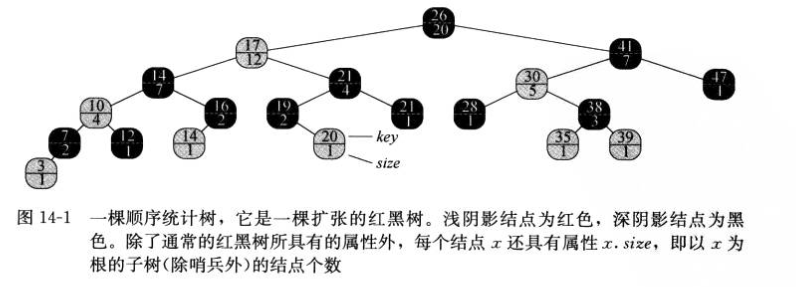
3.分析
(1)选择基础数据结构--红黑树
(2)添加节点附加信息--size
(3)保证删除,插入等操作都能在O(lg n)时间内维护size属性
(4)设计新的操作-select和rank
查找具有给定秩的元素,



1 class Node: 2 def __init__(self, key, right, left, p, color, size): 3 self.key = key 4 self.right = right 5 self.left = left 6 self.p = p 7 self.color = color 8 self.size = size 9 10 11 class tree: 12 def __init__(self, root, nil): 13 self.root = root 14 self.nil = nil 15 16 def tree_insert(self, z): 17 y = self.nil 18 x = self.root 19 while x != self.nil: 20 y = x 21 if z.key < x.key: 22 x = x.left 23 else: 24 x = x.right 25 z.p = y 26 if y == self.nil: 27 self.root = z 28 elif z.key < y.key: 29 y.left = z 30 else: 31 y.right = z 32 z.left = self.nil 33 z.right = self.nil 34 z.color = "RED" 35 # z插入成功后,size初始化为1 36 z.size = 1 37 # 红黑树性质维护 38 self.rb_insert_fixup(z) 39 # 更新结点z的父结点直到根结点的size属性 40 while z.p != self.nil: 41 z.p.size += 1 42 z = z.p 43 44 def left_rotate(self, x): 45 y = x.right 46 x.right = y.left 47 if y.left != self.nil: 48 y.left.p = x 49 y.p = x.p 50 if x.p == self.nil: 51 self.root = y 52 elif x == x.p.left: 53 x.p.left = y 54 else: 55 x.p.right = y 56 y.left = x 57 x.p = y 58 # 左旋导致两个结点的size属性失效,size属性更新如下: 59 y.size = x.size 60 x.size = x.left.size + x.right.size + 1 61 62 def right_rotate(self, y): 63 x = y.left 64 y.left = x.right 65 if x.right != self.nil: 66 x.right.p = y 67 x.p = y.p 68 if y.p == self.nil: 69 self.root = x 70 elif y == y.p.left: 71 y.p.left = x 72 else: 73 y.p.right = x 74 x.right = y 75 y.p = x 76 # 右旋导致两个结点的size属性失效,size属性更新如下: 77 x.size = y.size 78 y.size = y.right.size + y.left.size + 1 79 80 def rb_insert_fixup(self, z): 81 while z.p.color == "RED": 82 if z.p == z.p.p.left: 83 y = z.p.p.right 84 if y.color == "RED": 85 z.p.color = "BLACK" 86 y.color = "BLACK" 87 z.p.p.color = "RED" 88 z = z.p.p 89 else: 90 if z == z.p.right: 91 z = z.p 92 self.left_rotate(z) 93 z.p.color = "BLACK" 94 z.p.p.color = "RED" 95 self.right_rotate(z.p.p) 96 else: 97 y = z.p.p.left 98 if y.color == "RED": 99 z.p.color = "BLACK" 100 y.color = "BLACK" 101 z.p.p.color = "RED" 102 z = z.p.p 103 else: 104 if z == z.p.left: 105 z = z.p 106 self.right_rotate(z) 107 z.p.color = "BLACK" 108 z.p.p.color = "RED" 109 self.left_rotate(z.p.p) 110 self.root.color = "BLACK" 111 112 def inorder_tree_walk(self, x): 113 if x != self.nil: 114 self.inorder_tree_walk(x.left) 115 print(x.key) 116 self.inorder_tree_walk(x.right) 117 118 def tree_search(self, x, k): 119 if x == self.nil or k == x.key: 120 return x 121 if k < x.key: 122 return self.tree_search(x.left, k) 123 else: 124 return self.tree_search(x.right, k) 125 126 def rb_transplant(self, u, v): 127 if u.p == self.nil: 128 self.root = v 129 elif u == u.p.left: 130 u.p.left = v 131 else: 132 u.p.right = v 133 v.p = u.p 134 135 def tree_minimum(self, x): 136 while x.left != self.nil: 137 x = x.left 138 return x 139 140 def rb_delete(self, z): 141 y = z 142 y_original_color = y.color 143 if z.left == self.nil: 144 x = z.right 145 self.rb_transplant(z, z.right) 146 elif z.right == self.nil: 147 x = z.left 148 self.rb_transplant(z, z.left) 149 else: 150 y = self.tree_minimum(z.right) 151 y_original_color = y.color 152 x = y.right 153 if y.p == z: 154 x.p = y 155 else: 156 self.rb_transplant(y, y.right) 157 y.right = z.right 158 y.right.p = y 159 self.rb_transplant(z, y) 160 y.left = z.left 161 y.left.p = y 162 y.color = z.color 163 if y_original_color == "BLACK": 164 self.rb_delete_fixup(x) 165 166 def rb_delete_fixup(self, x): 167 while x != self.root and x.color == "BLACK": 168 if x == x.p.left: 169 w = x.p.right 170 if w.color == "RED": 171 w.color = "BLACK" 172 x.p.color = "RED" 173 self.left_rotate(x.p) 174 w = x.p.right 175 if w.left.color == "BLACK" and w.right.color == "BLACK": 176 w.color = "RED" 177 x = x.p 178 else: 179 if w.right.color == "BLACK": 180 w.left.color == "BLACK" 181 w.color = "RED" 182 self.right_rotate(w) 183 w = x.p.right 184 w.color = x.p.color 185 x.p.color = "BLACK" 186 w.right.color = "BLACK" 187 self.left_rotate(x.p) 188 x = self.root 189 else: 190 w = x.p.left 191 if w.color == "RED": 192 w.color = "BLACK" 193 x.p.color = "RED" 194 self.right_rotate(x.p) 195 w = x.p.left 196 if w.right.color == "BLACK" and w.left.color == "BLACK": 197 w.color = "RED" 198 x = x.p 199 else: 200 if w.left.color == "BLACK": 201 w.right.color == "BLACK" 202 w.color = "RED" 203 self.left_rotate(w) 204 w = x.p.left 205 w.color = x.p.color 206 x.p.color = "BLACK" 207 w.left.color = "BLACK" 208 self.right_rotate(x.p) 209 x = self.root 210 x.color = "BLACK" 211 212 def print_tree(self, z): 213 if z != self.nil: 214 print(z.key, z.color, ":", end='') 215 print("( ", end='') 216 print(z.left.key, z.left.color, " ", end='') 217 print(z.right.key, z.right.color, end='') 218 print(" )", end='') 219 220 # 找出统计树中的第i小的关键字 221 def os_select(self, x, i): 222 r = x.left.size + 1 223 if i == r: 224 return x 225 elif x < r: 226 return self.os_select(x.left, i) 227 else: 228 # 注意这种情况就应该找以x为根结点的右子树中第i-r小的关键字了。 229 return self.os_select(x.right, i - r) 230 231 # 确定一个元素的秩:返回对T中序遍历对应的线性序中x的位置 232 def os_rank(self, x): 233 r = x.left.size + 1 234 y = x 235 while y != self.root: 236 if y == y.p.right: 237 r += y.p.left.size + 1 238 y = y.p 239 return r
三.区间树
1.区间树是对动态集合进行维护的红黑树,其中每个元素x都包含一个区间x.int
 fe
fe
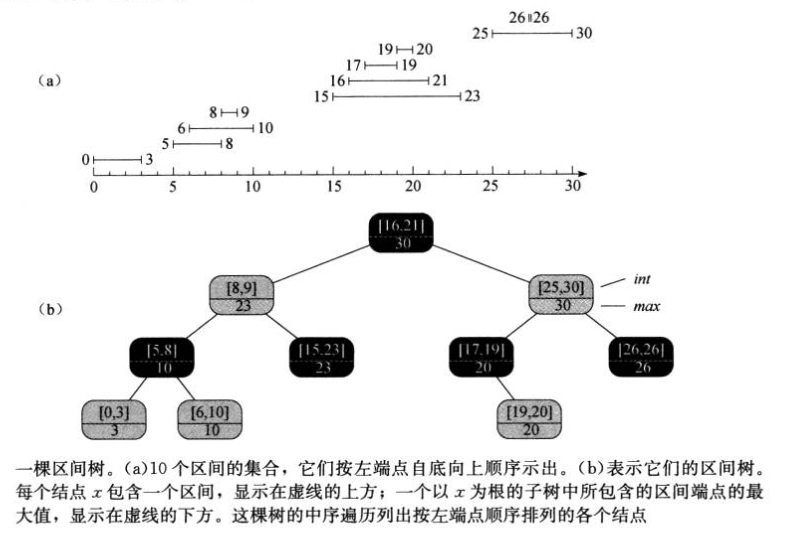
2.分析:
(1)选择基础数据结构--红黑树
(2)添加节点附加信息--以x为根的子树中所有区间的端点的最大值x.max
(3)对信息的维护--插入和删除操作能否在O(lgn)时间内完成
(4)设计新的操作-insert,delete,search


1 class Node: 2 def __init__(self,right,left,p,color,inter,maxx): 3 self.key=inter.low 4 self.right=right 5 self.left=left 6 self.p=p 7 self.color=color 8 #新增区间属性 9 self.inter=inter 10 #新增附加信息maxx 11 self.maxx=maxx 12 13 #代表区间的类 14 class Inter: 15 def __init__(self,low,high): 16 self.low=low 17 self.high=high 18 19 class tree: 20 def __init__(self,root,nil): 21 self.root=root 22 self.nil=nil 23 def tree_insert(self,z): 24 y=self.nil 25 x=self.root 26 while x!=self.nil: 27 y=x 28 if z.key<x.key: 29 x=x.left 30 else: 31 x=x.right 32 z.p=y 33 if y==self.nil: 34 self.root=z 35 elif z.key<y.key: 36 y.left=z 37 else: 38 y.right=z 39 z.left=self.nil 40 z.right=self.nil 41 z.color="RED" 42 z.maxx=max(z.inter.high,z.left.maxx,z.right.maxx) 43 #红黑树性质维护 44 self.rb_insert_fixup(z) 45 #更新父结点直到根结点的maxx 46 while z.p!=self.nil: 47 z.p.maxx=max(z.p.maxx,z.maxx) 48 z=z.p 49 50 def left_rotate(self,x): 51 y=x.right 52 x.right=y.left 53 if y.left!=self.nil: 54 y.left.p=x 55 y.p=x.p 56 if x.p==self.nil: 57 self.root=y 58 elif x==x.p.left: 59 x.p.left=y 60 else: 61 x.p.right=y 62 y.left=x 63 x.p=y 64 #左旋导致两个结点的max属性改变,更新如下 65 y.maxx=x.maxx 66 x.maxx=max(x.left.maxx,x.right.maxx,x.inter.high) 67 68 69 def right_rotate(self,y): 70 x=y.left 71 y.left=x.right 72 if x.right!=self.nil: 73 x.right.p=y 74 x.p=y.p 75 if y.p==self.nil: 76 self.root=x 77 elif y==y.p.left: 78 y.p.left=x 79 else: 80 y.p.right=x 81 x.right=y 82 y.p=x 83 #右旋导致两个结点的max属性改变,更新如下 84 x.maxx=y.maxx 85 y.maxx=max(y.right.maxx,y.left.maxx,y.inter.high) 86 87 def rb_insert_fixup(self,z): 88 while z.p.color=="RED": 89 if z.p==z.p.p.left: 90 y=z.p.p.right 91 if y.color=="RED": 92 z.p.color="BLACK" 93 y.color="BLACK" 94 z.p.p.color="RED" 95 z=z.p.p 96 else: 97 if z==z.p.right: 98 z=z.p 99 self.left_rotate(z) 100 z.p.color="BLACK" 101 z.p.p.color="RED" 102 self.right_rotate(z.p.p) 103 else: 104 y=z.p.p.left 105 if y.color=="RED": 106 z.p.color="BLACK" 107 y.color="BLACK" 108 z.p.p.color="RED" 109 z=z.p.p 110 else: 111 if z==z.p.left: 112 z=z.p 113 self.right_rotate(z) 114 z.p.color="BLACK" 115 z.p.p.color="RED" 116 self.left_rotate(z.p.p) 117 self.root.color="BLACK" 118 def inorder_tree_walk(self,x): 119 if x!=self.nil: 120 self.inorder_tree_walk(x.left) 121 print(x.key) 122 self.inorder_tree_walk(x.right) 123 def tree_search(self,x,k): 124 if x==self.nil or k==x.key: 125 return x 126 if k < x.key: 127 return self.tree_search(x.left,k) 128 else: return self.tree_search(x.right,k) 129 130 def rb_transplant(self,u,v): 131 if u.p==self.nil: 132 self.root=v 133 elif u==u.p.left: 134 u.p.left=v 135 else: 136 u.p.right=v 137 v.p=u.p 138 def tree_minimum(self,x): 139 while x.left!=self.nil: 140 x=x.left 141 return x 142 143 144 def rb_delete(self,z): 145 y=z 146 y_original_color=y.color 147 if z.left==self.nil: 148 x=z.right 149 self.rb_transplant(z,z.right) 150 elif z.right==self.nil: 151 x=z.left 152 self.rb_transplant(z,z.left) 153 else: 154 y=self.tree_minimum(z.right) 155 y_original_color=y.color 156 x=y.right 157 if y.p==z: 158 x.p=y 159 else: 160 self.rb_transplant(y,y.right) 161 y.right=z.right 162 y.right.p=y 163 self.rb_transplant(z,y) 164 y.left=z.left 165 y.left.p=y 166 y.color=z.color 167 if y_original_color=="BLACK": 168 self.rb_delete_fixup(x) 169 170 171 def rb_delete_fixup(self,x): 172 while x!=self.root and x.color=="BLACK": 173 if x==x.p.left: 174 w=x.p.right 175 if w.color=="RED": 176 w.color="BLACK" 177 x.p.color="RED" 178 self.left_rotate(x.p) 179 w=x.p.right 180 if w.left.color=="BLACK" and w.right.color=="BLACK": 181 w.color="RED" 182 x=x.p 183 else: 184 if w.right.color=="BLACK": 185 w.left.color=="BLACK" 186 w.color="RED" 187 self.right_rotate(w) 188 w=x.p.right 189 w.color=x.p.color 190 x.p.color="BLACK" 191 w.right.color="BLACK" 192 self.left_rotate(x.p) 193 x=self.root 194 else: 195 w=x.p.left 196 if w.color=="RED": 197 w.color="BLACK" 198 x.p.color="RED" 199 self.right_rotate(x.p) 200 w=x.p.left 201 if w.right.color=="BLACK" and w.left.color=="BLACK": 202 w.color="RED" 203 x=x.p 204 else: 205 if w.left.color=="BLACK": 206 w.right.color=="BLACK" 207 w.color="RED" 208 self.left_rotate(w) 209 w=x.p.left 210 w.color=x.p.color 211 x.p.color="BLACK" 212 w.left.color="BLACK" 213 self.right_rotate(x.p) 214 x=self.root 215 x.color="BLACK" 216 217 def print_tree(self,z): 218 if z!=self.nil: 219 print(z.key,z.color,"[",z,inter.low,",",z.inter.high,"]",":",end='') 220 print("( ",end='') 221 print(z.left.key,z.left.color," ",end='') 222 print(z.right.key,z.right.color,end='') 223 print(" )",end='') 224 def interval_search(self,i): 225 x=self.root 226 while x!=self.nil and (i.high<x.inter.low or x.inter.high<i.low): 227 if x.left!=self.nil and x.left.maxx>=i.low: 228 x=x.left 229 else: 230 x=x.right 231 return x 232 233 if __name__=="__main__": 234 inter=Inter(0,0) 235 nil=Node(None,None,None,"BLACK",inter,0) 236 inter=Inter(16,21) 237 root=Node(nil,nil,nil,"BLACK",inter,21) 238 t=tree(root,nil) 239 TT=[8,9,25,30,5,8,15,23,17,19,26,26,0,3,6,10,19,20] 240 for i in range(0,len(TT),2): 241 inter=Inter(TT[i],TT[i+1]) 242 z=Node(nil,nil,nil,"RED",inter,0) 243 t.tree_insert(z)






