递归和迭代

一.递归（Recursion）

1.递归：以相似的方式重复自身的过程

2.递归在程序中表现为：在函数的定义中直接或间接调用函数自身

3.递归和循环：

（1）递归是有去（递去）有回（归来），因为存在终止条件，比如你打开一扇门还有一扇门，不断打开，最终你会碰到一面墙，然后返回

（2）循环是有去无回，但可以设置终止条件，比如你打开一扇门还有一扇门，不断打开，还有门，没有终点

4.递归的递去和归来：

（1）递归的递去：原问题必须可以分解成若干个子问题，而且子问题须与原始问题为同样的事（相似），且规模更小

（2）递归的归来：子问题的演化必须有一个明确的终点，否则可能导致无限递归（无终止条件的循环），也就是说不能无限制地调用本身，须有个出口，化简为非递归状况处理

5.递归在函数中的具体形式：

（1）必须明确终止条件，并给出终止时的处理

（2）必须有间接或直接调用自身解决小规模问题的步骤

def recursion(大规模问题)：

　　if end_condition:                                  #终止条件

　　　　end                                               #终止的处理

　　else:

　　　　recursion(小规模子问题)　　　　#调用自身

6.递归的应用：

（1）问题的定义是按递归定义的（Fibonacci函数，阶乘，…）；

（2） 问题的解法是递归的（有些问题只能使用递归方法来解决，例如，汉诺塔问题，…）；

（3） 数据结构是递归的（链表、树等的操作，包括树的遍历，树的深度，…）

7.递归的优缺点

（1）递归的优点：简洁，容易处理问题，代码可读性高

（2）时间和空间消耗大

8.递归式求解的基本方法

（1）代换法

1.猜对答案

2.用数学归纳法求解常系数，并验证递归式解的正确性

例：已知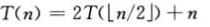：T（n）= O（n lgn）

则计算：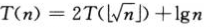

（2）递归树

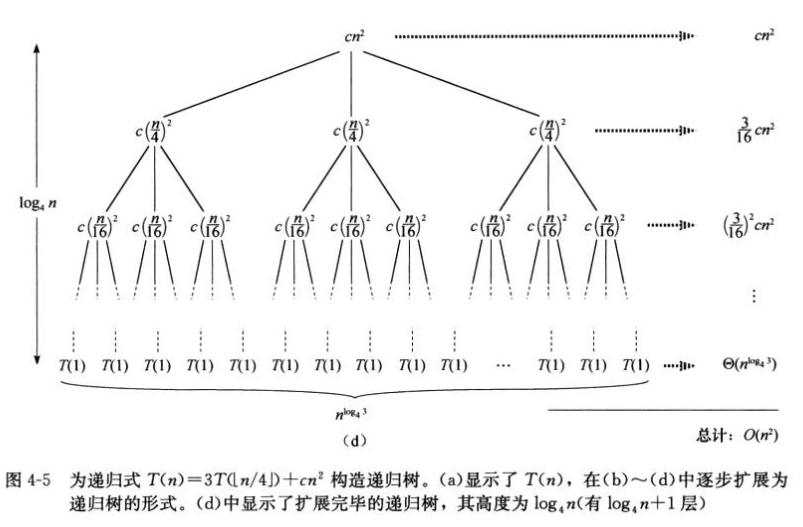
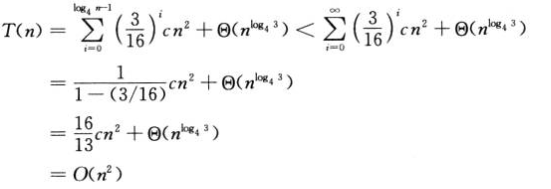
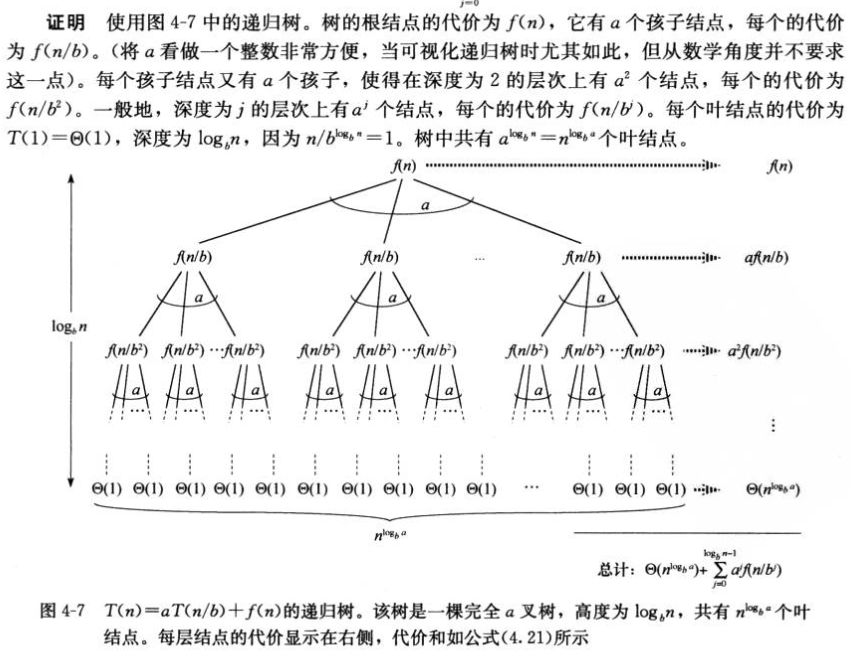
（3）主方法：不是所有情况都包括

 

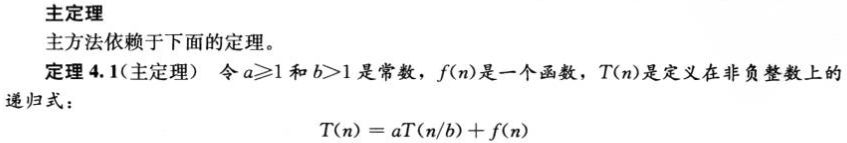
二.迭代

1.迭代：是一种为了逼近所需目标或结果，不断用变量的旧值递推新值的过程

2.迭代在程序中的表现：函数不断调用原函数的返回值，

3.迭代与循环，迭代和递归一样，也是循环的一种

（1）循环：参与运算的变量同时是保存结果的变量

（2）迭代：当前保存的结果作为下一次循环计算的初始值。迭代则使用计数器结束循环。

4.迭代和递归

（1）迭代：函数内某段代码实现循环，函数调用时使用前一次循环的返回值作为初始值，A调用B，使5用计数器结束循环

（2）递归：重复调用自身实现循环，A调用A，设置结束条件

（3）递归中一定有迭代,但是迭代中不一定有递归,大部分可以相互转换.能用迭代的不用递归,

5.迭代在程序中的表示：

（1）必须设置计数器，可以通过计数设置或条件设置，否则会一直迭代

（2）必须有返回值可以作为再次迭代的初值

def iteration(A):

　　return B

C

 

for i in range(n):

　　C=interation(C)

6.迭代的优缺点

（1）优点：代码效率高，时间空间消耗比递归小

（2）缺点：不够简洁，容易混淆