比较排序
一.问题描述
输入:n个数的一个序列<a1,a2,...,an>
输出:输入序列的一个从小到大的排序<a1',a2',...,an'>
二.比较排序
1.在排序的最终结果中,各元素的次序依赖于它们之间的比较
2.快速排序,归并排序,插入排序,堆排序都是比较排序,
3.堆排序和归并排序都是渐近最优的比较排序算法(运行时间上界为O(nlgn))
4.比较排序可以被抽象为一棵决策树,它是一棵完全二叉树,它可以表示在给定输入规模的情况下,某一特定排序算法对所有元素的比较操作
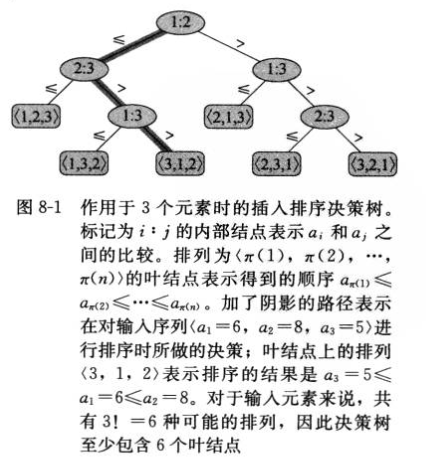
4.最坏情况

三.插入排序
1.简述:对于数组A[1...n]进行排序,对于第j个数,假设前j-1个数已排序好,看成常量,把第j个数依次与第j-1,j-2...0个数进行比较,如果遇到比他小的,插入到对应位置,比他大的数全部依次向后位移一位。按照循环,依次将原序列第1...n个数进行插入排序


1 A=[5,2,4,6,1,3] 2 def Insertion_Sort(A): 3 #把第j个元素插入到【0,j-1】中,从第0个元素开始 4 for j in range(1,len(A)): 5 key=A[j] 6 i=j-1 7 #i从(j-1)到 0,i向前进1,直到要插入元素比前面的元素大 8 # 从第j-1个元素和要插入的元素比较到,从第0个元素和要插入的元素比较 9 while i>=0 and A[i]>key: 10 A[i+1]=A[i] 11 i=i-1 12 A[i+1]=key 13 return A 14 15 print(Insertion_Sort(A)) 16 ------------------------------------ 17 [1, 2, 3, 4, 5, 6]
2.分析:
(1)最坏情况运行时间:输入逆序序列进行排序,
T(n)= 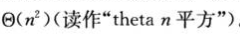
四.归并排序
步骤:
1.如果n=1,则已排序好
2.递归地对A【1...n/2】和A【n/2...n】进行排序(n/2向上取整)
3.把排好序的两个表进行归并

归并步骤需要T(n)=θ(n)(也被称为线性时间)
故总的时间:

即:
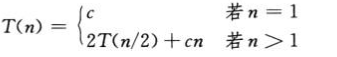
用递归树求解
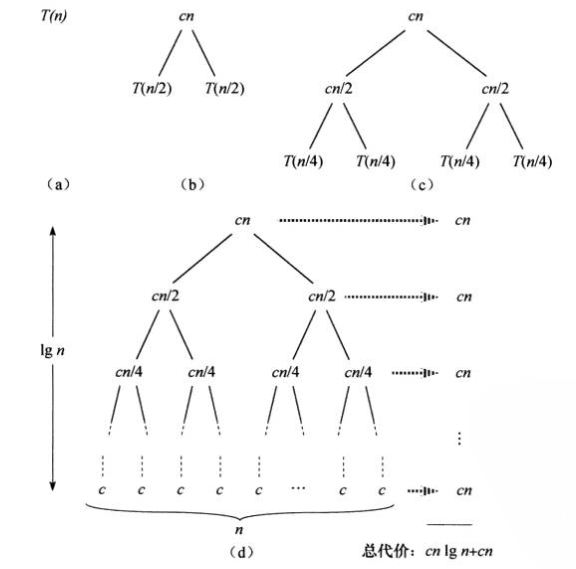
所以最坏时间规模:T(n)=θ(n lgn)(在充分大规模下(30)比n2大)




1 #分治法-并归排序 2 3 def merge(A,p,q,r): 4 #排序A中【p,q】,和【q+1,r】 5 n1=q-p+1 6 n2=r-q 7 L=[] 8 R=[] 9 for i in range(n1): 10 L.append(A[p+i]) 11 for j in range(n2): 12 R.append(A[q+1+j]) 13 L.append(float('inf')) 14 R.append(float('inf')) 15 i=0 16 j=0 17 for k in range(p,r+1): 18 if L[i]<=R[j]: 19 A[k]=L[i] 20 i=i+1 21 else: 22 A[k]=R[j] 23 j=j+1 24 25 import math 26 def merge_sort(A,p,r): 27 #排序A【p,r】 28 if p < r: 29 q = math.floor((p+r)/2)#取整 30 merge_sort(A,p,q) 31 merge_sort(A,q+1,r) 32 merge(A,p,q,r) 33 34 A=[5,2,4,7,1,3,2,6] 35 36 merge_sort(A,0,len(A)-1) 37 38 print(A) 39 ------------------------------------------------ 40 [1, 2, 2, 3, 4, 5, 6, 7]
五.快速排序
1.分治法:
(1)分:选取关键字把原数组分成两部分,而且一部分的值全大于另一部分的值
(2)治:递归处理两部分的排序
(3)合并:直接连接
2.特点:采用分治策略,原地排序,节省空间,改进性强,运行时间是线性时间


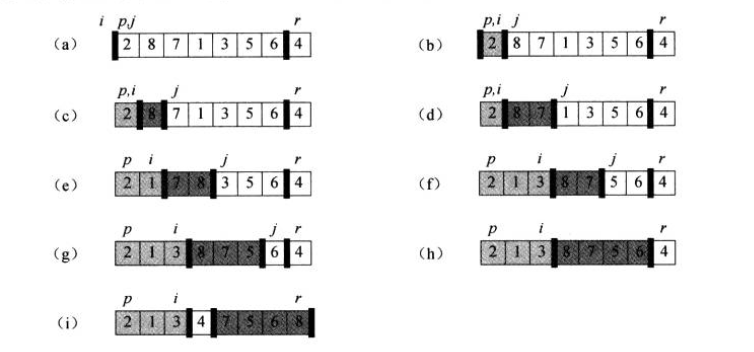
3.假设没有重复元素,
(1)最差情况:输入时顺序或逆序排好的(此时一部分没有元素,一部分是全部元素),
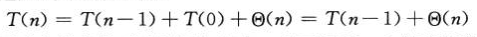

(2)最好情况:分的两部分的规模都不大于n/2

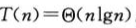
(3)平均情况和最好情况的时间复杂度是一样的

1 #对A[p,r]进行快速排序 2 def quicksort(A, p, r): 3 if p < r: 4 q = partition(A, p, r)#计算分块下标q 5 quicksort(A, p, q - 1)#对前面进行快速排序 6 quicksort(A, q + 1, r)#对后面进行快速排序 7 8 #计算分块下标, 9 def partition(A, p, r): 10 x = A[r]#主元 11 i = p - 1 12 for j in range(p, r): 13 #把每个元素和主元比较, 14 #如果比主元大或等于,不做操作 15 if A[j] < x:#如果比较的元素比主元小, 16 i += 1#把记录的最后一个比主元小的元素的坐标+1 17 A[i],A[j]=A[j],A[i]# 把当前的元素A【j】和A【i】交换 18 #通过A[r]改变A【i+1】 19 A[r] = A[i + 1] 20 A[i + 1] = x 21 return i + 1 22 23 A=[2,8,7,1,3,5,6,4] 24 print(partition(A, 0, 7)) 25 print(A) 26 quicksort(A,0,7) 27 print(A) 28 ---------------------------- 29 3 30 [2, 1, 3, 4, 7, 5, 6, 8] 31 [1, 2, 3, 4, 5, 6, 7, 8]
4.随机化快速排序:随机选取主元
(1)运行时间不依赖于输入序列的顺序,
(2)无需对输入序列的分布做任何假设,
(3)没有一种特定的输入会引起最差的运行效率
(4)最差的情况由随机数产生器决定

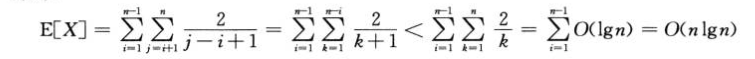

1 #计算分块下标, 2 def partition(A, p, r): 3 x = A[r]#主元 4 i = p - 1 5 for j in range(p, r): 6 #把每个元素和主元比较, 7 #如果比主元大或等于,不做操作 8 if A[j] < x:#如果比较的元素比主元小, 9 i += 1#把记录的最后一个比主元小的元素的坐标+1 10 A[i],A[j]=A[j],A[i]# 把当前的元素A【j】和A【i】交换 11 #通过A[r]改变A【i+1】 12 A[r] = A[i + 1] 13 A[i + 1] = x 14 return i + 1 15 16 import random 17 18 def randomized_quicksort(A, p, r): 19 if p < r: 20 q = randomized_partition(A, p, r) 21 randomized_quicksort(A, p, q - 1) 22 randomized_quicksort(A, q + 1, r) 23 24 def randomized_partition(A, p, r): 25 i = random.randint(p, r) 26 A[i],A[r-1]=A[r-1],A[i] 27 return partition(A,p,r) 28 29 A=[2,8,7,1,3,5,6,4] 30 print(randomized_partition(A, 0, 7)) 31 print(A) 32 randomized_quicksort(A,0,7) 33 print(A) 34 ----------------------------------------- 35 3 36 [2, 3, 1, 4, 8, 5, 7, 6] 37 [1, 2, 3, 4, 5, 6, 7, 8]
六.





