树
一.树
1.树是有n个结点的集合,仅有一个根结点,有若干子结点
2.结点拥有的子树数称为结点的度;树的度是树内各结点的度的最大值
3.叶节点(终端节点):度为0的结点;树中还有双亲结点,孩子结点,兄弟结点,子孙结点,祖先结点
4.结点的层数从根开始定义,根为第一层;树中结点的最大层次称为树的深度(高度)
5.森林是互不相交的树的结合
6.树中:结点总数=所有节点度数+1
二.二叉树
1.二叉树:每个结点至多只有两颗子树(即二叉树中不存在度大于2的结点),子树有左右之分,次序不能颠倒
2.性质:
(1)树的结点编号一般是按先序遍历(先根遍历)(一层一层编号)
(2)在二叉树的第 i 层至多有 2i-1 个结点(i>=1)
(3)高度为 k 的二叉树至多有 2k-1 个结点
(4)若叶子结点有 n0 个,度为 2 的结点有 n2 个,则 n0 = n2 +1
(5)一般来说,对于第 i 个结点,它的父亲结点为第 [i/2] 个结点,它左孩子为第 2i 个结点,它的右孩子为第 2i+1 个结点
3.满二叉树:树中每层必须满,共有 2k-1 个结点
4.完全二叉树:(满二叉树砍掉一些树)每个结点都有与其对应的满二叉树中编号为1...n的结点一一对应
(1)具有 n 个结点的完全二叉树的高度为 [log2n]+1
(2)度为1的结点至多为1
5.平衡二叉树(AVL):树中任一结点的左子树和右子树深度之差不超过1
三.二叉搜索树(二叉排序树)(和快速排序非常相似的算法)
1.二叉搜索树:对于任何结点,它的左子树所有结点关键字 <= 该结点关键字 <= 它的右子树所有结点关键字
2.对于一棵二叉搜索树,通过中序遍历(子树根结点关键字位于左子树关键字和右子树关键字之间),可以按序输出所有关键字
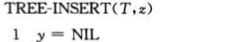
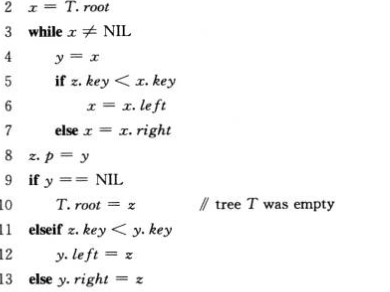



1 class Node: 2 def __init__(self, key, right, left, p): 3 '''节点(关键字,左孩子,右孩子,父节点)''' 4 self.key = key 5 self.right = right 6 self.left = left 7 self.p = p 8 9 class Binary_search_tree: 10 '''二叉搜索树''' 11 def __init__(self, root): 12 '''以根节点初始化一棵树''' 13 self.root = root 14 def tree_insert(self, z): 15 '''在树中插入节点''' 16 y = None 17 x = self.root 18 while x != None: 19 y = x 20 if z.key < x.key: 21 x = x.left 22 else: 23 x = x.right 24 z.p = y 25 if y == None: 26 self.root = z 27 elif z.key < y.key: 28 y.left = z 29 else: 30 y.right = z 31 32 def inorder_tree_walk(self, x): 33 '''中序遍历''' 34 if x != None: 35 self.inorder_tree_walk(x.left) 36 print(x.key) 37 self.inorder_tree_walk(x.right) 38 39 root=Node(6,None,None,None) 40 tree=Binary_search_tree(root) 41 List=[5,2,5,7,8] 42 for i in List: 43 node=Node(i,None,None,None) 44 tree.tree_insert(node) 45 print(tree) 46 print(tree.inorder_tree_walk(tree.root)) 47 ------------------------------------------------------- 48 <__main__.Binary_search_tree object at 0x032B7890> 49 2 50 5 51 5 52 6 53 7 54 8 55 None
3.查询二叉搜索树

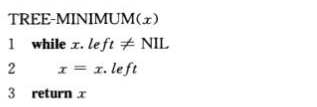



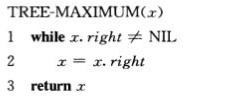

1 def tree_search(tree, x, k): 2 '''查找一个具有给定关键字的节点,x表示指向树根的指针''' 3 if x == None or k == x.key: 4 return x 5 if k < x.key: 6 return tree_search(tree,x.left, k) 7 else: 8 return tree_search(tree,x.right, k) 9 10 def iterative_tree_search(tree, x, k): 11 '''迭代的树的搜索''' 12 while x != None and k != x.key: 13 if k < x.key: 14 x = x.left 15 else: 16 x = x.right 17 return x 18 19 def tree_minimum(tree, x): 20 '''最小关键字元素,最左边的节点''' 21 while x.left != None: 22 x = x.left 23 return x 24 25 def tree_maximum(tree, x): 26 '''最大关键字元素,最右边的节点''' 27 while x.right != None: 28 x = x.right 29 return x 30 31 def tree_successor(tree, x): 32 '''树的前继''' 33 if x.right != None: 34 return tree_minimum(tree,x.right) 35 y = x.p 36 while y != None and x == y.right: 37 x = y 38 y = y.p 39 return y 40 41 root=Node(15,None,None,None) 42 tree=Binary_search_tree(root) 43 List=[6,18,3,7,17,20,2,4,13,9] 44 for i in List: 45 node=Node(i,None,None,None) 46 tree.tree_insert(node) 47 print(tree) 48 print(tree_search(tree, root, 13).key) 49 print(tree_maximum(tree,root).key) 50 print(tree_minimum(tree,root).key) 51 print(tree_successor(tree,tree_search(tree, root, 13)).key) 52 --------------------------------------------------------------------- 53 <__main__.Binary_search_tree object at 0x0391B530> 54 13 55 20 56 2 57 15
4.插入和删除节点
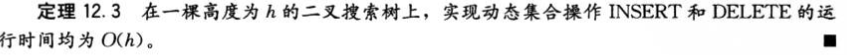


1 def tree_delete(tree, z): 2 '''树的删除节点,分情况讨论''' 3 if z.left == None: 4 #1.z没有左孩子节点,用右孩子来替代他 5 transplant(tree,z, z.right) 6 elif z.right == None: 7 #2.若z没有右孩子,用他的左孩子来替代他 8 transplant(tree,z, z.left) 9 else: 10 #如果有两个孩子,在z的右子树中找他的后继(最小关键字),并让y替代z的位置 11 y = tree_minimum(tree,z.right) 12 if y.p != z: 13 #若y不是z的左孩子,用y右孩子替换y并成为y的双亲的一个孩子,再将z的右孩子转换为y的右孩子 14 transplant(tree,y, y.right) 15 y.right = z.right 16 y.right.p = y 17 #用y替换z并成为z的双亲的一个孩子,再用z的左孩子替换为y的左孩子 18 transplant(tree,z, y) 19 y.left = z.left 20 y.left.p = y 21 22 def transplant(tree, u, v): 23 '''删除u后,树的替代,以一棵v为根的子树来替换一棵u为根的子树 24 结果:u的双亲变为v的双亲,v成为u的双亲的相应孩子''' 25 if u.p == None: 26 #1.若u是根节点,直接初始化一个v为根节点的树 27 tree.root = v 28 elif u == u.p.left: 29 #2.若u是他父节点的左孩子,更新他父节点的左孩子为v 30 u.p.left = v 31 else: 32 #3.若u是他父节点的右孩子,更新他父节点的右孩子为v 33 u.p.right = v 34 if v != None: 35 #如果v不为空,u的父节点变为v的父节点 36 v.p = u.p 37 38 root=Node(15,None,None,None) 39 tree=Binary_search_tree(root) 40 List=[6,18,3,7,17,20,2,4,13,9] 41 for i in List: 42 node=Node(i,None,None,None) 43 tree.tree_insert(node) 44 45 print(tree.inorder_tree_walk(tree.root)) 46 print('#'*30) 47 tree_delete(tree,tree_search(tree, root, 13)) 48 print(tree.inorder_tree_walk(tree.root)) 49 ------------------------------------------------------------------------ 50 2 51 3 52 4 53 6 54 7 55 9 56 13 57 15 58 17 59 18 60 20 61 None 62 ############################## 63 2 64 3 65 4 66 6 67 7 68 9 69 15 70 17 71 18 72 20 73 None
5.随机构建二叉搜索树(参考随机化快速排序)
六.红黑树
1.红黑树是一种确保拥有对数阶O(lg n)高度的二叉搜索树

2.红黑树任何路径只能是红黑红的间隔或连续的黑色,不可能是连续红红

3.黑高:从某个结点出发(不含该结点)到达一个叶结点的的任意一条简单路径上的黑色结点个数,称为该结点的黑高
4.
5.旋转
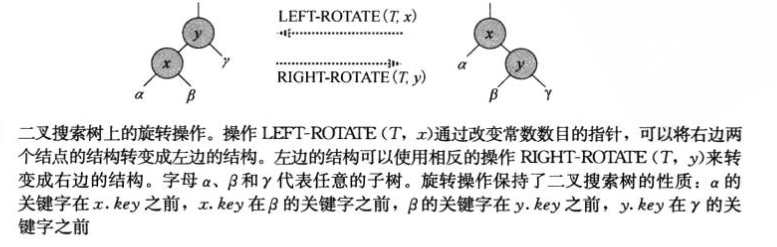
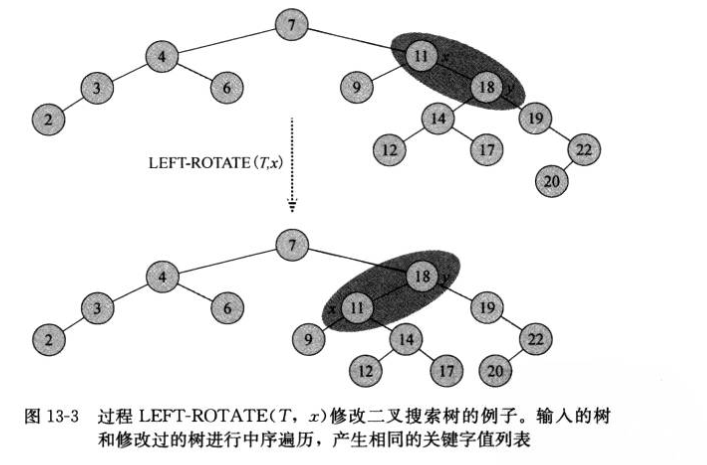

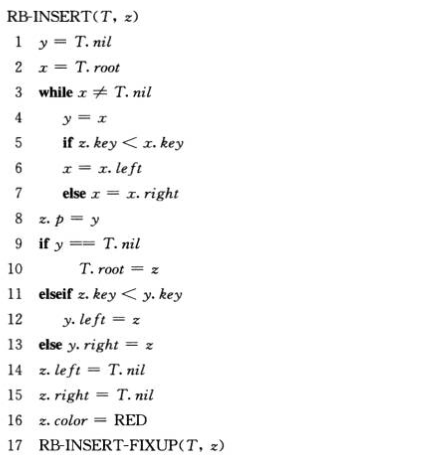



1 class Node: 2 def __init__(self, key, right, left, p, color): 3 self.key = key 4 self.right = right 5 self.left = left 6 self.p = p 7 self.color = color 8 9 class RB_tree: 10 '''红黑树''' 11 def __init__(self, root, nil): 12 self.root = root 13 self.nil = nil 14 15 def tree_insert(self, z): 16 '''树的插入''' 17 y = self.nil 18 x = self.root 19 while x != self.nil: 20 y = x 21 if z.key < x.key: 22 x = x.left 23 else: 24 x = x.right 25 z.p = y 26 if y == self.nil: 27 self.root = z 28 elif z.key < y.key: 29 y.left = z 30 else: 31 y.right = z 32 z.left = self.nil 33 z.right = self.nil 34 z.color = "RED" 35 self.rb_insert_fixup(z) 36 37 def left_rotate(self, x): 38 '''左旋:y是x的右孩子,y变为x和y原来右子树的父节点,x变为x原来左子树和y左子树的父节点''' 39 y = x.right 40 x.right = y.left 41 if y.left != self.nil: 42 y.left.p = x 43 y.p = x.p 44 if x.p == self.nil: 45 self.root = y 46 elif x == x.p.left: 47 x.p.left = y 48 else: 49 x.p.right = y 50 y.left = x 51 x.p = y 52 53 def right_rotate(self, y): 54 '''右旋:x是y的左孩子,x为x原左孩子和y的父节点,y为x原右孩子和y右孩子的父节点''' 55 x = y.left 56 y.left = x.right 57 if x.right != self.nil: 58 x.right.p = y 59 x.p = y.p 60 if y.p == self.nil: 61 self.root = x 62 elif y == y.p.left: 63 y.p.left = x 64 else: 65 y.p.right = x 66 x.right = y 67 y.p = x 68 69 def rb_insert_fixup(self, z): 70 while z.p.color == "RED": 71 if z.p == z.p.p.left: 72 y = z.p.p.right 73 if y.color == "RED": 74 z.p.color = "BLACK" 75 y.color = "BLACK" 76 z.p.p.color = "RED" 77 z = z.p.p 78 else: 79 if z == z.p.right: 80 z = z.p 81 self.left_rotate(z) 82 z.p.color = "BLACK" 83 z.p.p.color = "RED" 84 self.right_rotate(z.p.p) 85 else: 86 y = z.p.p.left 87 if y.color == "RED": 88 z.p.color = "BLACK" 89 y.color = "BLACK" 90 z.p.p.color = "RED" 91 z = z.p.p 92 else: 93 if z == z.p.left: 94 z = z.p 95 self.right_rotate(z) 96 z.p.color = "BLACK" 97 z.p.p.color = "RED" 98 self.left_rotate(z.p.p) 99 self.root.color = "BLACK" 100 101 def inorder_tree_walk(self, x): 102 if x != self.nil: 103 self.inorder_tree_walk(x.left) 104 print(x.key) 105 self.inorder_tree_walk(x.right) 106 107 def tree_search(self, x, k): 108 if x == self.nil or k == x.key: 109 return x 110 if k < x.key: 111 return self.tree_search(x.left, k) 112 else: 113 return self.tree_search(x.right, k) 114 115 116 nil=Node(0,None,None,None,"BLACK")#哨兵节点,黑色 117 root=Node(7,nil,nil,nil,"BLACK")#根节点,黑色 118 t=RB_tree(root,nil) 119 T=[4,18,3,6,11,19,2,9,14,22,12,17,20] 120 for i in T: 121 z=Node(i,None,None,None,"RED") 122 t.tree_insert(z) 123 TT=[7,4,18,3,6,11,19,2,9,14,22,12,17,20] 124 for i in TT: 125 zz=t.tree_search(t.root,i) 126 print(i,' ',zz.color) 127 ------------------------------------------- 128 7 BLACK 129 4 BLACK 130 18 BLACK 131 3 BLACK 132 6 BLACK 133 11 RED 134 19 RED 135 2 RED 136 9 BLACK 137 14 BLACK 138 22 RED 139 12 RED 140 17 RED 141 20 BLACK
删除
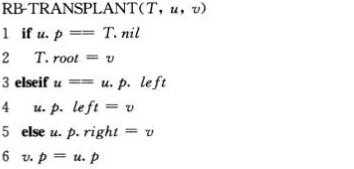



1 def rb_transplant(self, u, v): 2 if u.p == self.nil: 3 self.root = v 4 elif u == u.p.left: 5 u.p.left = v 6 else: 7 u.p.right = v 8 v.p = u.p 9 10 def tree_minimum(self, x): 11 while x.left != self.nil: 12 x = x.left 13 return x 14 15 def rb_delete(self, z): 16 y = z 17 y_original_color = y.color 18 if z.left == self.nil: 19 x = z.right 20 self.rb_transplant(z, z.right) 21 elif z.right == self.nil: 22 x = z.left 23 self.rb_transplant(z, z.left) 24 else: 25 y = self.tree_minimum(z.right) 26 y_original_color = y.color 27 x = y.right 28 if y.p == z: 29 x.p = y 30 else: 31 self.rb_transplant(y, y.right) 32 y.right = z.right 33 y.right.p = y 34 self.rb_transplant(z, y) 35 y.left = z.left 36 y.left.p = y 37 y.color = z.color 38 if y_original_color == "BLACK": 39 self.rb_delete_fixup(x) 40 41 def rb_delete_fixup(self, x): 42 while x != self.root and x.color == "BLACK": 43 if x == x.p.left: 44 w = x.p.right 45 if w.color == "RED": 46 w.color = "BLACK" 47 x.p.color = "RED" 48 self.left_rotate(x.p) 49 w = x.p.right 50 if w.left.color == "BLACK" and w.right.color == "BLACK": 51 w.color = "RED" 52 x = x.p 53 else: 54 if w.right.color == "BLACK": 55 w.left.color == "BLACK" 56 w.color = "RED" 57 self.right_rotate(w) 58 w = x.p.right 59 w.color = x.p.color 60 x.p.color = "BLACK" 61 w.right.color = "BLACK" 62 self.left_rotate(x.p) 63 x = self.root 64 else: 65 w = x.p.left 66 if w.color == "RED": 67 w.color = "BLACK" 68 x.p.color = "RED" 69 self.right_rotate(x.p) 70 w = x.p.left 71 if w.right.color == "BLACK" and w.left.color == "BLACK": 72 w.color = "RED" 73 x = x.p 74 else: 75 if w.left.color == "BLACK": 76 w.right.color == "BLACK" 77 w.color = "RED" 78 self.left_rotate(w) 79 w = x.p.left 80 w.color = x.p.color 81 x.p.color = "BLACK" 82 w.left.color = "BLACK" 83 self.right_rotate(x.p) 84 x = self.root 85 x.color = "BLACK"




