哈希表

一.符号表问题

1.一个表里面放着n条记录，（记录x：x通常是一个指向实际数据的指针）

2.在每个记录中，存在一个记录的键，还存在一些卫星数据（属于键的附加数据）

3.排序是对记录进行排序，而不是关键字

4.对表进行操作：添加记录，删除记录，查找具有特定键的记录

 

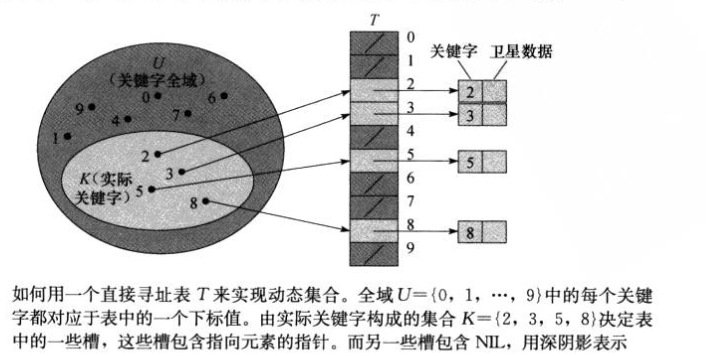
二.直接映射表（数组）

1.适用于关键字的全域（可能存储的关键字）较小的情况

2.数组的每个位置对应全域中的一个关键字，关键字k的元素被存放在槽k中  

3.缺陷：如果关键字只有几千，而关键字的全域需64位来表示，导致大量空槽

class direct_address_table:
    '''直接寻址表'''
    def __init__(self, T=[], size=0):
        if len(T) == 0:
            self.T = [None for i in range(size)]
        else:
            self.T = T
        self.size = size
    '''对于节点'''
    def search(self, k):
        return self.T[k]

    def insert(self, x):
        self.T[x.key] = x

    def delete(self, x):
        self.T[x.key] = None

class Node:
    def __init__(self, key):
        self.key = key

T=[]
dat=direct_address_table(T,10)
x=Node(2)
print(dat.insert(x))

 

三.哈希表（散列表）（Hash Table）（一个长度与实际存储关键字数目成比例的数组）

1.哈希法：用一个hash函数来随机映射那些键到哈希表T的槽

2.哈希表是一种根据关键字，计算相应的存储位置，访问数据的数据结构，

3.适用于：实际存储的关键字数目比全部的可能关键字总数较少时

4.利用哈希函数（hash function）h，把原来具有关键字k的元素存放在槽k中变成该元素放在h(k)中

 

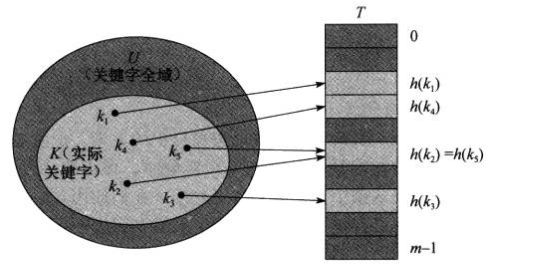
三.哈希函数

一个好的哈希函数：每个关键字都被等可能地哈希到m个槽位中的任何一个，并与其他关键字已散列到哪个槽位无关

（1）除法散列法：用一个特定的素数m来除所给的关键字，h(k)=k mod m ，k为关键字，m为散列表大小而且不能太小,m一般不为2的幂或10的幂等相似的

（2）乘法散列法：对m的选择不是特别关键，一般为2的幂，A不要太接近以2为底的数

（3）全域散列法：从一组精心设计的函数中，随机地选择一个作为散列函数，使之独立于要存储的关键字

 

三.冲突：多个关键字映射到数组的同一下标

 解决冲突：

（1）链接法：把相同的哈希值的记录放到一个链表里存储

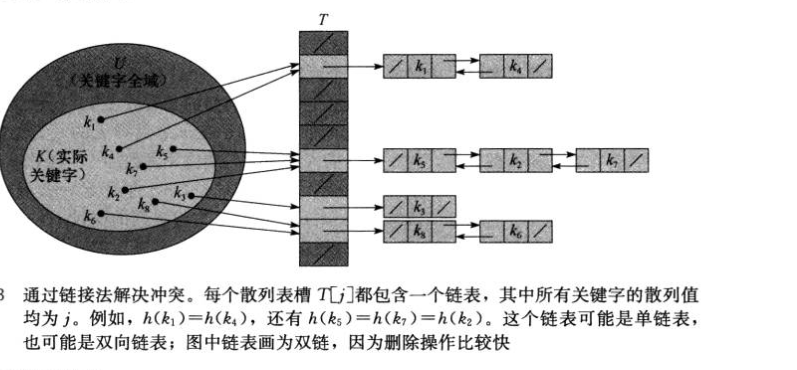
最坏情况分析：所有键映射到同一个槽，访问θ（n）

平均情况分析：假设简单均匀哈希（每个属于集合的键都有相同的几率被哈希映射到表的任意一个槽中），每个键与其他的键相互独立

 

1是把键只哈希映射到槽所需要的时间，α是搜索槽对应的链表所花费的时间

class chained_hash:
    '''链接法散列，查找和插入时都要判断槽中有没有元素'''
    def __init__(self, T=[], size=0):
        if len(T) == 0:
            self.T = [None for i in range(size)]
        else:
            self.T = T
        self.size = size
    def search(self, k):
        if self.T[self.hash_h(k)] != None:
            x = self.T[self.hash_h(k)].list_search(k)
            return x
        return None
    def insert(self, x):
        if self.T[self.hash_h(x.key)] == None:
            self.T[self.hash_h(x.key)] = DoublyLinkedList(x)
        else:
            self.T[self.hash_h(x.key)].list_insert(x)
    def delete(self, x):
        self.T[self.hash_h(x.key)].list_delete(x)
    def hash_h(self, key):
        '''hash函数'''
        return key % 12

class Node:
    def __init__(self, key):
        self.key = key
class DoublyNode:
    def __init__(self, n_prev, n_next, key):
        self.prev = n_prev
        self.next = n_next
        self.key = key

class DoublyLinkedList:
    def __init__(self, head):
        self.head = head

    def list_search(self, k):
        x = self.head
        while x != None and x.key != k:
            x = x.next
        return x

    def list_insert(self, x):
        x.next = self.head
        if self.head != None:
            self.head.prev = x
        self.head = x
        x.prev = None

    def list_delete(self, x):
        if x.prev != None:
            x.prev.next = x.next
        else:
            self.head = x.next
        if x.next != None:
            x.next.prev = x.prev

T=[]
x=DoublyNode(None,None,13)
ch=chained_hash(T,12)
ch.insert(x)
x=DoublyNode(None,None,25)
ch.insert(x)
y=ch.search(25)
print(y.key)

ch.delete(y)
print(ch.T[1].head)
print(ch.T[1].head.key)
print(ch.T[1].head.next)
-----------------------------------------
25
<__main__.DoublyNode object at 0x039C78B0>
13
None

（2）开放寻址法：所有元素都存放在散列表中，系统地探查哈希表直到找到空槽

探查：连续地检查散列表，来找到空槽放置待插入的关键字

计算开放寻址中的探查序列：

（1）线性探查：h(k,i)=(h'(k)+i)mod m ,i=1...m-1

（2）二次探查：h(k,i)=(h'(k)+c1 i+c2 i*2)mod m, 

（3）双重散列：（h1(k)+ih2(k)）mod m 

class open_address_hash:
    '''开放寻址散列，散列表T和一个关键字k'''
    def __init__(self, T=[], size=0):
        if len(T) == 0:
            self.T = [None for i in range(size)]
        else:
            self.T = T
        self.size = size

    def hash_insert(self, k):
        '''插入关键字k，返回k的插槽或已满标志'''
        i = 0
        while i < self.size:
            j = self.hash_h1_h2(k, i)#搜寻空槽并插入
            if self.T[j] == None:
                self.T[j] = k
                return j
            else:
                i += 1
        return "hash table overflow"

    def hash_search(self, k):
        '''查找，如果槽j包含了关键字k，则返回j，否则返回NOne'''
        i = 0
        j = self.hash_h1_h2(k, i)
        while self.T[j] != None and i < self.size:
            j = self.hash_h1_h2(k, i)
            if self.T[j] == k:
                return j
            else:
                i += 1
        return None

    def hash_h1_h2(self, k, i):
        '''hash 函数'''
        return ((k % self.size + i * (1 + k % (self.size - 2)))) % self.size

T=[]
oah=open_address_hash(T,13)
print(oah.hash_insert(79))
print(oah.hash_insert(69))
print(oah.hash_search(50))
------------------------------
1
4
None

 

四.全域哈希和完全哈希

1.哈希的根本缺陷：对任意哈希函数，都存在一个不好的键集，所有键都会哈希映射到同一个槽

2.全域哈希：随机选择哈希函数，使之独立于要存储的关键字