中位数和顺序统计量
一.中位数和顺序统计量
顺序统计量:第i个顺序统计量是该集合中第i小的元素
中位数A[i]:i=[(n+1)/2]
选择问题:在一个包含n个(互异)元素组成的无序集合中,在不排序的情况下,选出第k个顺序统计量
二.选择最大最小值:通过遍历集合每个元素,记录最大最小值。O(n)


1 #最小值和最大值 2 def MINMAX(A): 3 min = A[0] 4 max = A[0] 5 for i in range(1,len(A)): 6 if min>A[i]: 7 min = A[i] 8 if max<A[i]: 9 max = A[i] 10 return (min,max) 11 12 A=[0.78,0.17,0.39,0.26,0.72,0.94,0.21,0.12,0.23,0.68] 13 minimax=MINMAX(A) 14 print(minimax ) 15 --------------------------------------------------- 16 (0.12, 0.94)
三.随机选择算法: 期望为线性时间O(n)


1 import random 2 3 #处理划分的一边,根据快速排序的性质,迅速求得第i顺序统计量 4 def randomized_select(A,p,r,i): 5 if p == r: 6 return A[p] 7 q=randomized_partition(A,p,r) 8 k=q-p+1 9 if i == k: 10 return A[q] 11 elif i<k: 12 return randomized_select(A,p,q-1,i) 13 else: 14 return randomized_select(A,q+1,r,i-k) 15 16 #对输入数组进行递归划分,返回划分下标 17 def randomized_partition(A, p, r): 18 i = random.randint(p, r) 19 A[i], A[r - 1] = A[r - 1], A[i] 20 x = A[r] 21 i = p - 1 22 for j in range(p, r): 23 if A[j] < x: 24 i += 1 25 A[i], A[j] = A[j], A[i] 26 A[r] = A[i + 1] 27 A[i + 1] = x 28 return i + 1 29 30 A=[2,8,7,1,3,5,6,4] 31 print(randomized_select(A, 0, 7, 2)) 32 ------------------------------------------------------------ 33 2
分析:
最好情况最坏划分:1/10-9/10划分,(n)
最坏情况:0-n-1划分,O(n2)
平均情况:

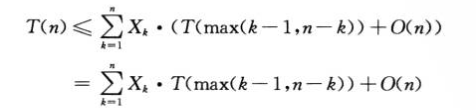
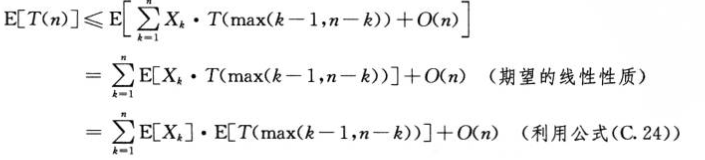
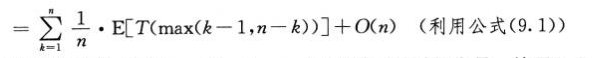
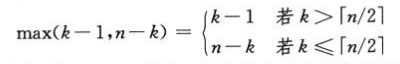
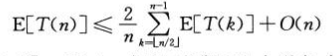
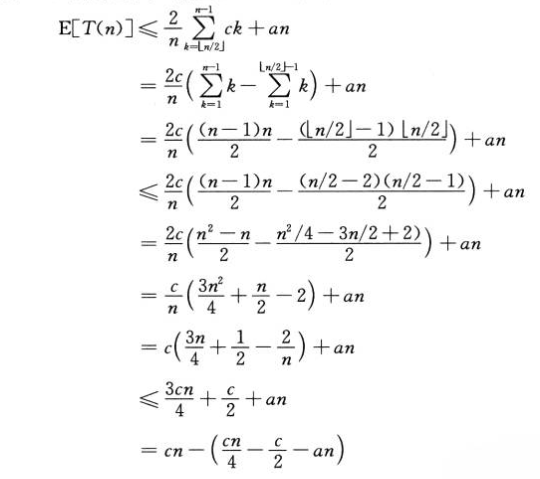
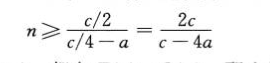
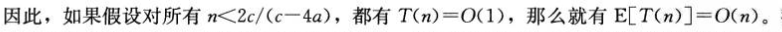
四.最坏情况为线性时间的选择算法