线性时间排序

一.线性时间排序

1.排序算法复杂度都可以是线性时间O（n）

2.都是在一定假设的条件下进行

 

二.计数排序：假设输入的n个数据的每一个都是0-k区间的一个整数，对于一个元素x,确定小于x的元素个数，把x放在对于数组位置

时间复杂度：O(k+n);当k=O(n)时,

#计数排序
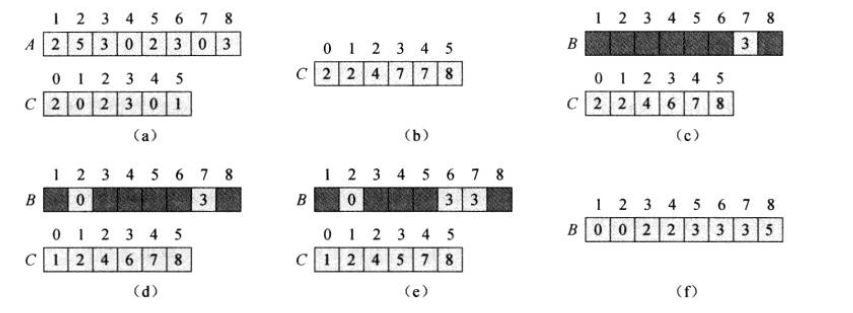
def counting_sort(A,B,k):
    n=len(A)
    C=[]
    for i in range(0,k+1):
        C.append(0)#C全置为0
    for j in range(0,n):
        C[A[j]]=C[A[j]]+1#计算A中每个元素的个数，存放在C中
    for i in range(1,k+1):
        C[i]=C[i]+C[i-1]#总加和
    for j in range(n-1,-1,-1):
        #从后到前，把A[j]放在B的正确位置
        B[C[A[j]]-1]=A[j]
        C[A[j]]=C[A[j]]-1#更新C

A=[2,5,3,0,2,3,0,3]
B=[0,0,0,0,0,0,0,0]
counting_sort(A,B,5)
print(A)
print(B)
----------------------------------------
[2, 5, 3, 0, 2, 3, 0, 3]
[0, 0, 2, 2, 3, 3, 3, 5]

 

二.基数排序：先按最低有效位进行排序，在将所有卡片合成一叠

为了保证计数排序的正确性，一位数排序算法必须是稳定的

 

 

 

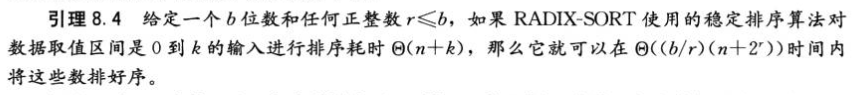
四.桶排序:假设输入数据服从均匀分布，平均情况下它的时间代价为O(n)。将【0,1）区间划分n个相同大小的子区间（桶），对每个桶排序从而实现整个的排序

import math

#桶排序
def bucket_sort(A):
    n = len(A)#实际控制桶的个数
    B = [[] for i in range(n)]
    print(B)#创建空列表B
    for i in range(0, n):
        B[math.floor(n * A[i])].append(A[i])
    print(B)#把A【i】插入B[nA[i]]
    for i in range(0, n):
        insertion_sort(B[i])#对每个B【i】排序
    del A[:]#清空A
    for each in B:
        A.extend(each)#在A中插入已排好的数

#插入排序
def insertion_sort(A):
    for j in range(1, len(A)):
        key = A[j]
        i = j - 1
        while i >= 0 and A[i] > key:
            A[i + 1] = A[i]
            i = i - 1
            A[i + 1] = key

A=[0.78,0.17,0.39,0.26,0.72,0.94,0.21,0.12,0.23,0.68]
bucket_sort(A)
print(A)
--------------------------------------------------------------
[[], [], [], [], [], [], [], [], [], []]
[[], [0.17, 0.12], [0.26, 0.21, 0.23], [0.39], [], [], [0.68], [0.78, 0.72], [], [0.94]]
[0.12, 0.17, 0.21, 0.23, 0.26, 0.39, 0.68, 0.72, 0.78, 0.94]