堆

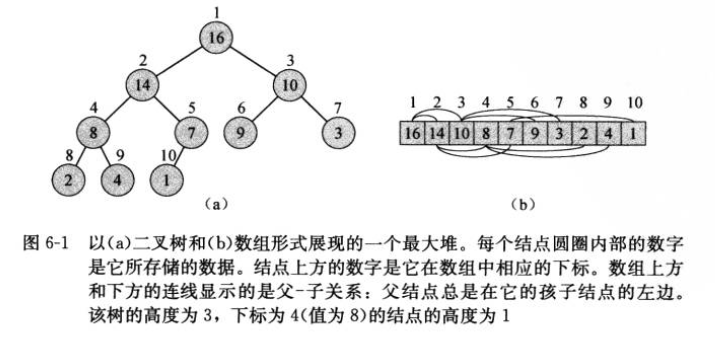



1 import math 2 #定义一个类,堆 3 class heap: 4 def __init__(self,A): 5 self.list=A#堆是由列表得来 6 self.heap_size = len(A)#堆的大小是列表的长度 7 def parent(self,i): 8 #i的父节点 9 return math.floor((i-1)/2) 10 def left(self,i): 11 #i的左节点 12 return 2*i+1 13 def right(self,i): 14 #i的右节点 15 return 2*i+2 16 ------------------------------------------------------ 17 A=[4,1,3,2,16,9,10,14,8,7] 18 H=heap(A) 19 print(H)


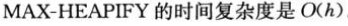 ,h是树高
,h是树高

1 #要求:以list中第i个元素为根节点的子树满足最大堆要求, 2 # 输入一个堆和他的某个元素,返回满足要求的堆的列表形式 3 def max_heapify(H,i): 4 A=H.list 5 largest = i#默认初始最大值的下标为i 6 l = H.left(i)#l是i的左节点下标 7 r = H.right(i)#r是i的右节点下标 8 if l<H.heap_size and A[l] > A[largest]: 9 largest = 2*i+1 10 if r<H.heap_size and A[r] > A[largest]: 11 largest = 2*i+2 12 #从A【i】,A[left(i)],A[right(i)]中选出最大的,将其下标存储在largest中 13 if largest != i: 14 #如果i不是最大的,则交换A[i]和A[largest], 15 #此时下标largest的节点的值是原来的A【i】,对该子树进行递归调用 16 A[i], A[largest] = A[largest], A[i] 17 max_heapify(H,largest) 18 return A 19 20 A=[4,1,3,2,16,9,10,14,8,7] 21 H=heap(A) 22 print(max_heapify(H,0)) 23 ----------------------------------------------- 24 [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]


1 #建立最大堆,输入一个堆,返回满足最大堆的列表 2 def build_max_heap(H): 3 A = H.list 4 N = math.floor(H.heap_size/2)-1 5 #对于每个节点,要求满足最大堆的规则 6 for i in range(N,-1,-1): 7 max_heapify(H,i) 8 return A 9 10 print(build_max_heap(H)) 11 --------------------------------------- 12 [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]


1 #堆排序,输入一个堆,通过迭代建立最大堆并每次取出堆的最大值放在最后面,来从小到大排序 2 def heapsort(H): 3 A = H.list 4 build_max_heap(H) 5 #利用heap_size从堆中去掉节点n 6 for i in range(H.heap_size - 1, 0, -1): 7 A[i],A[0]=A[0],A[i] 8 H.heap_size-=1 9 max_heapify(H, 0) 10 return A 11 print(heapsort(H)) 12 ------------------------------------------------------------ 13 [1, 2, 3, 4, 7, 8, 9, 10, 14, 16]



1 #提取最大堆的最大元素,并且去掉它,再对于其余的进行最大堆化 2 #并没有对他排序,但任然能提取最大元素 3 def heap_extract_max(H): 4 if H.heap_size<1: 5 raise ('heap underflow') 6 A = H.list 7 max=A[0] 8 A[0]=A[H.heap_size-1] 9 H.heap_size-=1 10 max_heapify(H,0) 11 return max 12 A=[4,1,3,2,16,9,10,14,8,7] 13 H=heap(A) 14 p=build_max_heap(H) 15 print(p) 16 B=heap(p) 17 print(heap_extract_max(B)) 18 print(heap_extract_max(B)) 19 print(heap_extract_max(B)) 20 print(heap_extract_max(B)) 21 print(heap_extract_max(B)) 22 ----------------------------------------------------- 23 [16, 14, 10, 8, 7, 9, 3, 2, 4, 1] 24 16 25 14 26 10 27 9 28 8
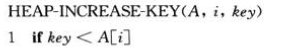


1 #修改某个关键字,把关键字放到合适位置,使他满足最大堆性质 2 def heap_increase_key(A,i,key): 3 H=heap(build_max_heap(heap(A))) 4 if key < A[i]: 5 raise("new key is smaller than current key") 6 A[i]=key 7 while i>0 and A[H.parent(i)]<A[i]: 8 A[i],A[H.parent(i)]=A[H.parent(i)],A[i] 9 i=H.parent(i) 10 11 A=[4,1,3,2,16,9,10,14,8,7] 12 print(A) 13 heap_increase_key(A,8,15) 14 print(A) 15 ------------------------------------------------------------ 16 [4, 1, 3, 2, 16, 9, 10, 14, 8, 7] 17 [16, 15, 10, 14, 7, 9, 3, 2, 8, 1]


1 #他的输入是要被插入到最大堆中的新元素的关键字 2 def max_heap_insert(A,key): 3 A.append(float("-inf")) 4 heap_increase_key(A,len(A)-1,key) 5 6 7 A=[4,1,3,2,16,9,10,14,8,7] 8 print(A) 9 max_heap_insert(A,13) 10 print(A) 11 ----------------------------------------------- 12 [4, 1, 3, 2, 16, 9, 10, 14, 8, 7] 13 [16, 14, 10, 8, 13, 9, 3, 2, 4, 1, 7]






