贪心算法
一.贪心算法
1.总是做出局部最优解,寄希望这样的选择能导致全局最优解,即每一步都做出当时看起来最佳的选择,
2.贪心算法并不保证得到最优解,但对很多问题可以求得最优解
3. 对于一个问题,可能有多种贪心策略
4.贪心算法通常自顶向下地设计,做出一个选择,然后求解剩下的那个子问题,而不是自底向上地求解更多的子问题然后再做出选择
5.一般步骤:

6.证明一个贪心算法能否求解一个最优化问题的两个关键要素
(1)贪心选择性质:每步的贪心选择都是当时的最优解,贪心算法进行选择时可能依赖之前作出的选择,但不依赖任何将来的选择或是子问题的解,而且第一次选择之前不求解任何子问题
(2)最优子结构:原问题最优解包含其子问题的最优解
二.活动选择问题
1.问题描述:

2.最优子结构:可证明:原问题最优解必然包含子问题的最优解
3.一种贪心选择:选择一个活动使选出他后剩下的资源能尽量多
4.递归贪心算法:


1 #递归贪心活动选择 2 def recursive_activity_selector(s,f,k,n): 3 #s活动开始时间,f活动结束时间,k代表子问题的下标,n问题规模 4 m=k+1#假设已知Sk的最优解,递归求解Sn的最优解 5 while m<=n and s[m]<f[k]: 6 m=m+1 7 if m<=n: 8 return str(m)+" "+str(recursive_activity_selector(s,f,m,n)) 9 else: 10 return " " 11 12 13 f=[0,4,5,6,7,9,9,10,11,12,14,16] 14 s=[0,1,3,0,5,3,5,6,8,8,2,12] 15 n=11 16 k=0 17 print(recursive_activity_selector(s,f,k,n)) 18 ---------------------------------------------------- 19 1 4 8 11
5.迭代贪心算法:尾递归:以一个对自身的递归调用再接一次并集操作结尾
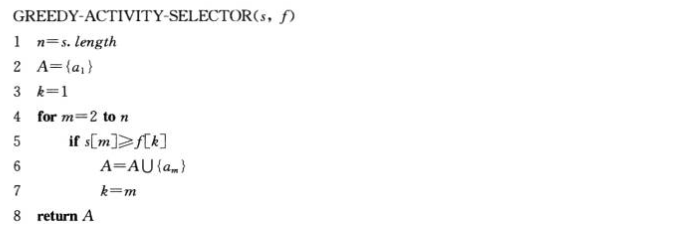

1 #迭代求解 2 def greedy_activity_selector(s,f): 3 #s活动开始时间,f活动结束时间 4 n=len(s)-1 5 A=[]#选出的活动集合 6 A.append(1) 7 #已假定输入活动已按结束时间单调递增排好序 8 k=1 9 for m in range(2,n+1): 10 if s[m]>=f[k]:#k表示最后选择的活动,m表示对比的活动 11 A.append(m) 12 k=m 13 return A 14 15 s=[0,1,3,0,5,3,5,6,8,8,2,12] 16 f=[0,4,5,6,7,9,9,10,11,12,14,16] 17 print(greedy_activity_selector(s, f)) 18 ------------------------------------------------------------ 19 [1, 4, 8, 11]
三.赫夫曼编码
1.前提:(1)编码(二进制编码):把字符根据某种策略转换为计算机能识别的二进制形式(2)码字:每个字符用一个唯一的二进制串表示
(3)定长编码:所有字符的二进制编码长度一样(4)变长编码:赋予高频字符短码字,低频字符长码字,一般可达到比定长编码更好的压缩率
(5)前缀码:没有任何码字是其他码字的前缀,用来简化解码,保证达到最优数据压缩率
(6)满二叉树:每个非叶节点都有两个孩子节点
2.赫夫曼编码:通过二叉树的结构,其叶节点为给定的字符,字符的二进制码字用从根节点(最高频字符)到该字符的叶节点的简单路径表示,0转向左孩子,1转向右孩子,最优的编码方式总是对应一棵满二叉树
3.问题描述:设计一个贪心算法来构造最优前缀码
4.赫夫曼算法具有最优子结构和贪心选择性



1 from heapq import heapify, heappush, heappop 2 from itertools import count 3 4 #借助堆来表达二叉树,先弹出原先两个最小频率的节点,合并成一个新节点并重新插入到堆 5 def huffman(seq, frq): 6 #seq字符集,frq每个字符对应的频率 7 num = count()#统计函数,从0开始 8 trees = list(zip(frq, num, seq)) # num确保有序排列 9 # [(5, 0, 'f'), (9, 1, 'e'), (12, 2, 'c'), (13, 3, 'b'), (16, 4, 'd'), (45, 5, 'a')] 10 heapify(trees) # 把列表转化成小顶堆,节点(关键字,属性,属性) 11 print(trees) 12 while len(trees) > 1: 13 fa, _, a = heappop(trees) # 默认先把列表变成小顶堆的结构,再弹出顶部最小元素(frq,num,seq) 14 fb, _, b = heappop(trees) 15 n = next(num)#统计函数的值+1 16 heappush(trees, (fa + fb, n, [a, b])) # 默认先把列表变成小顶堆的结构,再往堆中插入原先最小两个值的和 17 print(trees) 18 return trees[0][-1] 19 20 seq = 'fecbda' 21 frq = [5,9,12,13,16,45] 22 print(huffman(seq, frq)) 23 -------------------------------------------------- 24 [(5, 0, 'f'), (9, 1, 'e'), (12, 2, 'c'), (13, 3, 'b'), (16, 4, 'd'), (45, 5, 'a')] 25 [(100, 10, ['a', [['c', 'b'], [['f', 'e'], 'd']]])] 26 ['a', [['c', 'b'], [['f', 'e'], 'd']]]
四.拟阵
1.定义

序偶M:两个具有固定次序的客体组成一个序偶,它常常表达两个客体之间的关系。
I(1)非空族:非空的(子集的集合)(2)遗传性:如果一个集合B属于I,则它的所有子集也属于I
交换性:在I中,只要一个独立子集不是最大的(元素最多),我们总可以找到比它大一点的独立子集
2.图拟阵:如果图G=(V,E)是一个无向图,那么M(G)=(S(G),I(G))是一个拟阵,其中S(G)=E是一个有限集,而且I(G)是它的非空族
3.对于A∈I和一个元素x不∈A,如果A∪{x}属于I,则x是A的一个拓展。如果一个独立子集不存在拓展,则称它是最大的。
4.拟阵中所有最大独立子集都具有相同大小
5.加权拟阵:





1 def greedy(E, S, w): 2 A = [] #累积集合A,初始为空,终止为最大独立子集 3 for e in sorted(E, key=w): #按权重单调递减的顺序考虑每个在S中的元素 4 TT = A + [e] 5 if TT in S: #如果A∪{x}是独立的,就将e加到累积集合A中 6 A = TT 7 return A
6.拟阵具有贪心选择性质和最优子结构性质
6.拟阵理论不能完全覆盖所有的贪心算法(如赫夫曼编码问题),但它可以覆盖大多数具有实际意义的情况
五.贪心法对比动态规划
1.相同:都利用了最优子结构,都一般用于求解最优化问题
2.不同:
(1)贪心法:第一次选择之前不求解任何子问题;贪心选择后只留下唯一一个子问题;贪心算法进行选择时可能依赖之前作出的选择,但不依赖任何将来的选择或是子问题的解;一般自顶向下迭代求解;原问题最优解就是把子问题最优解和贪心选择组合起来
(2)动态规划:先求解子问题才能进行第一次选择;一次选择后可能有多个子问题;子问题有重叠性;一般自底向上带备忘地递归求解;原问题的最优解是根据计算出的子问题最优解构造出来的
比如:

分析:这两个问题都有最优子结构,但分数背包问题能用贪心法,而0-1背包问题不能,
原因在于0-1问题将一个商品装到背包时,必须比较包含此商品的子问题的解与不包含它的子问题的解,然后才能做出选择,这会导致大量的重叠子问题




