算法 准备

一.算法

1.算法：算法面向一个问题，体现解决问题的流程，问题定义输入和输出的关系，

2.特点：有穷性、确定性、能行性、输入、输出

 

二.算法设计和分析

1.算法一般用伪代码描述，重点体现流程

2.算法的运行时间：

（1）考虑输入的情况，相同规模不同的输入可能导致算法的运行时间不同，比如顺序和逆序的排序

（2）考虑输入的规模，一般来说，输入规模越大，算法运行时间越长，比如排序6个元素和6万个元素

（3）考虑到算法运行时间的上界，一般来说，对别人说某个算法的运行时间，只会给出最多运行多少时间，不会给出最少运行时间，因为算法注重的是效率

（4）考虑到算法在不同机器上的运行速度不同，一般假设算法在相同机器上的运行，也就是不考虑机器对算法的影响，也被称为相对运行速度

3.分析算法：一般考虑规模为n的算法的最坏运行时间的相对运行时间

（1）算法的最坏运行时间（通常考虑）：最长运行时间，也就是任何输入的运行时间的一个上界

（2）算法的平均运行时间（偶尔考虑）：所有可能输入的加权平均期望时间，必须先知道输入的统计分布

（3）算法的最好运行时间（一般不考虑）：是虚假的，具有欺骗性的数据，因为不会每次都能达到最好的输入，

4.分析算法的一般方法是渐近分析：（1）忽略低阶项和常系数（2）对于输入规模n的算法只考虑算法的运行时间的增长率或增长量级

 

三.渐近分析

1.典型的增长阶：

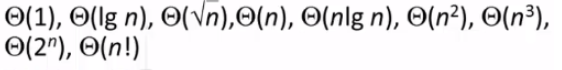
2.增长的记号：

 

3.

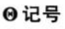^{=（渐近紧界）}

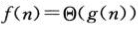，f(n)等于theta(g(n))（f(n)属于theta(g(n))函数集的集合）

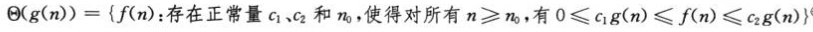
 例：θ（n²）<θ（n³）表示当n>某个n0时，前者的性能好于后者

 

4.

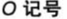^{<=（最坏运行时间）（渐近上界）}

例1：2n²=O(n³)等价于2n²属于O(n³)的集合

例2：f(n)=n³+O(n²)表示存在h(n)属于O(n²)，使得f(n)=n³+h(n)

例3：n²+O(n)=O(n²)表示对于任意f(n)属于O(n)，存在h(n)属于O(n²)，使得n²+f(n)=h(n)

 

5. 

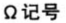^{>=(渐近下界)}

 

6.< 和 >