20172313 2018-2019-1 《程序设计与数据结构》课堂测试修改报告
20172313 2018-2019-1 《程序设计与数据结构》课堂测试修改报告
课程:《程序设计与数据结构》
班级: 1723
姓名: 余坤澎
学号:20172313
实验教师:王志强
实验日期:2018年10月19日
必修/选修: 必修
题目内容

测试原理
- 顺序查找:原理较为简单,通过遍历列表逐个比较进行查找。
- 折半查找:首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
- 哈希查找(散列查找):
- 概念理解:什么是哈希查找呢?在弄清楚什么是哈希查找之前,我们要弄清楚哈希技术,哈希技术是在记录的存储位置和记录的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。查找时,根据这个确定的对应关系找到给定值的映射f(key),若查找集合中存在这个记录,则必定在f(key)的位置上。哈希技术既是一种存储方法,也是一种查找方法。
- 哈希函数大体有六种构造方法:
1,直接定址法:
函数公式:f(key)=a*key+b (a,b为常数)
这种方法的优点是:简单,均匀,不会产生冲突。但是需要事先知道关键字的分布情况,适合查找表较小并且连续的情况。
2,数字分析法:
比如我们的11位手机号码“136XXXX7887”,其中前三位是接入号,一般对应不同运营公司的子品牌,如130是联通如意通,136是移动神州行,153是电信等。中间四们是HLR识别号,表示用户归属地。最后四们才是真正的用户号。
若我们现在要存储某家公司员工登记表,如果用手机号码作为关键字,那么极有可能前7位都是相同的,所以我们选择后面的四们作为哈希地址就是不错的选择。
3,平方取中法:
故名思义,比如关键字是1234,那么它的平方就是1522756,再抽取中间的3位就是227作为哈希地址。
4,折叠法:
折叠法是将关键字从左到右分割成位数相等的几个部分(最后一部分位数不够可以短些),然后将这几部分叠加求和,并按哈希表表长,取后几位作为哈希地址。
比如我们的关键字是9876543210,哈希表表长三位,我们将它分为四组,987|654|321|0 ,然后将它们叠加求和987+654+321+0=1962,再求后3位即得到哈希地址为962,哈哈,是不是很有意思。
5,除留余数法:
函数公式:f(key)=key mod p (p<=m)m为哈希表表长。
这种方法是最常用的哈希函数构造方法。
6,随机数法:
函数公式:f(key)= random(key)。
这里random是随机函数,当关键字的长度不等是,采用这种方法比较合适。- 冲突的产生:两个不同的的关键字可能对应同一个内存地址。 这样,将导致后方的关键字无法储存。
- 冲突的解决:
- 开放定值法:这种方法也称再散列法,其基本思想是:当关键字key的哈希地址p=H(key)出现冲突时,以p为基础,产生另一个哈希地址p1,如果p1仍然冲突,再以p为基础,产生另一个哈希地址p2,…,直到找出一个不冲突的哈希地址pi ,将相应元素存入其中。这种方法有一个通用的再散列函数形式:
Hi=(H(key)+di)% m i=1,2,…,n
其中H(key)为哈希函数,m 为表长,di称为增量序列。增量序列的取值方式不同,相应的再散列方式也不同。主要有以下三种:
- 开放定值法:这种方法也称再散列法,其基本思想是:当关键字key的哈希地址p=H(key)出现冲突时,以p为基础,产生另一个哈希地址p1,如果p1仍然冲突,再以p为基础,产生另一个哈希地址p2,…,直到找出一个不冲突的哈希地址pi ,将相应元素存入其中。这种方法有一个通用的再散列函数形式:
线性探测再散列
dii=1,2,3,…,m-1
这种方法的特点是:冲突发生时,顺序查看表中下一单元,直到找出一个空单元或查遍全表。
二次探测再散列
di=12,-12,22,-22,…,k2,-k2 ( k<=m/2 )
这种方法的特点是:冲突发生时,在表的左右进行跳跃式探测,比较灵活。
伪随机探测再散列
di=伪随机数序列。
具体实现时,应建立一个伪随机数发生器,(如i=(i+p) % m),并给定一个随机数做起点。
例如,已知哈希表长度m=11,哈希函数为:H(key)= key % 11,则H(47)=3,H(26)=4,H(60)=5,假设下一个关键字为69,则H(69)=3,与47冲突。
如果用线性探测再散列处理冲突,下一个哈希地址为H1=(3 + 1)% 11 = 4,仍然冲突,再找下一个哈希地址为H2=(3 + 2)% 11 = 5,还是冲突,继续找下一个哈希地址为H3=(3 + 3)% 11 = 6,此时不再冲突,将69填入5号单元。
如果用二次探测再散列处理冲突,下一个哈希地址为H1=(3 + 12)% 11 = 4,仍然冲突,再找下一个哈希地址为H2=(3 - 12)% 11 = 2,此时不再冲突,将69填入2号单元。
如果用伪随机探测再散列处理冲突,且伪随机数序列为:2,5,9,……..,则下一个哈希地址为H1=(3 + 2)% 11 = 5,仍然冲突,再找下一个哈希地址为H2=(3 + 5)% 11 = 8,此时不再冲突,将69填入8号单元。
- 再哈希法:这种方法是同时构造多个不同的哈希函数:Hi=RH1(key) i=1,2,…,k
当哈希地址Hi=RH1(key)发生冲突时,再计算Hi=RH2(key)……,直到冲突不再产生。这种方法不易产生聚集,但增加了计算时间。
- 链地址法:这种方法的基本思想是将所有哈希地址为i的元素构成一个称为同义词链的单链表,并将单链表的头指针存在哈希表的第i个单元中,因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。
- 方法优点
- 开放定值法:1.记录更容易进行序列化(serialize)操作。 2.如果记录总数可以预知,可以创建完美哈希函数,此时处理数据的效率是非常高的。
- 链地址法: ①对于记录总数频繁可变的情况,处理的比较好(也就是避免了动态调整的开销)。 ②由于记录存储在结点中,而结点是动态分配,不会造成内存的浪费,所以尤其适合那种记录本身尺寸(size)很大的情况,因为此时指针的开销可以忽略不计了。 ③删除记录时,比较方便,直接通过指针操作即可 。
- 方法缺点:
- 开放定值法:1.存储记录的数目不能超过桶数组的长度,如果超过就需要扩容,而扩容会导致某次操作的时间成本飙升,这在实时或者交互式应用中可能会是一个严重的缺陷 2.使用探测序列,有可能其计算的时间成本过高,导致哈希表的处理性能降低 3.由于记录是存放在桶数组中的,而桶数组必然存在空槽,所以当记录本身尺寸(size)很大并且记录总数规模很大时,空槽占用的空间会导致明显的内存浪费 4.删除记录时,比较麻烦。比如需要删除记录a,记录b是在a之后插入桶数组的,但是和记录a有冲突,是通过探测序列再次跳转找到的地址,所以如果直接删除a,a的位置变为空槽,而空槽是查询记录失败的终止条件,这样会导致记录b在a的位置重新插入数据前不可见,所以不能直接删除a,而是设置删除标记。这就需要额外的空间和操作。
- 链地址法: 1.存储的记录是随机分布在内存中的,这样在查询记录时,相比结构紧凑的数据类型(比如数组),哈希表的跳转访问会带来额外的时间开销 2.如果所有的 key-value 对是可以提前预知,并之后不会发生变化时(即不允许插入和删除),可以人为创建一个不会产生冲突的完美哈希函数(perfect hash function),此时封闭散列的性能将远高于开放散列 ③由于使用指针,记录不容易进行序列化(serialize)操作
测试结果
-
画出顺序查找的顺序表和成功平均查找长度。

-
画出折半查找的顺序表和成功平均查找长度。
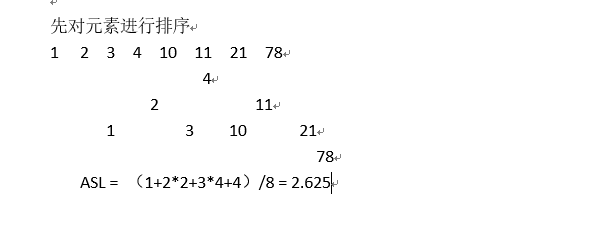
-
用线性探查法实现散列查找。

-
用链地址法实现散列查找。

其他
前几周的内容相对来说比较简单,所以学习的时候有些放松,这次测试也让我明白自己不会的东西还有很多,所以不能懈怠,还要继续努力才是,希望自己能在以后的学习生活中能继续进步!

