雅克比(Jacobi)方法
可以用来求解协方差矩阵的特征值和特征向量。
雅可比方法(Jacobian method)求全积分的一种方法,把拉格朗阶查皮特方法推广到求n个自变量一阶非线性方程的全积分的方法称为雅可比方法。
雅克比迭代法的计算公式简单,每迭代一次只需计算一次矩阵和向量的乘法,且计算过程中原始矩阵A始终不变,比较容易并行计算。
考虑线性方程组Ax=b时,一般当A为低阶稠密矩阵时,用主元消去法解此方程组是有效方法。但是,对于由工程技术中产生的大型稀疏矩阵方程组(A的阶数很高,但零元素较多,例如求某些偏微分方程数值解所产生的线性方程组),利用迭代法求解此方程组就是合适的,在计算机内存和运算两方面,迭代法通常都可利用A中有大量零元素的特点。雅克比迭代法就是众多迭代法中比较早且较简单的一种,其命名也是为纪念普鲁士著名数学家雅可比。
原理
【收敛性】设Ax=b,其中A=D+L+U为非奇异矩阵,且对角阵D也非奇异,则当迭代矩阵J的谱半径ρ(J)<1时,雅克比迭代法收敛。
首先将方程组中的系数矩阵A分解成三部分,即:A = L+D+U,其中D为对角阵,L为下三角矩阵,U为上三角矩阵。
- 之后确定迭代格式,X^(k+1) = B*X^(k) +f ,(这里^表示的是上标,括号内数字即迭代次数),其中B称为迭代矩阵,雅克比迭代法中一般记为J。(k = 0,1,......)
- 再选取初始迭代向量X^(0),开始逐次迭代。


【优缺点】雅克比迭代法的优点明显,计算公式简单,每迭代一次只需计算一次矩阵和向量的乘法,且计算过程中原始矩阵A始终不变,比较容易并行计算。然而这种迭代方式收敛速度较慢,而且占据的存储空间较大,所以工程中一般不直接用雅克比迭代法,而用其改进方法。
实现
通过雅克比(Jacobi)方法求实对称矩阵的特征值和特征向量操作步骤:S′=GTSG,其中G是旋转矩阵,S′和S均为实对称矩阵,S′和S有相同的Frobenius norm,可以用一个最简单的3维实对称矩阵为例,根据公式进行详细推导(参考 维基百科 ):
通过旋转矩阵将对称矩阵转换为近似对角矩阵,进而求出特征值和特征向量,对角矩阵中主对角元素即为S近似的实特征值。Jacobi是通过迭代方法计算实对称矩阵的特征值和特征向量。
计算步骤:
(1)、初始化特征向量V为单位矩阵;
(2)、初始化特征值eigenvalues为矩阵S主对角线元素;
(3)、将二维矩阵S赋值给一维向量A;
(4)、查找矩阵S中,每行除主对角元素外(仅上三角部分)绝对值最大的元素的索引赋给indR;
(5)、查找矩阵S中,第k列,前k个元素中绝对值最大的元素的索引赋给indC;
(6)、查找pivot的索引(k, l),并获取向量A中绝对值最大的元素p;
(7)、如果p的绝对值小于设定的阈值则退出循环;
(8)、计算sinθ(s)和cosθ(c)的值;
(9)、更新(k, l)对应的A和eigenvalues的值;
(10)、旋转A的(k,l);
(11)、旋转特征向量V的(k,l);
(12)、重新计算indR和indC;
(13)、循环执行以上(6)~(12)步,直到达到最大迭代次数,OpenCV中设置迭代次数为n*n*30;
(14)、如果需要对特征向量和特性值进行sort,则执行sort操作。
相关概念
旋转
旋转矩阵性质:设M是任何维的一般旋转矩阵:M∈Rn*n
- (1)、两个向量的点积(内积)在它们都被一个旋转矩阵操作之后保持不变:a·b=Ma·Mb;
- (2)、从而得出旋转矩阵的逆矩阵是它的转置矩阵:MM-1=MMT=I 这里的I是单位矩阵;
- (3)、一个矩阵是旋转矩阵,当且仅当它是正交矩阵并且它的行列式是单位一。正交矩阵的行列式是±1;则它包含了一个反射而不是真旋转矩阵;
- (4)、旋转矩阵是正交矩阵,如果它的列向量形成Rn的一个正交基,就是说在任何两个列向量之间的标量积是零(正交性)而每个列向量的大小是单位一(单位向量)。
在二维空间中,旋转可以用一个单一的角θ定义。作为约定,正角表示逆时针旋转。把笛卡尔坐标的列向量关于原点逆时针旋转θ的矩阵是:
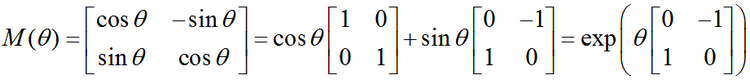
对角矩阵
对角矩阵(diagonal matrix):只在主对角线上含有非零元素,其它位置都是零,对角线上的元素可以为0或其它值。形式上,矩阵D是对角矩阵,当且仅当对于所有的i≠j, Di,j= 0. 单位矩阵就是对角矩阵,对角元素全部是1。
用diag(v)表示一个对角元素由向量v中元素给定的对角方阵。
对角矩阵的乘法计算很高效。计算乘法diag(v)x,我们只需要将x中的每个元素xi放大vi倍。换言之,diag(v)x = v⊙x。
计算对角方阵的逆矩阵也很高效。对角方阵的逆矩阵存在,当且仅当对角元素都是非零值,在这种情况下,diag(v)-1=diag([1/v1, …, 1/vn]T)。
通过将一些矩阵限制为对角矩阵,我们可以得到计算代价较低的(并且简明扼要的)算法。
特征分解
特征分解:线性代数中,特征分解(Eigende composition),又称谱分解(Spectral decomposition)是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。
需要注意只有对可对角化矩阵(如果一个方块矩阵A相似于对角矩阵,也就是说,如果存在一个可逆矩阵P使得P-1AP是对角矩阵,则它就被称为可对角化的)才可以施以特征分解。
特征分解(eigen decomposition)是使用最广的矩阵分解之一,即我们将矩阵分解成一组特征向量和特征值。
方阵A的特征向量(eigen vector)是指与A相乘后相当于对该向量进行缩放的非零向量v:Av=λv。标量λ被称为这个特征向量对应的特征值(eigenvalue)。(类似地,我们也可以定义左特征向量(left eigen vector) vTA=λVT,但是通常我们更关注右特征向量(right eigen vector))。 如果v是A的特征向量,那么任何缩放后的向量sv(s∈R,s≠0)也是A的特征向量。此外,sv和v有相同的特征值。基于这个原因,通常我们只考虑单位特征向量。
假设矩阵A有n个线性无关的特征向量{v(1),…,v(n)},对应着特征值{λ1,…,λn}。我们将特征向量连接成一个矩阵,使得每一列是一个特征向量:V=[v(1),…,v(n)]。类似地,我们也可以将特征值连接成一个向量λ=[λ1,…,λn]T。因此A的特征分解(eigen decomposition)可以记作:A=Vdiag(λ)V-1。
在某些情况下,特征分解存在,但是会涉及到复数,而非实数。每个实对称矩阵都可以分解成实特征向量和实特征值:A=QΛQT。其中Q是A的特征向量组成的正交矩阵,Λ是对角矩阵。特征值Λi,i对应的特征向量是矩阵Q的第i列,记作Q:,i。因为Q是正交矩阵,我们可以将A看作是沿方向v(i)延展λi倍的空间。
虽然任意一个实对称矩阵A都有特征分解,但是特征分解可能并不唯一。如果两个或多个特征向量拥有相同的特征值,那么在由这些特征向量产生的生成子空间中,任意一组正交向量都是该特征值对应的特征向量。
所有特征值都是正数的矩阵被称为正定(positive definite);所有特征值都是非负数的矩阵被称为半正定(positive semidefinite)。同样地,所有特征值都是负数的矩阵被称为负定(negative definite);所有特征值都是非正数的矩阵被称为半负定(negative semidefinite)。半正定矩阵受到关注是因为它们保证Ⅴx,xTAx≥0。此外,正定矩阵还保证xTAx=0 =>x=0。
参考
https://en.wikipedia.org/wiki/Jacobi_eigenvalue_algorithm
https://blog.csdn.net/fengbingchun/article/details/72801310?utm_source=blogxgwz0

 浙公网安备 33010602011771号
浙公网安备 33010602011771号