独立成分分析(Independent component analysis, ICA)
原理概述
中心极限定理表明:对于混合信号,其概率密度比任何一个源信号的概率分布都接近高斯分布;反过来,最大化信号的非高斯性与最大化信号的统计独立性是一致的,这是ICA的基本原理。
ICA是盲源分离(Blind Source Sepatation,BSS)的一种方法,将混合的信号分离成潜在的信息成分。“盲”的意思即这种方法能在不知或知道很少声源信号属性的情况下将其分离开来。
假设两个说话人同时对着两个位于不同位置的麦克风说话,两个麦克风接收到的信号是两个语音的混合信号,即x1(t)和x2(t),其中x1和 x2表示幅度,t为时间坐标。每个麦克风接收到的信号是两个说话人语音的加权和,假设是线性瞬时混合,则
x1(t) = a11s1+ a12s2
x2(t) = a21s1+ a22s2
其中a11, a12,a21和a21是由说话人与麦克风之间距离决定的参数。盲源分离就是仅利用麦克风接收到的信号x1(t)和x2(t)去估计出原始语音信号s1(t)和s2(t),这就是著名的“鸡尾酒会”问题(cocktail party problem)。
解决这一问题的一种方法就是利用信号si(t)的一些统计信息来估测出aij,从而便解方程组得到s1(t)和s2(t)。在s1(t)和s2(t)统计独立的情况下,独立成分分析能很好解决这一问题。
假设混合变量和独立成分都是零均值的,即使不是零均值,也可通过减去一个平均值使之变为零均值。假设有n个独立成分,用向量和矩阵将独立成分分析模型一般化为
x = As
其中x=[x1,x2 …xn]为麦克风接收到的观察信号,A=[ a11,a12,…,a1n; a21,a22,…a2n;…;an1,an2,…,ann]T为混合矩阵,s=[ s1,s2 …sn]为待求解的独立信号。这里没有考虑噪声,A和s均是未知的,仅假设si是相互独立的且xi至多只有一个是高斯分布。利用独立成分分析解出A,对其求逆得W=A-1,则独立信号即可解得
s = Wx
一个独立成分分析方法本质是上一个目标函数加上一个自适应更新算法。
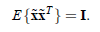
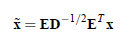
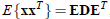
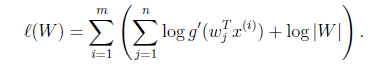
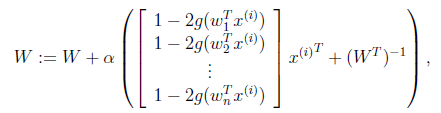
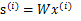
ICA和PCA
PCA指的是主成分分析;其样本的主元正交,样本必须符合高斯分布,源信号之间是非相关的。
主要作用:数据降维。
PCA的过程实际上就是求协方差矩阵的特征值和特征向量,然后做数据转换。
PCA和ICA的用途完全不同。如果只在意数据的能量或方差、假设噪声或不感兴趣的信号都比较微弱,那么用PCA就能把主要信号留下来。在某种意义上,ICA更智能——它不在意信号的能量或方差,只看独立性。所以给定的待分析的混合信号经任意的线性变换都不会影响ICA的输出结果,但会严重影响PCA的结果。
PCA是将原始数据降维并提取出不相关的属性,而ICA是将原始数据降维并提取出相互独立的属性。
ICA要求找到最大独立的方向,各成分是独立的;PCA要求找到最大方差的方向,各成分是正交的。
ICA认为观测信号是若干个统计独立的分量的线性组合,ICA要做的是一个解混过程。而PCA是一个信息提取的过程,将原始数据降维,现已成为ICA将数据标准化的预处理步骤。
两个随机变量独立则它们一定不相关,但2个随机变量不相关则不能保证它们不独立,因为独立是表示没有任何关系,而不相关只能表明是没有线性关系。
一些资料
https://www.cnblogs.com/huanjing/p/8395102.html
https://www.cnblogs.com/xingshansi/p/6884273.html
https://wenku.baidu.com/view/09a95cb569dc5022aaea005d.html
https://www.cnblogs.com/Dinging006/p/8482884.html

