Loss 学习笔记

在机器学习中，我们使用 loss/cost 表示当前模型与理想模型的差距。训练的目的，就是不断缩小 loss/cost。
简单直接的classification error 很难精确描述模型与理想模型之间的距离。需要建立别的更有效的loss函数。
基础可参考：深度学习常用损失函数总览：基本形式、原理、特点 (qq.com)

pytorch中常用的方法如下：

每个损失函数的构造函数都会有自己的参数
criterion = LossCriterion()
loss = criterion(x, y)

模型训练——Loss函数

训练过程中的Loss

炼丹师的自我修养：如何分析训练过程loss异常 (qq.com)

在面对模型不收敛的时候，首先要保证训练的次数够多。在训练过程中，loss并不是一直在下降，准确率一直在提升的，会有一些震荡存在。只要总体趋势是在收敛就行。若训练次数够多（一般上千次，上万次，或者几十个epoch）没收敛，再考虑采取措施解决。

• train loss 不断下降，test loss不断下降，说明网络仍在学习;
• train loss 不断下降，test loss趋于不变，说明网络过拟合;
• train loss 趋于不变，test loss不断下降，说明数据集100%有问题;
• train loss 趋于不变，test loss趋于不变，说明学习遇到瓶颈，需要减小学习率或批量数目;
• train loss 不断上升，test loss不断上升，说明网络结构设计不当，训练超参数设置不当，数据集经过清洗等问题。

Cross-Entropy-Loss

交叉熵损失函数的目的就是使目标端输出的分布与真实分布尽可能一致。

交叉熵，部分参考：

博客 - 神经网络的分类模型 LOSS 函数为什么要用 CROSS ENTROPY
知乎 - 损失函数 - 交叉熵损失函数
PyTorch（七）——损失函数

如果用 MSE 计算 loss，输出的曲线是波动的，有很多局部的极值点。 即，非凸优化问题 (non-convex)。cross entropy 计算 loss，则依旧是一个凸优化问题，用梯度下降求解时，凸优化问题有很好的收敛特性。
cross-entropy 更清晰的描述了模型与理想模型的距离。交叉熵主要是用来判定实际的输出与期望的输出的接近程度。注意：交叉熵不是对称的。
交叉熵的计算公式为：

\[CE = - \sum\limits_{k = 1}^N {{p_k}\log {q_k}} \]

其中p表示真实值，在这个公式中是one-hot形式；log底数为2，q是预测值，在这里假设已经是经过softmax后的结果了。

分类问题，都用 one hot + cross entropy
training 过程中，分类问题用 cross entropy，回归问题用 mean squared error。
training 之后，validation/testing 时，使用 classification error，更直观，而且是我们最关注的指标。

模型预测学习过程中：

1. 神经网络最后一层得到每个类别的得分scores；
2. 该得分经过sigmoid(或softmax)函数获得概率输出；
3. 模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。

使用逻辑函数得到概率，并结合交叉熵当损失函数时，在模型效果差的时候学习速度比较快，在模型效果好的时候学习速度变慢。
sigmoid(softmax) + cross-entropy loss 擅长于学习类间的信息，因为它采用了类间竞争机制，它只关心对于正确标签预测概率的准确性，忽略了其他非正确标签的差异，导致学习到的特征比较散。基于这个问题的优化有很多，比如对softmax进行改进，如L-Softmax、SM-Softmax、AM-Softmax等。（由于交叉熵涉及到计算每个类别的概率，所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。）
使用交叉熵损失函数，不仅可以很好的衡量模型的效果，又可以很容易的的进行求导计算。
另，sigmoid计算公式为：

\[sigmoid(z) = \frac{{{e^z}}}{{1 + {e^z}}} \]

softmax的计算公式为：

\[{softmax}({z_i}) = \frac{{{e^{{z_i}}}}}{{\sum\nolimits_{i = 1}^K {{e^{{z_i}}}} }} \]

交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。

torch.nn.CrossEntropyLoss()

多分类，训练过程中使用。首先，import torch.nn as nn 部分参考：

博客 - pytorch损失函数之nn.CrossEntropyLoss()、nn.NLLLoss()

CrossEntropyLoss带权重的计算公式为（默认weight=None）（不带权重的话，公式中不包含外层括号外的weight[class]）：

\[loss(x,class) = weight[class]\left( { - x[class] + \log (\sum\limits_i {\exp \left( {x[i]} \right)} )} \right) \]

\[loss(x,class) = - \log \frac{{\exp \left( {x\left[ {class} \right]} \right)}}{{\sum\nolimits_i {\exp \left( {x[i]} \right)} }} \]

用于多分类问题，nn.CrossEntropyLoss()是nn.logSoftmax()和nn.NLLLoss()的整合,可以直接使用它来替换网络中的这两个操作。
直接使用pytorch中的loss_func=nn.CrossEntropyLoss()计算得到的结果与softmax-log-NLLLoss计算得到的结果是一致的。

class torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')   

pytorch源码

1. weight (Tensor, optional) – a manual rescaling weight given to each class. If given, has to be a Tensor of size C
2. size_average (bool, optional) – Deprecated (see reduction). By default, the losses are averaged over each loss element in the batch. Note that for some losses, there are multiple elements per sample. If the field size_average is set to False, the losses are instead summed for each minibatch. Ignored when reduce is False. Default: True
3. ignore_index (int, optional) – Specifies a target value that is ignored and does not contribute to the input gradient. When size_average is True, the loss is averaged over non-ignored targets.
4. reduce (bool, optional) – Deprecated (see reduction). By default, the losses are averaged or summed over observations for each minibatch depending on size_average. When reduce is False, returns a loss per batch element instead and ignores size_average. Default: True
5. reduction (string, optional) – Specifies the reduction to apply to the output: 'none' | 'mean' | 'sum'. 'none': no reduction will be applied, 'mean': the sum of the output will be divided by the number of elements in the output, 'sum': the output will be summed. Note: size_average and reduce are in the process of being deprecated, and in the meantime, specifying either of those two args will override reduction. Default: 'mean'

Large-Margin-Cosine-Loss

所有基于softmax loss改进的损失都有相同的想法：最大化类间方差和最小化类内方差。

参考

• CSDN博客-CosFace:Large Margin Cosine Loss
• 知乎文章-CosFace: Large Margin Cosine Loss 论文笔记

简称LMCL，原用在人脸识别任务中，出自Tencent AI Lab在CVPR 2018的论文：CosFace: Large Margin Cosine Loss for Deep Face Recognition

这个损失函数制定通过采用了特征L2归一化以及权重向量的L2归一化，去除了特征的径向差异带来的影响(这个创新点其实就来自之前的Normface)。引入一个余弦Margin可以在角度空间中增大决策Margin，因此可以实现最小化类内差异，最大化类间差异。
该算法以归一化的特征为输入，以最大化类间余弦Margin来学习判别性特征。
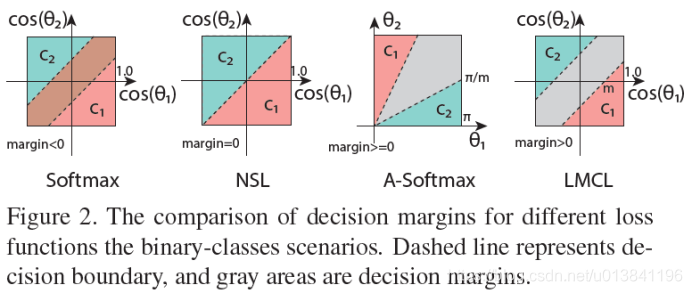
定义一个超参数m>0（两个类别之间有一个明确的边界空间（margin>0），有更好的鲁棒性），定义了一个余弦空间的Margin，决策边界为：

\[\begin{gathered} {C_1}:\cos \left( {{\theta _1}} \right) \geqslant \cos \left( {{\theta _2}} \right) + m \hfill \\ {C_2}:\cos \left( {{\theta _2}} \right) \geqslant \cos \left( {{\theta _1}} \right) + m \hfill \\ \end{gathered}\]

计算公式：

\[{L_{lmc}} = \frac{1}{N}\sum\limits_i { - \log \frac{{{e^{s\left( {\cos \left( {{\theta_{{y_i}}},i} \right) - m} \right)}}}}{{{e^{s\left( {\cos \left( {{\theta_{{y_i}}},i} \right) - m} \right)}} + \sum\nolimits_{j \ne {y_i}} {{e^{s\cos \left( {{\theta_j},i} \right)}}} }}} \]

subject to:

\[\begin{gathered} W = \frac{{{W^*}}}{{\left\| {{W^*}} \right\|}}, \hfill \\ x = \frac{{{x^*}}}{{\left\| {{x^*}} \right\|}}, \hfill \\ \cos \left( {{\theta _j},i} \right) = W_j^T{x_i} \hfill \\ \end{gathered}\]

其中N为训练样本的数目，x_i表示归一化的第i个特征，W_i表示第i类别的权重向量。s为尺度超参数，一般取值较大；m为margin超参数，取小值。

Focal-Loss

参考

• Focal Loss理解 - 三年一梦 - 博客园 (cnblogs.com)
• Focal Loss 理解 - 下路派出所 - 博客园 (cnblogs.com)

本质上讲，Focal Loss 就是一个解决分类问题中类别不平衡、分类难度差异的一个 loss。
这个loss是在交叉熵损失函数基础上进行的修改。普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优。
修改的方式就是“软化”这个 CE loss，“软化”就是把一些本来不可导的函数用一些可导函数来近似，数学角度应该叫“光滑化”。这样处理之后本来不可导的东西就可导了，类似的算例还有梯度下降和EM算法。Focal loss的计算公示如下（演化自二分类交叉熵loss）：

\[{L_{fl}} = \left\{ {\begin{array}{*{20}{c}} { - {{\left( {1 - y'} \right)}^\gamma }\log y',y = 1} \\ { - y{'^\gamma }\log \left( {1 - y'} \right),y = 0} \end{array}} \right.\]

\(y'\)是经过激活函数的输出，所以在0-1之间。上式原有的基础上加了一个因子，其中\(\gamma>0\)使得减少易分类样本的损失。使得更关注于困难的、错分的样本。
\(\gamma\)调节简单样本权重降低的速率，当\(\gamma\)为0时即为交叉熵损失函数，当\(\gamma\)增加时，调整因子的影响也在增加。实验发现\(\gamma=2\)时最优。
Focal Loss 在多分类中的形式如下：

\[{L_{fl}} = - {\left( {1 - y{'_t}} \right)^\gamma }\log y{'_t} \]

\(y{'_t}\)是目标的预测值，一般是经过 softmax 后的结果。

Anchor-Loss

Anchor Loss论文学习_stesha_chen的博客-CSDN博客
一种根据预测难度自动调整cross entropy比例的loss。更多参考上述博客。

Contrastive-Loss

对比损失函数，CTR loss.
对比学习最早被应用在图像领域，通过缩小与正样本间的相似度/距离，扩大与负样本间的相似度/距离，使得正样本与锚点之间的距离远远大于负样本与锚点之间的距离。显然，对于自然语言处理任务来说，对比损失是序列级别(sequence-level)的。

tips

在PyTorch中使用交叉熵损失函数的时候会自动把label转化成onehot，所以不用手动转化，而使用MSE需要手动转化成onehot编码。
几种loss的对比：