归并排序之基本实现及优化
一、基本的归并排序
归并排序分为"分治"和"归并"两个阶段:
分治 : 其中分治采用的是递归的思想将待排序的数组分为越来越小的子数组,直到子数组只有单个元素(将单个元素看做有序数组):过程如图:
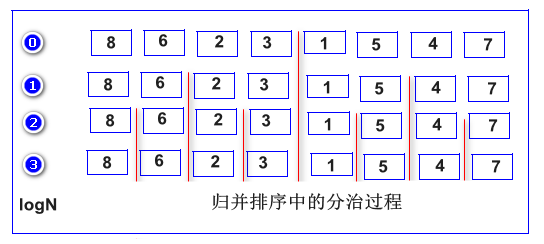
上图所示的分治过程,用代码实现:
public void mergeSorted(int arr[]) { // 元素在 [0...n] 闭区间中 int n = arr.length - 1; __mergeSorted(arr, 0, n); } private void __mergeSorted(int arr[], int L, int R) { // 递归的结束条件 if (L >= R) { // 这里的等号维护 开始的 前闭后闭区间 return; } // 将数组分开的中间元素 int mid = (L + R) / 2; __mergeSorted(arr, L, mid); __mergeSorted(arr, mid + 1, R); // 这里是下一阶段的分治过程 __merge ( arr, L, mid ,R ); } }
归并:归并是将已经排好序的子数组合并在一起,示意图如下,归并的操作过程是:
1. 先创建一个和待合并的两个数组元素之和的数组,同时需要三个指针维护数组的索引位置。
2. 比较前数组第一个元素和后数组的第一个元素,如果前大后小,那么 arr[k] 等于前面数组的元素,否则 arr[k] 等于后面数组的元素。同时维护指针的位置。
3. 前面或者后面的数组元素遍历完后,arr[k] 剩下的元素和其中一部分直接相等。
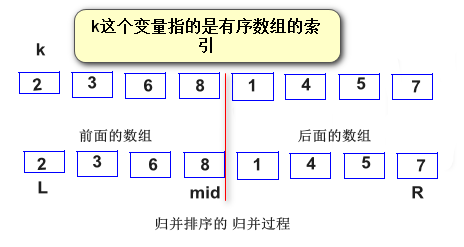
归并的过程代码实现如下 :
private void __merge ( int arr[], int L, int mid, int R ) { int aux[] = new int[R - L + 1]; // 临时变量数组 for ( int i = L; i <= R; i++ ) { aux[i - L] = arr[i]; } // 同时维护三个指针 i j k int i = L; int j = mid + 1; for ( int k = L; k <= R; k++ ) { // 循环比较 if ( i > mid ) { // 前面的数组遍历完了 arr[k] = aux[j - L]; j++; }else if ( j > R ) { // 后面的数组遍历完了 arr[k] = aux [i - L]; i++; }else if (aux[i - L] < aux[j - L]) { // 前面数组的元素较小 arr[k] = aux[i - L]; i++; } else { //后面数组的元素较小 arr[k] =aux[j -L]; j++; } } }
接下来将归并排序的 连个阶段的代码写在一起:

1 public void mergeSorted ( int arr[] ) { 2 3 // 元素在 [0...n] 闭区间中 4 int n = arr.length - 1; 5 __mergeSorted ( arr, 0, n); 6 7 } 8 9 private void __mergeSorted (int arr[], int L, int R ) { 10 11 // 递归的结束条件 12 if ( L >= R ) { // 这里的等号维护 开始的 前闭后闭区间 13 return; 14 } 15 16 将数组分开的中间元素 17 int mid = (L + R ) / 2; 18 19 __mergeSorted (arr, L, mid); 20 __mergeSorted (arr,mid + 1, R); 21 22 // 这里是下一阶段的分治过程 23 __merge ( arr, L, mid ,R ); 24 } 25 26 private void __merge ( int arr[], int L, int mid, int R ) { 27 28 int aux[] = new int[R - L + 1]; // 临时变量数组 29 for ( int i = L; i <= R; i++ ) { 30 aux[i - L] = arr[i]; 31 } 32 33 // 同时维护三个指针 i j k 34 int i = L; 35 int j = mid + 1; 36 for ( int k = L; k <= R; k++ ) { // 循环比较 37 if ( i > mid ) { // 前面的数组遍历完了 38 arr[k] = aux[j - L]; 39 j++; 40 }else if ( j > R ) { // 后面的数组遍历完了 41 arr[k] = aux [i - L]; 42 i++; 43 }else if (aux[i - L] < aux[j - L]) { // 前面数组的元素较小 44 arr[k] = aux[i - L]; 45 i++; 46 } else { //后面数组的元素较小 47 arr[k] =aux[j -L]; 48 j++; 49 } 50 } 51 }
二、 归并排序的优化
1. 取消无谓的归并
归并排序在归并的过程中, 无论前后两个数组如何,都要一一的开辟空间再逐一的比较,我们知道,前后两个数组它本身是有序的。考虑一种极端的情况,如果前面数组的最后一个元素也比后面数组的第一个元素小,那么是不是就没有再归并的必要了呢? 所以,我们第一种优化的方案就是:在归并前加入一个判断。代码如下:
1 public void mergeSorted ( int arr[] ) { 2 3 // 元素在 [0...n] 闭区间中 4 int n = arr.length - 1; 5 __mergeSorted ( arr, 0, n); 6 7 } 8 9 private void __mergeSorted (int arr[], int L, int R ) { 10 11 // 递归的结束条件 12 if ( L >= R ) { // 这里的等号维护 开始的 前闭后闭区间 13 return; 14 } 15 16 将数组分开的中间元素 17 int mid = (L + R ) / 2; 18 19 __mergeSorted (arr, L, mid); 20 __mergeSorted (arr,mid + 1, R); 21 22 // 这里是下一阶段的分治过程 23 // 第一种优化后的代码改变,如果前面数组的最后一个元素小于后面数组的第一个元素,那就不再归并 24 if ( arr[mid] > arr[mid + 1]) { 25 __merge ( arr, L, mid ,R ); 26 } 27 } 28 29 private void __merge ( int arr[], int L, int mid, int R ) { 30 31 int aux[] = new int[R - L + 1]; // 临时变量数组 32 for ( int i = L; i <= R; i++ ) { 33 aux[i - L] = arr[i]; 34 } 35 36 // 同时维护三个指针 i j k 37 int i = L; 38 int j = mid + 1; 39 for ( int k = L; k <= R; k++ ) { // 循环比较 40 if ( i > mid ) { // 前面的数组遍历完了 41 arr[k] = aux[j - L]; 42 j++; 43 }else if ( j > R ) { // 后面的数组遍历完了 44 arr[k] = aux [i - L]; 45 i++; 46 }else if (aux[i - L] < aux[j - L]) { // 前面数组的元素较小 47 arr[k] = aux[i - L]; 48 i++; 49 } else { //后面数组的元素较小 50 arr[k] =aux[j -L]; 51 j++; 52 } 53 } 54 }
2. 减小递归的深度
随着递归的深入,数组越乎近于有序,此时我们用选择排序代替递归,可以优化。代码如下:
1 public void mergeSorted ( int arr[] ) { 2 3 // 元素在 [0...n] 闭区间中 4 int n = arr.length - 1; 5 __mergeSorted ( arr, 0, n); 6 7 } 8 9 private void __mergeSorted (int arr[], int L, int R ) { 10 11 // 递归的结束条件 12 //if ( L >= R ) { // 这里的等号维护 开始的 前闭后闭区间 13 // return; 14 //} 15 16 // 这里是第二处优化的地方,减小递归的深度,随着递归的深入,数组越乎近于有序,此时我们用选择排序代替递归,可以优化 17 if ( R - L <= 15) { 18 insertSorted(arr, L, R); 19 return; 20 } 21 22 23 24 将数组分开的中间元素 25 int mid = (L + R ) / 2; 26 27 __mergeSorted (arr, L, mid); 28 __mergeSorted (arr,mid + 1, R); 29 30 // 这里是下一阶段的分治过程 31 // 第一种优化后的代码改变,如果前面数组的最后一个元素小于后面数组的第一个元素,那就不再归并 32 if ( arr[mid] > arr[mid + 1]) { 33 __merge ( arr, L, mid ,R ); 34 } 35 } 36 37 private void __merge ( int arr[], int L, int mid, int R ) { 38 39 int aux[] = new int[R - L + 1]; // 临时变量数组 40 for ( int i = L; i <= R; i++ ) { 41 aux[i - L] = arr[i]; 42 } 43 44 // 同时维护三个指针 i j k 45 int i = L; 46 int j = mid + 1; 47 for ( int k = L; k <= R; k++ ) { // 循环比较 48 if ( i > mid ) { // 前面的数组遍历完了 49 arr[k] = aux[j - L]; 50 j++; 51 }else if ( j > R ) { // 后面的数组遍历完了 52 arr[k] = aux [i - L]; 53 i++; 54 }else if (aux[i - L] < aux[j - L]) { // 前面数组的元素较小 55 arr[k] = aux[i - L]; 56 i++; 57 } else { //后面数组的元素较小 58 arr[k] =aux[j -L]; 59 j++; 60 } 61 } 62 63 // 减小递归的深度转而使用选择排序 64 private void insertSorted(int arr[], int L, int R) { 65 66 for (int i = L + 1; i <= R; i++) { 67 int i = arr[i]; 68 int j; 69 for (j = i; j > L && arr[j - 1] > e; j--) { 70 arr[j] = arr[j - 1]; 71 } 72 } 73 return; 74 } 75 }
三、 自底向上的归并排序

1 public void mergeSortedBU(int arr[]) { 2 3 int n = arr.length; 4 for ( int size = 0; size <= n; size +=size){ 5 for (int i = 0;i + size < n; i += size +size) 6 __merge(arr, i, i + size -1, Math.min(i +size +size - 1, n - 1)); 7 } 8 } 9 10 private void __merge ( int arr[], int L, int mid, int R ) { 11 12 int aux[] = new int[R - L + 1]; // 临时变量数组 13 for ( int i = L; i <= R; i++ ) { 14 aux[i - L] = arr[i]; 15 } 16 17 // 同时维护三个指针 i j k 18 int i = L; 19 int j = mid + 1; 20 for ( int k = L; k <= R; k++ ) { // 循环比较 21 if ( i > mid ) { // 前面的数组遍历完了 22 arr[k] = aux[j - L]; 23 j++; 24 }else if ( j > R ) { // 后面的数组遍历完了 25 arr[k] = aux [i - L]; 26 i++; 27 }else if (aux[i - L] < aux[j - L]) { // 前面数组的元素较小 28 arr[k] = aux[i - L]; 29 i++; 30 } else { //后面数组的元素较小 31 arr[k] =aux[j -L]; 32 j++; 33 } 34 } 35 }





