LeetCode 初级算法

删除排序数组中的重复项

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int size=nums.size();//获取数组的长度
        int left=0;//定义左指针
        int right=1;//定义右指针
        for(int i=right;i<size;i++){
            if(nums[left]==nums[i]){
                //如果左指针和右指针指向的值相等，则左指针不动，右指针向前移动
                continue;
            }
            if(nums[left]!=nums[i]){
                //如果左指针和右指针指向的值不相等，则左指针向前移动，然后将右指针的值赋给左指针，右指针向前移动
                left++;
                nums[left]=nums[i];
                continue;
            }
        }
        //左指针所处的下标即数组的长度-1
        return left+1;
    }
};

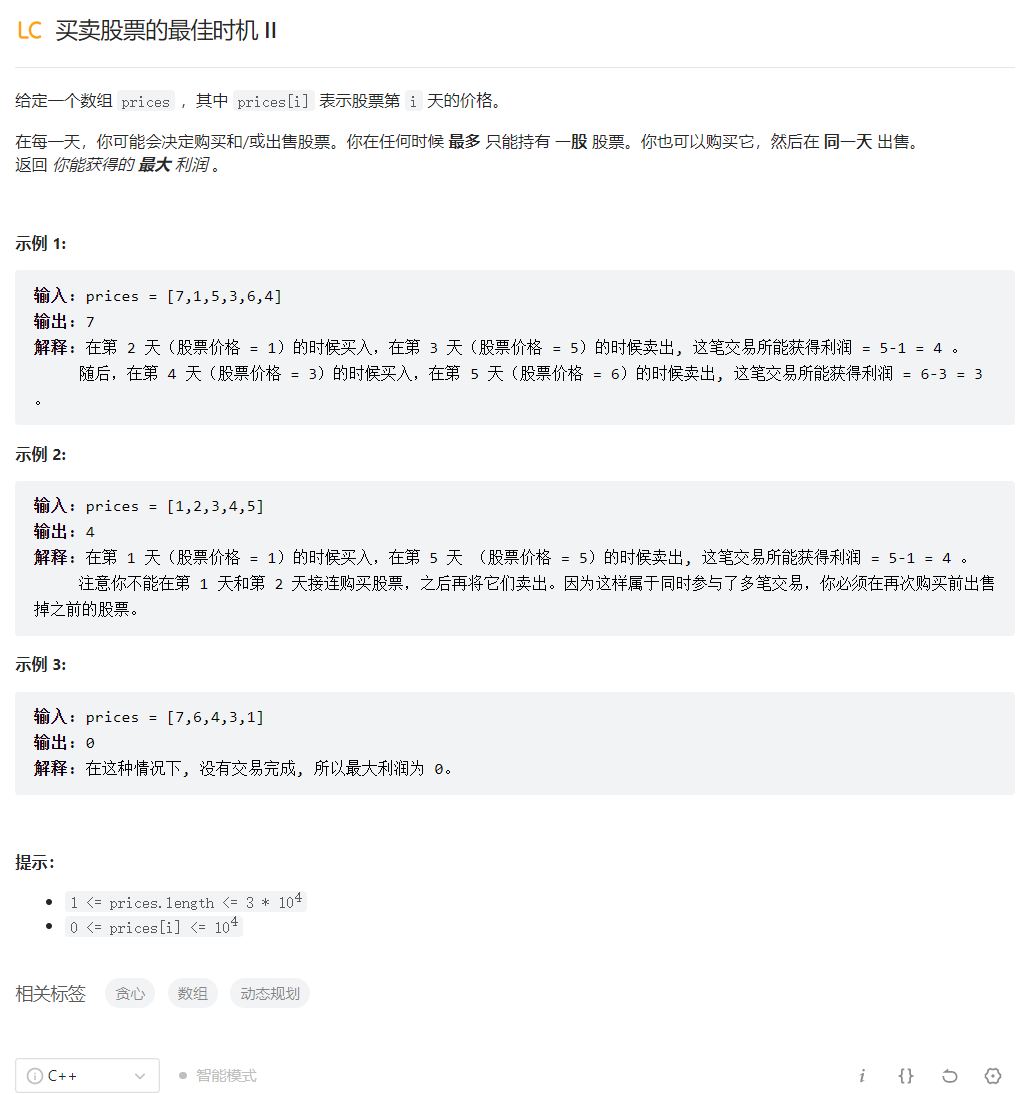
买卖股票的最佳时机 ΙΙ

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //本题相当于求所有上升区间的总和，最简单的方法是贪心法
        int max=0;//收益最大值
        for(int i=1;i<prices.size();i++){
            int price=prices[i]-prices[i-1];//当天价格和前一天价格的差值
            if(price>0){
                //如果差值大于0，则卖出
                max+=price;
            }
        }
        return max;
    }
};

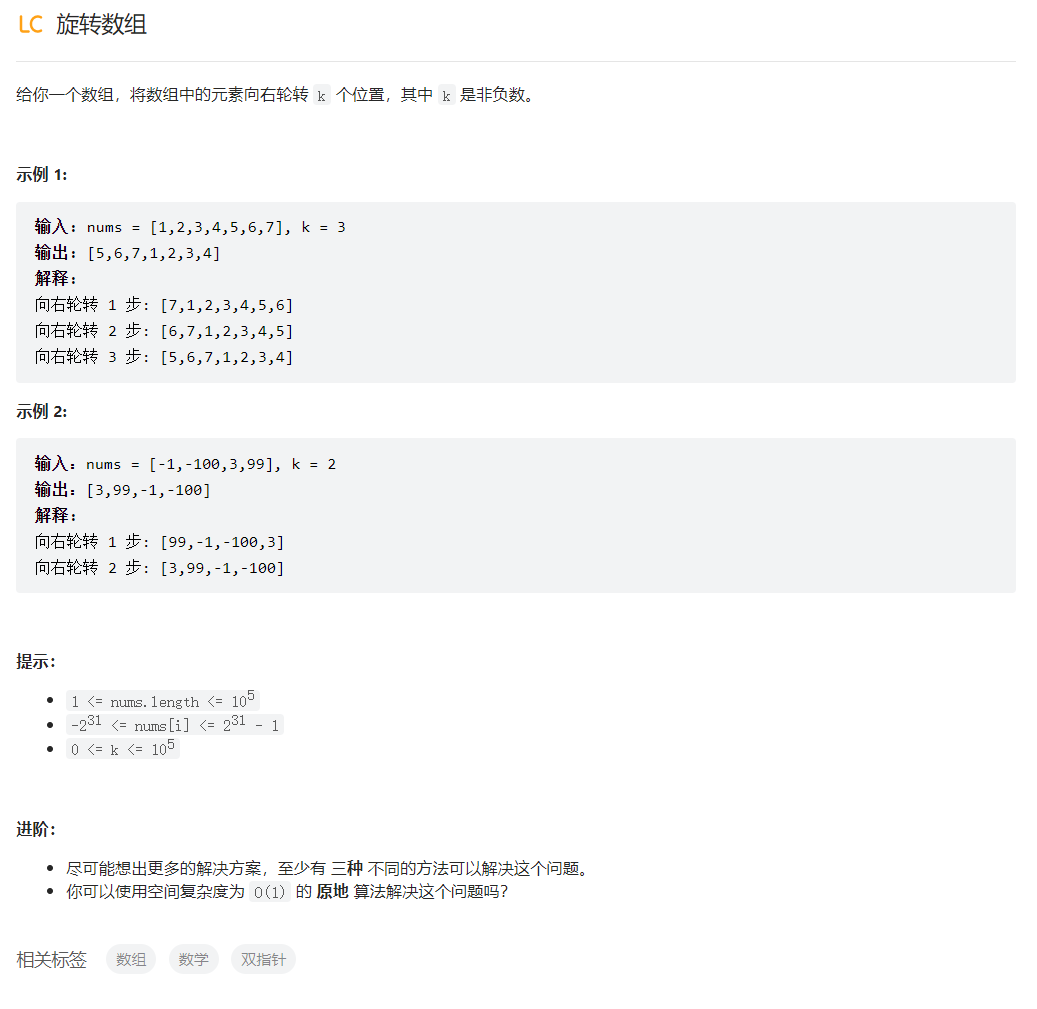
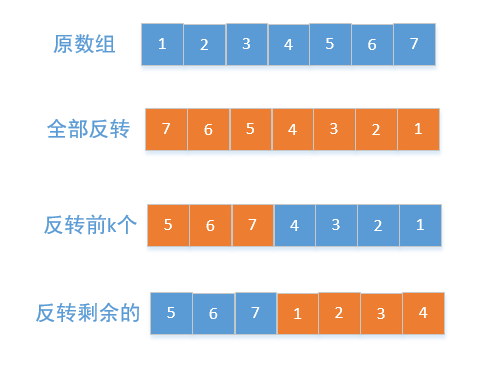
旋转数组

class Solution {
public:
    void reverse(vector<int>& nums,int start,int end){
        while(start<end){
            int temp=nums[start];
            nums[start++]=nums[end];
            nums[end--]=temp;
        }
    }
    void rotate(vector<int>& nums, int k) {
        int size=nums.size();
        k%=size;
        reverse(nums,0,size-1);
        reverse(nums,0,k-1);
        reverse(nums,k,size-1);
    }
};

解题思路

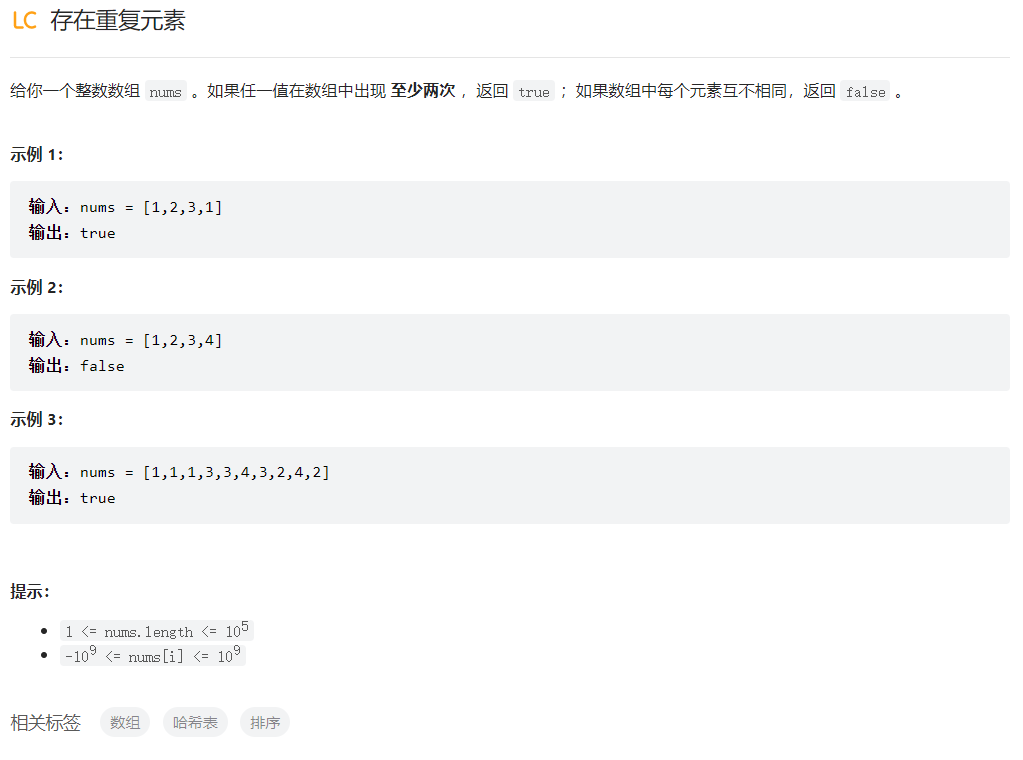
存在重复元素

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        //先排序再比较
        sort(nums.begin(),nums.end());
        for(int i=1;i<nums.size();i++){
            if(nums[i]==nums[i-1]){
                return true;
            }
        }
        return false;
    }
};

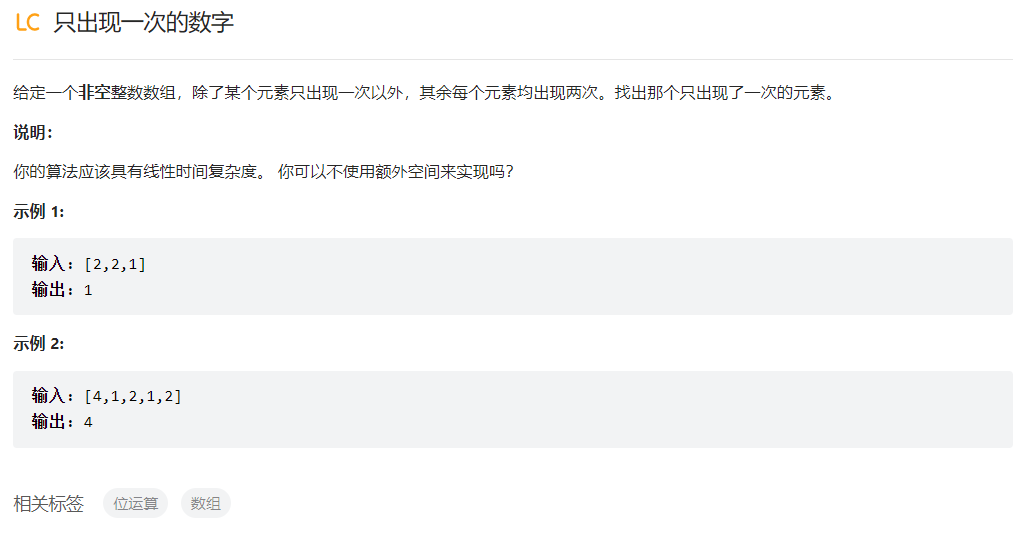
只出现一次的数字

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int result=0;
        for(int i=0;i<nums.size();i++){
            result^=nums[i];
        }
        return result;
    }
};

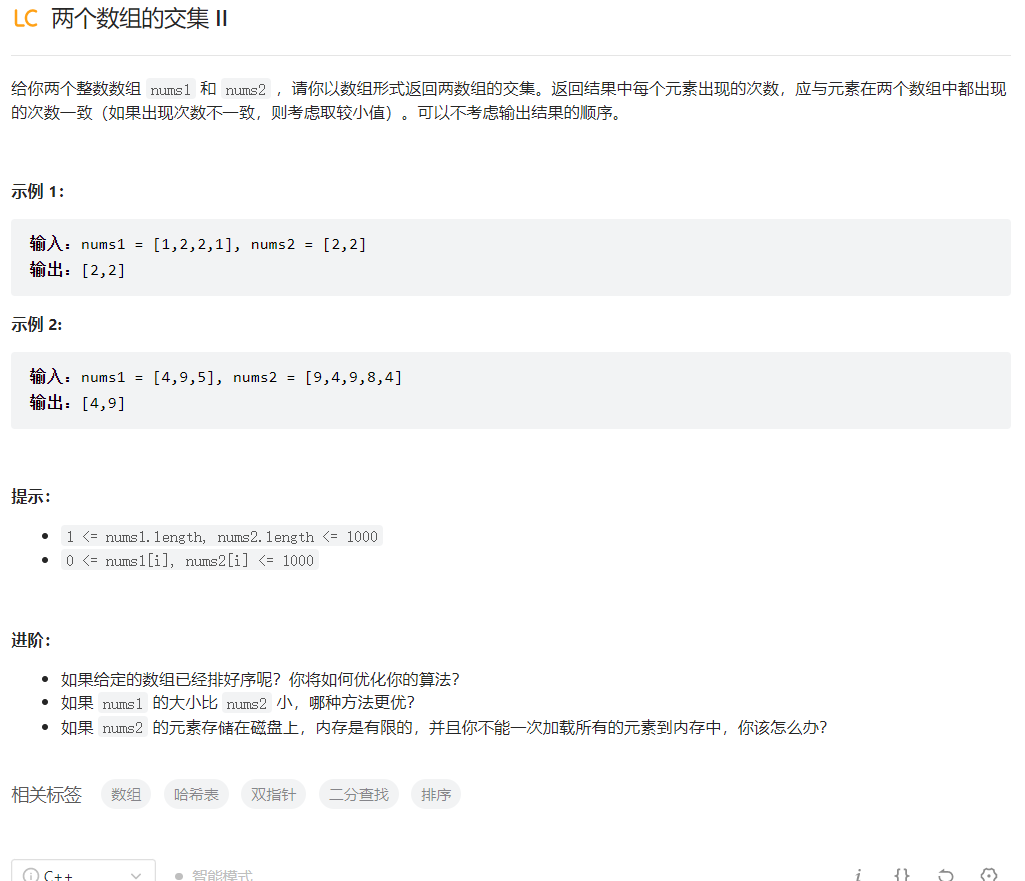
两个数组的交集 ΙΙ

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        //先对nums1和nums2进行排序
        sort(nums1.begin(),nums1.end());
        sort(nums2.begin(),nums2.end());
        vector<int> result;
        int p1=0,p2=0;//定义双指针，初始化为指向数组的第一个元素
        while(p1<nums1.size() && p2<nums2.size()){
            if(nums1[p1]<nums2[p2]){
                //如果p1指向的值小于p2指向的值，则指针p1向前移动
                p1++;
            } else if(nums1[p1]>nums2[p2]) {
                //如果p2指向的值小于p1指向的值，则指针p2向前移动
                p2++;
            } else {
                //如果p1指向的值和p2指向的值相等，则将该值添加到返回数组中，p1和p2同时向前移动
                result.push_back(nums1[p1]);
                p1++;
                p2++;
            }
        }
        return result;
    }
};

加一

class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
        int size=digits.size();
        for(int i=size-1;i>=0;i--){
            //如果i执行的的值为9则将该值置为0，否则将该值+1直接返回结果
            if(digits[i]!=9){
                digits[i]+=1;
                return digits;
            } else {
                digits[i]=0;
            }
        }
        //如果最后一位不是9则执行不到这里
        vector<int> result;
        //将第1位置为1
        result.push_back(1);
        //将其余size位置为0
        for(int i=0;i<size;i++){
            result.push_back(0);
        }
        return result;
    }
};

移动零

class Solution {
public:
    //交换两个数的值
    void swap(int &num1,int &num2){
        int temp=num1;
        num1=num2;
        num2=temp;
    }
    void moveZeroes(vector<int>& nums) {
        //如果数组长度为1则直接结束
        if(nums.size()==1){
            return;
        }
        int p1=0,p2=0;//定义双指针并初始化为0
        while(p2<nums.size()){
            if(nums[p2]!=0){
                //当p2指向的值不为0，并且p1不等于p2时，则交换两个数的值
                if(p1!=p2){
                    swap(nums[p1],nums[p2]);
                }
                //p1向前移动
                p1++;
            }
            //p2向前移动
            p2++;
        }
    }
};

两数之和

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> temp;//定义一个map
        for(int i=0;i<nums.size();i++){
            //如果map中存在target-nums[i]的键值对，则返回结果；否则将{nums[i],i}添加到map中
            unordered_map<int,int>::iterator iter=temp.find(target-nums[i]);
            if(iter!=temp.end()){
                return {iter->second,i};
            }
            pair<int,int> pair(nums[i],i);
            temp.insert(pair);
        }
        return {0,0};
    }
};

有效的数独

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        int row[9]={0},col[9]={0},cell[9]={0};//分别代表行、列、单元格
        int shift;//用于记录位运算后的结果
        for(int i=0;i<board.size();i++){
            for(int j=0;j<board[i].size();j++){
                if(board[i][j]=='.'){
                    //如果当前字符为 . 则直接跳过
                    continue;
                }
                shift=1<<(board[i][j]-'0');
                //k表示当前位于第几个单元格内
                int k=(i/3)*3+j/3;
                //当row[i]&shift>0或者col[j]&shift>0或者cell[k]&shift>0时，表示该值在行内或者列内或者单元格内冲突，直接返回false
                if((row[i]&shift)>0 || (col[j]&shift)>0 || (cell[k]&shift)>0){
                    return false;
                }
                //将row[i]、col[j]、cell[k]与shift相与
                row[i]|=shift;
                col[j]|=shift;
                cell[k]|=shift;
            }
        }
        return true;
    }
};

旋转图像

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int size=matrix.size();
        //上下交换
        for(int i=0;i<size/2;i++){
            for(int j=0;j<matrix[i].size();j++){
                swap(matrix[i][j],matrix[size-i-1][j]);
            }
        }
        //对角线交换
        for(int i=0;i<size;i++){
            for(int j=i+1;j<size;j++){
                swap(matrix[i][j],matrix[j][i]);
            }
        }
    }
};

反转字符串

class Solution {
public:
    void reverseString(vector<char>& s) {
        int left=0,right=s.size()-1;//定义双指针
        while(left<right){
            //交换首尾指针指向的值
            swap(s[left],s[right]);
            left++;//左指针向前移动
            right--;//右指针向后移动
        }
    }
};

整数反转

class Solution {
public:
    int reverse(int x) {
        long res=0;//定义返回的结果
        while(x!=0){
            int one=x%10;//取当前数的个位数字
            res=res*10+one;//将结果*10+个位
            x/=10;//当前数除以10
        }
        return (int)res==res?(int)res:0;//如果超出范围则强转后与返回结果不等，返回0；否则返回原结果
    }
};

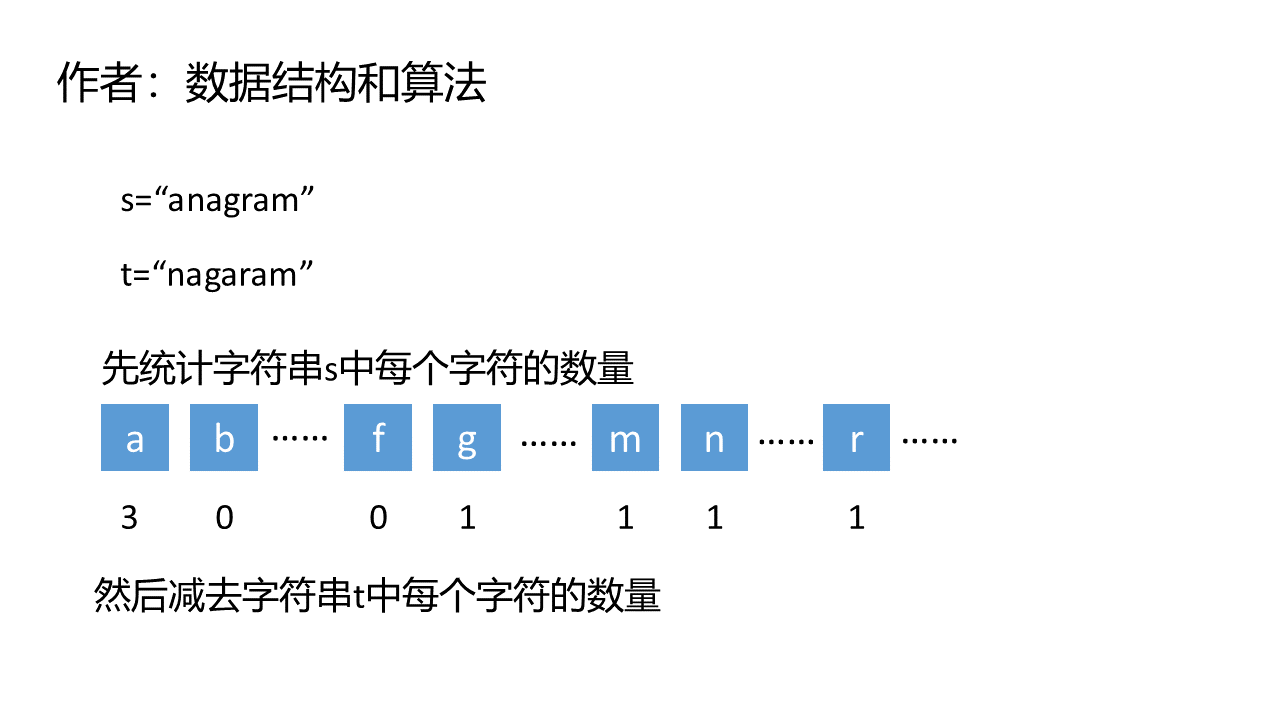
字符串中的第一个唯一字符

class Solution {
public:
    int firstUniqChar(string s) {
        int count[26]={0};
        for(auto c:s){
            count[c-'a']++;
        }
        for(int i=0;i<s.size();i++){
            if(count[s[i]-'a']==1){
                return i;
            }
        }
        return -1;
    }
};

有效的字母异位词

class Solution {
public:
    bool isAnagram(string s, string t) {
        if(s.length()!=t.length()){
            return false;
        }
        int letterCount[26]={0};
        for(auto c:s){
            letterCount[c-'a']++;
        }
        for(auto c:t){
            letterCount[c-'a']--;
        }
        for(auto count:letterCount){
            if(count!=0){
                return false;
            }
        }
        return true;
    }
};

验证回文串

class Solution {
public:
    //判断该字符是否是字母或者是数字
    bool isLetterOrDigit(char c){
        if((c>=48&&c<=57)||(c>=65&&c<=90)||(c>=97&&c<=122)){
            return true;
        }
        return false;
    }
    //将字符转换为小写并返回
    char toLower(char c){
        if(c>=65 && c<=90){
            return c+32;
        }
        return c;
    }
    bool isPalindrome(string s) {
        int left=0,right=s.length()-1;//定义双指针，分别指向第一个字符和最后一个字符
        while(left<right){
            if(!isLetterOrDigit(s[left])){
                //如果左指针指向的字符不是字母或数字则左指针向右移动一位
                left++;
                continue;
            }
            if(!isLetterOrDigit(s[right])){
                //如果有指针指向的字符不是字母或数字则右指针向左移动一位
                right--;
                continue;
            }
            //如果左指针和有指针指向的字符不相等则直接返回false
            if(toLower(s[left]) != toLower(s[right])){
                return false;
            }
            //如果左指针和有指针指向的字符相等则左指针向右移动一位，右指针向左移动一位
            left++;
            right--;
        }
        return true;
    }
};

字符串转换整数

class Solution {
public:
    int myAtoi(string s) {
        const int MAX=2147483647;//定义最大值。即2^31-1
        const int MIN=-2147483648;//定义最小值。即-2^31
        bool flag = true;//是否已识别到有效字符。即是否已经识别到数字或正负号。true表示没有识别到，false表示识别到
        int op=1;//数字的符号，判断结果是正数还是负数
        long result=0;//返回的结果
        for(auto c:s){
            if(flag && c==' ')
                continue;
            if(c>='0' && c<='9'){
                flag=false;
            }
            if(flag && c=='-'){
                op=-1;
                flag=false;
                continue;
            }
            if(flag && c=='+'){
                flag=false;
                continue;
            }
            if(c<'0' || c>'9')
                break;
            result=result*10+(c-'0');
            if(result>MAX){
                return op==1?MAX:MIN;
            }
        }
        return (int)result*op;
    }
};

实现 strStr()

class Solution {
public:
    /**
     * 本题是一道经典的KMP算法题，能力有限，示例代码使用的是较容易理解的滑动窗口解决的
     */
    int strStr(string haystack, string needle) {
        if(needle.length()==0){
            return 0;
        }
        int l1=haystack.length(),l2=needle.length();
        bool match;
        for(int i=0;i<l1-l2+1;i++){
            match=true;
            for(int j=0;j<l2;j++){
                if(haystack[j+i]!=needle[j]){
                    match=false;
                    break;
                }
            }
            if(match){
                return i;
            }
        }
        return -1;
    }
};

外观数列

class Solution {
public:
    string countAndSay(int n) {
        if(n==1){
            return "1";
        }
        string temp=countAndSay(n-1);
        string result="";
        int count=0;
        char c=temp[0];
        for(int i=0;i<temp.length();i++){
            if(temp[i]==c){
                count++;
            }
            else{
                result+=to_string(count)+c;
                count=1;
                c=temp[i];
            }
        }
        result+=to_string(count)+c;
        return result;
    }
};

解题思路

1. 先确立递归出口 n = 1时 为1
2. 对上一个结果进行遍历获取值
3. 设定计数器，计算同一个数字出现的次数
4. 如果数字相同，计数器加一
5. 若当前不满足，则将上次的值记录下，并重置计数器，重置需要判断是否重复的字符
6. 将最后的结果也追加到字符串上

最长公共前缀

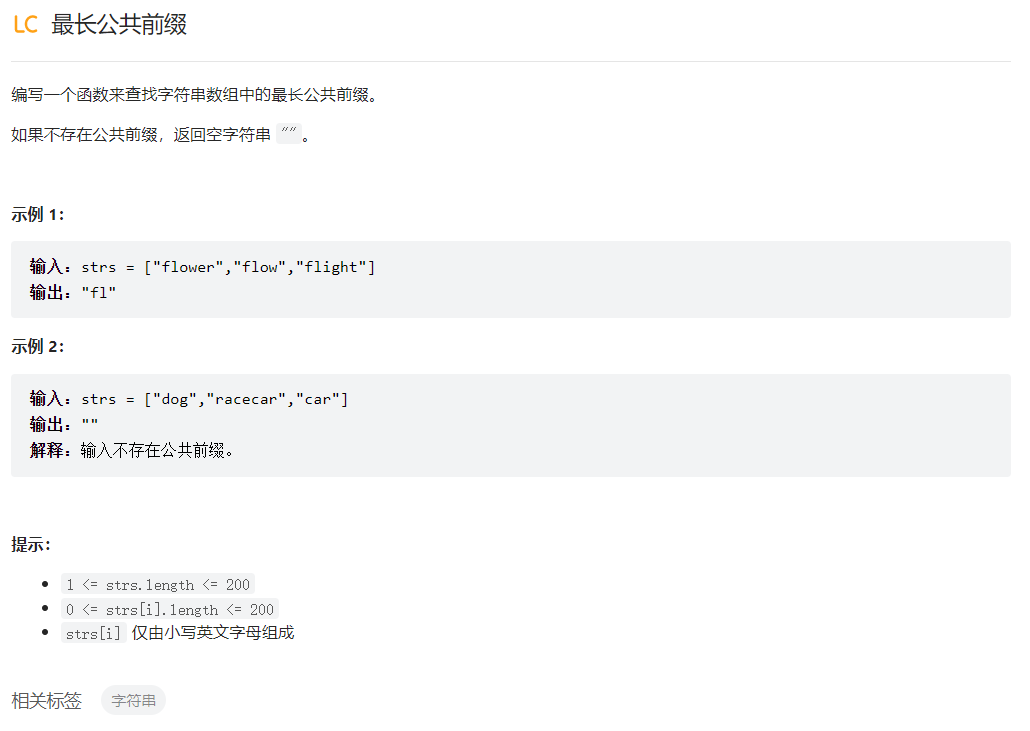
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        int minLength=200;//strs中最短字符串的长度
        for(auto s:strs){
            minLength=minLength<s.length()?minLength:s.length();
        }
        string prefix="";
        //最长公共前缀最长为minLength，所以只需要遍历每个字符串前minLength个字符是否相等
        for(int i=0;i<minLength;i++){
            for(int j=0;j<strs.size()-1;j++){
                if(strs[j][i]!=strs[j+1][i])
                    return prefix;
            }
            prefix+=strs[0][i];
        }
        return prefix;
    }
};

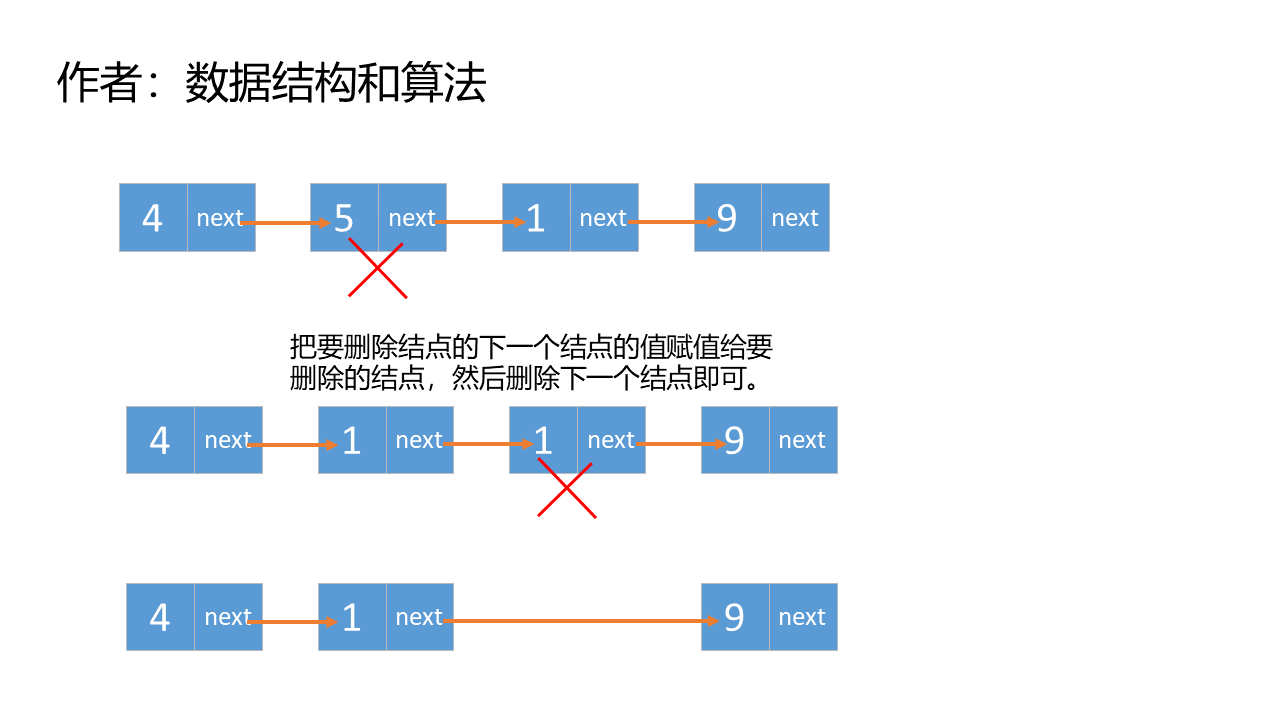
删除链表中的节点

/**
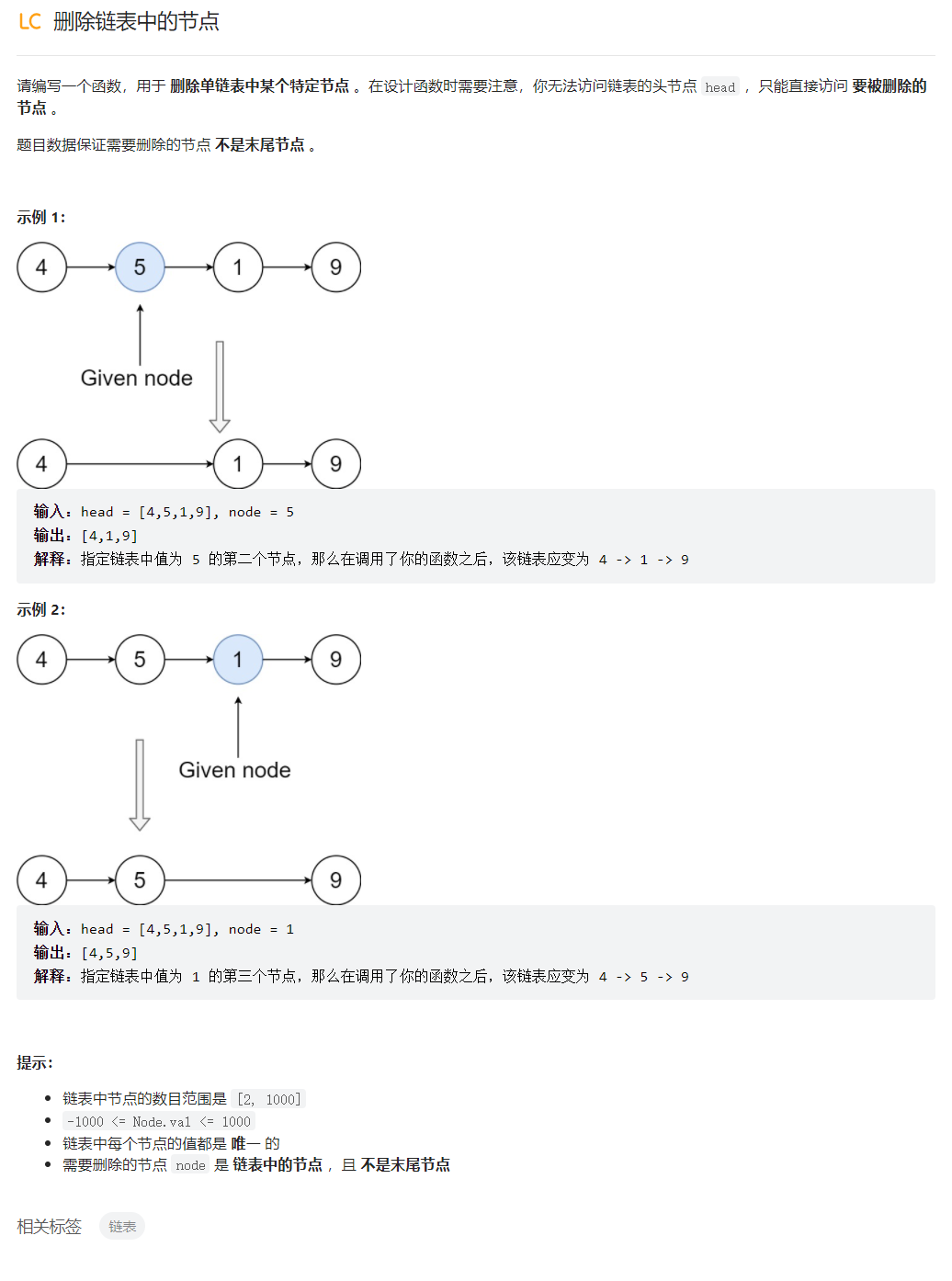
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
        node->val=node->next->val;
        node->next=node->next->next;
    }
};

解题思路

删除链表的倒数第N个节点

/**
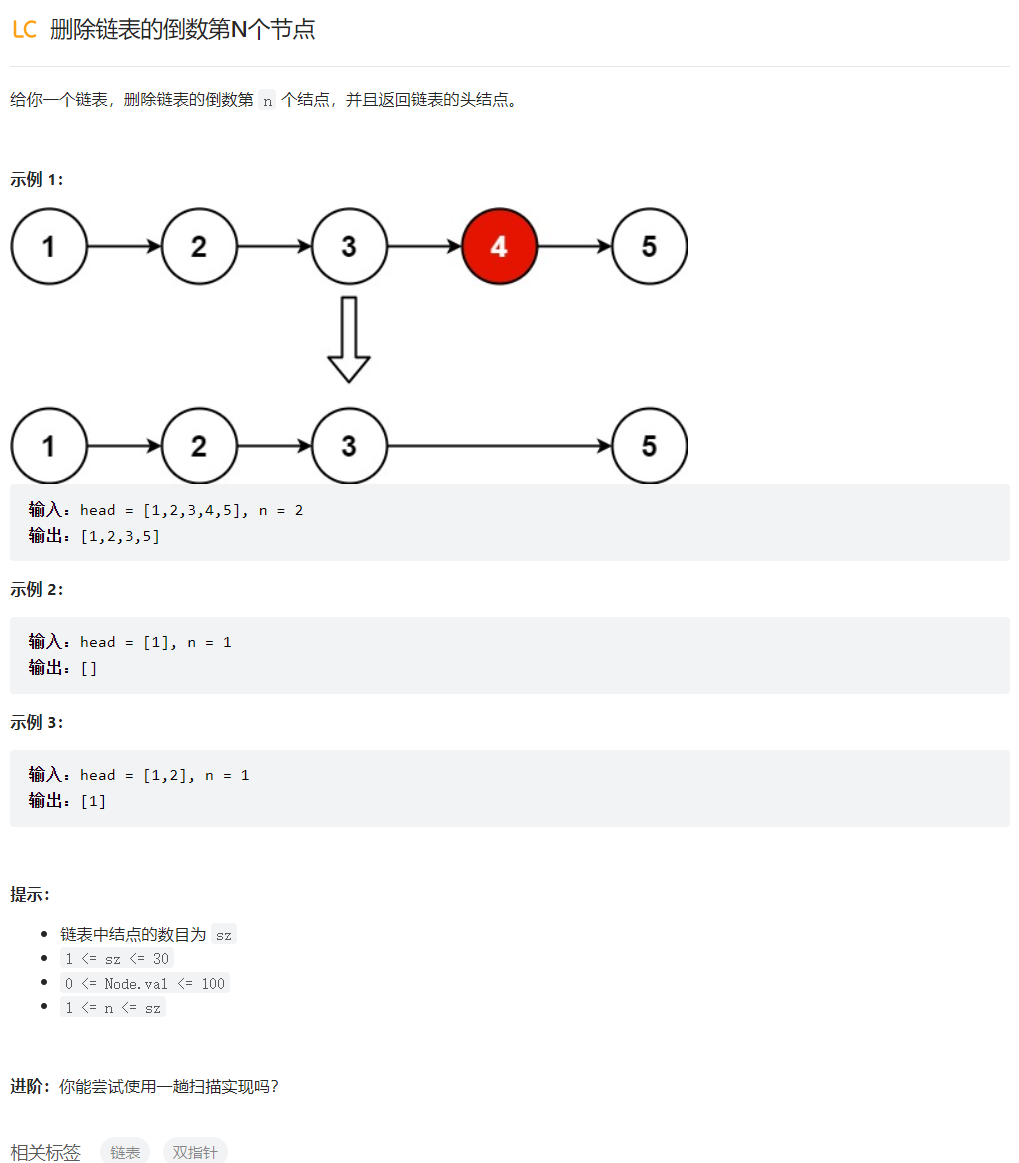
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode *rHead=new ListNode(0,head);//定义一个假的头结点指向头结点
        ListNode *fast=rHead,*slow=rHead;//定义快慢指针
        while(n>0){
            //将块指针向右移动n
            fast=fast->next;
            n--;
        }
        if(n==1){
            //如果n=1，则表示删除的是最后一个，直接将慢指针的next置为nullptr即可，返回假的头结点的next
            slow->next= nullptr;
            return rHead->next;
        }
        while(fast->next!= nullptr){
            //将快慢指针同时向右移动，直至快指针移到最后一个节点
            slow=slow->next;
            fast=fast->next;
        }
        //将slow的next指针指向slow的next->next节点
        slow->next=slow->next->next;
        //返回假的头结点的next即可
        return rHead->next;
    }
};

反转链表

/**
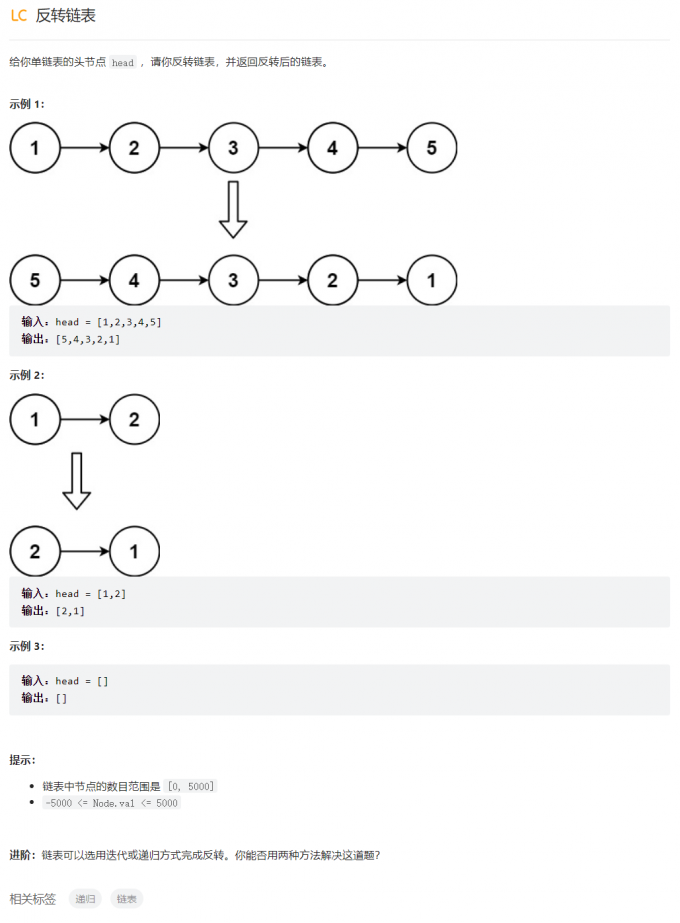
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    /**
     *	使用递归解决
     */
    ListNode* reverseList(ListNode* head) {
        //如果是空链表或者节点的next为nullptr则直接返回head
        if(head==NULL || head->next== nullptr){
            return head;
        }
        //递归调用
        ListNode *reverse=reverseList(head->next);
        head->next->next=head;
        head->next= nullptr;
        return reverse;
    }
};

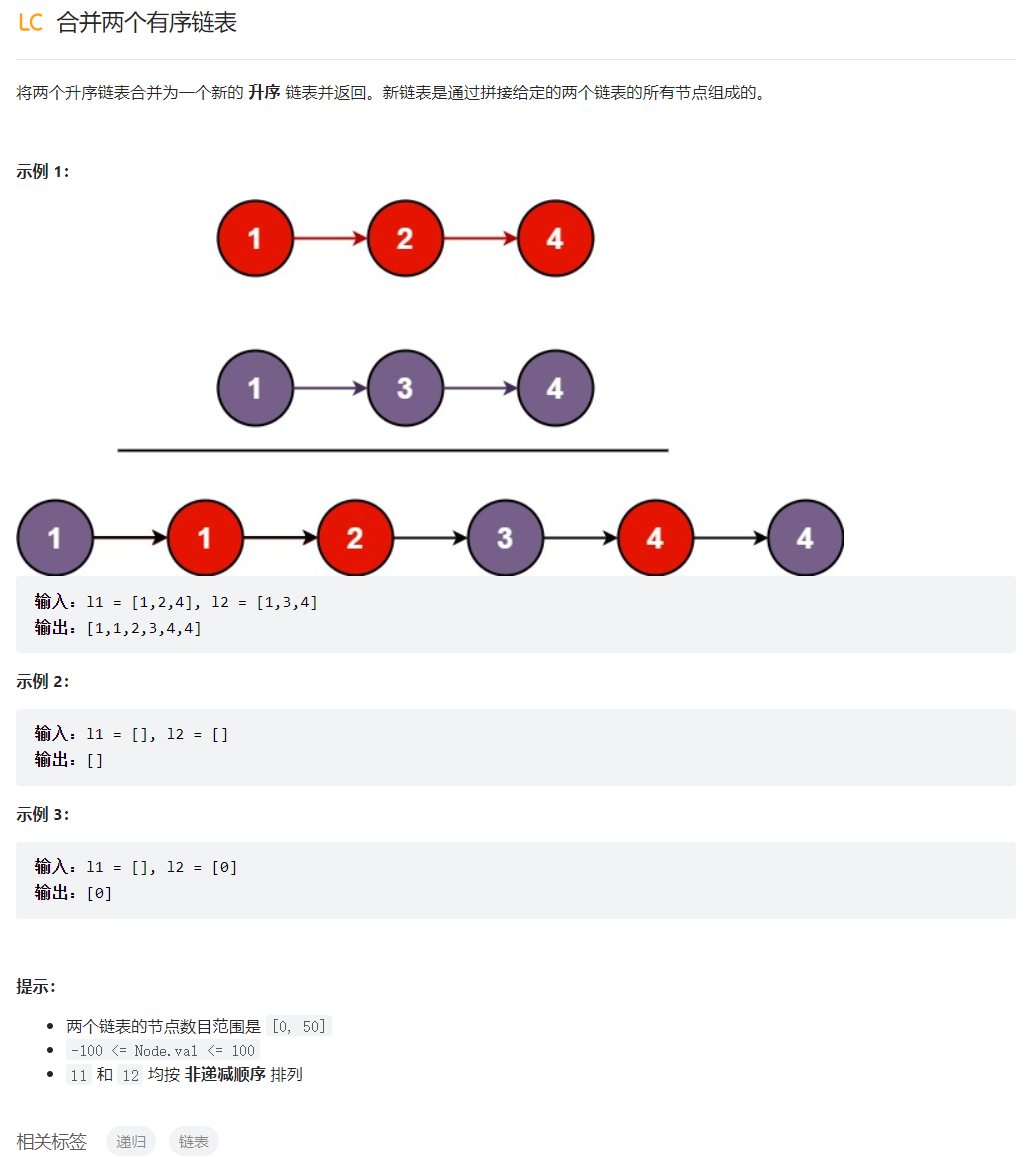
合并两个有序链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    /**
     *	本题使用递归解决
     */
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        //如果list1是空链表则返回list2；如果list2是空链表则返回list1
        if(list1==NULL || list2==NULL){
            return list1==NULL?list2:list1;
        }
        ListNode *head=(list1->val <= list2->val)?list1:list2;
        head->next=mergeTwoLists(head->next,head==list1?list2:list1);
        return head;
    }
};

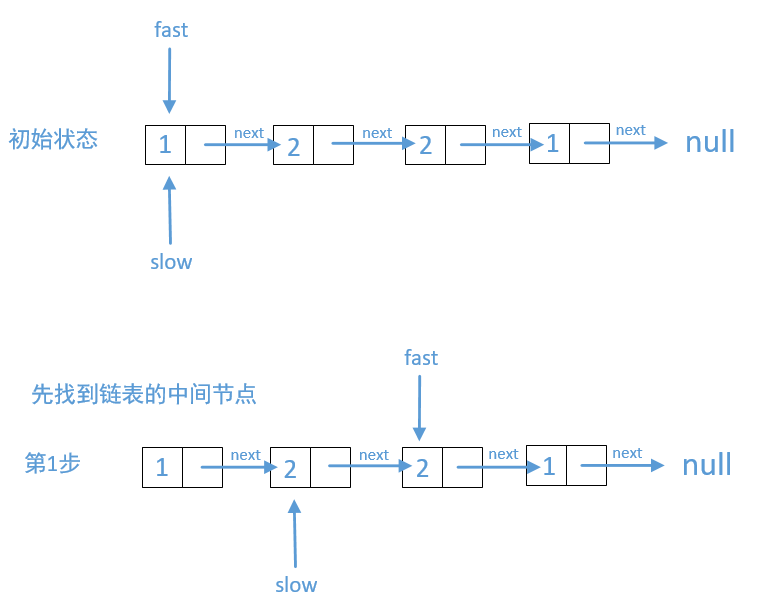
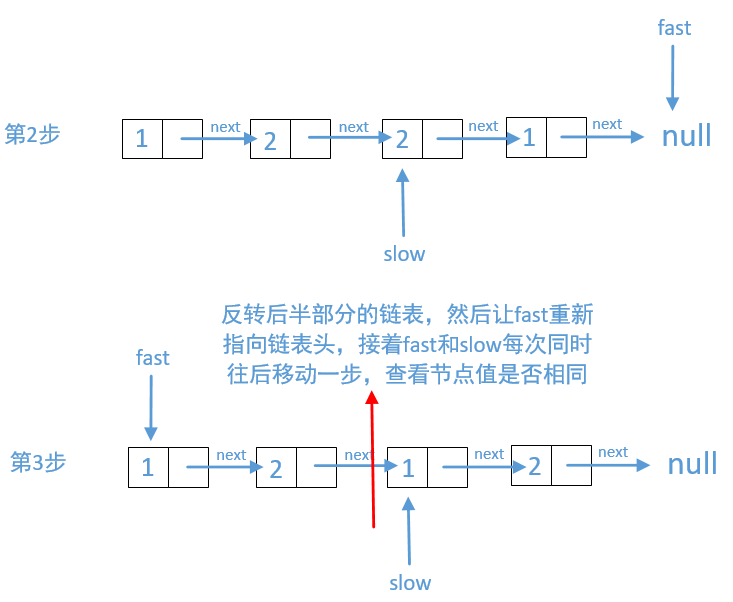
回文链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    //与上面的反转链表算法一样
    ListNode * reverseList(ListNode *head){
        if(head == NULL || head->next == nullptr){
            return head;
        }
        ListNode *reverse=reverseList(head->next);
        head->next->next=head;
        head->next= nullptr;
        return reverse;
    }
    bool isPalindrome(ListNode* head) {
        ListNode *fast=head,*slow=head;
        if(head->next == nullptr){
            return head;
        }
        while(fast->next!=nullptr && fast->next->next != nullptr){
            fast=fast->next->next;
            slow=slow->next;
        }
        slow=reverseList(slow->next);
        fast=head;
        while(slow!= nullptr){
            if(slow->val!=fast->val)
                return false;
            slow=slow->next;
            fast=fast->next;
        }
        return true;
    }
};

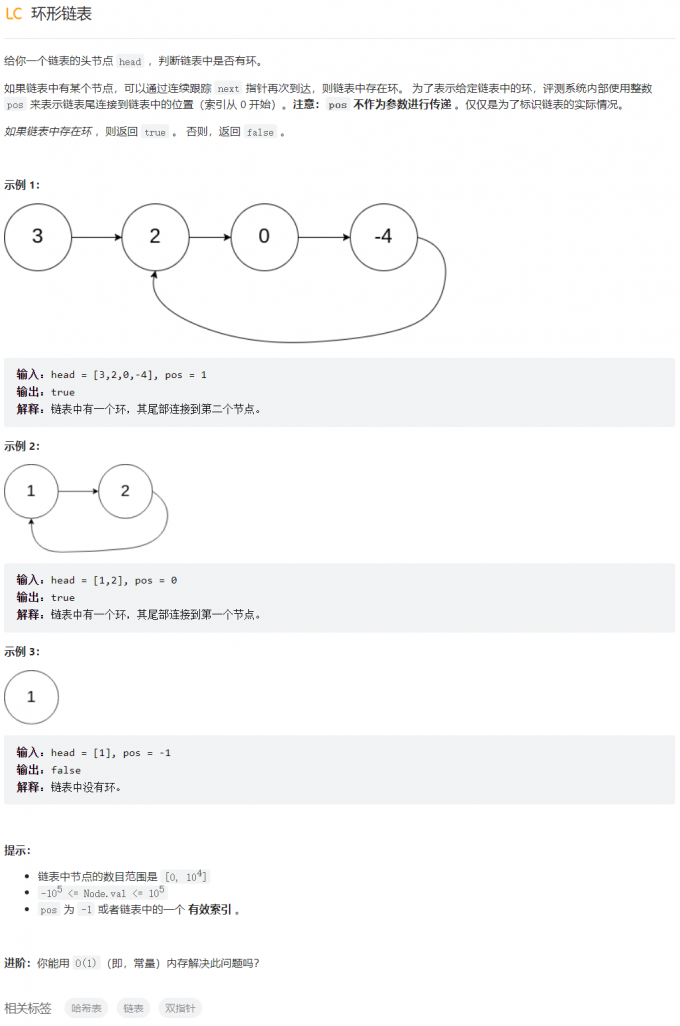
环形链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head==NULL || head->next== nullptr){
            return false;
        }
        ListNode *fast=head,*slow=head;
        while(fast->next!= nullptr && fast->next->next!= nullptr){
            fast=fast->next->next;
            slow=slow->next;
            if(fast==slow){
                return true;
            }
        }
        return false;
    }
};

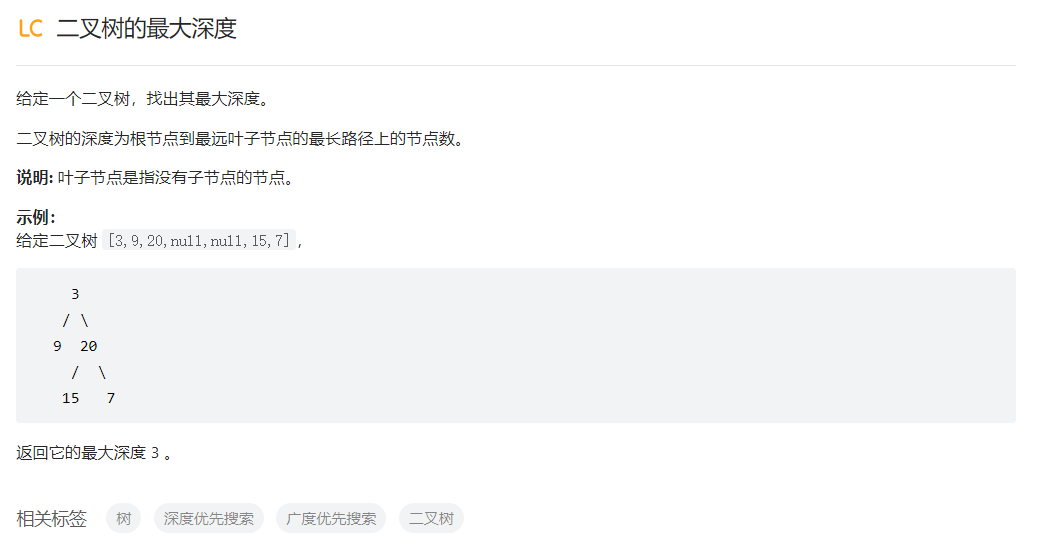
二叉树的最大深度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==NULL){
            return 0;
        }
        return max(maxDepth(root->left),maxDepth(root->right))+1;
    }
};

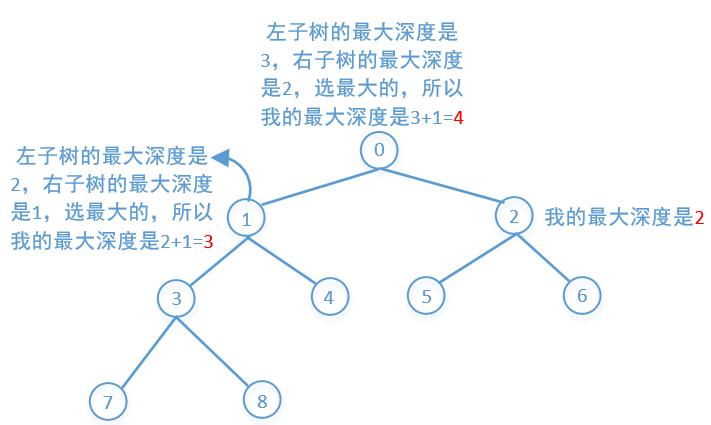
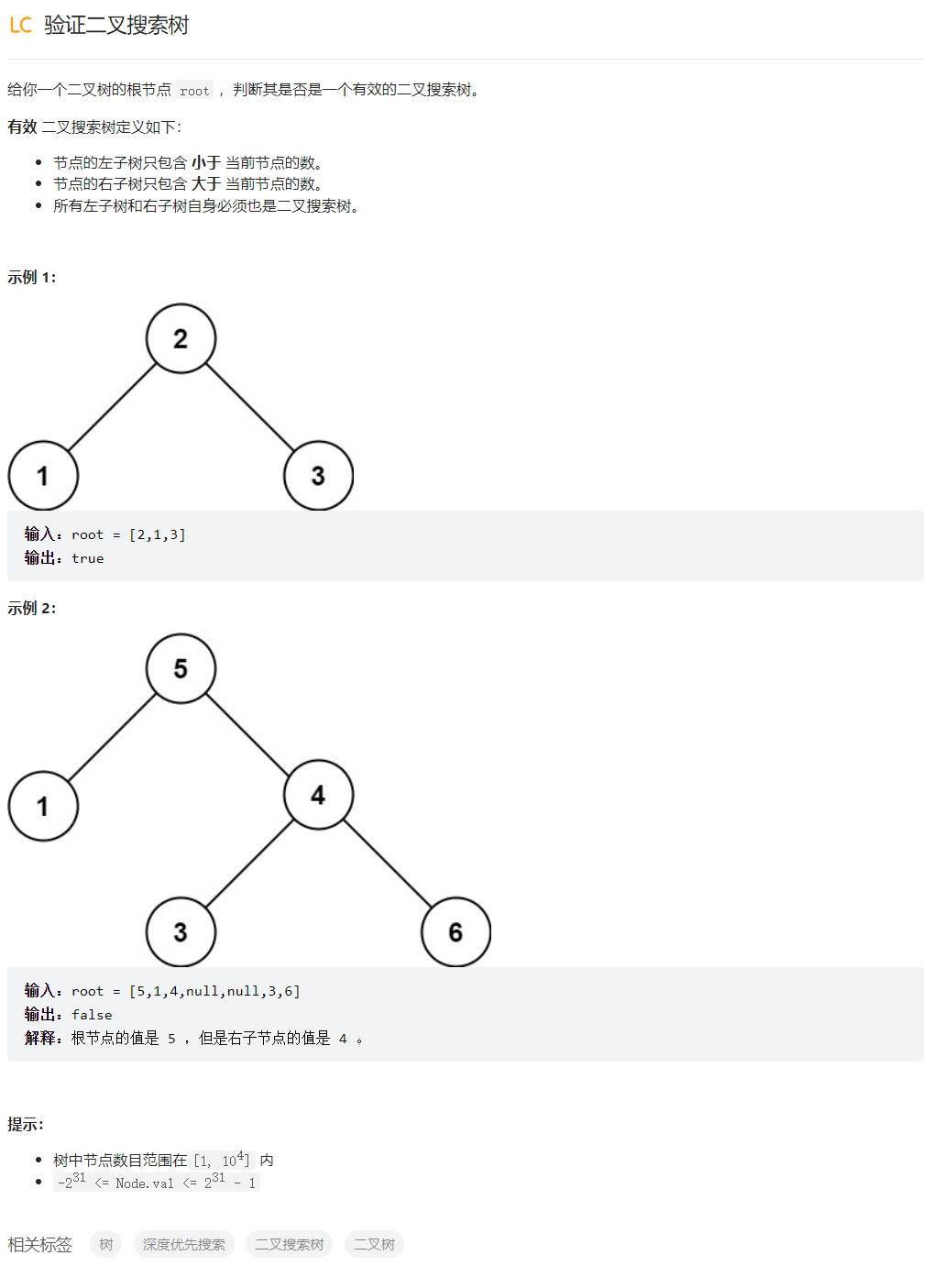
验证二叉搜索树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode *root,long minVal,long maxVal){
        if(root==NULL)
            return true;
        if(root->val<=minVal || root->val>=maxVal)
            return false;
        return isValidBST(root->left,minVal,root->val) && isValidBST(root->right,root->val,maxVal);
    }
    bool isValidBST(TreeNode* root) {
        return isValidBST(root,LONG_MIN,LONG_MAX);
    }
};

解题思路

做这题之前我们首先要明白什么是二叉搜索树，就是每个节点左子树的值都比当前节点小，右子树的值都比当前节点大。所以看到这里我们最先想到的就是递归，我最先想到的是下面这种写法（注意是错误的）

public boolean isValidBST(TreeNode root) {
    if (root == null)
        return true;
    if (root.left != null && root.val <= root.left.val || root.right != null && root.val >= root.right.val)
        return false;
    return isValidBST(root.left) && isValidBST(root.right);
}

如果一个结点是空的，我们默认他是有效的二叉搜索树。

否则如果左节点不为空，我们要判断是否大于左节点的值。

如果右节点不为空，我们还要判断小于右节点的值。

然后我们再以左右两个子节点用相同的方式判断。看起来好像没什么问题，但我们好像忽略了一个每个节点的上限和下限，比如下面这棵树

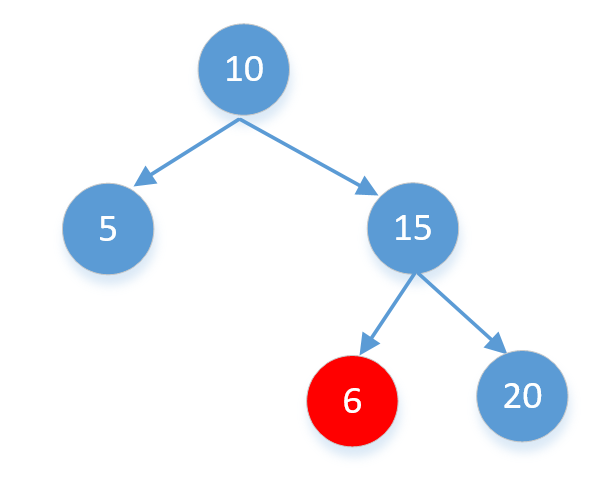
注意6这个节点不光要小于15而且还要大于10，所以这里的每一个节点都是有一个范围的，上面的代码我只判断了6比15小，但没有和10进行比较，所以代码是错误的。这里我们来给每个节点添加一个范围，如果不在这个范围之内直接返回false，比如6的范围是(10,15)，很明显他不在这个范围内，所以他不是二叉搜索树。根节点的范围我们从Long.MIN_VALUE到Long.MAX_VALUE。

对称二叉树

/**
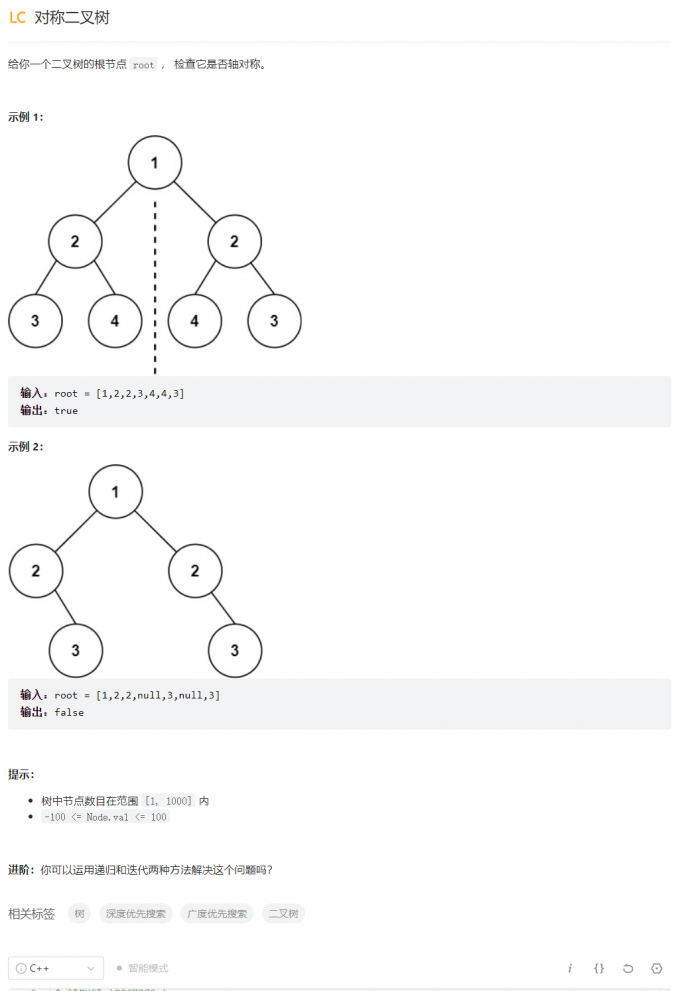
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetricHelper(TreeNode *left, TreeNode *right){
        //如果left和right都是NULL则直接返回true
        if(left==NULL && right==NULL)
            return true;
        //如果left或right其中一个为NULL或者left的值与right的值不等则直接返回false
        if(left==NULL || right==NULL || left->val!=right->val)
            return false;
        return isSymmetricHelper(left->left,right->right) && isSymmetricHelper(left->right,right->left);
    }
    bool isSymmetric(TreeNode* root) {
        return isSymmetricHelper(root->left,root->right);
    }
};

二叉树的层序遍历

/**
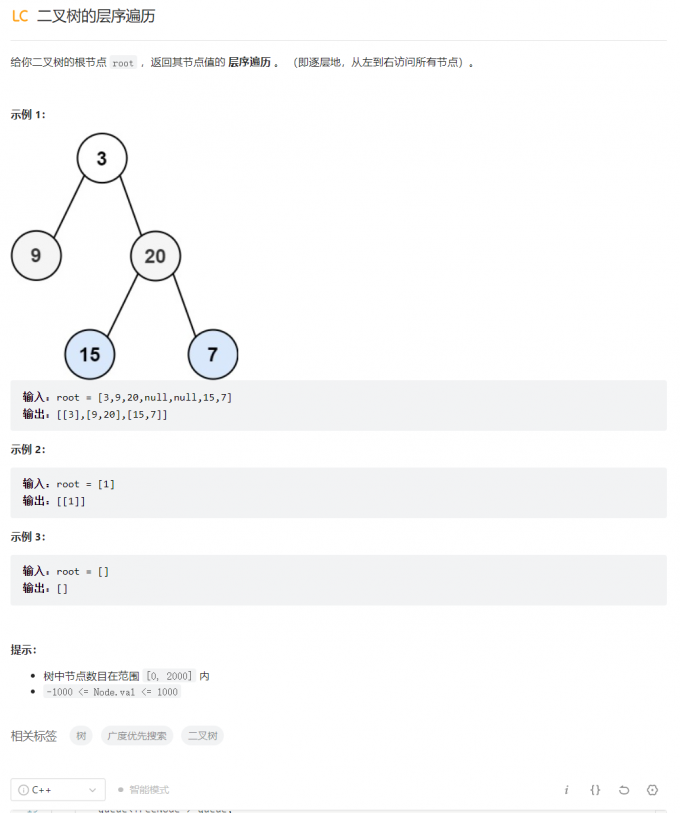
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        if(root==NULL){
            return result;
        }
        queue<TreeNode*> queue;
        queue.push(root);
        while (!queue.empty()){
            vector<int> row;
            int num=queue.size();
            for(int i=0;i<num;i++){
                TreeNode *node=queue.front();
                row.push_back(node->val);
                if(node->left!= nullptr){
                    queue.push(node->left);
                }
                if(node->right!= nullptr){
                    queue.push(node->right);
                }
                queue.pop();
            }
            result.push_back(row);
        }
        return result;
    }
};

将有序数组转换为二叉搜索树

/**
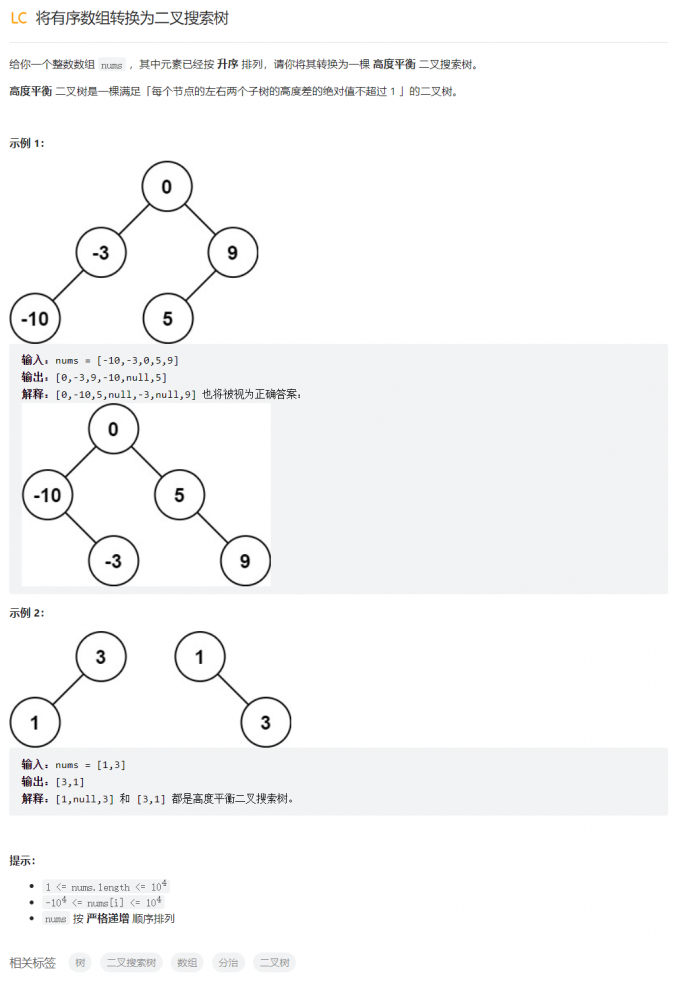
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums,int start,int end){
        if(start>end){
            return nullptr;
        }
        int mid=(start+end)>>1;
        TreeNode *root=new TreeNode(nums[mid]);
        root->left=sortedArrayToBST(nums,start,mid-1);
        root->right=sortedArrayToBST(nums,mid+1,end);
        return root;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return sortedArrayToBST(nums,0,nums.size()-1);
    }
};

解题思路

题中说了要转换为一棵高度平衡的二叉搜索树，并且数组又是排过序的，这就好办了，我们可以使用递归的方式，每次取数组中间的值比如m作为当前节点，m前面的值作为他左子树的结点值，m后面的值作为他右子树的节点值，示例中一个可能的结果是

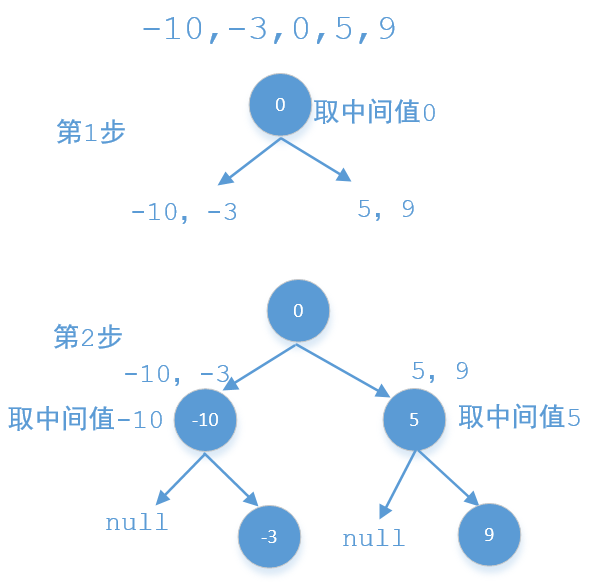
合并两个有序数组

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int p1=0,p2=0;//定义双指针
        while(p1<m && p2<n){
            if(nums2[p2]<nums1[p1]){
                //如果p2指针指向的值小于p1指向的值，则p1后面的值全部向右移动一位
                for(int i=m-1;i>=p1;i--){
                    nums1[i+1]=nums1[i];
                }
                //将p2指向的值插入到p1指向的位置
                nums1[p1]=nums2[p2];
                //m表示当前nums1数组的长度
                m++;
                //p2指针向右移动一位
                p2++;
            }
            //p1指针向右移动一位
            p1++;
        }
        //如果p2指针没有指向nums2的末尾，则将其剩余的值添加到p1指针的后面
        if(p2<n){
            for(int i=p1;i<nums1.size();i++){
                nums1[i]=nums2[p2];
                p2++;
            }
        }
    }
};

第一个错误的版本

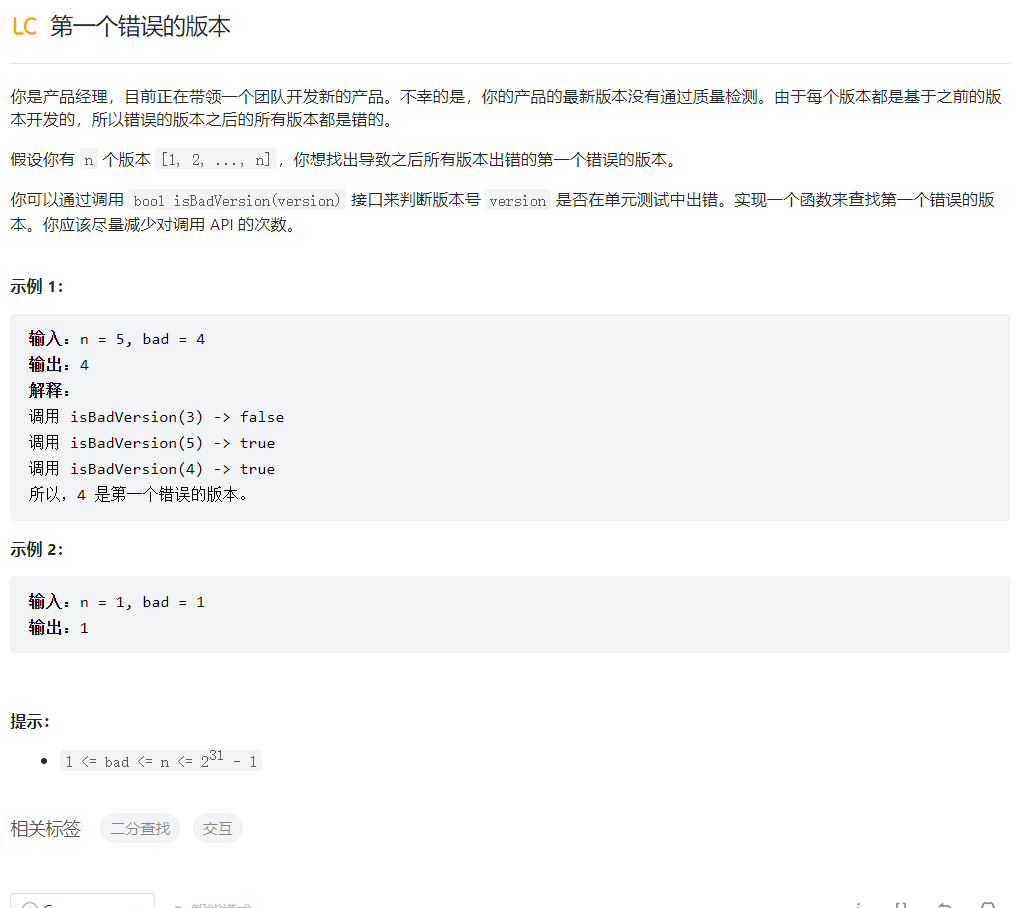
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        int start=1,end=n;
        int minBad=n;
        while(start<=end){
            //使用 mid=(start+end)/2 会超出int范围，所以使用这种去中间值的方法
            int mid=start+(end-start)/2;
            bool isBad=isBadVersion(mid);
            if(isBad){
                minBad=min(minBad,mid);
                end=mid-1;
            }
            else {
                start=mid+1;
            }
        }
        return minBad;
    }
};

爬楼梯

class Solution {
public:
    //n阶楼梯的方法数与斐波那契数列相对应，所以本题只需要构建一个斐波那契数列即可
    int climbStairs(int n) {
        if(n<4){
            return n;
        }
        int *arr=new int[n+1]{0};
        arr[1]=1;
        arr[2]=2;
        for(int i=3;i<n+1;i++){
            arr[i]=arr[i-1]+arr[i-2];
        }
        return arr[n];
    }
};

买卖股票的最佳时机

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int p1=0,p2=1;
        int maxProfit=0;
        while(p2<prices.size()){
            if(prices[p2]<prices[p1]){
                p1=p2;
            }
            if(prices[p2]-prices[p1]>maxProfit){
                maxProfit=prices[p2]-prices[p1];
            }
            p2++;
        }
        return maxProfit;
    }
};

解题思路

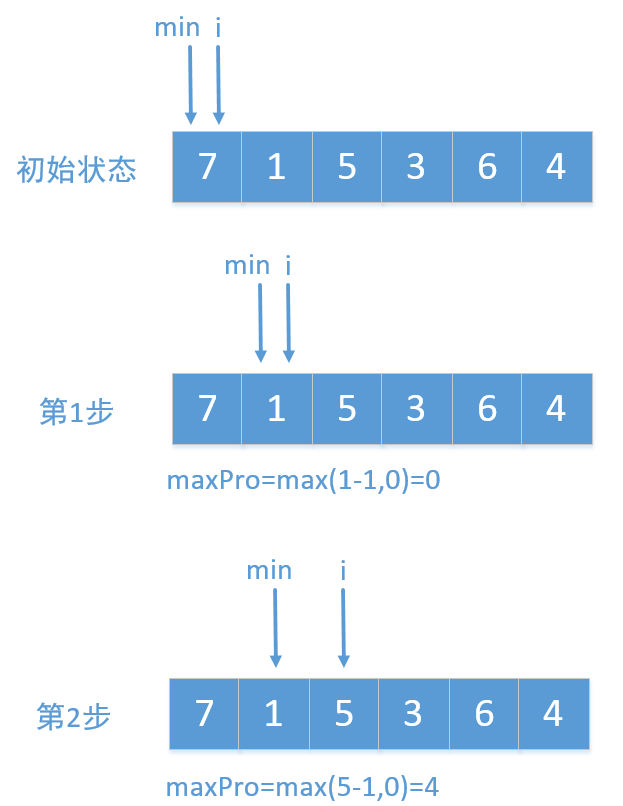
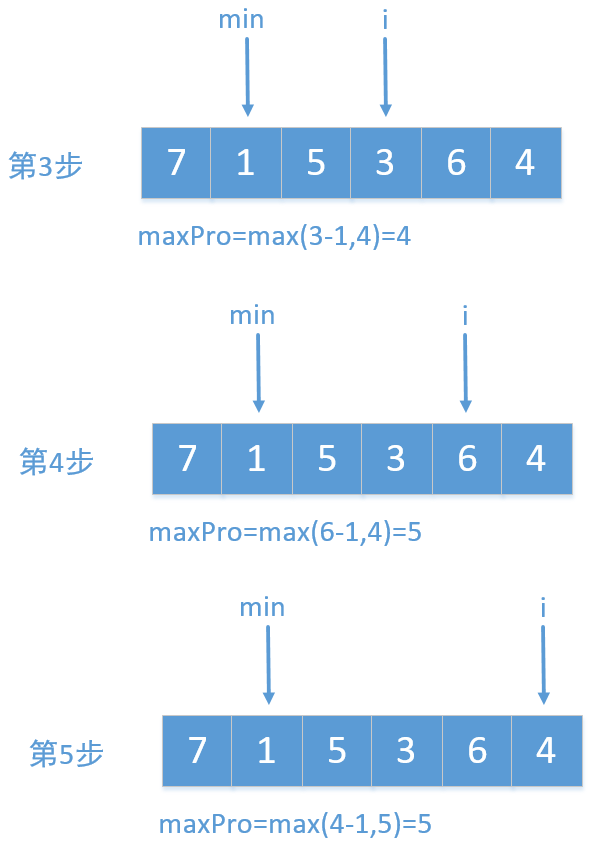
我们还可以使用两个指针，一个指针记录访问过的最小值（注意这里是访问过的最小值），一个指针一直往后走，然后计算他们的差值，保存最大的即可，这里就以示例1为例来画个图看下

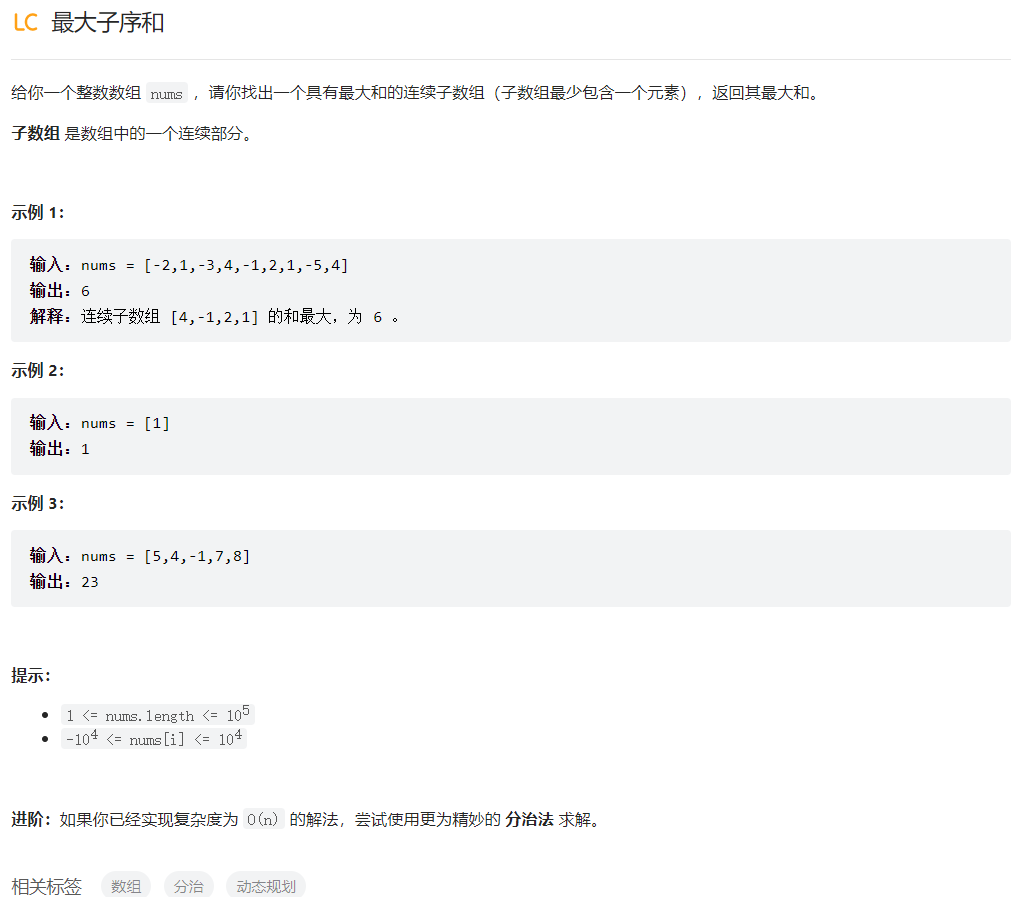
最大子序和

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int cur=nums[0];
        int max=cur;
        for(int i=1;i<nums.size();i++){
            cur=std::max(cur,0)+nums[i];
            max=std::max(max,cur);
        }
        return max;
    }
};

解题思路

1，动态规划解决
这题是让求最大的连续子序和，如果不是连续的非常简单，只需要把所有的正数相加即可。但这里说的是连续的，中间可能掺杂负数，如果求出一个最大子序和在加上负数肯定要比原来小了。解这题最简单的一种方式就是使用动态规划。

我们先来了解一下动态规划的几个步骤

1，确定状态

2，找到转移公式

3，确定初始条件以及边界条件

4，计算结果。

最后一个不用看，只看前3个就行，因为前3个一旦确定，最后一个结果也就出来了。我们试着找一下

1，定义dp[i]表示数组中前i+1（注意这里的i是从0开始的）个元素构成的连续子数组的最大和。

2，如果要计算前i+1个元素构成的连续子数组的最大和，也就是计算dp[i]，只需要判断dp[i-1]是大于0还是小于0。如果dp[i-1]大于0，就继续累加，dp[i]=dp[i-1]+num[i]。如果dp[i-1]小于0，我们直接把前面的舍弃，也就是说重新开始计算，否则会越加越小的，直接让dp[i]=num[i]。所以转移公式如下

dp[i]=num[i]+max(dp[i-1],0);

3，边界条件判断，当i等于0的时候，也就是前1个元素，他能构成的最大和也就是他自己，所以

dp[0]=num[0];

打家劫舍

class Solution {
public:
    int rob(vector<int>& nums) {
        int noSteal=0;//没偷第一家
        int steal=nums[0];//偷了第一家
        for(int i=1;i<nums.size();i++){
            int temp=std::max(noSteal,steal);
            //将上一家没偷和偷了的值进行比较，取较大值
            //max(noSteal,steal)表示当前这一家没有偷，则上一家偷没偷都可以，取较大值
            //noSteal+nums[i]表示当前这一家被偷了，则上一家必定没有被偷
            steal=noSteal+nums[i];
            noSteal=temp;
        }
        return max(noSteal,steal);
    }
};

1，动态规划解决

数组中的值表示的是存放的金额，小偷可以选择偷和不偷，如果前一个偷了，那么下一个肯定是不能偷的，因为相邻的房屋在同一晚上被小偷闯入，系统会自动报警。如果上一个没偷，那么下一个可以选择偷也可以选择不偷，视情况而定。

这里可以定义一个二维数组dp[length][2]，其中dp[i][0]表示第i+1（因为数组下标是从0开始的，所以这里是i+1）家偷了的最大总金额，dp[i][1]表示的是第i+1家没偷的最大总金额。那么我们找出递推公式

1，dp[i][0]=max(dp[i-1][0],dp[i-1][1])

他表示如果第i+1家没偷，那么第i家有没有偷都是可以的，我们取最大值即可。

2，dp[i][1]=dp[i-1][0]+nums[i]

他表示的是如果第i+1家偷了，那么第i家必须没偷，这里nums[i]表示的是第i+1家偷的金额。

递推公式找出来之后我们再来看下边界条件，第一家可以选择偷，也可以选择不偷，所以

dp[0][0]=0，第一家没偷

dp[0][1]=nums[0]，第一家偷了

打乱数组

class Solution {
private:
    vector<int> v;
public:
    Solution(vector<int>& nums) {
        v=nums;
    }

    vector<int> reset() {
        return v;
    }
    
    vector<int> shuffle() {
        int size=v.size();
        vector<int> arr(v);
        for(int i=1;i<size;i++){
            swap(arr[i],arr[rand()%(i+1)]);
        }
        return arr;
    }
};

/**
 * Your Solution object will be instantiated and called as such:
 * Solution* obj = new Solution(nums);
 * vector<int> param_1 = obj->reset();
 * vector<int> param_2 = obj->shuffle();
 */

最小栈

class MinStack {
private:
    stack<long> stack;
    vector<long> minValue;
    int index;
public:
    MinStack() {
        index=0;
    }
    
    void push(long val) {
        if(index==0){
            minValue.push_back(val);
        }
        else{
            minValue.push_back(min(val,minValue[index-1]));
        }
        index++;
        stack.push(val);
    }
    
    void pop() {
        index--;
        minValue.pop_back();
        stack.pop();
    }
    
    int top() {
        return stack.top();
    }
    
    int getMin() {
        return minValue[index-1];
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */

Fizz Buzz

class Solution {
public:
    vector<string> fizzBuzz(int n) {
        vector<string> res;
        for(int i=1;i<=n;i++){
            if(i%15==0){
                res.push_back("FizzBuzz");
            }
            else if(i%3==0){
                res.push_back("Fizz");
            }
            else if(i%5==0){
                res.push_back("Buzz");
            }
            else {
                res.push_back(to_string(i));
            }
        }
        return res;
    }
};

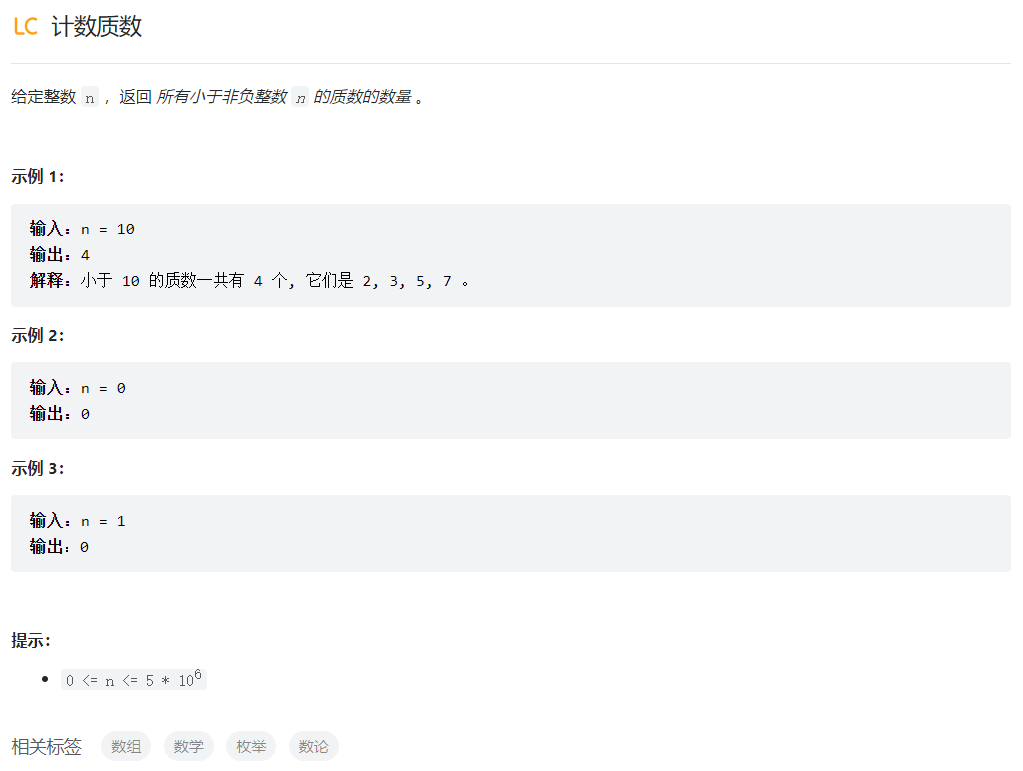
计数质数

class Solution {
public:
    int countPrimes(int n) {
        int count=0;
        vector<bool> isPrime(n,true);
        for(int i=2;i<n;i++){
            if(isPrime[i-1]){
                count++;
                for(int j=i*2;j<n;j+=i){
                    isPrime[j-1]=false;
                }
            }
        }
        return count;
    }
};

解题思路

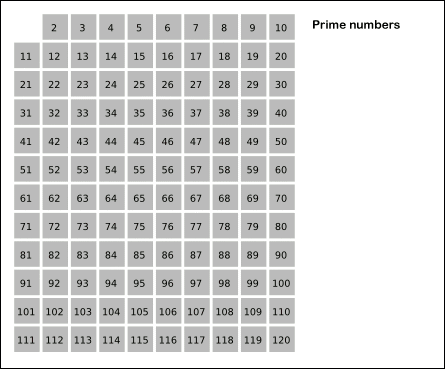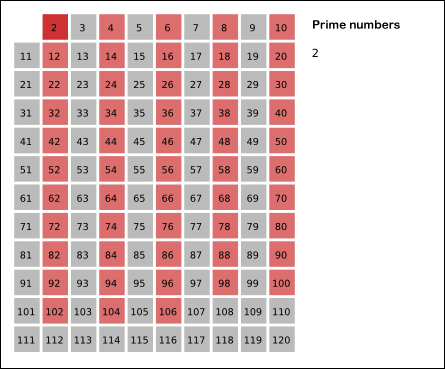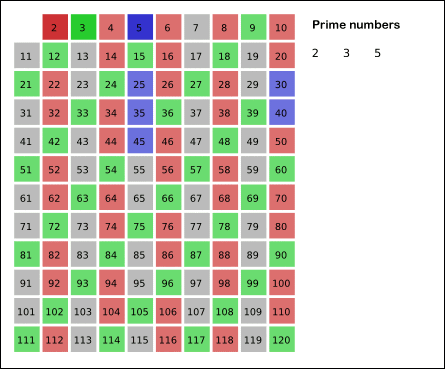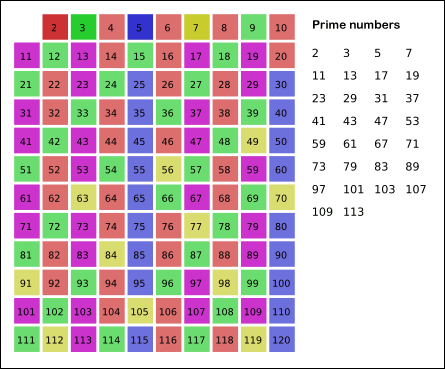
首先，将2到n范围内的所有整数写下来。其中最小的数字2是素数。将表中所有2的倍数都划去。表中剩余的最小数字是3，它不能被更小的数整除，所以是素数。再将表中所有3的倍数全都划去。依次类推，如果表中剩余的最小数字是m时，m就是素数。然后将表中所有m的倍数全部划去。像这样反复操作，就能依次枚举n以内的素数。

3的幂

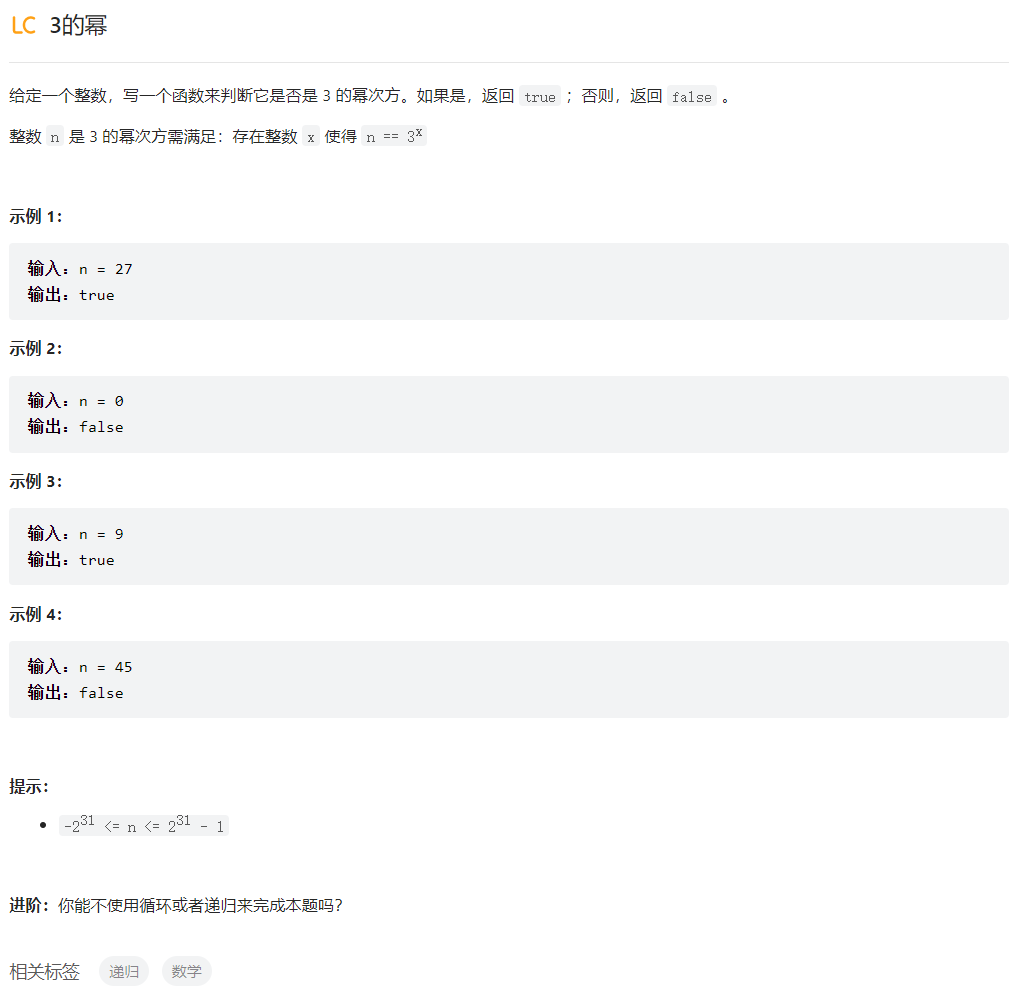
class Solution {
public:
    bool isPowerOfThree(int n) {
        return n>0 && (n==1 || (n%3==0 && isPowerOfThree(n/3)));
        /*题中n的范围是-2^31 <= n <= 2^31 - 1，而在这个范围内3的最大幂是1162261467，在比他大就超过int表示的范围了，我们直接用它对n求余即可，过求余的结果是0，说明n是3的幂次方*/
        //return n>0 && 1162261467%n==0;
    }
};

罗马数字转整数

class Solution {
public:
    int getValue(char c){
        switch (c) {
            case 'I':
                return 1;
            case 'V':
                return 5;
            case 'X':
                return 10;
            case 'L':
                return 50;
            case 'C':
                return 100;
            case 'D':
                return 500;
            case 'M':
                return 1000;
            default:
                return 0;
        }
    }
    int romanToInt(string s) {
        int preVal=getValue(s[0]);
        int res=0;
        for(int i=1;i<s.length();i++){
            int val=getValue(s[i]);
            if(preVal<val){
                res-=preVal;
            }
            else {
                res+=preVal;
            }
            preVal=val;
        }
        res+=preVal;
        return res;
    }
};

通常情况下，罗马数字中小的数字在大的数字的右边。也就是说如果小写的在大写的右边，每个字符都是一个有效的数字，他表示的数字就是所有字符相加，比如VI就是5+1=6。

如果小写的在大写的左边，就是无效的，只有一种情况，就是这个小写的和大写的组成一个数字，比如IV表示的是5-1=4。

位1的个数

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count=0;
        while(n!=0){
            if(n%2!=0){
                count++;
            }
            n=n>>1;
        }
        return count;
    }
};

汉明距离

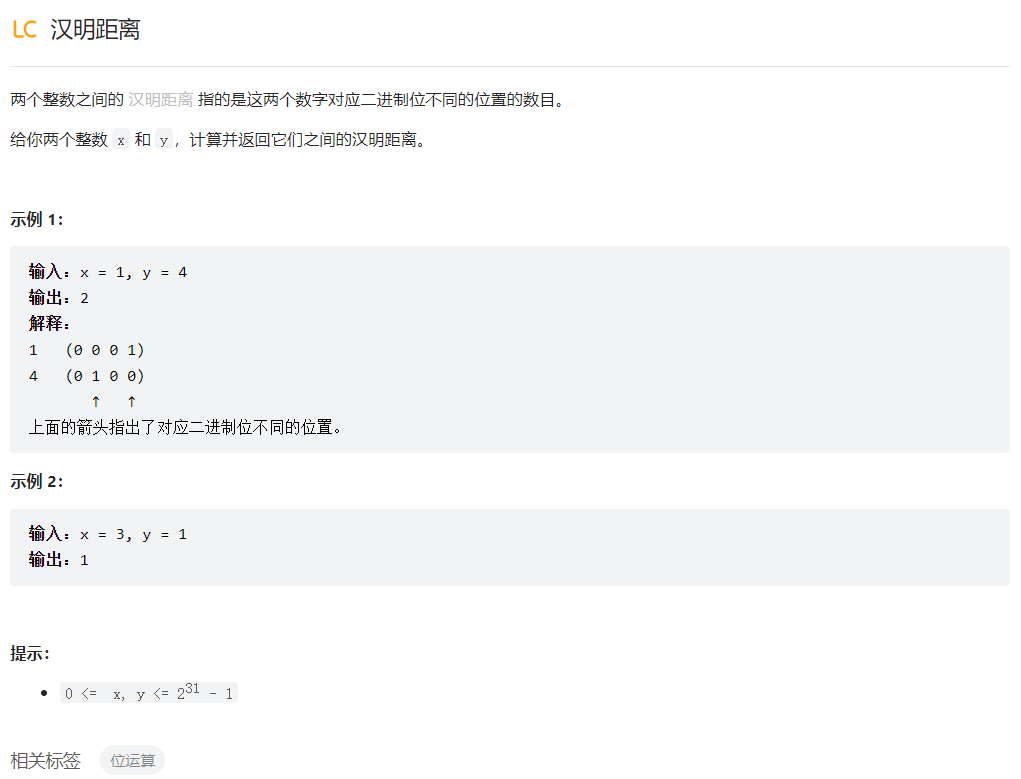
class Solution {
public:
    int hammingDistance(int x, int y) {
        int temp=x^y;
        int distance=0;
        while(temp!=0){
            if(temp%2!=0){
                distance++;
            }
            temp>>=1;
        }
        return distance;
    }
};

颠倒二进制位

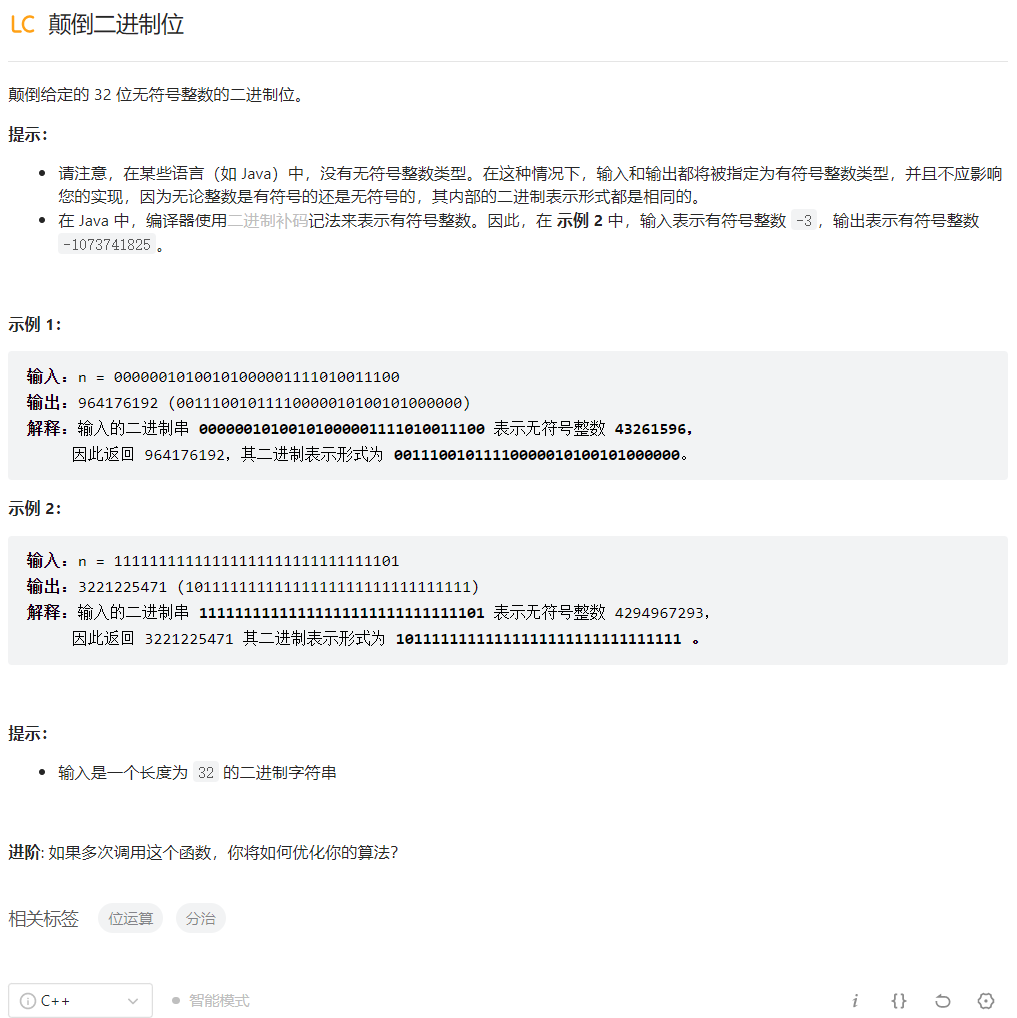
class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        int res=0;
        for(int i=0;i<32;i++){
            int end=n%2;
            res<<=1;
            res|=end;
            n/=2;
        }
        return res;
    }
};

杨辉三角

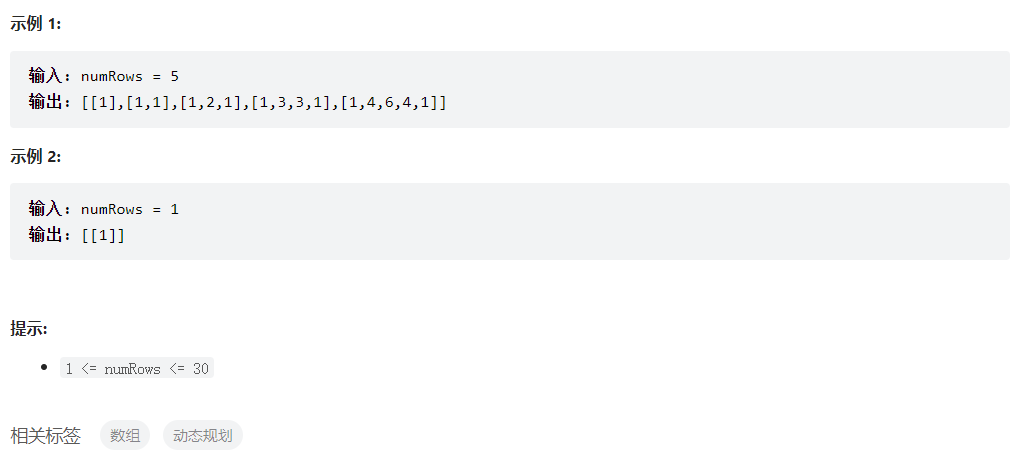
class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> res;
        for(int i=0;i<numRows;i++){
            vector<int> row;
            for(int j=0;j<=i;j++){
                if(j==0 || i==j){
                    row.push_back(1);
                }
                else{
                    row.push_back(res[i-1][j-1]+res[i-1][j]);
                }
            }
            res.push_back(row);
        }
        return res;
    }
};

有效的括号

class Solution {
public:
    bool isValid(string s) {
        stack<char> stack;
        for(char c:s){
            if(c=='(' || c=='[' || c=='{'){
                stack.push(c);
            }
            else {
                if(stack.empty()){
                    return false;
                }
                char temp=stack.top();
                if(!((c==')' && (c-1)==temp) || ((c-2)==temp))){
                    return false;
                }
                stack.pop();
            }
        }
        return stack.empty();
    }
};

缺失数字

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int res=0;
        for(int i=0;i<nums.size();i++){
            res^=nums[i]^i;
        }
        return res^nums.size();
    }
};

解题思路

将这题转换思路，改成仅仅出现一次的数字是谁

比如原先数字是0，1，3 那么我为他补上0，1，2，3那么2就是仅出现一次的数字

使用异或运算，将所有值进行异或

异或运算，相异为真，相同为假，所以 a^a = 0 ;0^a = a

因为异或运算 满足交换律 a^b^a = a^a^b = b 所以数组经过异或运算，单独的值就剩下了

请参考下面的例题：只出现一次的数字