归并排序
归并排序
本文分为以下几个部分
问题引入
求一串非空数组中的最大值,使用O(n)的时间复杂度。
最直接想到的代码就是直接一次遍历
@Test
public void maxNum1(){
int arr[] = {2, 3, 4, 1, 54, 1, 0};
int max = arr[0];
for(int i = 1; i < arr.length; i++){
max = Math.max(max,arr[i]);
}
System.out.println(max);
}
另一种不容易想到的是递归
@Test
public void maxNum2(){
int[] arr = {2, 3, 4, 1, 54, 1, 0};
System.out.println(getMax(arr, 0, arr.length - 1));
}
private int getMax(int[] arr,int L,int R){
if(L == R){
return arr[L];
}
//取中点值,直接使用 (R+L)/2 可能会越界
//L+(R-L)/2 ,除2等同于位运算右移一位,位运算相对除法较快
int mid = L + ((R-L)>>1);
int M1 = getMax(arr,L,mid);
int M2 = getMax(arr,mid+1,R);
return Math.max(M1,M2);
}
代码流程如下
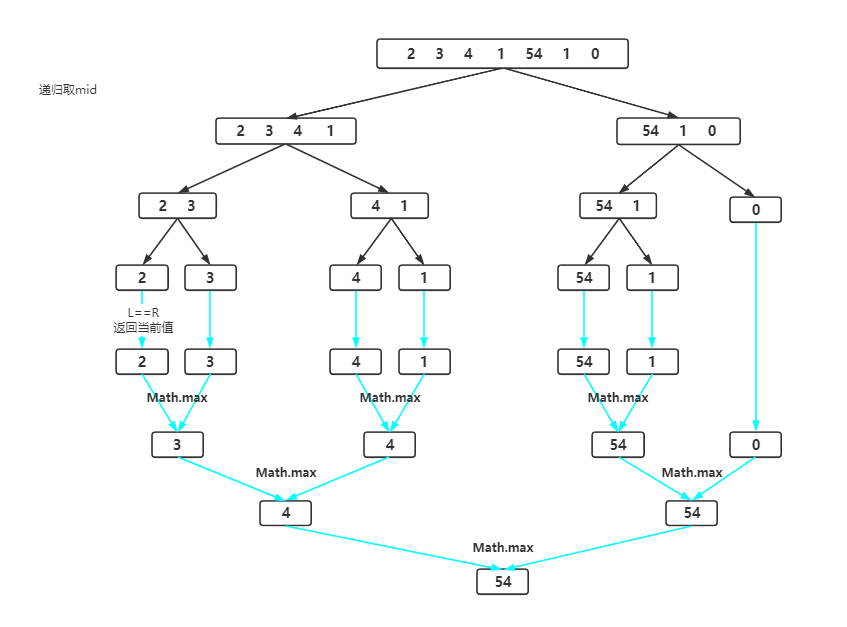
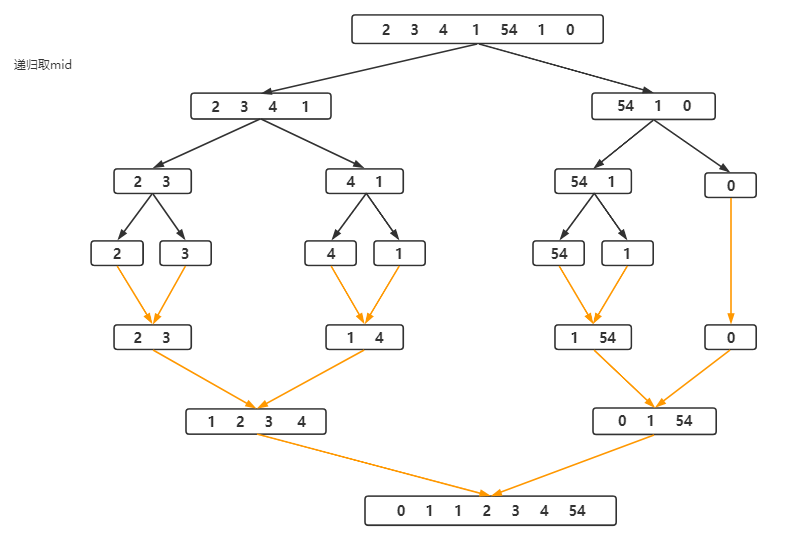
将数据两两分,然后再细分,分到最后,会到 L == R,然后 return 回去,右递归或者比较左右两遍的数,return 较大的数。
用到了递归,怎么说他的时间复杂度是 O(n) 呢?
使用Mater公式来计算!
Master 公式
直接上公式

时间复杂度计算

相当于上面一题,每次 getMax() 方法中递归调用了两次,所以 a 2,每次相对上次的数据规模为一半,所以 b = 2,除递归外其他的时间复杂度为 O(1),所以 d = 0
logb a = 1, d = 0,所以时间复杂度为 O(n),符合题意。
归并排序
类似上面的取大数的递归方法,多个数排序,可以看成两个数排序,然后越来越多的数排序。
取大数就是两个数比较,得出大数,然后继续和其他的比较,此时其实就是多个数在比较了。
和取大数的比较,不同点就在一个是取数,一个是排序,其他都相同。
排序方法
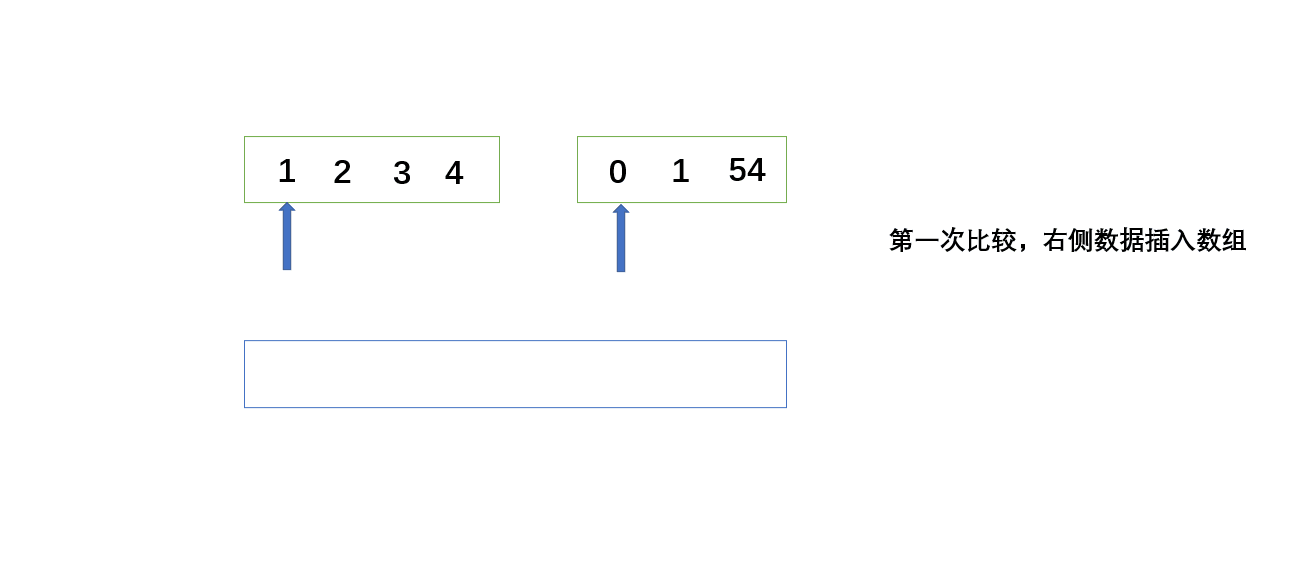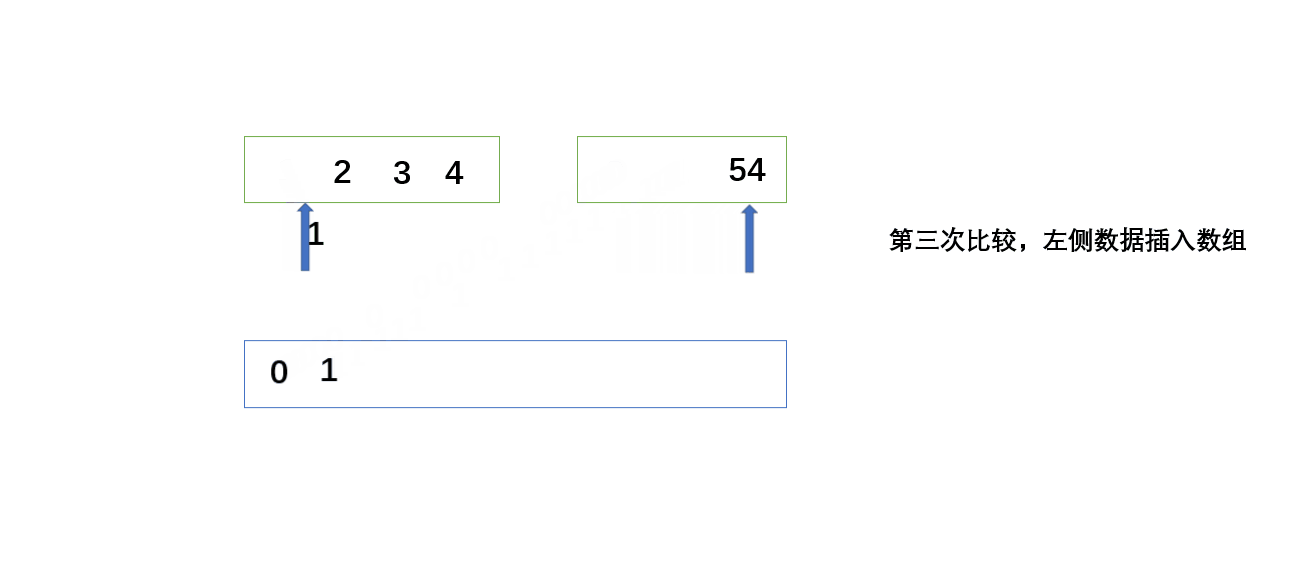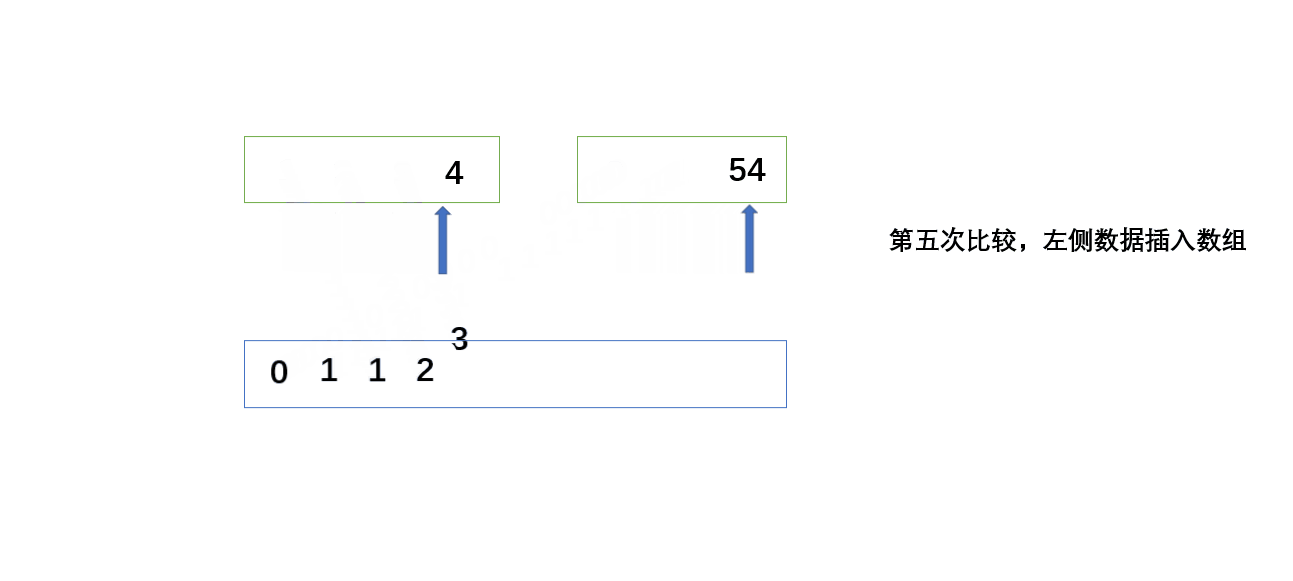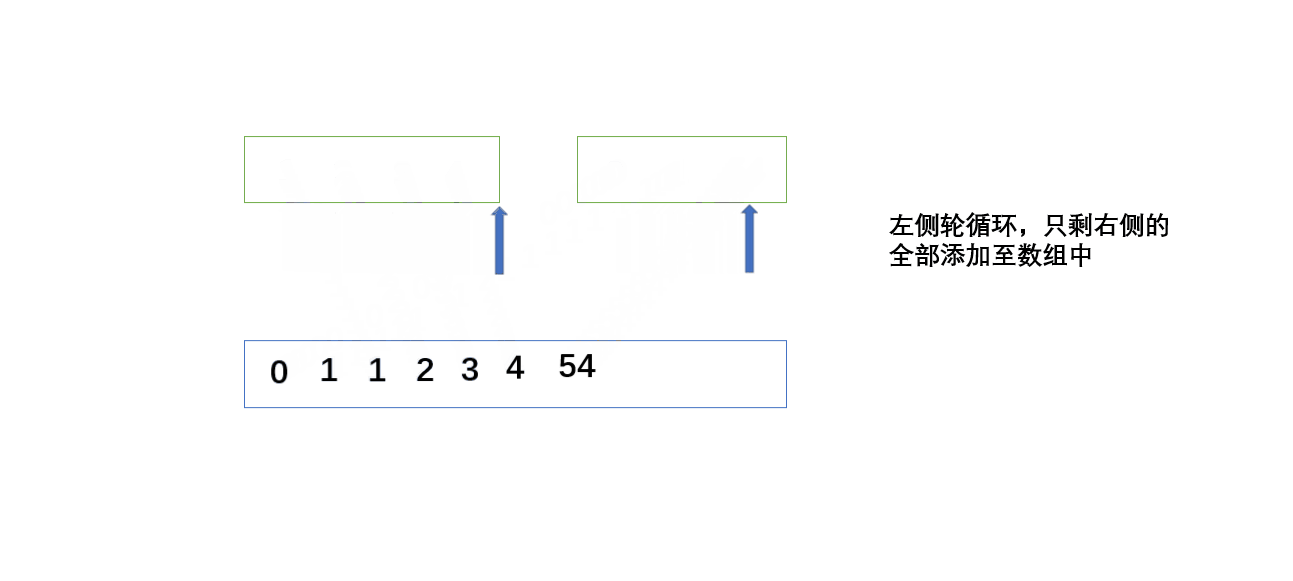
数组分成两个,同时两个指针从左到右依次遍历,新建一个数组,哪个数据小,就添加到新数组当中。
由于都是从数据量小开始,所以小数据会先排序,最后会成两个已经排好序的数组再进行排序。
@Test
public void sort(){
int arr[] = {2, 3, 4, 1, 54, 1, 0};
dfs(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
private void dfs(int[] arr,int L,int R){
if(L == R){
return;
}
int mid = L + ((R-L)>>1);
dfs(arr,L,mid);
dfs(arr,mid+1,R);
mergeSort(arr,L,mid,R);
}
private void mergeSort(int[] arr,int L,int mid,int R){
int[] copy = new int[R-L+1];
int RStart = mid + 1;
int LStart = L;
int copyStart = 0;
while (LStart <= mid && RStart <= R){
copy[copyStart++] = arr[LStart] < arr[RStart] ? arr[LStart++] : arr[RStart++];
}
while (LStart <= mid){
copy[copyStart++] = arr[LStart++];
}
while (RStart <= R){
copy[copyStart++] = arr[RStart++];
}
for(int i = 0; i < copy.length; i++){
arr[L+i] = copy[i];
}
}
时间复杂度计算
使用 master 公式
a = 2; b = 2; 除递归的时间复杂度为 O(n),就是遍历两遍 L-R 的数组,所以时间复杂度为 O(n),所以 d = 1
logb a = 1, d = 1,符合第二个
所以递归时间复杂度为 O(n log n) (计算机中通常log都定义为以2为底的数,log2)
写在最后
看上面 gif 图 理解就行,剩下递归理解第一个问题就行。


