二叉树的遍历(BFS、DFS)
二叉树的遍历(BFS、DFS)
本文分为以下部分:
BFS(广度优先搜索)
广度优先搜索[^1](英语:Breadth-First Search,缩写为BFS),又译作宽度优先搜索,或横向优先搜索,是一种图形搜索算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。广度优先搜索的实现一般采用open-closed表。
先遍历每层的节点,优先对相邻节点做相同操作,再对下一层进行操作,直到所有操作完成。
简单来说就是一层一层的进行操作,横向操作。
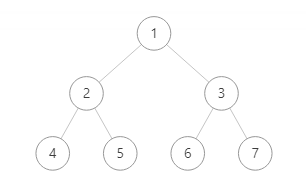
例如上图,用广度优先搜索算法将节点值输出,则输出结果为 1 2 3 4 5 6 7
第一层输出 1 ,然后输出第二层 2 3 ,最后输出第三层 4 5 6 7
实现方法:
(队列先进先出原则)
-
首先定义一个单端队列,将根节点加入队列中
-
判断队列是否为空,不为空则取出队列的第一个节点,输出节点的值,将节点的左、右节点加入队列中
-
重复第二步,直到队列为空
e.g.
- 定义一个单端队列queue,将根节点 1 加入队列中
- 从队列中取出节点 1 ,输出节点的的值 1 ,将节点 2 、3 加入队列中
- 由于队列先进先出特性,所以取出节点 2 , 输出节点值 2 ,将节点 4 、5 加入队列
- 此时取出的是节点 3,输出节点值 3 ,将节点 6 、7 加入队列
- ......
最终输出为 1 2 3 4 5 6 7
public class ErgodicTree {
@Test
public void test(){
Node root = new Node(1);
Node node = new Node(2);
Node node1 = new Node(3);
Node node2 = new Node(4);
Node node3 = new Node(5);
Node node4 = new Node(6);
Node node5 = new Node(7);
root.setLeft(node);
root.setRight(node1);
node.setLeft(node2);
node.setRight(node3);
node1.setLeft(node4);
node1.setRight(node5);
this.bfs(root);
}
//广度优先搜索
//1 => 2 => 3 => 4 => 5 => 6 => 7 =>
public void bfs(Node node){
Queue<Node> queue = new LinkedList<Node>();
//将根节点加入队列中
queue.offer(node);
while (!queue.isEmpty()){
//获取队列的第一个节点
Node poll = queue.poll();
if(poll != null){
//输出获取到的节点值
System.out.print(poll.getValue() + " => ");
//将该节点的左侧节点加入队列中
queue.offer(poll.getLeft());
//将该节点的右侧节点加入队列中
queue.offer(poll.getRight());
}
}
}
}
//节点定义
class Node{
private int value;
private Node left;
private Node right;
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
DFS(深度优先搜索)
深度优先搜索算法[^1](英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。这个算法会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
遍历一列的节点,再对下一列的节点进行操作,直到所有操作完成
简单来说就是一列一列的进行操作,纵向操作。
先序遍历
(先)根左右
每次遍历都先根,再遍历左子树,再遍历右子树,依旧以上图为例

- 先根节点,输出 1
- 再遍历左子树,左子树为 2 4 5
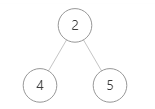
- 遍历左子树的根节点,输出 2
- 再遍历左子树,左子树为单独的 4 ,所以输出 4
- 2 的左子树遍历完,再遍历 2 的右子树,右子树为单独的 5 ,所以输出 5
- 1 的左子树遍历完,回溯遍历 1 的右子树,右子树为 3 6 7

- 遍历右子树依旧为先 根左右 ,根为 3 ,输出 3
- 再遍历左子树,左子树为单独的6,所以输出 6
- 3 的左子树遍历完,再遍历 3 的右子树,右子树为单独的 7 ,所以输出 7
整个树遍历完了,所以最终输出的是 1 2 4 5 3 6 7
代码实现
public class ErgodicTree {
@Test
public void test(){
Node root = new Node(1);
Node node = new Node(2);
Node node1 = new Node(3);
Node node2 = new Node(4);
Node node3 = new Node(5);
Node node4 = new Node(6);
Node node5 = new Node(7);
root.setLeft(node);
root.setRight(node1);
node.setLeft(node2);
node.setRight(node3);
node1.setLeft(node4);
node1.setRight(node5);
this.preOrder(root);
}
//先序遍历
//1 => 2 => 4 => 5 => 3 => 6 => 7 =>
public void preOrder(Node node){
if(node != null){
//输出当前节点
System.out.print(node.getValue() + " => ");
//遍历左子树
preOrder(node.getLeft());
//遍历右子树
preOrder(node.getRight());
}
}
}
class Node{
private int value;
private Node left;
private Node right;
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
中序遍历
(中)根左右,即 左根右
先序遍历是先根左右,中序遍历是中根左右,即左根右,左子树,根节点,再右子树,以最开始的图为例

- 先遍历根节点 1 的左子树 2 4 5

- 由于节点 2 还有左子树,所以先遍历 2 的左子树
- 左子树为单独的 4 ,4 没有左子树(若存在左子树,则需要继续往下递推),所以输出 4
- 2 的左子树遍历完,输出 2 的根节点自己,输出 2
- 2 的右子树依旧为 1 的左子树的部分,所以先遍历 2 的右子树
- 2右子树为单独的 5,5 没有左子树,所以输出 5
- 1 的左子树都遍历完了,该遍历 1 的根节点了,输出 1
- 再遍历 1 的右子树 3 6 7,右子树的遍历依旧遵循左根右

- 由于节点 3 还有左子树,所以先遍历 3 的左子树
- 左子树为单独的 6 ,6 没有他左子树,所以输出 6
- 3 的左子树遍历完,输出 3 的根节点自己,输出 3
- 接着遍历 3 的右子树
- 右子树为单独的 7,7 没有左子树,所以输出 7
最终输出为 4 2 5 1 6 3 7
代码实现
public class ErgodicTree {
@Test
public void test(){
Node root = new Node(1);
Node node = new Node(2);
Node node1 = new Node(3);
Node node2 = new Node(4);
Node node3 = new Node(5);
Node node4 = new Node(6);
Node node5 = new Node(7);
root.setLeft(node);
root.setRight(node1);
node.setLeft(node2);
node.setRight(node3);
node1.setLeft(node4);
node1.setRight(node5);
this.midOrder(root);
}
//中序遍历
//4 => 2 => 5 => 1 => 6 => 3 => 7 =>
public void midOrder(Node node){
if(node != null){
//先遍历左子树
midOrder(node.getLeft());
//输出当前节点
System.out.print(node.getValue() + " => ");
//遍历右子树
midOrder(node.getRight());
}
}
}
class Node{
private int value;
private Node left;
private Node right;
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
后序遍历
(后)根左右,即 左右根
后序遍历就是根在最后遍历,顺序为左右根,即左子树,右子树,根节点,依旧以最初的图为例

- 先遍历根节点 1 的左子树 2 4 5

- 由于节点 2 还有左子树,所以先遍历 2 的左子树
- 左子树为单独的 4 ,4 没有左子树,也没有右子树(若存在左/右子树,则需要继续往下递推),所以输出 4
- 遍历完 2 的左子树,再遍历 2 的右子树
- 右子树为单独的 5 ,5 没有左子树,也没有右子树,所以输出 5
- 最后遍历 2 自己,输出 2
- 再遍历根节点 1 的右子树

- 由于节点 3 还有左子树,所以先遍历 3 的左子树
- 左子树为单独的 6 ,6 没有左子树,也没有右子树,所以输出 6
- 遍历完 3 的左子树,再遍历 3 的右子树
- 左子树为单独的 7 ,7 没有左子树,也没有右子树,所以输出 7
- 最后遍历 3 自己,输出 3
- 最后遍历根节点 1 ,输出 1
最后的输出结果为 4 5 2 6 7 3 1
代码实现
public class ErgodicTree {
@Test
public void test(){
Node root = new Node(1);
Node node = new Node(2);
Node node1 = new Node(3);
Node node2 = new Node(4);
Node node3 = new Node(5);
Node node4 = new Node(6);
Node node5 = new Node(7);
root.setLeft(node);
root.setRight(node1);
node.setLeft(node2);
node.setRight(node3);
node1.setLeft(node4);
node1.setRight(node5);
this.postOrder(root);
}
//后序遍历
//4 => 5 => 2 => 6 => 7 => 3 => 1 =>
public void postOrder(Node node){
if(node != null){
postOrder(node.getLeft());
postOrder(node.getRight());
System.out.print(node.getValue() + " => ");
}
}
}
class Node{
private int value;
private Node left;
private Node right;
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
总结
-
BFS : 不用递归,使用队列来进行遍历操作。
-
DFS : 通常使用递归,三种遍历方式从代码上看就只是输出的位置的替换。
各有各的优点,不同问题不同分析。
参考文献
[^1]: 维基百科


 浙公网安备 33010602011771号
浙公网安备 33010602011771号